Δ.Ε.Π. : Μάθημα Φ1 : Θεμελιώδεις Αρχές και Εξέλιξη Φυσικής

Η σημερινή φυσική, βλέποντάς την από τη σκοπιά του 21^ου αιώνα, μπορούμε να πούμε οτι αποτελείται από δύο μεγάλες ενότητες:

Το παρόν μάθημα εξετάζει τις θεμελιώδεις αρχές και έννοιες της φυσικής, όπως αυτές εμφανίστηκαν αρχικά στην κλασική φυσική, και το πώς τροποποιήθηκαν (βελτιώθηκαν, συμπληρώθηκαν) αργότερα από τη μοντέρνα φυσική.

Θεμελιώδεις αρχές

Το πρόβλημα στη φυσική

Τί αναμένουμε από την εκφώνηση ενός προβλήματος φυσικής

Ας υποθέσουμε οτι έχουμε το κλασικό πρόβλημα του υπολογισμού της τροχιάς ενός βλήματος που εκτοξεύεται από ένα κανόνι (βλ. διάγραμμα, παρακάτω), με γνωστή αρχική ταχύτητα, γνωστή γωνία βολής, και πάνω στην επιφάνεια της Γης.

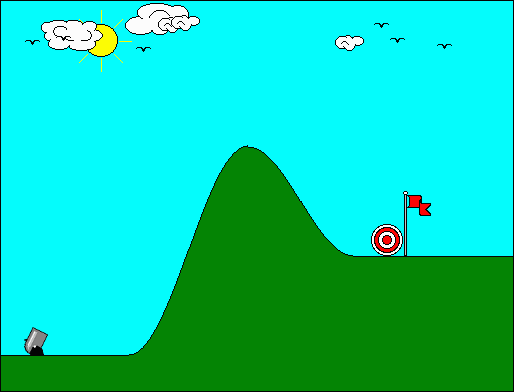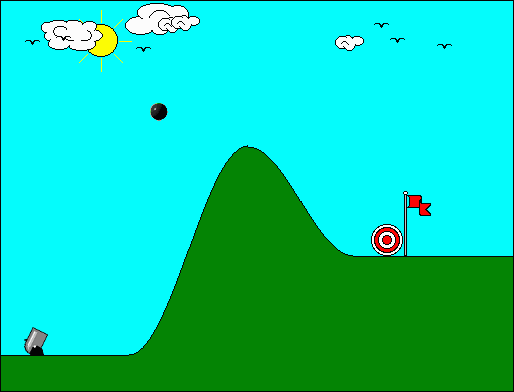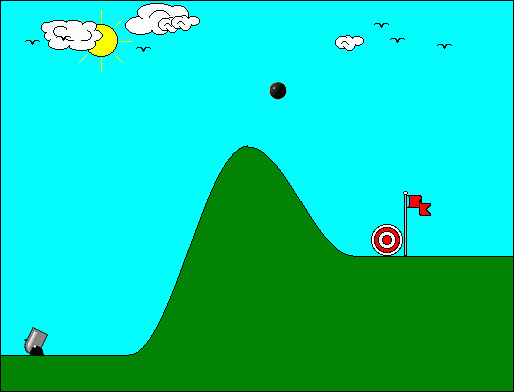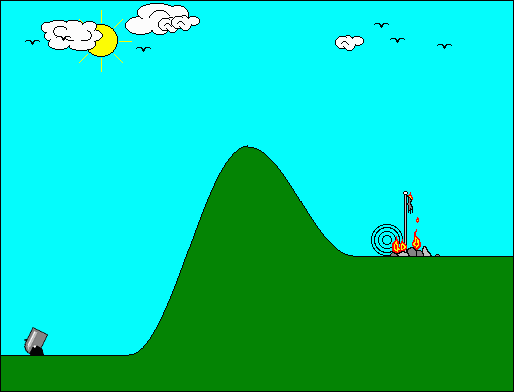
Τί υποθέσεις μπορούμε να κάνουμε για τη λύση αυτού του προβλήματος;

Αυτά που μπορούμε να υποθέσουμε — δεδομένου οτι το πρόβλημα έτσι όπως μας παρουσιάζεται έχει λύση — είναι τα εξής:

Τα πρώτα δύο από τα παραπάνω σημεία μπορούν να συνοψιστούν στο οτι η εκφώνηση του προβλήματος περιλαμβάνει τα “αναγκαία και ικανά” δεδομένα για τη λύση-του.

Το τρίτο σημείο, όσο κι αν φαίνεται προφανές, πρέπει να σημειώσουμε οτι αποτελεί μια “κατάκτηση” αυτού που ονομάζεται μερικές φορές “Δυτικός τρόπος σκέψης”. Παραδείγματα περιττών υποθέσεων ή ερωτημάτων που μπορεί ν’ απασχολήσουν κάποιον που δεν συμμερίζεται το Δυτικό τρόπο σκέψης είναι τα εξής:

Καμία από τις παραπάνω υποθέσεις δεν περιλαμβάνεται στην εκφώνηση, άρα πρόκειται για ερωτήματα άσχετα με το πρόβλημα. Για το τρίτο από τα παραπάνω ερωτήματα, το αν υπάρχει αντίσταση του αέρα ή όχι είναι ένα ζήτημα που αντιμετωπίζεται μεν σε τέτοιου είδους προβλήματα κλασικής φυσικής, αλλά εφόσον δεν αναφέρεται στην εκφώνηση, δεν πρέπει να το εισάγουμε από μόνοι-μας.

Απλοποιητικές υποθέσεις προκειμένου να γίνει ένας υπολογισμός

Έστω οτι ο παραπάνω υπολογισμός της τροχιάς του βλήματος δεν ζητείται σαν άσκηση ενός συγγράμματος, αλλά σαν πρόβλημα που παρουσιάζεται στην πράξη. Δηλαδή έχουμε μπροστά-μας ένα κανόνι, και ένα στόχο που πρέπει να πετύχουμε με το βλήμα. Έστω οτι δεν φυσάει αέρας, και φυσικά δεν υπάρχουν “εχθροί” που θα προσπαθήσουν να καταρρίψουν το βλήμα-μας — είναι μια ήσυχη μέρα και τίποτε το αναπάντεχο δεν πρόκειται να συμβεί. Προκειμένου λοιπόν να υπολογίσουμε πιο εύκολα το είδος της καμπύλης που θα ακολουθήσει το βλήμα, μπορούμε να κάνουμε τουλάχιστον δύο απλοποιητικές υποθέσεις:

Από τις δύο αυτές απλοποιητικές υποθέσεις έπεται οτι η τροχιά του βλήματος είναι παραβολική, όπως στο σχήμα:

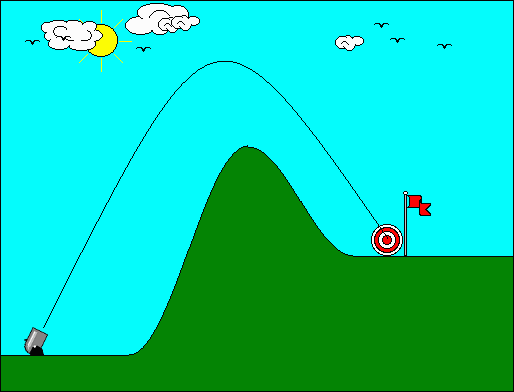
Η τροχιά είναι παραβολή όταν κάνουμε κάποιες απλοποιητικές υποθέσεις

Στην πραγματικότητα, καμία από τις παραπάνω δύο υποθέσεις δεν είναι σωστή. Πρώτο, η τιμή του g, που είναι ίση με 9,81 m/s² στην επιφάνεια της θάλασσας, ελαττώνεται όσο το βλήμα ανεβαίνει πιο ψηλά· και δεύτερο, η Γη φυσικά δεν είναι επίπεδη. Αν είχαμε να κάνουμε με βλήμα που φτάνει πολύ ψηλά σε σχέση με την ακτίνα της Γης, και που διανύει σημαντική απόσταση — πάλι σε σχέση με την ακτίνα της Γης — τότε θα είχαμε πιο σύνθετους υπολογισμούς, μέσω των οποίων η τροχιά του βλήματος θα έβγαινε ή ελλειπτική ή υπερβολική, ανάλογα με την αρχική ταχύτητα (βλ. σχήμα).

Η τροχιά μπορεί να είναι ελλειπτική (όπως στο σχήμα) ή υπερβολική
αν δεν κάνουμε τις παραπάνω δύο απλοποιητικές υποθέσεις

Σημαντικό όμως είναι να καταλάβουμε οτι η φυσική δίνει πρακτικές λύσεις σε προβλήματα. Το φυσικό δεν τον απασχολεί ιδιαίτερα αν το δέκατο ή δωδέκατο δεκαδικό ψηφίο ενός υπολογιζόμενου αριθμού θα βγει διαφορετικό αν χρησιμοποιηθεί πιο ακριβής μέθοδος (ή “φυσικό μοντέλο”· π.χ. το ένα μοντέλο θεωρεί τη Γη επίπεδη, ενώ το άλλο σαν σφαίρα). Αυτή είναι και μια διαφορά μεταξύ ενός φυσικού και ενός μαθηματικού. Ο μαθηματικός θα έλεγε οτι ούτε το μοντέλο που θεωρεί τη Γη σαν σφαίρα (και άρα την τροχιά σαν έλλειψη ή υπερβολή) είναι σωστό, γιατί κι αυτό το μοντέλο κάνει τις απλοποιητικές υποθέσεις οτι η μάζα της Γης είναι κατανεμημένη ομοιόμορφα, και οτι ισχύουν οι νόμοι του Kepler για την κίνηση των ουρανίων σωμάτων (άρα και για το βλήμα)· ενώ σύμφωνα με τη γενική θεωρία της γενικής σχετικότητας η τροχιά ενός σώματος που περιφέρεται γύρω από άλλο σώμα με πολύ μεγαλύτερη μάζα (όπως το βλήμα γύρω από τη Γη στο σχήμα) δεν είναι απλή έλλειψη, αλλά έλλειψη που περιστρέφεται (πολύ αργά) γύρω από τη μια εστία-της — όπως αποδείχτηκε μέσω παρατηρήσεων στην περίπτωση της τροχιάς του Ερμή, που το περιήλιό του μετατοπίζεται κατά 2° κάθε αιώνα (βλ. σχήμα).

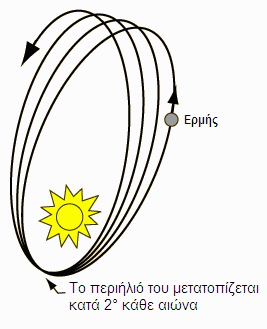
Όλα αυτά μας δείχνουν οτι ένα πρόβλημα που φαίνεται απλό, “στην πραγματικότητα” μπορεί να γίνει πολύ περίπλοκο αν επιμείνουμε να χρησιμοποιήσουμε το πιο ακριβές μοντέλο που γνωρίζουμε. Ο μαθηματικός δεν θα κατέληγε ποτέ σε μια απάντηση για το ερώτημα της τροχιάς του βλήματος γιατί θα έπρεπε να λύσει το — με αναλυτικές μεθόδους άλυτο — πρόβλημα της αμοιβαίας έλξης ν ουρανίων σωμάτων, και μάλιστα με εξισώσεις γενικής σχετικότητας. Ο φυσικός καταλήγει σε μια απλή λύση κάνοντας τις λογικές υποθέσεις οτι το βλήμα διανύει κατά ύψος και κατά μήκος το πολύ μερικές εκατοντάδες μέτρα.

Αναλυτική σκέψη

Ένας κανόνας που ισχύει σχεδόν πάντα στη φυσική — τουλάχιστον στην κλασική — αλλά και στην επιστήμη γενικότερα, είναι οτι αν ένα πρόβλημα μπορεί να αναλυθεί σε δύο ή περισσότερα μέρη, και μελετήσουμε το κάθε μέρος χωριστά, τότε το αρχικό πρόβλημα δεν είναι παρά “το άθροισμα των μερών-του”.

Ένα παράδειγμα θα ξεκαθαρίσει αμέσως τον κανόνα αυτόν. Ας θεωρήσουμε και πάλι το πρόβλημα της τροχιάς ενός βλήματος μετά από βολή υπό γωνία (“πλάγια βολή”). Η λύση του προβλήματος αυτού είναι όπως είδαμε — μετά από κάποιες απλοποιητικές υποθέσεις — μια παραβολή, που είναι καμπύλη δύο διαστάσεων, x και y. Για να φτάσουμε στη λύση του προβλήματος, χρήσιμο είναι να αναλύσουμε το πρόβλημα στις δύο διαστάσεις-του, δηλ. να θεωρήσουμε το τί συμβαίνει ξεχωριστά στον οριζόντιο άξονα x και στον κατακόρυφο άξονα y (βλ. σχήμα που ακολουθεί).

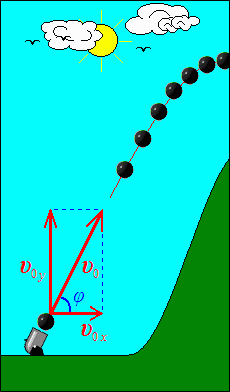
Στο παραπάνω διάγραμμα φαίνεται η γωνία φ υπό την οποία γίνεται η βολή, όπως και η αρχική ταχύτητα υ₀ (το πλάγιο κόκκινο βέλος). Αυτή η αρχική ταχύτητα υ₀ αναλύεται σε δύο συνιστώσες: στη συνιστώσα υ₀_x κατά τον οριζόντιο άξονα x, και στη συνιστώσα υ₀_y κατά τον κατακόρυφο άξονα y. Μάλιστα μπορούμε να υπολογίσουμε την κάθε συνιστώσα βάσει του υ₀ και του φ. Έχουμε λοιπόν οτι: υ₀_x = υ₀ συν(φ), και υ₀_y = υ₀ ημ(φ). Επομένως τώρα μπορούμε να υποθέσουμε οτι η τροχιά του βλήματος είναι η σύνθεση δύο ανεξάρτητων κινήσεων: μιας ευθύγραμμης ομαλής κίνησης πάνω στον οριζόντιο άξονα x με ταχύτητα υ₀_x, άρα η απόσταση s_x του βλήματος σαν συνάρτηση του χρόνου t δίνεται από τη σχέση: s_x(t) = υ₀_xt · και μιας κίνησης πάνω στον κατακόρυφο άξονα y με αρχική ταχύτητα υ₀_y, όπου επειδή επιδρά η επιτάχυνση της βαρύτητας g, η απόσταση s_y σαν συνάρτηση του χρόνου t δίνεται από τη σχέση: s_y(t) = υ₀_yt – ½ g t². Στο επόμενο διάγραμμα φαίνεται το οτι η οριζόντια συνιστώσα είναι ευθύγραμμη ομαλή, ενώ η κατακόρυφη συνιστώσα είναι σαν κατακόρυφη βολή κατά την οποία το βλήμα αρχικά ανεβαίνει, φτάνει στο μέγιστο ύψος, και μετά κατεβαίνει.

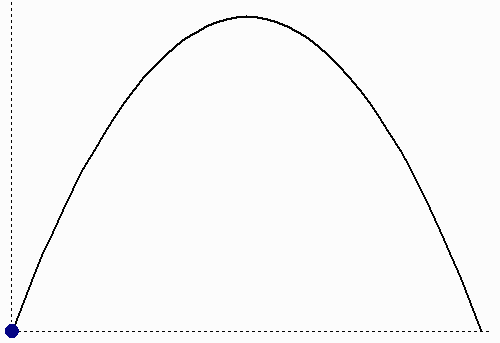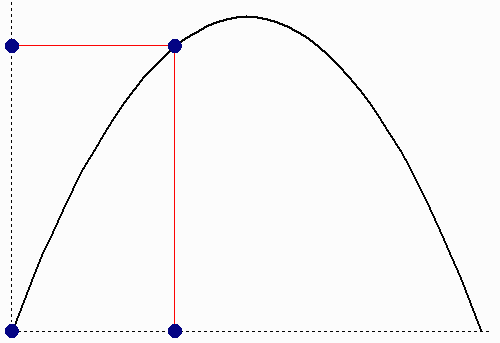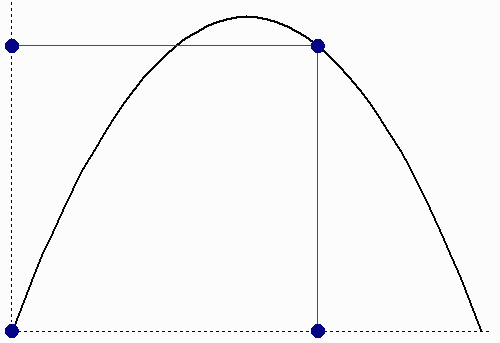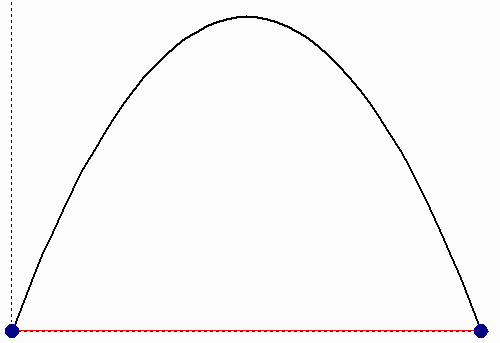
Η προβολή του βλήματος πάνω στον οριζόντιο άξονα x δίνει ευθύγραμμη ομαλή κίνηση,
ενώ η προβολή πάνω στον κατακόρυφο άξονα y δίνει ομαλά επιβραδυνόμενη–επιταχυνόμενη κίνηση

Από την προηγούμενη ανάλυση στις δύο συνιστώσες, έχουμε ήδη δημιουργήσει την παραμετρική εξίσωση της τροχιάς του βλήματος:

Παραμετρική εξίσωση τροχιάς:

x(t) = υ₀_xt
y(t) = υ₀_yt – ½ gt²

Αυτή ηπαραμετρική εξίσωση περιγράφει πράγματι μια παραβολή. Αν θέλουμε να δούμε την παραβολή αυτή σαν εξίσωση της μορφής y = f(x), δεν έχουμε παρά να λύσουμε την πρώτη σχέση ως προς t, οπότε παίρνουμε t = x / υ₀_x, και να αντικαταστήσουμε το t στη δεύτερη σχέση, οπότε παίρνουμε: y = (υ₀_y / υ₀_x) x – g (1 / 2υ₀_x) x². Αυτή η εξίσωση αναγνωρίζεται εύκολα σαν δευτεροβάθμια πολυωνυμική συνάρτηση (παραβολή), που έχει στραμμένο το κυρτό μέρος προς τα πάνω (λόγω του –x²).

Το παραπάνω είναι ένα τυπικό παράδειγμα “αναλυτικής σκέψης”. Δηλαδή, προκειμένου να λυθεί ένα σύνθετο πρόβλημα, πρώτα το αναλύουμε στα μέρη από τα οποία αποτελείται (εφόσον αυτό είναι δυνατό), λύνουμε το καθένα μέρος χωριστά, και στη συνέχεια ανασυνθέτουμε τα μέρη αποκτώντας το όλο, δηλαδή τη συνολική λύση.

Αφαίρεση – πυρήνας προβλήματος

Αν σκεφτούμε το πώς λύθηκε το πρόβλημα της τροχιάς της πλάγιας βολής, θα διαπιστώσουμε οτι ακολουθήθηκε μια διαδικασία αφαίρεσης. Δηλαδή, ενώ ξεκινήσαμε με ένα πρόβλημα που φαινομενικά έχει πάμπολλες παραμέτρους (βάρος και σχήμα βλήματος, αέρας που μπορεί να φυσάει, σύνθετη μορφολογία εδάφους, σύνθετη σχέση βαρύτητας, κανόνι που μπορεί να μην αναφλεγεί, κλπ.), αφαιρέσαμε όλες εκείνες τις παραμέτρους που δεν προσθέτουν τίποτε απολύτως στη λύση (π.χ. κατάσταση κανονιού, μορφολογία εδάφους, κλπ.), ή που απλώς προσθέτουν πολυπλοκότητα (π.χ. αντίσταση αέρα), και κρατήσαμε μόνο τον πυρήνα του προβλήματος. Αφού βρούμε τη λύση για τον πυρήνα του προβλήματος, μπορούμε στη συνέχεια να προσθέσουμε μία-μία άλλες παραμέτρους (π.χ. αντίσταση αέρα, βαρύτητα εξαρτώμενη απ’ το ύψος, κλπ) ώστε να αντιμετωπίσουμε μια πιο σύνθετη πραγματικότητα.

Η εμπειρική μέθοδος και οι συνέπειές της στη διατύπωση φυσικών νόμων

Μία παρανόηση που παρατηρείται συχνά ακόμη και μεταξύ φοιτητών της φυσικής είναι οτι οι νόμοι της φύσης ισχύουν με απόλυτο τρόπο, προβλέποντας οτι το μελλοντικό γεγονός “οφείλει” να ακολουθήσει τους νόμους αυτούς. Στην πραγματικότητα, όταν διατυπώνουμε ένα φυσικό “νόμο” τον διατυπώνουμε απλώς εμπειρικά, δηλαδή πάντα με κάποια — στοιχειώδη έστω — επιφύλαξη, χωρίς να υποθέτουμε οτι υποχρεωτικά πρέπει να ισχύει στο 100% των μελλοντικών παρατηρήσεων (επειδή τάχα είναι “νόμος”). Ας πάρουμε το νόμο της βαρύτητας σαν ένα ακραίο παράδειγμα. Αν αφήσουμε ελεύθερο ένα μολύβι που κρατάμε με το χέρι, ο νόμος της βαρύτητας λέει — μεταξύ άλλων — οτι το μολύβι θα κινηθεί προς τα κάτω (προς το κέντρο της Γης). Ο νόμος αυτός έχει επαληθευτεί τόσες πολλές φορές που είναι δύσκολο ακόμα και να εκτιμήσουμε τον αριθμό των επαληθεύσεων, καθώς ο κάθε άνθρωπος επαληθεύει αρκετές φορές την ημέρα το οτι τα αντικείμενα που αφήνονται ελεύθερα (και είναι βαρύτερα του αέρα — ας εξαιρέσουμε τα μπαλόνια ηλίου, κλπ.) κινούνται προς τα κάτω· κανείς ποτέ δεν παρατήρησε ένα αντικείμενο που κινήθηκε προς άλλη κατεύθυνση. Αυτός όμως είναι και ο μόνος λόγος που έχουμε τόσο μεγάλη εμπιστοσύνη στο νόμο της βαρύτητας: οτι δεν υπήρξε ποτέ ούτε μία διάψευση. Δεν σημαίνει όμως αυτό οτι δεν μπορεί να υπάρξει ποτέ καμία διάψευση. Δεν μπορούμε να συμπεράνουμε ποτέ το απόλυτο της ισχύος του νόμου αυτού (ή και κάθε άλλου νόμου), επειδή δεν έχουμε δει καμία διάψευση μέχρι τώρα.

Ας δούμε ένα παράδειγμα του πώς θα μπορούσε να διαψευστεί ο νόμος της βαρύτητας — παράδειγμα που κανείς φυσικός δεν πιστεύει οτι θα μπορούσε να ισχύει, αλλά δίνεται εδώ απλώς σαν “πείραμα σκέψης”. Θα μπορούσε να συμβαίνει οτι αν μεταφερθούμε στα 2/3 της ακτίνας ενός ουράνιου σώματος (αστέρα, πλανήτη), πάνω από το βόρειο ή το νότιο πόλο του σώματος αυτού, θα βρούμε εκεί ένα σημείο όπου η βαρύτητα “αντιστρέφεται”· αν δηλαδή αφήσουμε εκεί ένα μολύβι ελεύθερο, αυτό θα κινηθεί απωθούμενο απ’ το σημείο (προς τυχαία διεύθυνση αν το αφήσουμε ακριβώς στο σημείο εκείνο). Η περιοχή αυτή της “αντίστροφης βαρύτητας” θα μπορούσε να είναι σφαιρική με κέντρο το σημείο, και με ακτίνα ίση με το ένα εκατομμυριοστό της ακτίνας του ουράνιου σώματος (πράγμα που για τη Γη αντιστοιχεί σε ~6,37 μέτρα)· στη δε επιφάνεια της σφαίρας αυτής (στο όριο μεταξύ αντίστροφης και κανονικής βαρύτητας), η βαρύτητα θα μπορούσε να μηδενίζεται. Κανείς ποτέ δεν παρατήρησε τα δύο αυτά αντιδιαμετρικά σημεία, γιατί οι σφαιρικές περιοχές-τους είναι πολύ μικρές και πολύ μακριά έξω από την ατμόσφαιρα της Γης, οπότε κανένας δορυφόρος δεν έτυχε να “πέσει” στα σημεία εκείνα. Φυσικά (για να ολοκληρώσουμε το παράδειγμα κάνοντάς το πιο πιστευτό), τέτοιες περιοχές υπάρχουν και σε ανάλογη απόσταση από περιστρεφόμενα σώματα με οποιαδήποτε μάζα (π.χ. έναν ανεμιστήρα), αλλά είναι τόσο μικρές που είναι πρακτικά αδύνατο να ανιχνευτούν, και εν πάση περιπτώσει κανείς φυσικός δεν σκέφτηκε ποτέ να ανιχνεύσει μια τέτοια “ανωμαλία” στο νόμο της βαρύτητας.

Υποτιθέμενα σημεία αντίστροφης βαρύτητας, σε ορισμένη απόσταση από τους δύο πόλους της Γης

Το παραπάνω παράδειγμα μας δείχνει οτι η έννοια “φυσικός νόμος” δεν πρέπει να ερμηνεύεται με απόλυτο τρόπο. Ο φυσικός δεν είναι ποτέ 100% βέβαιος οτι “κατέχει την αλήθεια” για το πώς λειτουργεί η φύση. Όταν διατυπώνει ένα φυσικό νόμο, το κάνει πάντα με την επιφύλαξη οτι μπορεί ο νόμος αυτός να διαψευστεί στο μέλλον, οπότε θα χρειαστεί βελτίωση ή συμπλήρωση. Η διατύπωση του νόμου γίνεται επειδή μέχρι στιγμής ο νόμος δεν έχει διαψευστεί, απ’ όσο μπορεί να γνωρίζει ο φυσικός. Βέβαια, όσο πιο πολλές φορές έχει υπάρξει επαλήθευση, τόσο πιο μεγάλη είναι η βεβαιότητά μας οτι το επόμενο φυσικό γεγονός θα ακολουθήσει το γνωστό νόμο. Μέχρι εκεί όμως φτάνει η γνώση-μας για τη φύση: ως ένα ποσοστό βεβαιότητας οτι τα μελλοντικά γεγονότα θα συμβούν με τον προβλεπόμενο τρόπο· ποτέ με την απόλυτη βεβαιότητα οτι όντως θα συμβούν έτσι. Άρα η φυσική (και κατ’ επέκταση οποιαδήποτε επιστήμη) είναι μια εμπειρική επιστήμη, βασιζόμενη κατ’ αποκλειστικότητα στην παρατήρηση, και όχι στην πίστη οτι έχουν τεθεί αναλλοίωτοι “νόμοι” στο σύμπαν στους οποίους τάχα “οφείλουν” να υπακούουν όλες οι μελλοντικές-μας παρατηρήσεις.

Η αρχή διατήρησης της ενέργειας

Μια άλλη σημαντική αρχή που μας βοηθά να λύσουμε προβλήματα φυσικής είναι η αρχή της διατήρησης της ενέργειας.

Η αρχή αυτή λέει οτι η ενέργεια μεταξύ δύο καταστάσεων ενός σώματος παραμένει αναλλοίωτη. (Θυμίζουμε οτι είμαστε στον τομέα της κλασικής φυσικής, όπου παραβλέπουμε το οτι στη μοντέρνα φυσική η ενέργεια μπορεί να μετατραπεί σε μάζα, και η μάζα σε ενέργεια.)

Ας πάρουμε το απλούστατο παράδειγμα ενός σώματος μάζας m που πέφτει κατακόρυφα από ύψος h στο έδαφος.

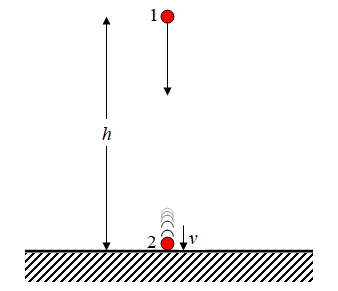
Όπως δείχνει το παραπάνω διάγραμμα, το σώμα (κόκκινο), όταν φτάνει στο έδαφος έχει αναπτύξει ταχύτητα v. Αυτή την ταχύτητα v θα την υπολογίσουμε χρησιμοποιώντας την αρχή διατήρησης της ενέργειας. Η αρχή διατήρησης της ενέργειας λέει οτι η ενέργεια του σώματος στη θέση 1 (άνω) και στη θέση 2 (κάτω) είναι η ίδια, διατηρείται, παρά την κίνηση που πραγματοποιεί το σώμα.

Στη θέση 1 (άνω), το σώμα έχει ενέργεια Ε₁ που είναι άθροισμα κινητικής Κ και δυναμικής U, δηλαδή Ε₁ = Κ + U. Γνωρίζουμε οτι η κινητική ενέργεια Κ δίνεται από τον τύπο: Κ = ½ mv². Επειδή όμως η ταχύτητα v στη θέση 1 είναι 0, έπεται οτι Κ = 0. Η δυναμική ενέργεια U του σώματος μάζας m είναι U = mgh, όπου g η επιτάχυνση της βαρύτητας και h το δοσμένο ύψος. Συνολικά λοιπόν, στη θέση 1 η ολική ενέργεια είναι Ε₁ = Κ + U = 0 + mgh = mgh.

Στη θέση 2 (κάτω), την ώρα που χτυπάει στο έδαφος, το σώμα έχει αναπτύξει ταχύτητα v, ενώ το ύψος-του είναι 0. Συνεπώς η ολική ενέργεια Ε₂ είναι: Ε₂ = Κ + U = ½ mv² + 0 = ½ mv².

Εφόσον από την αρχή διατήρησης της ενέργειας έχουμε οτι Ε₁ = Ε₂, έπεται οτι mgh = ½ mv². Από τη σχέση αυτή, απλοποιώντας το m από τα δύο μέλη (άρα συμπεραίνοντας οτι η τελική ταχύτητα είναι ανεξάρτητη της μαζας του σώματος — ιδέα που αποτέλεσε μια στιγμή «Εύρηκα!» για τον Γαλιλαίο, τον 16^ο-17^ο αιώνα), και λύνοντας ως προς v, παίρνουμε την τελική σχέση:

που είναι και η ζητούμενη σχέση για την τελική ταχύτητα v.

Ας σημειώσουμε εδώ οτι για τη λύση του προβλήματος αυτού κάναμε κάποιες αφαιρετικές υποθέσεις (βλ. παράγραφο “Αφαίρεση – πυρήνας προβλήματος”, παραπάνω). Συγκεκριμένα, υποθέσαμε σιωπηρά οτι δεν υπάρχει αντίσταση του αέρα (που ο Γαλιλαίος γνώριζε οτι υπάρχει, γιαυτό δεν πραγματοποίησε ποτέ το υποτιθέμενο πείραμα της ρίψης δύο σφαιρών, ξύλινης και μεταλλικής, από τον Πύργο της Πίζας)· οτι το ύψος h είναι πολύ μικρό ως προς την ακτίνα της Γης (επομένως η επιτάχυνση της βαρύτητας g παραμένει αναλλοίωτη καθ’ όλη την πτώση)· οτι δεν υπάρχει απώλεια ενέργειας λόγω θερμότητας ή εισροή ενέργειας λόγω ακτινοβολίας · και πιθανώς και άλλα διάφορα. Πάντοτε επιζητούμε πρώτα την απλή, αφαιρετική διατύπωση του προβλήματος στη φυσική, και αν υπάρχει λόγος, τότε προσθέτουμε την απαιτούμενη πολυπλοκότητα.

Θεμελιώδεις Αρχές και Εξέλιξη Φυσικής

Τί είναι η κλασική φυσική και σε τί διαφέρει από τη μοντέρνα φυσική