Δ.Ε.Π. : Μάθημα Υ2 : Προγραμματισμός υπολογιστών

Το μάθημα αυτό προϋποθέτει γνώση ορισμένων εννοιών περί υπολογιστών, που περιλαμβάνονται στο μάθημα Υ1. Συγκεκριμένα, υποτίθεται οτι ο διδασκόμενος γνωρίζει ως ένα βαθμό τις παρακάτω έννοιες:

Φυσικά, όσο πιο καλό είναι το υπόβαθρο από το μάθημα Υ1, με τόσο μεγαλύτερη ευκολία ο διδασκόμενος θα κατανοήσει το περιεχόμενο του παρόντος μαθήματος, Υ2. Πάντως οι παραπάνω έννοιες δεν θα εξηγηθούν στο παρόν· η γνώση-τους θα θεωρηθεί δεδομένη.

Στόχος, μέθοδος, και εργαλείο

Στο Υ2 θα μάθουμε να προγραμματίζουμε υπολογιστές, ξεκινώντας από το “απόλυτο μηδέν”, δηλαδή θεωρώντας μηδενική γνώση εννοιών προγραμματισμού εκ μέρους του διδασκομένου. Για να φτάσουμε να γράψουμε το πρώτο, απλούστατο πρόγραμμά μας όμως, χρειάζεται να εξοικειωθούμε πρώτα — έστω στοιχειωδώς — με το εργαλείο που θα μας επιτρέψει να προγραμματίσουμε. Κατ’ αναλογία, αν στόχος-μας ήταν να μάθουμε να συνθέτουμε μουσική, θα έπρεπε βέβαια να αποκτήσουμε ένα μουσικό όργανο, π.χ. μία κιθάρα· αλλά δεν θα αρκούσε απλώς να την αποκτήσουμε· θα έπρεπε να μάθουμε και πώς να χειριζόμαστε την κιθάρα. Κάτι ανάλογο ισχύει και στον προγραμματισμό: για να μάθουμε να “συνθέτουμε προγράμματα” υπάρχουν βέβαια πολλά “όργανα”, αλλά εμείς θα επικεντρωθούμε σε ένα, με το οποίο θα μάθουμε να προγραμματίζουμε σε μια τυπική (“μέση”) γλώσσα προγραμματισμού, τη γλώσσα Java. Το εργαλείο αυτό λέγεται JBuilder 7, διατίθεται δωρεάν από το Δ.Ε.Π. στον διδασκόμενο (είναι ελεύθερο πνευματικών δικαιωμάτων), και υποτίθεται οτι πριν να προχωρήσουμε στο παρόν μάθημα, ο διδασκόμενος το έχει ήδη προμηθευτεί από το Δ.Ε.Π. σε συνεννόηση με τον διδάσκοντα του παρόντος μαθήματος.

Υποχρεωτικά προκαταρκτικά βήματα

Για να ξεκινήσουμε λοιπόν να κάνουμε χρήση της “κιθάρας-μας” (δηλαδή του JBuilder 7), πρέπει πρώτα να την “κουρδίσουμε”. Το πώς γίνεται αυτό εξηγείται στη σελίδα αυτή, τις οδηγίες της οποίας ο αναγνώστης θα πρέπει τώρα να ακολουθήσει. (Κάνοντας κλικ στο σύνδεσμο, οι οδηγίες ανοίγουν σε νέο παράθυρο.)

Στο υπόλοιπο του μαθήματος θεωρούμε οτι, ακολουθώντας τις οδηγίες της σελίδας του παραπάνω συνδέσμου, έχουμε φτιάξει το πρώτο-μας project, το Minimal· και επιπλέον, χρησιμοποιώντας σαν βάση το Minimal, έχουμε φτιάξει επίσης το δεύτερό μας project, το Geometry, που προς το παρόν περιλαμβάνει ότι και το Minimal, συν μία τάξη, την Circle. Κατά τα άλλα, το project Geometry περιμένει να του προσθέσουμε τα προγράμματά μας.

1. Οι τρεις θεμελιώδεις δομές προγραμματισμού

Υπάρχουν τρεις θεμελιώδεις δομές μέσω των οποίων γράφουμε όλα τα προγράμματα στις “δηλωτικές” (αγγλ.: declarative) γλώσσες προγραμματισμού όπως η Java, με την οποία θα ασχοληθούμε στο μάθημα αυτό. Οι δομές αυτές είναι:

Ας δούμε τώρα καθεμία προγραμματιστική δομή χωριστά.

1.1 Η ακολουθία εντολών

Έστω οτι αντί για πρόγραμμα σε υπολογιστή, αυτό που θέλουμε να φτιάξουμε (να “υλοποιήσουμε”) είναι μια συνταγή για τσουρέκια. Κάθε συνταγή αποτελείται από ορισμένα “βήματα” που πρέπει να εκτελεστούν με μια ορισμένη σειρά. Π.χ. η συγκεκριμένη συνταγή μπορεί να περιλαμβάνει αρχικά τα εξής βήματα:

Τα βήματα αυτά είναι μια ακολουθία εντολών. Προφανώς οι εντολές πρέπει να εκτελεστούν με τη σωστή σειρά, όπως καθορίζει η συνταγή. Π.χ. στο βήμα 2 το γάλα πρέπει να είναι χλιαρό, άρα δεν μπορούμε να ξεκινήσουμε κατευθείαν με το βήμα 2 γιατί πρέπει να έχει προηγηθεί το βήμα 1. Στην παραπάνω συνταγή, το κάθε βήμα εξαρτάται από το αν τελείωσε το προηγούμενό του. Το ίδιο ισχύει και στα προγράμματα. Τα βήματα εκτελούνται πάντα ένα-ένα, “ακολουθιακά” (τουλάχιστον στο είδος των υπολογιστών που βρίσκονται γύρω-μας, και λόγω του τρόπου που τους προγραμματίζουμε). Βέβαια, δεν είναι υποχρεωτικό να εξαρτάται το κάθε βήμα από τα προηγούμενά του, δηλαδή να υπάρχει λογική εξάρτηση. Π.χ. η συνταγή-μας θα μπορούσε να λέει οτι πρώτα ρίχνουμε το αλεύρι στο γάλα, το ανακατεύουμε λίγο, και μετά προσθέτουμε τη μαγιά. Αυτό ίσως να επιτρέπεται γιατί ο σκοπός είναι να μπουν τόσο η μαγιά όσο και το αλεύρι μέσα στο χλιαρό γάλα, χωρίς να έχει σημασία ποιο θα μπει πρώτα και ποιο ύστερα. Πάντως αν η συνταγή αυτή ήταν ένα πρόγραμμα, εφόσον λέει οτι πρώτα θα μπει η μαγιά και μετά το αλεύρι, έτσι θα γίνει, μ’ αυτή τη σειρά. Δεν πρόκειται να αναλάβει πρωτοβουλίες το πρόγραμμά μας και να εκτελέσει τα βήματα της συνταγής με άλλη σειρά από αυτήν που εμείς ορίζουμε.

Ας γράψουμε τώρα μερικές πραγματικές εντολές προγράμματος σαν ακολουθία εντολών, και ας τις εκτελέσουμε για να δούμε το αποτέλεσμά τους.

Θα ζωγραφίσουμε τρεις κύκλους στην οθόνη, που το εσωτερικό-τους θα είναι του πρώτου κόκκινο, του δεύτερου κίτρινο, και του τρίτου πράσινο. Τις γραμμές κώδικα που δημιουργούν και ζωγραφίζουν αυτούς τους κύκλους θα τους βάλουμε στη μέθοδο paint της τάξης AppPanel του project Geometry. Κάνουμε τα παρακάτω:

Σημειώστε οτι “ακολουθία εντολών” είναι ουσιαστικά και τα παραπάνω βήματα, 1 έως 6, μόνο που δεν είναι προγραμματιστικές εντολές, αλλά μοιάζουν περισσότερο με τις οδηγίες της συνταγής μαγειρικής που αναφέρθηκε πρωτύτερα. Πραγματική ακολουθία εντολών είναι οι έξι εντολές που δίνονται στο βήμα 5. Οι τρεις πρώτες δημιουργούν τους τρεις κύκλους, και οι τρεις επόμενες τους εμφανίζουν στην οθόνη με τα χρώματα που αποφασίσαμε.

Επίσης σημειώστε οτι δεν είναι απαραίτητο πρώτα να δημιουργήσουμε καί τους τρεις κύκλους και έπειτα να τους εμφανίσουμε όλους μαζεμένους. Μπορούμε να τους δημιουργήσουμε και να τους εμφανίσουμε έναν-έναν, όπως στην επόμενη ακολουθία εντολών:

Πάντως για καθέναν από τους circle1, circle2, και circle3 ισχύει οτι πρέπει πρώτα να δημιουργηθεί (με τον “τελεστή” new της Java) και έπειτα να εμφανιστεί στην οθόνη (με τη μέθοδο Paint της τάξης Circle).

Για την κατανόηση των παραπάνω ενολών, θα σημειώσουμε τα εξής:

Μια εντολή “δημιουργίας αντικειμένου”, όπως η:

λέει το εξής: δημιούργησε ένα νέο (new) αντικείμενο, το circle1, που να είναι της τάξης (δηλ. του τύπου) Circle, και βάλε το κέντρο του κύκλου στις συντεταγμένες τις οθόνης x = 200 και y = 200, όπως και την ακτίνα του κύκλου να είναι ίση με 50 pixels. Το οτι αυτές οι τρεις τιμές ορίζουν το κέντρο και την ακτίνα του κύκλου το καθορίζει αυτό που ονομάζεται “κατασκευαστής” της τάξης Circle, και που τον έχουμε ορίσει εμείς όταν προσθέσαμε τον κώδικα της τάξης Circle στο project Geometry. Περισσότερα περί κατασκευαστών αργότερα, όταν θα μάθουμε για τα χαρακτηριστικά των τάξεων.

Η εντολή που εμφανίζει (ζωγραφίζει) τον κύκλο στην οθόνη,

λέει το εξής: κάλεσε τη μέθοδο Paint του αντικειμένου circle1 (που δημιουργήθηκε πρωτύτερα), και πέρασέ της τρεις παραμέτρους: το g, που είναι το αντικείμενο μέσω του οποίου ζωγραφίζουμε γραφικά στην οθόνη, το null, που είναι το χρώμα της περιφέρειας του κύκλου (όπου “null” σημαίνει “κανένα χρώμα”), και το Color.red, το χρώμα με το οποίο γεμίζουμε το εσωτερικό του κύκλου.

Σημειώστε οτι η κάθε εντολή στη Java (είτε δημιουργίας αντικειμένου, είτε ζωγραφίσματος, είτε οτιδήποτε) τελειώνει πάντα με ένα semicolon (“;”, το ελληνικό ερωτηματικό).

Επίσης ίσως προσέξατε οτι μερικές λέξεις κώδικα, όπως τα new και null, είναι σε έντονη γραφή. Αυτό είναι μια απλή σύμβαση που ακολουθεί το JBuilder IDE, εμφανίζοντάς μας έτσι τις λέξεις που “ξέρει” η Java: τις λέξεις-κλειδιά, ή keywords της γλώσσας, όπως λέγονται. Η έντονη γραφή δεν είναι σύμβαση της ίδιας της Java. Θα μπορούσαμε δηλαδή να γράψουμε τον πηγαίο κώδικά μας σε έναν απλό επεξεργαστή κειμένου, π.χ. στο Nodepad των Windows, όπου βέβαια δεν έχουμε τη δυνατότητα έντονης γραφής

· και πάλι όμως το πρόγραμμά μας θα ήταν ολόσωστο. Η έντονη γραφή, με άλλα λόγια, είναι ένα οπτικό εφφέ του JBuilder IDE. Το ίδιο ισχύει και με τα άλλα εφφέ που βλέπουμε στον πηγαίο κώδικά μας, όπως π.χ. τα χρώματα των ακεραίων αριθμών και των σχολίων.

Άσκηση 1.1: Γράψτε δύο επιπλέον εντολές μετά από τις παραπάνω έξι, που η πρώτη να δημιουργεί έναν 4^ο κύκλο (σε όποια θέση της οθόνης και με όποια ακτίνα θέλετε) και η δεύτερη να τον εμφανίζει με όποιο χρώμα θέλετε. (Υπάρχουν τα Color.blue, Color.cyan, Color.black, Color.magenta, Color.pink, Color.orange, και άλλα· υπάρχουν διαθέσιμα στην πραγματικότητα 16 εκατομμύρια χρώματα, αλλά φυσικά δεν τα καθορίζουμε μέσω ονομάτων αλλά μέσω άλλου τρόπου, που θα μάθουμε αργότερα.) Εκτελέστε το πρόγραμμά σας, και διαπιστώστε οτι παρουσιάζει τον τέταρτο κύκλο έτσι ακριβώς όπως τον φανταστήκατε.

1.2 Ο λογικός έλεγχος (η εντολή “if

”)

Μια συνταγή (ή “αλγόριθμος”) δεν είναι απαραίτητο να μοιάζει πάντα με μια ακολουθία εντολών. Π.χ. η αρχική συνταγή μαγειρικής μπορεί στο πρώτο βήμα να λέει το εξής: «Αν υπάρχει φούρνος μικροκυμάτων, τότε χλιαρεύουμε το γάλα εκεί για 1 λεπτό· αλλιώς το χλιαρεύουμε στο μάτι της κουζίνας για 3 λεπτά.» Υπάρχει δηλαδή ο εξής λογικός έλεγχος: «Υπάρχει φούρνος μικροκυμάτων;» Αν ναι, τότε κάνουμε ένα πράγμα· αλλιώς κάνουμε άλλο πράγμα. (Οι έντονες λέξεις και η άνω τελεία δεν τέθηκαν εδώ χωρίς λόγο.)

Πίσω στο πρόγραμμά μας τώρα, όπου θα κάνουμε κάτι διαφορετικό. Δεν θα εμφανίζουμε κύκλους με το που ξεκινάει το πρόγραμμα, αλλά ο κύκλος θα εμφανίζεται στο σημείο όπου κάνουμε κλικ με το ποντίκι πάνω στη λευκή επιφάνεια του παραθύρου του προγράμματος. (Δηλ. το κέντρο του κύκλου θα είναι στο σημείο του κλικ.) Το δε χρώμα του κύκλου θα είναι κόκκινο αν το κέντρο-του είναι στο αριστερό μισό του παραθύρου, και πράσινο αν είναι στο δεξί μισό.

Καταρχήν, ορισμένα απαραίτητα τεχνικά βήματα:

Πρώτο, πρέπει να σβήσουμε τις γραμμές κώδικα που έχουμε βάλει στη μέθοδο paint της τάξης AppPanel. Επομένως η paint πρέπει να έχει τώρα την αρχική-της μορφή, όπως όταν την είχαμε πρωτοδημιουργήσει στα projects Minimal και Geometry:

public void paint (Graphics g) {
   int width = getBounds().width;
   int height = getBounds().height;
   if ( ! screenPainted) {
      screenPainted = true;
      // Code specifying what must happen only once (i.e., initializations)
      // when the window of the program has just opened, goes here.
   }
   // Code painting things every time the window of the program needs to
   // be painted goes here.
}

Δεύτερο, πρέπει να κάνουμε το πρόγραμμά μας να ανταποκρίνεται στο κλικ του ποντικιού. Αυτό γίνεται σε μια άλλη μέθοδο της AppPanel, που λέγεται mouseReleased και βρίσκεται ακριβώς πάνω από την paint. H mouseReleased εμφανίζεται ως εξής:

public void mouseReleased(MouseEvent e) {
   e.consume();
   Point point = new Point (e.getX(), e.getY());
   //! Code specifying what happens when clicking anywhere goes here.
}

Στο σημείο που είναι το σχόλιο μπορούμε να γράψουμε τον παρακάτω κώδικα (σβήνοντας εντελώς το σχόλιο που αρχίζει με “//!” και αντικαθιστώντας-το με τις ακόλουθες γραμμές):

   // Draw a red circle if click is on the left half, green if on the right.
   Graphics g = getGraphics();        // prepare to do graphics.
   int width = getBounds().width;     // get the screen width...
   int height = getBounds().height;   // ...and height (for later use).
   Circle circle = new Circle (point.x, point.y, 50);    // create circle.
   if (point.x < width / 2) {                            // if on the left,
      circle.Paint (g, null, Color.red);                 // then red;
   }
   else {
      circle.Paint (g, null, Color.green);               // else green.
   }
   g.dispose();                       // get rid of the Graphics object.

Με τις τέσσερις πρώτες γραμμές δημιουργούμε ένα αντικείμενο γραφικών, μαθαίνουμε το πλάτος και το ύψος του παραθύρου (το ύψος δεν θα μας χρειαστεί προς το παρόν), και δημιουργούμε έναν κύκλο με κέντρο στο σημείο όπου έγινε το κλικ, και με δοσμένη διάμετρο (50 pixels).

Στη συνέχεια πρέπει να ελέγξουμε αν το κλικ έγινε στο αριστερό ή στο δεξί μισό του παραθύρου. Αυτός ο λογικός έλεγχος γίνεται με την εντολή if που ακολουθεί. Όπως βλέπουμε, ο λογικός έλεγχος της εντολής κλείνεται μέσα σε παρενθέσεις. Στην περίπτωσή μας, ο έλεγχος λέει: “αν η x-συντεταγμένη του σημείου του κλικ είναι μικρότερη από το πλάτος του παραθύρου διά 2”· με άλλα λόγια, “αν το κλικ έγινε στο αριστερό μισό του παραθύρου”. Μετά από τον έλεγχο γράφουμε μέσα σε ένα ζευγάρι αγκίστρων ({}) το τί θέλουμε να συμβεί τότε. Όπως αποφασίσαμε, αυτό που θέλουμε να συμβεί είναι να ζωγραφιστεί ένας κόκκινος κύκλος. Αυτό ακριβώς κάνει η εντολή circle.Paint (g, null, Color.red). Ακολουθεί το “αλλιώς” (“else part”) της εντολής. Κι αυτό κλείνεται σε ένα ζεγάρι άγκιστρα, και στην περίπτωσή μας ζωγραφίζεται ένας κύκλος πράσινου χρώματος.

Μετά από την εντολή if ακολουθεί μια προαιρετική εντολή που διαγράφει (“πετάει στα άχρηστα”) το αντικείμενο των γραφικών. Η εντολή αυτή είναι η g.dispose().

Βλέπουμε λοιπόν οτι η εντολή if αποτελείται από τρία μέρη: τον έλεγχο, την περιοχή “τότε”, και την περιοχή “αλλιώς”.

Παράδειγμα αποτελέσματος εκτέλεσης του προγράμματος με λογικό έλεγχο.

Άσκηση 1.2: Βρείτε πώς πρέπει να αλλάξετε το λογικό έλεγχο ώστε να ζωγραφίζονται κόκκινοι κύκλοι στο άνω μισό του παραθύρου, και πράσινοι στο κάτω μισό.

Ας σημειώσουμε οτι μέσα στο κάθε ζευγάρι αγκίστρων μπορούμε να γράψουμε μια ολόκληρη ακολουθία εντολών. Αυτό έχουμε κάνει παραπάνω, μόνο που η καθεμία από τις δυο ακολουθίες-μας έχει μόνο μία εντολή. Θα μπορούσε να έχει δύο ή περισσότερες εντολές. Παραδείγματος χάρη (αν και αυτό δεν είναι σωστή προγραμματιστική πρακτική) την εντολή που διαγράφει το αντικείμενο γραφικών θα μπορούσαμε να την επαναλάβουμε τόσο στην περιοχή του “τότε” όσο και στην περιοχή του “αλλιώς”, ως εξής:

   if (point.x < width / 2) {
      circle.Paint (g, null, Color.red);
      g.dispose();
   }
   else {
      circle.Paint (g, null, Color.green);
      g.dispose();
   }

Θα σημειώσουμε τώρα και το εξής: αν η ακολουθία εντολών αποτελείται από μια μόνο εντολή τότε τα άγκιστρα δεν είναι απαραίτητα. Έτσι, το αρχικό παράδειγμα θα μπορούσε να γραφεί ως εξής:

Γενικά οι προγραμματιστές προτιμούν να γράφουν κώδικα που να πιάνει όσο το δυνατό μικρότερο χώρο· η μη-χρησιμοποίηση των αγκίστρων όταν η ακολουθία εντολών αποτελείται κατά τεριμμένο τρόπο από μία εντολή είναι ένα είδος “λακωνίζειν”, γιαυτό και προτιμάται.

Ας υποθέσουμε τώρα οτι θέλουμε το χρώμα του κύκλου να εξαρτάται από το σε ποιο τέταρτο του παραθύρου γίνεται το κλικ. Πιο συγκεκριμένα:

Η λογική του προγράμματός μας τώρα επομένως λέει: αν το κλικ έγινε στο αριστερό μέρος (πρώτες δύο συνθήκες από την παραπάνω λίστα), τότε: αν έγινε πάνω, τότε κόκκινος κύκλος, αλλιώς μπλε· αλλιώς αν έγινε στο δεξί μισό (τελευταίες δύο συνθήκες), τότε: αν πάνω πράσινος, αλλιώς κίτρινος. Ας αποτυπώσουμε αυτή τη λογική σε κώδικα προγράμματος:

   if (point.x < width / 2) {                            // if on the left,
      if (point.y < height / 2)                          // and upper-half
         circle.Paint (g, null, Color.red);              // then red;
      else                                               // else lower-half,
         circle.Paint (g, null, Color.blue);             // hence blue.
   }
   else {                                                // else on the right
      if (point.y < height / 2)                          // and upper-half
         circle.Paint (g, null, Color.green);            // then green;
      else                                               // else lower-half,
         circle.Paint (g, null, Color.yellow);           // hence yellow.
   }

Θα κάνουμε όμως και την εξής παρατήρηση: αυτό που περιλαμβάνεται σαν “ακολουθία εντολών” στην περιοχή του “τότε” του πρώτου if είναι μία μόνο εντολή: η εντολή if (που βέβαια έχει τις δικές-της περιοχές “τότε-αλλιώς”). Επομένως, σύμφωνα με τα όσα μόλις μάθαμε, μπορούμε να βγάλουμε το πρώτο ζευγάρι των αγκίστρων. Το ίδιο μπορούμε να κάνουμε και για το δεύτερο ζευγάρι (στην περιοχή “αλλιώς” του πρώτου if). Μετά την αφαίρεση των αγκίστρων, ο κώδικάς μας γράφεται ως εξής:

   if (point.x < width / 2)                              // if on the left,
      if (point.y < height / 2)                          // and upper-half
         circle.Paint (g, null, Color.red);              // then red;
      else                                               // else lower-half,
         circle.Paint (g, null, Color.blue);             // hence blue.
   else                                                  // else on the right
      if (point.y < height / 2)                          // and upper-half
         circle.Paint (g, null, Color.green);            // then green;
      else                                               // else lower-half,
         circle.Paint (g, null, Color.yellow);           // hence yellow.

public void mouseReleased(MouseEvent e) {
   e.consume();
   Point point = new Point (e.getX(), e.getY());
   // Draw a red circle if click is on the upper-left quarter,
   // blue if on the lower-left,
   // green if on the upper-right, and
   // yellow if on the lower-right.
   Graphics g = getGraphics();        // prepare to do graphics.
   int width = getBounds().width;     // get the screen width...
   int height = getBounds().height;   // ...and height (for later use).
   Circle circle = new Circle (point.x, point.y, 50);    // create circle.
   if (point.x < width / 2)                              // if on the left,
      if (point.y < height / 2)                          // and upper-half
         circle.Paint (g, null, Color.red);              // then red;
      else                                               // else lower-half,
         circle.Paint (g, null, Color.blue);             // hence blue.
   else                                                  // else on the right
      if (point.y < height / 2)                          // and upper-half
         circle.Paint (g, null, Color.green);            // then green;
      else                                               // else lower-half,
         circle.Paint (g, null, Color.yellow);           // hence yellow.
   g.dispose();                       // get rid of the graphics object.
}

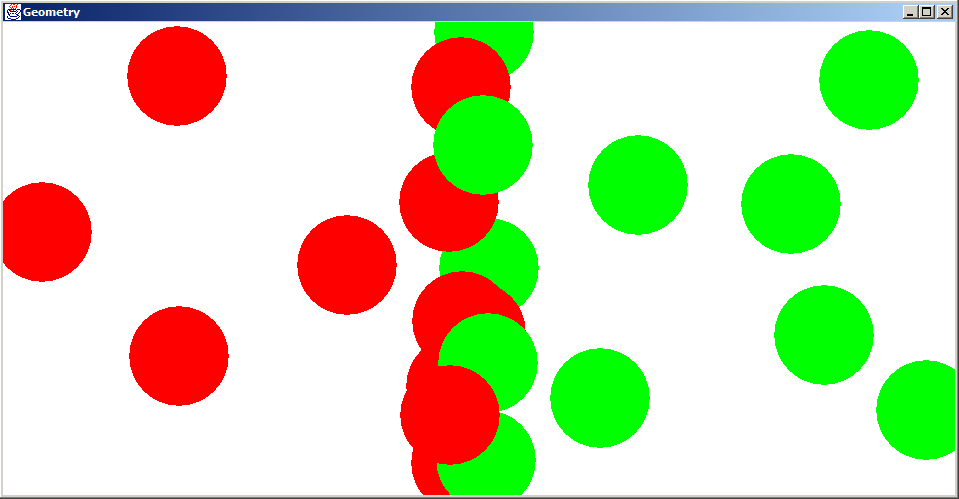
Ένα αποτέλεσμα εκτέλεσης του προγράμματος φαίνεται στην παρακάτω εικόνα:

Παράδειγμα αποτελέσματος εκτέλεσης του προγράμματος με διπλό λογικό έλεγχο.

Άσκηση 1.3: Κάντε τους κύκλους να είναι κόκκινοι αν η x-συντεταγμένη του σημείου του κλικ είναι αριθμός άρτιος (διαιρετός δια 2), και πράσινοι αν είναι αριθμός περιττός. Ελέγχουμε αν ένας αριθμός x είναι άρτιος με τον εξής τρόπο: if (x % 2 == 0). Τις έννοιες του τελεστή % (που δεν έχει καμία σχέση με το “επί τοις εκατό” αλλά διαβάζεται: “υπόλοιπο”), όπως και του διπλού ίσον (==), θα τις συναντήσουμε αργότερα, και αρκετά σύντομα. Βέβαια όταν εκτελέσετε το πρόγραμμα της άσκησης αυτής δεν θα έχετε τρόπο να γνωρίζετε αν οι κύκλοι είναι του “σωστού” χρώματος, εφόσον δεν είναι καθόλου προφανές το σε ποια συντεταγμένη έγινε το κλικ. Θα βλέπετε κύκλους με μάλλον “τυχαία” κόκκινο ή πράσινο χρώμα.

Άσκηση 1.4: Τροποποιήστε το πρόγραμμα τις προηγούμενης άσκησης ώστε να παίρνει υπόψη-του και την y-συντεταγμένη. Δηλαδή: αν το x είναι άρτιος, τότε αν το y είναι άρτιος, τότε κόκκινος κύκλος, αλλιώς μπλε· αλλιώς (με x περιττό) τότε αν y άρτιος τότε πράσινος, αλλιώς κίτρινος. Και εδώ θα βλέπετε κύκλους “τυχαίων” χρωμάτων όταν εκτελείτε το πρόγραμμά σας.

1.3 Η επανάληψη (ή ανακύκλωση)

Οι μαγειρικές συνταγές συνήθως δεν περιλαμβάνουν αυτή τη δομή· ή όταν την περιλαμβάνουν το κάνουν πολύ έμμεσα, όπως π.χ. όταν λένε: «Περιμένουμε μέχρι να φουσκώσει η ζύμη.» Που σημαίνει οτι όσο δεν έχει φουσκώσει ακόμα η ζύμη, εμείς κάνουμε κάτι άλλο· π.χ. διαβάζουμε ένα βιβλίο, βλέπουμε τηλεόραση, κλπ. Επαναλαμβάνουμε επομένως κάποιες ασχολίες ώσπου να συμβεί κάποιο γεγονός το οποίο ελέγχουμε. Άρα υπάρχει ένας λογικός έλεγχος (το αν φούσκωσε η ζύμη στο παράδειγμά μας), όπως και μια ακολουθία εντολών που επαναλαμβάνονται. Ας κάνουμε τώρα πιο συγκεκριμένα τα παραπάνω με ένα προγραμματιστικό παράδειγμα.

Θα ζωγραφίσουμε μια σειρά από κύκλους, π.χ. 10 στον αριθμό, αλλά “αυτόματα”, χωρίς δηλαδή να κάνουμε κλικ στην οθόνη. Ο κάθε κύκλος θα έχει διαφορετικό χρώμα, που θα αλλάζει από κόκκινο σε ιώδες περνώντας από ενδιάμεσα χρώματα της ίριδας. Ορίστε πρώτα το αποτέλεσμα του προγράμματος που θα φτιάξουμε, ώστε να έχουμε μια οπτική αντίληψη του τί προσπαθούμε να πετύχουμε:

Εννοείται οτι δεν έχει νόημα να γράψουμε 10 εντολές που η κάθε μία να ζωγραφίζει έναν κύκλο με διαφορετικό χρώμα, γιατί στο κάτω-κάτω το πρόβλημα μπορεί να μας ζητούσε να ζωγραφίσουμε 100 τέτοιους κύκλους (μικρούς, για να χωράνε), ή 1000, κλπ. Πρέπει να μπορούμε να πετύχουμε “αυτόματα”, ή “με τη μία” το ζωγράφισμα όλων των κύκλων, και αυτό γίνεται με την επανάληψη ή ανακύκλωση (αγγλ.: loop).

1.3.1 Η ανακύκλωση με το while

Για να κάνουμε τη σύνδεση με τα όσα είπαμε περί συνταγής, παραπάνω, ο αλγόριθμος της επανάληψης που θέλουμε να κάνουμε πρέπει να είναι ο εξής:

Τον παραπάνω αλγόριθμο θα υλοποιήσουμε με κώδικα που θα γράψουμε στη μέθοδο paint (όπως στο παράδειγμα της ακολουθίας ενολών), και όχι στη mouseReleased, γιατί θυμίζουμε οτι θέλουμε οι κύκλοι να εμφανίζονται με το που εκτελείται το πρόγραμμα, και όχι μετά από κλικ στην οθόνη. Γράφουμε λοιπόν την paint ως εξής:

public void paint (Graphics g) {
   int width = getBounds().width;
   int height = getBounds().height;
   if ( ! screenPainted) {
      screenPainted = true;
      // Code specifying what must happen only once (i.e., initializations)
      // when the window of the program has just opened, goes here.
   }
   int i = 0;
   while (i < 10) {
      Circle circle = new Circle (100 + (i * 80), height/2, 40);
      circle.Paint (g, null, Color.getHSBColor ((float) (i * 0.1), (float) 1.0, (float) 1.0));
      i = i + 1;
   }
}

Η εξήγηση των παραπάνω εντολών, από την int i = 0 και μετά, είναι η εξής:

Άσκηση 1.5: Πειραματιστείτε με τις αριθμητικές παραμέτρους του προγράμματος ως εξής:

Ορίστε το αποτέλεσμα της άσκησης μετά το τελευταίο βήμα:

1.3.2 Η ανακύκλωση με το for

Θα προχωρήσουμε τώρα σε μια συντακτικά εναλλακτική μορφή ανακύκλωσης, την ανακύκλωση for. “Συντακτικά εναλλακτική” σημαίνει οτι ότι μπορούμε να γράψουμε μέσω της δομής while, μπορούμε να το γράψουμε και μέσω της δομής for. Μπορούμε επίσης να πούμε οτι οι δύο δομές (while και for) είναι “συντακτικά ισοδύναμες”. Ιδού τί σημαίνει αυτό:

είναι ισοδύναμος (δηλαδή έχει το ίδιο αποτέλεσμα) με τον κώδικα:

που όπως παρατηρούμε είναι πιο σύντομος. Η αρχικοποίηση του μετρητή (i), ο έλεγχος για το σταμάτημα της ανακύκλωσης (i < 10), αλλά και η αύξηση του μετρητή κατά 1 (i ++), έχουν όλα τοποθετηθεί σε μία γραμμή, μέσα στην παρένθεση της ανακύκλωσης for. Το “νόημα” του παραπάνω κώδικα γίνεται εύκολα αντιληπτό: «Επανάλαβε τα όσα είναι μέσα σε άγκιστρα ([...]) 10 φορές». Αντίθετα, όταν χρησιμοποιούμε τη δομή while η αρχικοποίηση του μετρητή και ιδίως η αύξησή του κατά 1 μπορεί να απέχουν αρκετά από το while, πράγμα που κάνει τον κώδικά μας λιγότερο εύκολα αναγνώσιμο. Αυτό δεν σημαίνει οτι πρέπει να χρησιμοποιούμε την ανακύκλωση for πάντα· υπάρχουν και περιπτώσεις όπου η δομή while ενδείκνυται περισσότερο — το ποιες είναι αυτές θα μας το διδάξει η πείρα. Πάντως η αλήθεια είναι οτι στη μεγάλη πλειοψηφία των περιπτώσεων η δομή for μοιάζει πιο βολική.

Το πρόγραμμα με τους κύκλους, επομένως, γράφεται πιο σύντομα και ως εξής:

for (int i = 0;  i < 10;  i ++) {
   Circle circle = new Circle (100 + (i * 80), height/2, 40);
   circle.Paint (g, null, Color.getHSBColor ((float) (i * 0.1), (float) 1.0, (float) 1.0));
}

Άσκηση 1.6: Δείτε πάλι τον κώδικα που γράψατε για το τελευταίο (τέταρτο) μέρος της προηγούμενης άσκησης, και μετατρέψτε-το ώστε να χρησιμοποιεί τη δομή for για την ανακύκλωση.

Διπλή, ή πολλαπλή ανακύκλωση

Θέλουμε τώρα να γράψουμε ένα πρόγραμμα που να παράγει την ακόλουθη εικόνα:

Στην εικόνα αυτή, οι κύκλοι είναι διαρρυθμισμένοι σε δύο διαστάσεις, αφού η συνολική εικόνα των κύκλων είναι ένα ορθογώνιο με πλάτος και ύψος. Για να παραχθεί αυτή η διαρρύθμιση των κύκλων χρησιμοποιούμε μια διπλή ανακύκλωση. Δηλαδή κλείνουμε την οικεία-μας ανακύκλωση που παράγει μια σειρά από κύκλους μέσα σε μια άλλη, “εξωτερική” ανακύκλωση, που παράγει τις 10 σειρές. Ιδού ο κώδικας:

int hue = 0;
for (int j = 0;  j < 10;  j ++) {
   for (int i = 0;  i < 20;  i ++) {
      Circle circle = new Circle (100 + (i * 40), 50 + (j * 40), 20);
      circle.Paint (g, null, Color.getHSBColor ((float) (hue * 0.023), (float) 1.0, (float) 1.0));
      hue ++;
   }
}

Χρησιμοποιήθηκε η μεταβλητή hue όχι για κανέναν άλλο λόγο αλλά απλώς για να μετατοπίζεται το χρώμα των κύκλων κατά μία τιμή που επιτρέπει να ξεκινάει η κάθε σειρά με διαφορετικό χρώμα. (Αυτό γίνεται με το γινόμενο hue * 0.023, καθώς το 0.023 είναι ένας σχεδόν “τυχαίος” αριθμός.) Θα μπορούσαμε να χρησιμοποιήσουμε και το i, αλλά τότε όλες οι σειρές θα ήσαν πανομοιότυπες.

Το “δίδαγμα” που πρέπει να αποκομίσουμε από τα παραπάνω είναι οτι όταν αυτό που θέλουμε να κάνουμε (να εμφανίσουμε, να υπολογίσουμε) είναι δύο διαστάσεων, τότε χρησιμοποιούμε δύο ανακυκλώσεις, φωλιασμένες η μία μέσα στην άλλη. Αν έχουμε να κάνουμε με τρεις διαστάσεις, τότε χρησιμοποιούμε τρεις φωλιασμένες ανακυκλώσεις, κ.ο.κ.

1.3.3 Η τρίτη (και τελευταία) δομή ανακύκλωσης: η do – while

Υπάρχει και μια τρίτη προγραμματιστική δομή ανακύκλωσης: η do – while, που όμως δεν είναι ισοδύναμη με τις προηγούμενες δύο (while και for), και για το λόγο αυτό χρησιμοποιείται σπάνια. Το συντακτικό-της είναι το εξής:

Η διαφορά εδώ είναι οτι οι εντολές που βρίσκονται στην παραπάνω ανακύκλωση (αυτά που αντιπροσωπεύουν οι τρεις τελείες [...]) εκτελούνται τουλάχιστον μία φορά. Αντίθετα, οι προηγούμενες δύο ανακυκλώσεις (while και for) μπορούν να και να μην εκτελέσουν τις εντολές-τους καθόλου (δηλ. να τις εκτελέσουν “0 φορές”), αφού το λογικό έλεγχο της εξόδου από την ανακύκλωση τον εκτελούν αμέσως με το που ξεκινούν· ενώ η do – while ελέγχει για έξοδο στο τέλος-της. Η πιο συνηθισμένη κατάσταση στον προγραμματισμό είναι να είναι δυνατό να εκτελεστεί και “0 φορές” η ανακύκλωση, εξ ου και η σπανιότητα χρήσης της do – while.

1.4 Μεταβλητές, σταθερές, και τύποι-τους

Μέχρι το σημείο αυτό κάναμε χρήση κάποιων εννοιών χωρίς να τις εξηγήσουμε. Αυτό έγινε προκειμένου να προχωρήσουμε με μεγάλα βήματα στην εξοικείωση με την έννοια του προγράμματος. Τώρα όμως πρέπει να κάνουμε πιο συγκεκριμένο αυτό του οποίου κάναμε άφθονη χρήση μέχρι στιγμής. Πρόκειται για τις έννοιες “μεταβλητή” και “σταθερά”.

Μεταβλητές χρησιμοποιήσαμε όταν γράψαμε λέξεις όπως i, j, x, hue, width, height, κλπ.

Σταθερές χρησιμοποιήσαμε όταν γράψαμε αριθμούς όπως 0, 10, 0.023, όπως και όταν γράψαμε τη λέξη null.

Οι μεταβλητές λέγονται έτσι γιατί οι τιμές-τους μεταβάλλονται. Π.χ. αρχικοποιούμε τη μεταβλητή i με την τιμή 0 (μια σταθερά), και στη συνέχεια τη μεταβάλλουμε, αυξάνοντάς την κατά 1.

Αντίθετα, οι σταθερές λέγονται έτσι γιατί παραμένουν αμετάβλητες. Π.χ. το 10 δεν πρόκειται ποτέ να αλλάξει· θα έχει την τιμή 10 μόνιμα στο πρόγραμμά μας.

Υπάρχουν διάφοροι τύποι μεταβλητών και σταθερών. Ο τύπος που χρησιμοποιήσαμε σχεδόν παντού παραπάνω ήταν αυτός των ακέραιων αριθμών (integers). Δηλαδή είδαμε μεταβλητές που παίρνουν σαν τιμές ακέραιους αριθμούς, και τις ορίσαμε με το σύμβολο int. Οι ακέραιοι αριθμοί είναι οι θετικοί 1, 2, 3,... ο 0, και οι αρνητικοί –1, –2, –3,.... Φυσικά, όταν γράφουμε 0, 1, 2, κλπ., αυτές είναι σταθερές ακέραιων αριθμών. Υπάρχουν όμως και άλλοι τύποι, όπως ο τύπος των πραγματικών αριθμών (double), που είναι όσοι αριθμοί έχουν υποδιαστολή (την τελεία), όπως το 0.023 που χρησιμοποιήσαμε· ο τύπος των χαρακτήρων (char), που είναι γράμματα (συνήθως τα βλέπουμε στο πληκτρολόγιο) που κλείνουμε ανάμεσα σε απλά εισαγωγικά, έτσι: 'A', 'B', '+', '=', '4', 'Φ', 'a', 'β', ' ', κλπ.· ο τύπος της ακολουθίας γραμμάτων, ή String, όπως θα τον ονομάζουμε, που είναι χαρακτήρες — όχι μόνο ένας αλλά οσοιδήποτε στον αριθμό — που τους κλείνουμε σε διπλά εισαγωγικά, έτσι: "hello", "kalimera", "καλημέρα", "A", "", κλπ. (το τελευταίο String δεν έχει κανένα χαρακτήρα)· και ο τύπος των λογικών τιμών, ή boolean, που παίρνει δύο μόνο τιμές, τις σταθερές true και false. Όλα αυτά θα τα δούμε με λεπτομέρειες στην πράξη.

Εδώ σταματάμε προσωρινά τα εισαγωγικά θέματα. Υπάρχουν περισσότερα να πούμε, όμως τα βασικά έχουν ήδη καλυφθεί, και αυτό που προέχει τώρα είναι να χρησιμοποιήσουμε αυτές τις γνώσεις για να μπούμε στην ουσία, στην “καρδιά” του προγραμματισμού, που είναι η επινόηση αλγορίθμων. Η φράση “φτιάχνω πρόγραμμα” σημαίνει οτι “επινοώ έναν αλγόριθμο που λύνει το πρόβλημα” αρχικά, και στη συνέχεια γράφω τον κώδικα του προγράμματος.

2. Αλγόριθμοι

Θα αφήσουμε τώρα λίγο τη ζωγραφική των κύκλων κατά μέρος, για να περάσουμε στην αριθμητική, και συγκεκριμένα στον τομέα της αριθμοθεωρίας. (Αν και, μετά από λίγο, τα ευρήματά μας πάλι μέσω έγχρωμων κύκλων θα τα εμφανίζουμε.)

Ένας αριθμός x λέγεται διαιρέτης ενός άλλου αριθμού y όταν ο y διαιρείται ακριβώς από τον x χωρίς η διαίρεση να αφήνει υπόλοιπο.

Παραδείγματος χάρη, ο 3 είναι διαιρέτης του 12, γιατί 12 / 3 κάνει ακριβώς 4, χωρίς υπόλοιπο (ή με υπόλοιπο 0). Το ίδιο και ο 6: είναι επίσης διαιρέτης του 12. Αντίθετα, ο 8 δεν είναι διαιρέτης του 12, γιατί 12 / 8 δίνει πηλίκο 1 και υπόλοιπο 4.

Απάντηση: Ξεκινάμε και εξετάζουμε όλους τους αριθμούς που είναι μικρότεροι από το 36, και όποιον βρίσκουμε οτι διαιρεί ακριβώς το 36 (δηλ. οτι είναι διαιρέτης του 36) τον εμφανίζουμε στην οθόνη-μας.

Αυτό που δίνει η παραπάνω απάντηση είναι ένας αλγόριθμος, μια “προγραμματιστική συνταγή”. Ας γράψουμε ένα πρόγραμμα που να υλοποιεί τον παραπάνω αλγόριθμο. (Μπορούμε να το γράψουμε μέσα στην paint της AppPanel.)

Η συνταγή μας λέει να γράψουμε μια ανακύκλωση, από το 1 μέχρι το 36:

(Ο αναγνώστης θα πρόσεξε οτι τώρα δεν ξεκινήσαμε από το 0, γιατί γνωρίζουμε οτι το μηδέν δεν είναι διαιρέτης κανενός αριθμού· αυτό ισχύει γιατί απαγορεύεται να διαιρέσουμε έναν αριθμό διά του μηδενός.)

Στη συνέχεια, μέσα στην ανακύκλωση, πρέπει να εξετάζουμε αν το i διαιρεί το 36, και αν ναι, τότε να εμφανίζουμε το i. Πρέπει να προνοήσουμε όμως για το πού θα το εμφανίζουμε. Αυτό θα το κάνουμε μέσω μιας μεταβλητής x, που θα δίνει τη x-συντεταγμένη του σημείου της οθόνης όπου θα εμφανίζουμε τον αριθμό, ενώ η y-συντεταγμένη θα είναι σταθερή, και ίση π.χ. με 50. Ιδού:

Όταν λοιπόν το i είναι διαιρέτης του 36 (αυτό λέει ο λογικός έλεγχος if (36 % i == 0)) τότε εμφανίζουμε το i στην οθόνη (μέσω του g.drawString ("" + i) στις συντεταγμένες x, 50. Αμέσως στη συνέχεια προνοούμε να αυξήσουμε το x κατά 40 pixels οθόνης, ώστε το επόμενο i (αν υπάρξει) να εμφανιστεί πιο δεξιά. Το παραπάνω πρόγραμμα παράγει το εξής αποτέλεσμα (άνω μέρος οθόνης):

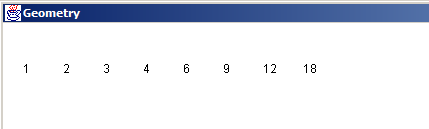
Ερώτηση 2.2: Είναι απαραίτητο η ανακύκλωσή μας να φτάνει μέχρι το 36; Αν ξεπεράσουμε το 18 έχουμε καμιά ελπίδα να βρούμε ποτέ κάποιον ακόμα διαιρέτη;

Η απάντηση είναι προφανώς όχι. Αν ξεπεράσουμε το μισό του αριθμού του οποίου ψάχνουμε τους διαιρέτες, προφανώς δεν πρόκειται να βρούμε άλλους από ’κεί και πέρα.

Άσκηση 2.1: Τροποποιήστε το παραπάνω πρόγραμμα ώστε η ανακύκλωση να φτάνει μόνο μέχρι το μισό του αριθμού. Επίσης, αντί να χρησιμοποιείτε σταθερές όπως 36 και 18, χρησιμοποιήστε μια μεταβλητή Ν, στην οποία θα δώσετε αρχικά την τιμή 36, και από ’κεί και πέρα το πρόγραμμα θα πρέπει να αναφέρεται μόνο στο Ν, και όχι στο 36 ή στο 18. Επίσης, πολύ σημαντικό για τη συνέχεια (να υλοποιηθεί οπωσδήποτε, παρόλο που είναι απλούστατο): κάντε το πρόγραμμα να μην ξεκινάει από τον αριθμό 1 αλλά από το 2, αφού γνωρίζουμε οτι ο 1 είναι διαιρέτης κάθε αριθμού, άρα δεν χρειαζόμαστε να τον βλέπουμε.

Άσκηση 2.2: Δώστε διαφορετικές τιμές στο Ν, όπως 30, 60, και 61 και τρέξτε το πρόγραμμα. Τί παρατηρείτε στην περίπτωση του 61;

Άσκηση 2.3: Θέλουμε τώρα να μετράμε τον αριθμό των διαιρετών ενός αριθμού, και να εμφανίζουμε αυτόν τον αριθμό, και όχι τους διαιρέτες έναν-έναν. Π.χ. για τον 12 θα πρέπει να εμφανιστεί ο αριθμός 4, αφού ο 12 έχει 4 διαιρέτες: τους 2, 3, 4, και 6. (Είπαμε οτι με τον 1 δεν θα ασχοληθούμε από ’δώ και στο εξής.) Για τον 7 θα πρέπει να εμφανιστεί ο αριθμός 0, αφού ο 7 δεν έχει κανένα διαιρέτη. Γράψτε το πρόγραμμα.

Άσκηση 2.4: Αντί να εμφανίζουμε τον αριθμό των διαιρετών, θα εμφανίζουμε τώρα μια στήλη από κόκκινους κύκλους, εφαπτόμενους (τον έναν πάνω στον άλλο), τόσους όσοι οι διαιρέτες του αριθμού. Ιδού ένα παράδειγμα για τον αριθμό 30, που έχει 6 διαιρέτες:

Αφού υλοποιήσετε την άσκηση 2.4, βεβαιωθείτε οτι για τους αριθμούς 7, 23, και 61 (μεταξύ άλλων) το πρόγραμμα δεν ζωγραφίζει κανέναν κύκλο.

Αυτούς τους αριθμούς για τους οποίους το πρόγραμμα της άσκησης 2.4 δεν εμφανίζει κανέναν κύκλο τους ονομάζουμε “πρώτους”. Με άλλα λόγια, πρώτοι αριθμοί είναι όσοι δεν έχουν κανέναν “κανονικό” διαιρέτη (δηλαδή κάποιο διαιρέτη διαφορετικό από τους δύο τετριμμένους, που είναι η μονάδα και ο “εαυτός”, δηλ. ο ίδιος ο αριθμός). Οι πρώτοι αριθμοί παίζουν πρωταγωνιστικό ρόλο στη λεγόμενη “θεωρία αριθμών”. Εδώ όμως θα τους χρησιμοποιήσουμε απλώς για να εξασκηθούμε στην κατασκευή αλγορίθμων.

Άσκηση 2.5: Επεκτείνετε τώρα την άσκηση 2.4 ως εξής: κάντε κάθε αριθμό από το 2 ως το 100 να εμφανίζει τόσους κύκλους όσοι οι διαιρέτες-του, όπως στην άσκηση 2.4. Βάλτε τους 99 αριθμούς με τη σειρά τον ένα μετά τον άλλον, όπως στην παρακάτω εικόνα. Πρέπει βέβαια να μικρύνετε πολύ τη διάμετρο των κύκλων ώστε να χωρέσουν όλοι. (Στην εικόνα, οι κύκλοι έχουν διάμετρο 8.)

Οι πρώτοι αριθμοί, στην παραπάνω εικόνα, βρίσκονται εκεί που υπάρχουν κενά. Ο πρώτος (απομονωμένος) κύκλος στα αριστερά της εικόνας αντιστοιχεί στον αριθμό 4, που έχει ένα διαιρέτη. Αριστερά-του υπάρχουν δύο ακόμα κενά, που βέβαια δεν φαίνονται, και αντιστοιχούν στους αριθμούς 2 και 3, που είναι πρώτοι. Δεξιά του 4 υπάρχει ένα κενό για τον αριθμό 5 που είναι πρώτος, ακολουθεί ο αριθμός 6 με δύο διαιρέτες (τα 2 & 3), κενό για τον αριθμό 7 (πρώτος), κ.ο.κ.

Άσκηση 2.6: Κάντε τώρα να εμφανίζεται ένας μπλε κύκλος στη θέση των πρώτων αριθμών της άσκησης 2.5. Εκεί δηλαδή όπου οι αριθμοί δεν είναι πρώτοι, να εμφανίζονται οι κόκκινοι κύκλοι ακριβώς όπως στην άσκηση 2.5· αλλά εκεί όπου υπάρχουν πρώτοι να εμφανίζεται ακριβώς ένας μπλε κύκλος, όπως στην παρακάτω εικόνα.

2.1 Μέθοδοι

Μέχρι αυτό το σημείο, όποτε θελήσαμε να γράψουμε κώδικα προγράμματος, τον προσθέσαμε σε κάποιο ειδικό σημείο της τάξης AppPanel, όπως η paint, η mouseReleased, κλπ., οι οποίες όπως είπαμε λέγονται μέθοδοι της τάξης AppPanel. Μπορούμε όμως να φτιάξουμε και δικές-μας μεθόδους, τις οποίες θα προσθέσουμε στο πρόγραμμά μας. Μάλιστα, όπως θα μάθουμε, ο προγραμματισμός είναι μια διαδικασία κατά την οποία διαρκώς προσθέτουμε νέες μεθόδους στο πρόγραμμά μας, τροποποιούμε τις παλιές, κλπ.

Ένας από τους λόγους για τον οποίο προσθέτουμε μεθόδους είναι για να τμηματοποιούμε το πρόγραμμά μας σε κομμάτια τα οποία μπορούμε εύκολα να αναγνωρίσουμε. Όπως ένα βιβλίο αποτελείται από κεφάλαια, όπου το κάθε κεφάλαιο έχει έναν τίτλο, έτσι και το πρόγραμμά μας — και συγκεκριμένα η κάθε τάξη-του, όπως η AppPanel — αποτελείται από μεθόδους, όπου η κάθε μέθοδος έχει ένα όνομα. Ας φανταστούμε πόσο βαρετό και δύσκολο στην ανάγνωση θα ήταν ένα βιβλίο μερικών εκατοντάδων σελίδων που δεν είναι χωρισμένο σε κεφάλαια. Το ίδιο ακριβώς θα συνέβαινε αν δεν χωρίζαμε το πρόγραμμά μας στις λογικές-του ενότητες, δηλαδή σε μεθόδους. Λέμε οτι μια μέθοδος πρέπει να αποτελεί “μία λογική ενότητα” γιατί πρέπει να ασχολείται με ένα πράγμα, μία ιδέα· αν μια μέθοδος ασχολείται με περισσότερες από μια ιδέες, τότε μάλλον πρέπει να τη διαμερίσουμε σε άλλες, περισσότερες μεθόδους.

Ένας άλλος λόγος είναι οτι μέσω των μεθόδων αποφεύγουμε να επαναλαμβάνουμε τις ίδιες γραμμές κώδικα στο πρόγραμμά μας. Το τί σημαίνει αυτό θα το καταλάβουμε σύντομα. Προς το παρόν, ας φτιάξουμε την πρώτη δική-μας μέθοδο. Προς το σκοπό αυτό θα κάνουμε τα εξής βήματα:

Βήμα 1. Θα πάμε ακριβώς πριν από τη μέθοδο paint της τάξης AppPanel, και θα προσθέσουμε τα εξής:

Τις τρεις τελείες δεν χρειάζεται να τις γράψουμε· τοποθετήθηκαν εκεί για να γίνει κατανοητό σε ποιο σημείο της νέας-μας μεθόδου (που λέγεται PaintPrimesInBlue) θα εισάγουμε τις γραμμές κώδικα που εξηγεί το επόμενο βήμα.

Βήμα 2. Θα πάρουμε τώρα όλες τις γραμμές κώδικα που έχουμε προσθέσει μέσω και της τελευταίας άσκησης (2.6) στη μέθοδο paint της τάξης AppPanel, δηλαδή θα τις επιλέξουμε, θα τις κάνουμε “αποκοπή” (π.χ. με Ctrl-X), και μετά θα τις “επικολλήσουμε” (π.χ. με Ctrl-V) στη θέση των τριών τελειών της νέας-μας μεθόδου PaintPrimesInBlue.

Βήμα 3. Τέλος, στο σημείο της paint της τάξης AppPanel απ’ όπου κάναμε την αποκοπή των γραμμών του κώδικα, θα γράψουμε μία μόνο γραμμή, την εξής:

Έτσι, ουσιαστικά αντικαταστήσαμε τις γραμμές εκείνες της paint με μία μόνο, την παραπάνω γραμμή. Όταν το πρόγραμμά μας φτάνει σ’ αυτή τη γραμμή της paint, τότε “μπαίνει μέσα” στην (ή καλεί, όπως λέμε, την) PaintPrimesInBlue, εκτελεί τις εντολές-της, και όταν τελειώσει επανέρχεται πίσω στην paint, και συνεχίζει από το σημείο της κλήσης της PaintPrimesInBlue και μετά. Το πώς ακριβώς “κινείται” ο έλεγχος του προγράμματος από τη μια μέθοδο στην άλλη γίνεται κατανοητό με τη χρήση του debugger, όπως εξηγείται στις παραδόσεις του μαθήματος.

2.1.1 Οι χαρακτηρισμοί private και public

Ο αναγνώστης μπορεί να παρατήρησε οτι στον ορισμό της μεθόδου PaintPrimesInBlue, παραπάνω, γράψαμε στην πρώτη-της σειρά τον χαρακτηρισμό της μεθόδου σαν private:

Άλλες όμως μέθοδοι, που προϋπήρχαν στην AppPanel, όπως η paint, έχουν το χαρακτηρισμό public:

Η διαφορά του να χαρακτηρίζουμε μια μέθοδο σαν public ή σαν private είναι η εξής: όταν μια μέθοδος είναι public, ήτοι “δημόσια”, τότε είναι “ορατή απ’ έξω από την τάξη-της”. Δηλαδή οποιαδήποτε άλλη τάξη εκτός της AppPanel μπορεί να “δει” τη δημόσια μέθοδο και να τη χρησιμοποιήσει. Αυτό γίνεται ως εξής: αν μια άλλη τάξη έχει ένα αντικείμενο που λέγεται π.χ. appPanel και είναι τάξης AppPanel, τότε η άλλη αυτή τάξη μπορεί να πει: appPanel.paint(g). Αντίθετα, όταν μια μέθοδος είναι private, ήτοι “ιδιωτική”, τότε παραμένει “αόρατη”, κρυμμένη από άλλες τάξεις, και μπορεί να χρησιμοποιηθεί μόνο εντός της τάξης στην οποία ανήκει — στο παράδειγμά μας εντός της AppPanel. Πράγματι, βλέπουμε παραπάνω οτι την ιδιωτική μέθοδο PaintPrimesInBlue τη χρησιμοποιούμε (την καλούμε) μόνο μέσα στην AppPanel, και συγκεκριμένα στη μέθοδο paint.

Ο λόγος που ορίζουμε μια μέθοδο σαν public ή σαν private είναι οτι κάθε τάξη πρέπει να κρατάει σαν ιδιωτικό (private), κρυφό από τον “έξω κόσμο” (δηλ. τον “κόσμο” των υπόλοιπων τάξεων), όσο πιο πολύ από τον κώδικά της γίνεται· και αντίστοιχα, να επιτρέπει στον “έξω κόσμο” να βλέπει όσο πιο λίγες από τις εσωτερικές λειτουργίες-της γίνονται. Αυτό το επιθυμούμε χάριν απλότητας. Όταν βρισκόμαστε στον “έξω κόσμο” και θέλουμε να χρησιμοποιήσουμε την τάξη, αυτό που μας απασχολεί είναι το τί κάνει η τάξη αυτή, όχι το πώς το κάνει. Επομένως το πώς το κάνει το κρύβουμε όσο μπορούμε σε ιδιωτικές μεθόδους, ενώ το τί το αφήνουμε να γίνεται ορατό μέσω των δημόσιων μεθόδων.

2.1.2 Ο χαρακτηρισμός void

Μετά από τον χαρακτηρισμό private, στην πρώτη γραμμή ορισμού της νέας-μας μεθόδου PaintPrimesInBlue υπάρχει ο χαρακτηρισμός void. Η έννοια αυτού του χαρακτηρισμού είναι οτι “αυτή η μέθοδος δεν επιστρέφει τίποτα”. Πιο γενικά, αντί του void μπορούμε στο σημείο εκείνο να βάλουμε έναν “τύπο δεδομένων”, όπως οι int, double, char, και boolean, που συναντήσαμε στην §1.4· ή ακόμα μπορεί να είναι το όνομα μιας οποιασδήποτε τάξης, όπως η String (που και πάλι αναφέρθηκε στην §1.4), η Circle, κλπ. Το ποιος είναι ο τύπος δεδομένων εξαρτάται από το τί είδους είναι η οντότητα (ο αριθμός, το αντικείμενο) που επιστρέφει η μέθοδος σε όποιον την κάλεσε: αν είναι ακέραιος αριθμός γράφουμε int· αν είναι ολόκληρη φράση γράφουμε String· κ.ο.κ. Στην περίπτωσή μας, επειδή η μέθοδός μας δεν επιστρέφει τίποτα (αλλά απλώς κάνει κάτι το ορατό στην οθόνη), γράφουμε void. Σύντομα (αρχίζοντας από την §2.1.4) θα συναντήσουμε άλλες μεθόδους που θα επιστρέφουν κάποιον αριθμό, ή κάποιο αντικείμενο, σε όποιον τις κάλεσε.

2.1.3 Η παρένθεση με τις παραμέτρους

Μετά από το όνομα της μεθόδου PaintPrimesInBlue ακολουθεί ένα ζευγάρι παρενθέσεων, όπου μέσα-τους γράφουμε τις παραμέτρους της μεθόδου. Το τί είναι οι παράμετροι θα το καταλάβουμε σε επόμενα παραδείγματα, όταν θα δούμε μεθόδους που χρησιμοποιούν παραμέτρους που είναι πιο “χρήσιμες” από αυτήν που βλέπουμε στην PaintPrimesInBlue. Εδώ βλέπουμε οτι χρησιμοποιείται η παράμετρος g, που είναι τύπου Graphics, γιαυτό γράφουμε Graphics g. Η εξήγηση για τη χρησιμότητα των παραμέτρων δίνεται στην αμέσως επόμενη υποενότητα, 2.1.4, και περαιτέρω συζήτηση γίνεται στην υποενότητα 2.1.5.

2.1.4 Μία νέα μέθοδος με επιστροφή τιμής και παράμετρο

Θα επαναλάβουμε τώρα την προηγούμενη διαδικασία δημιουργίας μεθόδου, παίρνοντας ένα τμήμα της μεθόδου PaintPrimesInBlue και δημιουργώντας μία νέα μέθοδο με αυτό. Συγκεκριμένα, θα πάμε στο σημείο πριν από την PaintPrimesInBlue και θα προσθέσουμε τον ορισμό της νέας μεθόδου NumberOfDivisors, που θα μας υπολογίζει τον αριθμό των διαιρετών ενός αριθμού:

Όπως και πρωτύτερα, τις τρεις τελείες θα τις αντικαταστήσουμε με ένα τμήμα κώδικα, το οποίο θα αφαιρέσουμε από τη μέθοδο PaintPrimesInBlue (με αποκοπή). Το τμήμα αυτό είναι οι παρακάτω γραμμές, που υπολογίζουν ακριβώς αυτό που θέλουμε, δηλαδή τον αριθμό των διαιρετών του αριθμού Ν:

Τις γραμμές αυτές θα τις επικολλήσουμε στη θέση των τριών τελειών της NumberOfDivisors, και από κάτω-τους (πριν βέβαια από το άγκιστρο } που κλείνει τη μέθοδο) θα προσθέσουμε την εξής γραμμή:

Τέλος, στο σημείο της PaintPrimesInBlue απ’ όπου αποκόψαμε τις παραπάνω γραμμές θα γράψουμε την εξής μία γραμμή:

Ας δούμε τώρα ολόκληρη τη νέα μέθοδο NumberOfDivisors, με τη σωστή “παραγραφοποίηση” (εισαγωγή κενών στα αριστερά κάθε γραμμής):

Στην πρώτη γραμμή, που λέγεται και “κεφαλή” (“header”) της μεθόδου, μετά από το χαρακτηρισμό private (που εξηγήθηκε στην §2.1.1) υπάρχει ο χαρακτηρισμός int, που σημαίνει οτι αυτή η μέθοδος επιστρέφει μια ακέραια τιμή (βλ. §2.1.2). Το νόημα αυτής της τιμής είναι οτι θα πρόκειται για τον αριθμό των διαιρετών του ακέραιου αριθμού Ν, που δίνεται μέσα στην παρένθεση με τις παραμέτρους (int N). Πού όμως καθορίζεται αυτό το νόημα; Το νόημα καθορίζεται με τις επόμενες γραμμές που κλείνονται ανάμεσα σε άγκιστρα ({ και }) και αποτελούν το “σώμα” (“body”) της μεθόδου. Οι γραμμές του σώματος είναι οι οικείες-μας γραμμές από την προηγούμενη μέθοδο PaintPrimesInBlue — που ξέρουμε οτι μετρούν τους διαιρέτες του Ν και τον αριθμό-τους τον αποθηκεύουν στη μεταβλητή divisors — με μία επιπλέον γραμμή: την return divisors, που δίνει την εντολή στη νέα μέθοδο οτι «αυτή την τιμή, της μεταβλητής divisors, είναι που πρέπει να επιστρέψεις σε όποιον σε κάλεσε». Έτσι, “αυτός που καλεί” τη νέα-μας μέθοδο είναι η παλιά PaintPrimesInBlue, που το κάνει στη γραμμή int divisors = NumberOfDivisors (N), με την οποία αντικαταστήσαμε τον παλιό κώδικα.

Άσκηση 2.7: Ο αναγνώστης μπορεί να τοποθετήσει ένα breakpoint στη γραμμή int divisors = NumberOfDivisors (N), και να κάνει χρήση του debugger ώστε: 1. να σταματήσει στο breakpoint· 2. να κάνει step into, ώστε να βάλει τη ροή του προγράμματος στη μέθοδο NumberOfDivisors· 3. αφού εισέλθει στη NumberOfDivisors να εκτελέσει τις εντολές-της μία-μία για να δει πώς σχηματίζεται ο αριθμός των διαιρετών στη μεταβλητή divisors· και 4. αφού εκτελέσει και το άγκιστρο που κλείνει τη μέθοδο, να επιστρέψει στο σημείο απ’ όπου κλήθηκε η μέθοδος NumberOfDivisors, να κάνει ένα step over, και να εξετάσει την τιμή της μεταβλητής divisors στη μέθοδο PaintPrimesInBlue.

“Τοπικότητα” ονομάτων των παραμέτρων και μεταβλητών. Το όνομα της παραμέτρου της οποίας η NumberOfDivisors υπολογίζει τους διαιρέτες είναι Ν, γιατί έτσι λεγόταν ο αριθμός αυτός στην αρχική PaintPrimesInBlue. Σημαντικό όμως είναι να καταλάβουμε οτι το όνομα Ν είναι “τοπικό” στη NumberOfDivisors. Αυτό, μεταξύ άλλων, σημαίνει οτι μπορούμε και να το αλλάξουμε παντού όπου εμφανίζεται στη μέθοδο NumberOfDivisors, χωρίς καμία άλλη επίπτωση στο πρόγραμμά μας. Ορίστε η ίδια μέθοδος, όπου στο Ν έχουμε αλλάξει το όνομά του και το λέμε number:

Εννοείται οτι αντί για Ν ή number μπορούμε να δώσουμε οποιοδήποτε όνομα· πάντα όμως προτιμούμε να δίνουμε ονόματα που μας υπενθυμίζουν το ρόλο που παίζει η παράμετρος ή η μεταβλητή στο πρόγραμμα. (Αυτός άλλωστε είναι και ο λόγος που μέχρι τώρα χρησιμοποιήσαμε ονόματα όπως PaintPrimesInBlue, NumberOfDivisors, divisors, κλπ.)

Το οτι η παράμετρος είναι “τοπική” στη NumberOfDivisors σημαίνει επίσης οτι μπορούμε να της αλλάξουμε όχι μόνο το όνομα αλλά και την τιμή, χωρίς να επηρεαστεί η PaintPrimesInBlue που καλεί τη μέθοδο· αρκεί βέβαια αυτή η αλλαγή τιμής της παραμέτρου να μην αλλάζει τη σωστή λειτουργία της μεθόδου. Ένα σημείο στο οποίο μπορούμε να κάνουμε μια τέτοια — άνευ νοήματος όμως — αλλαγή της τιμής της παραμέτρου είναι ακριβώς πριν από την εντολή return divisors. Μπορούμε να γράψουμε πριν από αυτή τη γραμμή: number = 1234; (υποθέτοντας οτι τώρα η παράμετρος λέγεται number), οπότε καμία διαφορά δεν θα παρατηρήσουμε αν εκτελέσουμε το πρόγραμμα.

“Τοπική” στη NumberOfDivisors είναι επίσης η μεταβλητή divisors. Ισχύουν και γι’ αυτήν όσα είπαμε και για την παράμετρο, με τη διαφορά οτι αν της αλλάξουμε τιμή οπουδήποτε στη μέθοδο αυτή δεν θα υπολογίζουμε πλέον σωστά τους διαιρέτες της παραμέτρου.

Άλλη τοπική μεταβλητή είναι η i στο for loop. Αυτή μάλιστα είναι τοπική στο for! Το “εύρος”-της (“scope”) δηλαδή, όπως λέμε, είναι το for loop. Αν προσπαθήσουμε να τη χρησιμοποιήσουμε εκτός του εύρους-της (π.χ. αν πούμε return i αντί return divisors), θα διαμαρτυρηθεί ο μεταγλωττιστής, λέγοντάς μας οτι η μεταβλητή i είναι άγνωστη (στο σημείο του return).

Άσκηση 2.8: Ο αναγνώστης ας κάνει την αλλαγή της προηγούμενης παραγράφου για να δει το διαγνωστικό μήνυμα λάθους που δίνει ο μεταγλωττιστής. Αυτό μας δείχνει οτι ο μεταγλωττιστής είναι “κουτός”: δεν “αντιλαμβάνεται” οτι μ’ αυτό το i εμείς εννοούμε τη μεταβλητή του for loop. (Κακώς βέβαια την εννοούμε, γιατί δεν έχει νόημα η χρήση-της εκεί· αλλά θα μπορούσε και να έχει νόημα· και πάλι ο μεταγλωττιστής θα συμπεριφερόταν “κουτά”.) Ο αναγνώστης θα πρέπει να μην παραλείψει να επαναφέρει το αρχικό όνομα της παραμέτρου στην εντολή return.

Εύρος. Η έννοια του “εύρους” μεταβλητών και παραμέτρων, που αναφέρθηκε παραπάνω, είναι πολύ σημαντική και επεκτείνεται και στις μεθόδους. Π.χ., το εύρος των μεθόδων NumberOfDivisors και PaintPrimesInBlue, επειδή έχουν δηλωθεί σαν private, είναι μόνο η τάξη AppPanel. Αν είχαν δηλωθεί σαν public (όπως π.χ. είναι η paint) τότε το εύρος-τους θα ήταν ολόκληρη η εφαρμογή. Με άλλα λόγια, “εύρος” σημαίνει “πόσο μακριά, ή σε πόσο μεγάλο τμήμα του προγράμματος, είναι ορατό το αντικείμενο”, όπου “είναι ορατό” σημαίνει οτι “το αναγνωρίζει ο μεταγλωττιστής” (χωρίς να διαμαρτύρεται).

Συμφωνία τύπων. Άλλη μία σημαντική παρατήρηση με την εισαγωγή της μεθόδου NumberOfDivisors είναι η εξής: ο τύπος int που επιστρέφει η μέθοδος και που δηλώνεται στην κεφαλή της μεθόδου (πριν από το όνομά της) οφείλει να είναι πανομοιότυπος με τον τύπο αυτού που επιστρέφεται στην εντολή return (επίσης int, γιατί αυτός είναι ο τύπος της μεταβλητής divisors). Θα μπορούσε η εντολή return να επιστρέφει την παράσταση divisors-1 (λάθος, αλλά θα ήταν σωστό αν στον ορισμό της μεταβλητής divisors γράφαμε: int divisors = 1;)· κάτι τέτοιο θα διατηρούσε τον κανόνα περί συμφωνίας τύπων, γιατί και η παράσταση divisors-1 είναι τύπου int, καθώς και τα δύο “συστατικά”-της, δηλ. το divisors και το 1, είναι τύπου int, ενώ η αφαίρεση ενός ακεραίου από έναν άλλο δίνει φυσικά επίσης τύπο int. Βλέπουμε λοιπόν οτι τύπους μπορούν να έχουν και ολόκληρες παραστάσεις, όπως το divisors-1.

2.1.5 Περισσότερες από μία παράμετροι

Οι παράμετροι μέσα στις παρενθέσεις στην κεφαλή της μεθόδου μπορούν να είναι οσεσδήποτε στον αριθμό, αρκεί να διαχωρίζονται μεταξύ-τους με ένα κόμμα. Το παρακάτω παράδειγμα δείχνει την κεφαλή μιας μεθόδου με τρεις παραμέτρους: δύο ακέραιες, και μία λογική:

Εννοείται επίσης οτι ο τύπος της κάθε παραμέτρου δεν είναι απαραίτητο να είναι στοιχειώδης (int, boolean, double, κλπ.), αλλά μπορεί να είναι το όνομα μιας τάξης. Π.χ. στην §2.1.1 είδαμε οτι η μέθοδος PaintPrimesInBlue έχει μία παράμετρο, την g, τύπου Graphics, το οποίο είναι όνομα τάξης.

Άσκηση 2.9: Πρώτα, να γίνει αλλαγή του ονόματος της μεθόδου PaintPrimesInBlue, ώστε αυτή τώρα να λέγεται PaintPrimesInColor. Στη συνέχεια να προστεθούν δύο παράμετροι τύπου Color, από τις οποίες η πρώτη θα καθορίζει το χρώμα των κύκλων των πρώτων αριθμών, και η δεύτερη το χρώμα των μη-πρώτων αριθμών. Συγκεκριμένα, ορίστε η κεφαλή της μεθόδου:

Να τροποποιηθεί το σώμα της μεθόδου που τώρα ονομάζεται PaintPrimesInColor ώστε να εμφανίζει τη γνωστή ακολουθία πρώτων και μη-πρώτων αριθμών με διαφορετικό χρώμα. Παραδείγματος χάρη, καλώντας τώρα την PaintPrimesInColor εντός της paint με τον παρακάτω τρόπο,

πρέπει να πάρουμε την ακόλουθη εικόνα στην οθόνη-μας:

3. Δομές δεδομένων

Μέχρι τώρα γνωρίσαμε “απλούς” τύπους δεδομένων, και συγκεκριμένα τους εξής: int, float, double, char, και boolean. Υπάρχουν και σύνθετοι τύποι, που τους λέμε “δομές” δεδομένων. Από τις δομές δεδομένων θα μελετήσουμε εδώ μία μόνο, τους πίνακες, που είναι αρκετά απλή, ενώ πιο σύνθετες (οι “δυναμικές”) δομές δεδομένων είναι το αντικείμενο του ομώνυμου μαθήματος, Υ3. (Οι πίνακες δεν είναι “δυναμική” αλλά “στατική” δομή δεδομένων, που σημαίνει οτι το μέγεθός τους παραμένει σταθερό καθ’ όλη τη διάρκεια της εκτέλεσης του προγράμματος· αντίθετα, το μέγεθος των δυναμικών δομών αλλάζει την ώρα που εκτελείται το πρόγραμμα.) Επιπλέον, θα διαπιστώσουμε οτι και η έννοια της τάξης, που έχουμε συναντήσει σε ολόκληρο το μάθημα μέχρι τώρα, μπορεί κι αυτή να θεωρηθεί σαν ένα είδος δομής δεδομένων.

3.1 Πίνακες

Έστω οτι, αντί για τους κύκλους μέσω των οποίων μέχρι τώρα παριστάνουμε στην οθόνη τους πρώτους αριθμούς, θέλουμε να έχουμε μια λίστα, που να λέει “ναι” όταν ο αριθμός είναι πρώτος, και “όχι” όταν δεν είναι πρώτος. Η λίστα αυτή θα μοιάζει κάπως έτσι:

Επειδή όμως οι λέξεις “ναι” και “όχι” δεν είναι ο καλύτερος τρόπος να παριστάνουμε αυτό που θέλουμε από προγραμματιστική άποψη, θα αντικαταστήσουμε τις λέξεις αυτές με τις λογικές (boolean) τιμές true για το “ναι”, και false για το “όχι”. Έτσι, η λίστα θα μοιάζει με την παρακάτω:

Βέβαια θα υποθέσουμε οτι η λίστα έχει ένα τέλος, γιατί άπειρα (ατέρμονα) αντικείμενα δεν υπάρχουν στον προγραμματισμό. Ας πούμε λοιπόν οτι η λίστα-μας έχει 100 στοιχεία (όσα κ’ οι στήλες των πρώτων και σύνθετων αριθμών των προηγούμενων ενοτήτων). Όλες αυτές τις 100 τιμές τύπου boolean, δηλαδή τα 100 false ή true, θέλουμε να τα έχουμε σε ένα αντικείμενο, μία “δομή” όπως λέμε. Αυτό μπορούμε να το πετύχουμε δηλώνοντας έναν πίνακα τύπου boolean, ως εξής:

Οι αγκύλες, επομένως, που ακολουθούν τον απλό τύπο boolean, δηλώνουν οτι έχουμε να κάνουμε με έναν πίνακα (δηλαδή μια λίστα) από έναν αριθμό θέσεων τύπου boolean. Ολόκληρο τον πίνακα (τη λίστα) τον ονομάσαμε prime, επειδή θέλουμε να παριστάνει το αν μια θέση αυτού του πίνακα είναι πρώτος (prime) αριθμός ή όχι. (Θα μπορούσαμε φυσικά να του δώσουμε οποιοδήποτε όνομα, αλλά όπως πάντα προτιμούμε κάτι που να μας υπενθυμίζει για ποια δουλειά τον θέλουμε αυτόν τον πίνακα.)

Ακόμα όμως δεν έχουμε ορίσει οτι αυτός ο πίνακας έχει 100 θέσεις. Αυτό γίνεται ως εξής:

Τις δύο παραπάνω γραμμές μπορούμε να τις συγχωνεύσουμε σε μία (χάριν συντομίας και μόνο, αλλιώς το αποτέλεσμα είναι το ίδιο), ως εξής:

Τώρα ο πίνακας prime έχει δηλωθεί, και έχει 100 θέσεις, αλλά οι θέσεις-του είναι κενές, δεν έχουν ακόμα τις τιμές false ή true που θέλουμε να τους εκχωρήσουμε. Νά πώς μπορούμε να εκχωρήσουμε τιμές στις 100 θέσεις του πίνακα:

   for (int i = 0; i < 100; i ++)
      if (NumberOfDivisors (i) == 0)
         prime[i] = true;
      else
         prime[i] = false;

Αυτό που λέμε δηλαδή με τις παραπάνω γραμμές είναι: Για κάθε αριθμό (i) από το 0 μέχρι το 100, αν ο αριθμός των διαιρετών αυτού του αριθμού i είναι μηδέν (δηλ. αν ο i δεν έχει διαιρέτες, ήτοι αν είναι πρώτος), τότε βάλε την τιμή true στη θέση i του πίνακα prime· αλλιώς, στη θέση i βάλε την τιμή false.

Ένα ερώτημα είναι σε ποιο σημείο του προγράμματός μας θα μπορούσαν να γίνονται όλα αυτά. Δεν θέλουμε να προσθέσουμε τις παραπάνω γραμμές στην paint, όπως κάναμε μέχρι τώρα, γιατί η δουλειά αυτή είναι υπολογιστική, όχι “οπτική”, άρα δεν θέλουμε να υπολογίζονται οι θέσεις του πίνακα κάθε φορά που το πρόγραμμά μας ζωγραφίζει τα περιεχόμενα της οθόνης-του. (Γιατί όχι; Ας σκεφτούμε οτι μπορεί να θέλαμε ο πίνακάς μας να έχει όχι 100, αλλά ένα εκατομμύριο θέσεις, και ο υπολογισμός αυτών των 1.000.000 θέσεων μπορεί να παίρνει μερικά δευτερόλεπτα· αν λοιπόν τον κάνουμε να γίνεται εντός της paint, τότε το πρόγραμμά μας θα μοιάζει να “κολλάει” για μερικά δευτερόλεπτα κάθε φορά που χρειάζεται να ζωγραφίσει την οθόνη-του, γιατί θα υπολογίζει ξανά και ξανά τις θέσεις του τεράστιου πίνακά του.) Επομένως εδώ είναι η πρώτη φορά που θα διαχωρίσουμε τον υπολογισμό από την εμφάνιση των αποτελεσμάτων στην οθόνη. Αυτό μπορούμε να το πετύχουμε ως εξής:

Τον ορισμό του πίνακα: boolean[] prime; μπορούμε να τον βάλουμε μεταξύ των μελών της τάξης AppPanel, στην αρχή της τάξης, εκεί όπου ορίζονται και τα άλλα μέλη της AppPanel, όπως τα appMain, screenPainted, και backgrColor.

Τη δημιουργία του πίνακα: prime = new boolean[100]; μπορούμε να τη βάλουμε στον κατασκευαστή της AppPanel, π.χ. αμέσως μετά την εντολή setBackground (backgrColor);.

Θα πρέπει να φτιάξουμε μια νέα μέθοδο, την BuildPrimesArray, ως εξής:

Τη μέθοδο αυτή πρέπει να την καλούμε όχι στην paint πλέον, αλλά κάπου αλλού, όταν ο χρήστης του προγράμματος δίνει κάποιο σήμα στο πρόγραμμα ώστε να ξεκινήσει ο υπολογισμός των πρώτων αριθμών και το γέμισμα του πίνακα. Ένα βολικό τέτοιο σημείο είναι η μέθοδος keyTyped. Μπορούμε π.χ. να κάνουμε το πρόγραμμά μας να καλεί την BuildPrimesArray όταν πατάμε το πλήκτρο [a], ως εξής:

Τέλος, πρέπει με κάποιον τρόπο να βλέπουμε το αποτέλεσμα της BuildPrimesArray στην οθόνη, το οποίο όπως γνωρίζουμε γίνεται μέσω της paint. Για το σκοπό αυτό θα φτιάξουμε μια άλλη μέθοδο, την PaintPrimes, που θα δείχνει κάθε πρώτο αριθμό με μια κόκκινη κουκκίδα, και κάθε σύνθετο (μη πρώτο) με μια μπλε κουκκίδα.

Άσκηση 3.1: Να κατασκευαστεί η PaintPrimes, όπως μόλις περιγράφηκε. Φυσικά, η μέθοδος PaintPrimes πρέπει να χρησιμοποιεί τον πίνακα prime, που ενημερώνεται όποτε πατάμε το πλήκτρο [a]. Για να εμφανίσουμε μία κόκκινη κουκκίδα στην οθόνη στο σημείο με συντεταγμένες x, y μπορούμε να χρησιμοποιήσουμε τις εντολές: g.setColor(Color.red); και g.fillRect(x, y, 1, 1); όπου η πρώτη θέτει το χρώμα σε κόκκινο, και η δεύτερη ζωγραφίζει ένα ορθογώνιο με πλάτος 1 και ύψος 1 (δηλαδή μία κουκκίδα, ένα pixel).
Υπόδειξη 1: Για να εξετάζουμε αν ο αριθμός i είναι πρώτος, μπορούμε να γράψουμε: if (prime[i]).
Υπόδειξη 2: Όταν πρωτοεκτελείται το πρόγραμμα, και πριν να πατήσουμε το [a], ο πίνακας prime δεν θα έχει ενημερωθεί ακόμα. Άρα με κάποιον τρόπο πρέπει να αποφεύγουμε την εμφάνιση των περιεχομένων του prime πριν καν πατήσουμε το [a].

Προγραμματισμός υπολογιστών

Προαπαιτούμενα και στόχος του μαθήματος

Προαπαιτούμενα