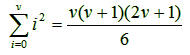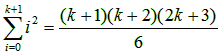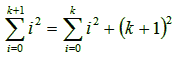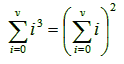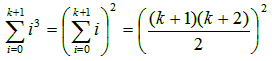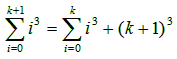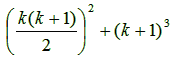|
Εδώ περιλαμβάνονται λύσεις ασκήσεων του μαθήματος
Υ5, αλλά όχι
όλες · μόνο εκείνες που,
κατά την κρίση του συγγραφέα, απαιτούν μια κάποια προσπάθεια.
 Άσκηση 1.3.1: Θέλουμε
να δείξουμε οτι:
Άσκηση 1.3.1: Θέλουμε
να δείξουμε οτι:
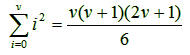 |
|
(1) |
1. Επαγωγική βαση: ν = 0. Τότε η (1) γίνεται 0 = 0
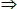 ισχύει
τετριμμένα. ισχύει
τετριμμένα.
2. Επαγωγικό βήμα: έστω οτι η (1) ισχύει για ν =
k
· θέλουμε να δείξουμε οτι ισχύει για ν =
k + 1. Επομένως θέλουμε να δείξουμε
οτι:
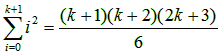 |
|
(2) |
Το αριστερό μέλος της ισότητας (2) γράφεται:
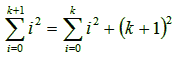
Από την επαγωγική υπόθεση, το παραπάνω ισούται με:
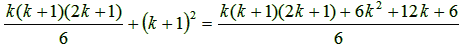
Αναλύοντας περαιτέρω τον αριθμητή του παραπάνω
κλάσματος βρίσκουμε οτι ισούται με το εξής πολυώνυμο:
2
k
3
+ 9
k 2
+ 13
k
+ 6
Κάνοντας τώρα τις πράξεις στον αριθμητή του δεξιού
μέλους της (2), βρίσκουμε ακριβώς το ίδιο πολυώνυμο:
2
k
3
+ 9
k 2
+ 13
k
+ 6
Επομένως η (2) ισχύει.
▓
 Άσκηση 1.3.2: Θέλουμε
να δείξουμε οτι:
Άσκηση 1.3.2: Θέλουμε
να δείξουμε οτι:
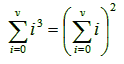 |
|
(1) |
1. Επαγωγική βαση: ν = 0. Τότε η (1) γίνεται 0 = 0
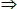 ισχύει
τετριμμένα. ισχύει
τετριμμένα.
2. Επαγωγικό βήμα: έστω οτι η (1) ισχύει για ν =
k
· θέλουμε να δείξουμε οτι ισχύει για ν =
k + 1. Επομένως θέλουμε να δείξουμε
οτι:
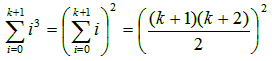 |
|
(2) |
όπου χρησιμοποιήσαμε τον τύπο για το άθροισμα των
k+1 ακεραίων από το
παράδειγμα των σημειώσεων.
Το αριστερό μέλος της ισότητας (2) γράφεται:
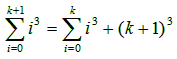
Από την επαγωγική υπόθεση, το δεξί μέλος της
παραπάνω ισότητας ισούται με:
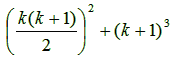
Κάνοντας τις πράξεις, βρίσκουμε οτι το παραπάνω
ισούται με το εξής πολυώνυμο:
(k
4 + 6
k
3
+ 13
k 2
+ 12
k
+ 4) / 4
Κάνοντας τις πράξεις και στο αριστερό μέλος της
(2), βρίσκουμε ακριβώς το ίδιο πολυώνυμο. Επομένως η (2) ισχύει.
▓
 Άσκηση 2.1.1:
Άσκηση 2.1.1:
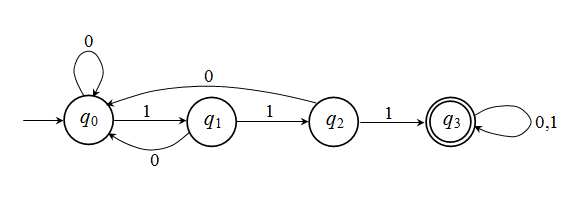
 Άσκηση 2.1.2:
Άσκηση 2.1.2:
 Άσκηση 2.1.5: Η συνάρτηση μετάβασης δ
μπορεί να μετατραπεί σε ολική δ΄ αν ορίσουμε μια κατάσταση
q΄,
που να μην είναι τελική, και στην οποία να καταλήγει η δ παντού όπου
προηγουμένως δεν οριζόταν· ενώ από την
q΄ η δ
καταλήγει και πάλι στην
q΄ με οποιοδήποτε σύμβολο εισόδου.
Έτσι, ο πίνακας της ολικής δ΄ που επεκτείνει τη μερική δ του
“ΠΑ του ανελκυστήρα” θα είναι ο εξής:
Άσκηση 2.1.5: Η συνάρτηση μετάβασης δ
μπορεί να μετατραπεί σε ολική δ΄ αν ορίσουμε μια κατάσταση
q΄,
που να μην είναι τελική, και στην οποία να καταλήγει η δ παντού όπου
προηγουμένως δεν οριζόταν· ενώ από την
q΄ η δ
καταλήγει και πάλι στην
q΄ με οποιοδήποτε σύμβολο εισόδου.
Έτσι, ο πίνακας της ολικής δ΄ που επεκτείνει τη μερική δ του
“ΠΑ του ανελκυστήρα” θα είναι ο εξής:
| δ |
0 |
1 |
2 |
| q0 |
q0 |
q΄ |
q2 |
| q1 |
q0 |
q1 |
q΄ |
| q2 |
q΄ |
q1 |
q2 |
| q΄ |
q΄ |
q΄ |
q΄ |
Δεν είναι δύσκολο να δούμε οτι η το ΠΑ
με τη δ΄ αποδέχεται όλες τις συμβολοσειρές που αποδέχεται και το ΠΑ με
τη δ, ενώ απορρίπτει όλες τις συμβολοσειρές που καταλήγουν στην
q΄, δηλαδή
εκεί όπου η δ δεν οριζόταν.
Ο γράφος του “ΠΑ του ανελκυστήρα” με τη δ΄ είναι τώρα
ο εξής:
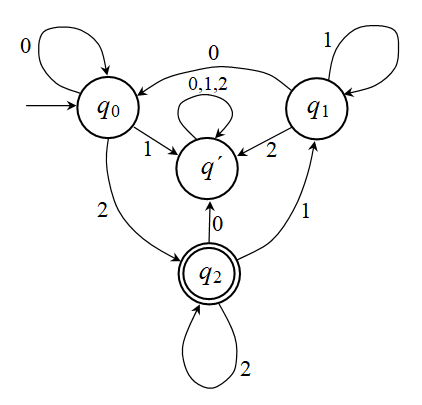
 Άσκηση 2.1.6: Περιγραφή στα ελληνικά:
πρόκειται για όλες τις συμβολοσειρές που ξεκινούν με έναν
προαιρετικό αριθμό από 1 (προαιρετικό = μπορεί και κανένα), και
συνεχίζουν με ένα ή περισσότερα ζεύγη από 01.
Άσκηση 2.1.6: Περιγραφή στα ελληνικά:
πρόκειται για όλες τις συμβολοσειρές που ξεκινούν με έναν
προαιρετικό αριθμό από 1 (προαιρετικό = μπορεί και κανένα), και
συνεχίζουν με ένα ή περισσότερα ζεύγη από 01.
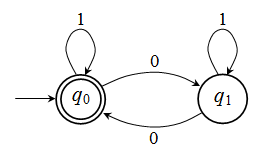
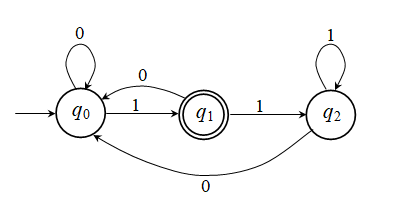
 Άσκηση 2.1.7:
Είναι κανονική γλώσσα, αποτελούμενη από συμβολοσειρές που τελειώνουν
σε 01, ή και απλώς η συμβολοσειρά 1. Ο γράφος ενός ΠΑ που κάνει αποδεκτή τη γλώσσα αυτή είναι ο
εξής:
Άσκηση 2.1.7:
Είναι κανονική γλώσσα, αποτελούμενη από συμβολοσειρές που τελειώνουν
σε 01, ή και απλώς η συμβολοσειρά 1. Ο γράφος ενός ΠΑ που κάνει αποδεκτή τη γλώσσα αυτή είναι ο
εξής:
 Άσκηση 2.2.1: Το ΜΠΑ:
Άσκηση 2.2.1: Το ΜΠΑ:
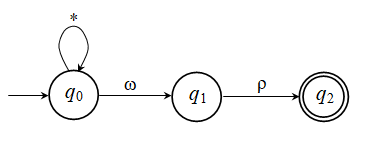
Το αντίστοιχο
ΑΠΑ (όπου * = “οποιοδήποτε γράμμα”, * - ω = “οποιοδήποτε γράμμα εκτός
του ω”, κλπ):
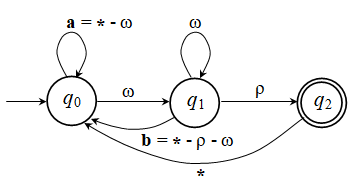
Παρατηρούμε οτι
το ΑΠΑ είναι πιο πολύπλοκο από το ΜΠΑ.
 Άσκηση 2.3.1: Το σύνολο
Q΄ των καταστάσεων του ισοδύναμου ΑΠΑ
είναι το δυναμοσύνολο
P
(Q),
δηλαδή το Q΄ = {
Άσκηση 2.3.1: Το σύνολο
Q΄ των καταστάσεων του ισοδύναμου ΑΠΑ
είναι το δυναμοσύνολο
P
(Q),
δηλαδή το Q΄ = { ,
{q0},
{q1},
{q0,
q1}}.
Επομένως το F΄ είναι το υποσύνολο: {{q1},
{q0,
q1}}. ,
{q0},
{q1},
{q0,
q1}}.
Επομένως το F΄ είναι το υποσύνολο: {{q1},
{q0,
q1}}.
Ακολουθώντας
την κατασκευή του ΑΠΑ σύμφωνα με το θεώρημα 2.3.1, και χρησιμοποιώντας
τα σύμβολα {Qe,
Q0,
Q1,
Q2}
αντί των { ,
{q0},
{q1},
{q0,
q1}}
για το Q΄, παίρνουμε τον εξής γράφο για τη δ΄: ,
{q0},
{q1},
{q0,
q1}}
για το Q΄, παίρνουμε τον εξής γράφο για τη δ΄:
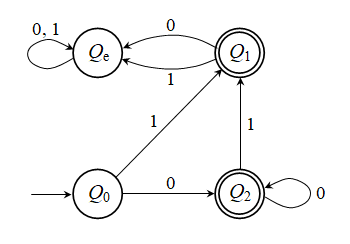
 Άσκηση 2.3.2: Το μόνο που μπορούμε να
κάνουμε για να ελαχιστοποιήσουμε το ΑΠΑ της άσκησης 2.3.1 είναι να
εξαλείψουμε την κατάσταση Qe,
λαμβάνοντας τον εξής γράφο:
Άσκηση 2.3.2: Το μόνο που μπορούμε να
κάνουμε για να ελαχιστοποιήσουμε το ΑΠΑ της άσκησης 2.3.1 είναι να
εξαλείψουμε την κατάσταση Qe,
λαμβάνοντας τον εξής γράφο:
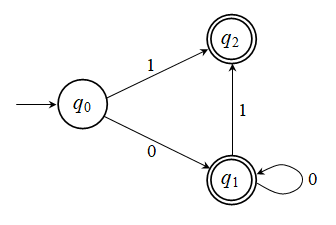
Οι καταστάσεις
μεταξύ των δύο ΑΠΑ είναι προφανώς ισοδύναμες ως εξής: q0
 Q0, q1 Q0, q1
 Q2,
και q2 Q2,
και q2
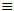 Q1. Q1.
 Άσκηση 2.4.1:
Άσκηση 2.4.1:
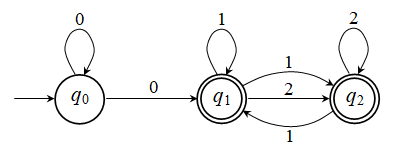
 Άσκηση 2.4.2: Η μόνη αλλαγή σε σχέση
με το ΜΠΑ-ε της Εικ.
2.4.1, είναι οτι η μετάβαση από την q0
στην q1
μπορεί να γίνει με μια μετάβαση-ε αντί μέσω του συμβόλου 0:
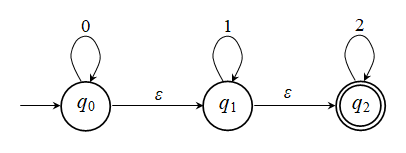
Άσκηση 2.4.2: Η μόνη αλλαγή σε σχέση
με το ΜΠΑ-ε της Εικ.
2.4.1, είναι οτι η μετάβαση από την q0
στην q1
μπορεί να γίνει με μια μετάβαση-ε αντί μέσω του συμβόλου 0:
 Άσκηση 2.5.1: {a,
aba, aa, abaaba, aaba, abaa, aaa, aaaba, abaaa, ...}.
Πρόκειται για τις συμβολοσειρές που έχουν τουλάχιστον ένα
a, και όταν έχουν b
τότε αυτό το b περιστοιχίζεται από ένα ή
περισσότερα a.
Άσκηση 2.5.1: {a,
aba, aa, abaaba, aaba, abaa, aaa, aaaba, abaaa, ...}.
Πρόκειται για τις συμβολοσειρές που έχουν τουλάχιστον ένα
a, και όταν έχουν b
τότε αυτό το b περιστοιχίζεται από ένα ή
περισσότερα a.
 Άσκηση 2.5.2: (1 + ε)(0
+ 01)*.
Άσκηση 2.5.2: (1 + ε)(0
+ 01)*.
 Άσκηση 2.5.3: 0*1*2*.
Άσκηση 2.5.3: 0*1*2*.
 Άσκηση 2.6.1: Δίνεται ο τελικός γράφος
του ΜΠΑ-ε:
Άσκηση 2.6.1: Δίνεται ο τελικός γράφος
του ΜΠΑ-ε:
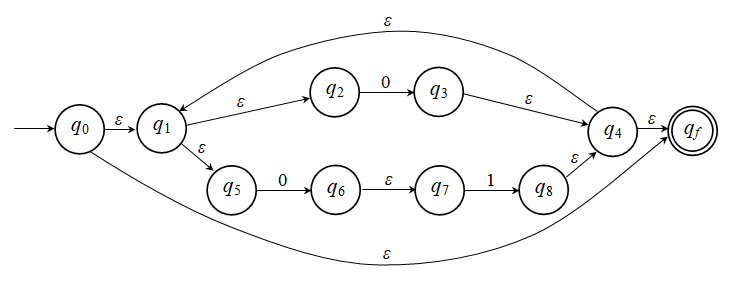
Οι καταστάσεις
έχουν επανονομαστεί (σε σχέση με τα ονόματα που είχαν στα επί μέρους
αυτόματα).
 Άσκηση 2.7.2: Η Μηχανή Μουρ μπορεί να
έχει ως αλφάβητο εξόδου το {0, 1}, και η κατάσταση
q να αντιστοιχεί σε τελική
κατάσταση του ΑΠΑ αν και μόνο αν λ(q)
= 1.
Άσκηση 2.7.2: Η Μηχανή Μουρ μπορεί να
έχει ως αλφάβητο εξόδου το {0, 1}, και η κατάσταση
q να αντιστοιχεί σε τελική
κατάσταση του ΑΠΑ αν και μόνο αν λ(q)
= 1.
 Άσκηση 2.7.3: Έστω η Μηχανή Μουρ Μ1
=
(Q, Σ, Δ, δ, λ,
q0).
Η ζητούμενη Μηχανή Μήλυ είναι η
Μ2
=
(Q, Σ, Δ, δ, λ΄,
q0),
όπου η λ΄ ορίζεται απλούστατα ως εξής: λ΄(q,
a) = λ(δ(q,
a)). Επομένως η
Μ2 σε κάθε μετάβαση από την
κατάσταση q δίνει σαν έξοδο το
σύμβολο εξόδου που δίνει η
Μ1 στην κατάσταση q.
Άσκηση 2.7.3: Έστω η Μηχανή Μουρ Μ1
=
(Q, Σ, Δ, δ, λ,
q0).
Η ζητούμενη Μηχανή Μήλυ είναι η
Μ2
=
(Q, Σ, Δ, δ, λ΄,
q0),
όπου η λ΄ ορίζεται απλούστατα ως εξής: λ΄(q,
a) = λ(δ(q,
a)). Επομένως η
Μ2 σε κάθε μετάβαση από την
κατάσταση q δίνει σαν έξοδο το
σύμβολο εξόδου που δίνει η
Μ1 στην κατάσταση q.
 Άσκηση 3.1.2: το (ανοιχτό + μεγάλο)+
(κουτί + παράθυρο) (έκλεισε + χάλασε) (εντελώς + θορυβωδώς)
Άσκηση 3.1.2: το (ανοιχτό + μεγάλο)+
(κουτί + παράθυρο) (έκλεισε + χάλασε) (εντελώς + θορυβωδώς)
 Άσκηση 3.1.3:
Παράδειγμα διαδοχικών φράσεων:
Άσκηση 3.1.3:
Παράδειγμα διαδοχικών φράσεων:
-
ο καρπός ωρίμασε
-
ο καρπός του δέντρου που επέζησε
ωρίμασε
-
ο καρπός του δέντρου του κήπου που
ποτίστηκε που επέζησε ωρίμασε
-
ο καρπός του δέντρου του κήπου του
σπιτιού που αγοράστηκε που ποτίστηκε που επέζησε ωρίμασε
-
(... κ.ο.κ. ...)
 Άσκηση 3.2.1: Κανόνες:
Άσκηση 3.2.1: Κανόνες:
(Α)
S → αβ | αSβ
(Β)
S → ε | αSβ
 Άσκηση 3.2.2: Κανόνες:
Άσκηση 3.2.2: Κανόνες:
S → αSβ
| β
 Άσκηση 3.2.3: Κανόνες:
Άσκηση 3.2.3: Κανόνες:
S → αSβ
| αS | α
 Άσκηση 3.2.4: Κανόνες:
Άσκηση 3.2.4: Κανόνες:
S → ε | α | β | αSα
| βSβ
 Άσκηση 3.2.5: Κανόνες:
Άσκηση 3.2.5: Κανόνες:
S → ε | αSβ |
βSα
 Άσκηση 3.4.1: Από τον 1ο αλγόριθμο,
βρίσκουμε οτι κανένα τερματικό σύμβολο δεν παράγεται από το Β.
Επομένως διαγράφουμε το Β και τον κανόνα
S → ΑΒ. Στη
συνέχεια, εφαρμόζοντας το 2ο αλγόριθμο στη γραμματική
με Ρ = { S
→ α , Α → α }
βρίσκουμε οτι μόνο το S μπορεί να
εμφανιστεί σε παραγωγές. Άρα η ισοδύναμη γραμματική χωρίς άχρηστα
σύμβολα είναι η: ({S}, {α}, {S
→ α}, S}.
Άσκηση 3.4.1: Από τον 1ο αλγόριθμο,
βρίσκουμε οτι κανένα τερματικό σύμβολο δεν παράγεται από το Β.
Επομένως διαγράφουμε το Β και τον κανόνα
S → ΑΒ. Στη
συνέχεια, εφαρμόζοντας το 2ο αλγόριθμο στη γραμματική
με Ρ = { S
→ α , Α → α }
βρίσκουμε οτι μόνο το S μπορεί να
εμφανιστεί σε παραγωγές. Άρα η ισοδύναμη γραμματική χωρίς άχρηστα
σύμβολα είναι η: ({S}, {α}, {S
→ α}, S}.
 Άσκηση 3.4.2: Εφαρμόζοντας πρώτα το 2ο
αλγόριθμο θα βρίσκαμε οτι όλα τα σύμβολα εμφανίζονται παραγόμενα
εντός συμβολοσειρών. Εφαρμόζοντας μετά τον 1ο αλγόριθμο θα
καταλήγαμε με τους κανόνες
{ S
→ α , Α →
α }, που όμως έχουν ένα άχρηστο σύμβολο, το Α, από το οποίο δεν θα
είχαμε απαλλαγεί.
Άσκηση 3.4.2: Εφαρμόζοντας πρώτα το 2ο
αλγόριθμο θα βρίσκαμε οτι όλα τα σύμβολα εμφανίζονται παραγόμενα
εντός συμβολοσειρών. Εφαρμόζοντας μετά τον 1ο αλγόριθμο θα
καταλήγαμε με τους κανόνες
{ S
→ α , Α →
α }, που όμως έχουν ένα άχρηστο σύμβολο, το Α, από το οποίο δεν θα
είχαμε απαλλαγεί.
 Άσκηση 4.2.1: Για το θ. 4.2.1, όταν
φτάσουμε σε τελική κατάσταση αρκεί να προσθέσουμε μεταβάσεις στη δ
για να αδειάσει η στοίβα. Για το θ. 4.2.2, όταν αδειάσει η στοίβα
αρκεί να μεταφερθούμε σε μια νέα τελική κατάσταση με σύμβολο εισόδου
το ε (δηλαδή χωρίς κίνηση της κεφαλής επί της εισόδου) και με
τη στοίβα να παραμένει κενή (→ ε).
Οι λεπτομέρειες πάντως, για να καταλήξουμε σε τυπική απόδειξη, είναι
αρκετές.
Άσκηση 4.2.1: Για το θ. 4.2.1, όταν
φτάσουμε σε τελική κατάσταση αρκεί να προσθέσουμε μεταβάσεις στη δ
για να αδειάσει η στοίβα. Για το θ. 4.2.2, όταν αδειάσει η στοίβα
αρκεί να μεταφερθούμε σε μια νέα τελική κατάσταση με σύμβολο εισόδου
το ε (δηλαδή χωρίς κίνηση της κεφαλής επί της εισόδου) και με
τη στοίβα να παραμένει κενή (→ ε).
Οι λεπτομέρειες πάντως, για να καταλήξουμε σε τυπική απόδειξη, είναι
αρκετές.
 Άσκηση 4.4.1: Ένα ΑΣ Μ =
(Q,
Σ, Γ, δ, q0,
Ζ0,
F) είναι
αιτιοκρατικό αν:
Άσκηση 4.4.1: Ένα ΑΣ Μ =
(Q,
Σ, Γ, δ, q0,
Ζ0,
F) είναι
αιτιοκρατικό αν:
-
Για κάθε q
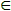 Q και Ζ
Q και Ζ
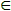 Γ,
όταν το δ (q, ε, Ζ) δεν είναι κενό,
τότε το δ (q, α, Ζ) είναι κενό Γ,
όταν το δ (q, ε, Ζ) δεν είναι κενό,
τότε το δ (q, α, Ζ) είναι κενό
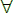 α α
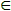 Σ. Σ.
-
Για κανένα q
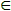 Q, Ζ
Q, Ζ
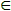 Γ,
και α Γ,
και α
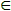 Σ Σ
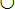 {ε}
δεν ισχύει οτι το δ (q, α, Ζ) περιλαμβάνει
περισσότερα από ένα στοιχεία (μεταβάσεις). {ε}
δεν ισχύει οτι το δ (q, α, Ζ) περιλαμβάνει
περισσότερα από ένα στοιχεία (μεταβάσεις).
Η συνθήκη 1 αποκλείει την περίπτωση
επιλογής μεταξύ μιας κίνησης ανεξάρτητης από το σύμβολο εισόδου (δηλαδή
κενή κίνηση) και μιας κίνησης που βασίζεται σε σύμβολο εισόδου. Η
συνθήκη 2 αποκλείει την επιλογή για οποιοδήποτε (q,
α, Ζ) ή (q, ε, Ζ).
 Άσκηση 4.4.2: Το παρακάτω διάγραμμα
δίνει την απεικόνιση δ για το ΑΣ Μ = ({q1,
q2},
{0, 1, 2}, {●,
●,
●},
δ,
q1, ●,
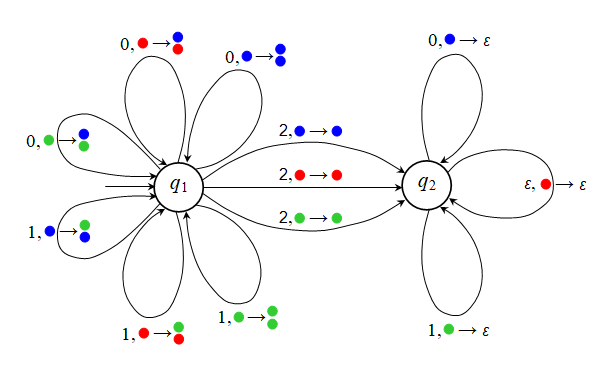
Άσκηση 4.4.2: Το παρακάτω διάγραμμα
δίνει την απεικόνιση δ για το ΑΣ Μ = ({q1,
q2},
{0, 1, 2}, {●,
●,
●},
δ,
q1, ●,
 })
που αποδέχεται τη γλώσσα {
w2wR |
w })
που αποδέχεται τη γλώσσα {
w2wR |
w 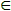 (0 + 1)*}:
(0 + 1)*}:
|