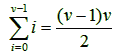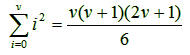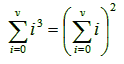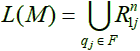 |
Αυτόματα – Τυπικές Γλώσσες – ΥπολογισιμότηταΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ Υ5 ΤΟΥ Δ.Ε.Π. |
|
Προαπαιτούμενα και περιεχόμενα του μαθήματος
Προαπαιτούμενα
Το μάθημα αυτό προϋποθέτει γνώση των θεμελιωδών εννοιών υπολογιστών (μάθημα Υ1), αλλά και μια κάποια μαθηματική παιδεία, καθώς βρίσκεται στην τομή των περιοχών των μαθηματικών και των υπολογιστών. Συγκεκριμένα, απαιτείται γνώση, προηγούμενη εκπαίδευση, και ιδίως ευχέρεια σε μαθηματικές αποδείξεις. Ειδικά η αποδεικτική μέθοδος της μαθηματικής επαγωγής ανασκοπείται στην εισαγωγική ενότητα (επειδή γίνεται χρήση-της σε πάμπολλα θεωρήματα), αλλά ο αναγνώστης δεν πρέπει να αναμένει να μάθει να αποδεικνύει μέσω επαγωγής στο παρόν μάθημα· πρέπει ήδη να κατέχει αυτήν τη δεξιότητα που αποκτάται στο μάθημα Μ1. Βέβαια, η μαθηματική παιδεία δεν αποκτάται μόνο μέσω του μαθήματος Μ1, αλλά με τη γνώση και εκπαίδευση σε μια πλειάδα μαθημάτων μαθηματικού υποβάθρου· π.χ.: Λογική (Μ2), Θεωρία Συνόλων (Μ7), Θεωρία Αριθμών (Μ8), κ.ά.
Περιεχόμενα και στόχος
Το παρόν μάθημα αποτελεί τον “πυρήνα” της περιοχής γνώσης που λέγεται “επιστήμη υπολογιστών”· ήτοι, δεν νοείται να ισχυρίζεται κανείς οτι έχει σπουδάσει επιστήμη υπολογιστών χωρίς να έχει μελετήσει και αποκτήσει γνώση σε βάθος όλων των εννοιών που περιέχονται στο παρόν μάθημα. Ασχολείται με την έννοια της υπολογισιμότητας (αγγλ.: computability), και με τα διάφορα τυπικά συστήματα (αγγλ.: formal systems) μέσω των οποίων μπορούμε να ορίσουμε υπολογιστικές μηχανές. Δύο από αυτά τα τυπικά συστήματα είναι: 1. τα πεπερασμένα αυτόματα (αγγλ.: finite automata), και 2. οι τυπικές γλώσσες (αγγλ.: formal languages). Εξετάζει την ισοδυναμία μεταξύ κατηγοριών αυτομάτων και γλωσσών, και κατασκευάζει έτσι, βήμα-βήμα, το “απόσταγμα” της όλης θεωρίας της υπολογισιμότητας, που είναι η ιεραρχία του Τσόμσκι (αγγλ.: Chomsky hierarchy).
Στόχος του μαθήματος είναι η κατανόηση της έννοιας της υπολογισιμότητας· του πότε ένα πρόβλημα χαρακτηρίζεται αποφασίσιμο (αγγλ.: decidable) και πότε αναποφασίσιμο (αγγλ.: undecidable)· η κατανόηση των τεσσάρων κλάσεων τυπικών συστημάτων που αποτελούν την ιεραρχία του Τσόμσκι· και η κατανόηση σε βάθος του “αποστάγματος” της έννοιας “υπολογιστής”.
Θα μάθουμε για τα χαρακτηριστικά που πρέπει να έχει μια συσκευή έτσι ώστε να μπορούμε να πούμε οτι “υπολογίζει” κάτι. Θα γνωρίσουμε τέσσερις τέτοιες κατηγορίες συσκευών, η κάθε μια “υπολογιστικά πιο ισχυρή” (υπολογίζοντας πιο πολλές συναρτήσεις) από την προηγούμενη κατηγορία, και χωρίς κάποιον άλλο τύπο συσκευής να μπορεί να “χωρέσει ανάμεσα” σ’ αυτές τις τέσσερις. Η τέταρτη των κατηγοριών αυτών συσκευών, που είναι η Μηχανή Τούρινγκ (αγγλ.: Turing Machine), θα αποδειχθεί ο ισχυρότερος υπολογιστής που έχουμε φτιάξει ποτέ. Κάθε επιπλέον δυνατότητα που θα προσθέτουμε στη βασική Μηχανή Τούρινγκ θα αδυνατεί να προσθέσει ισχύ, με την έννοια οτι δεν θα υπάρχει καμιά συνάρτηση που να μπορεί να υπολογιστεί από την επαυξημένη συσκευή και που να μη μπορεί να υπολογιστεί κι από τη βασική Μηχανή Τούρινγκ. Έτσι θα συμπεράνουμε τη λεγόμενη Θέση των Τσερτς–Τούρινγκ, που λέει οτι η Μηχανή Τούρινγκ (ή όποια άλλη ισοδύναμη συσκευή) είναι ο ισχυρότερος υπολογιστής που μπορούμε ποτέ να φανταστούμε. Και, επειδή οι νευρώνες του εγκεφάλου μπορούν μάλλον εύκολα να εξισωθούν με μοντέλα υπολογιστικών συσκευών, η Θέση Τσερτς–Τούρινγκ έχει προεκτάσεις στην ανθρώπινη νόηση, προτείνοντας οτι οι σημερινοί υπολογιστές μπορεί να είναι ισοδύναμοι σε υπολογιστική ισχύ με τον ανθρώπινο εγκέφαλο. Αυτά και αρκετά άλλα ενδιαφέροντα θέματα περιλαμβάνονται στην ύλη του παρόντος μαθήματος.
Σαν βάση των σημειώσεων του παρόντος μαθήματος χρησιμοποιήθηκαν τα βιβλία που αναφέρονται στη βιβλιογραφία.
1. Εισαγωγικές έννοιες
Στην ενότητα αυτή θα κάνουμε μια σύντομη ανασκόπηση των θεμελιωδών εννοιών στις οποίες στηρίζεται και χρησιμοποιεί η θεωρία της υπολογισιμότητας.
1.1 Σύμβολα, αλφάβητα, συμβολοσειρές, και γλώσσες
Όπως η γεωμετρία ξεκινάει με κάποιες έννοιες των οποίων δέχεται την ύπαρξη χωρίς να τις ορίζει (π.χ.: σημείο, ευθεία), έτσι και η παρούσα θεωρία στηρίζεται σε έννοιες χωρίς ορισμό, μία των οποίων είναι η έννοια σύμβολο.* Για την παράσταση συμβόλων θα χρησιμοποιούμε γράμματα, αριθμούς, κλπ., παρμένα από ένα αλφάβητο:
Ορισμός: ένα αλφάβητο είναι ένα πεπερασμένο σύνολο συμβόλων.
Παραδείγματα αλφαβήτων είναι τα: {a, b, c}, {0, 1}, {z, $, 8, -}, κλπ. Συνήθως, για να μη μπερδευόμαστε, θα χρησιμοποιούμε λατινικά γράμματα ή ψηφία για τα σύμβολα ενός αλφαβήτου. Π.χ., από τα προηγούμενα παραδείγματα, τα {a, b, c} και {0, 1} είναι παραδείγματα αλφαβήτων που θα συναντάμε συχνά, καθώς άλλα σύμβολα (π.χ., τα +, *, κ.ά.) θα χρησιμοποιούνται για να δηλώνουν πράξεις μεταξύ αντικειμένων του μαθήματος. Θα χρησιμοποιούμε κεφαλαία ελληνικά γράμματα, όπως το Σ, για να συμβολίσουμε ολόκληρο το αλφάβητο· π.χ., Σ = {a, b}.
Ορισμός: μια συμβολοσειρά (αγγλ.: string) είναι μια ακολουθία συμβόλων που ανήκουν σε ένα αλφάβητο.
Παραδείγματα συμβολοσειρών είναι τα: babba, abba, aaaabbbb, κατασκευασμένα από το αλφάβητο {a, b}, αλλά και από το {a, b, c}, κλπ. Επίσης τα 1000, 1010101010, 000001, κατασκευασμένα από αλφάβητο που περιέχει τουλάχιστον τα σύμβολα 0 και 1· κ.ο.κ.
Δεχόμαστε την ύπαρξη της κενής συμβολοσειράς, που θα τη συμβολίζουμε με το ελληνικό πεζό γράμμα ε (σε πλάγια γραφή).
Θα χρησιμοποιούμε γράμματα σε πλάγια γραφή από το τέλος του λατινικού αλφαβήτου (w, x, y, z) για να δηλώνουμε συμβολοσειρές στη γενικότητά τους. Εξαίρεση θα αποτελεί, όπως είπαμε, η κενή συμβολοσειρά ε.
Ορισμός: το μήκος μιας συμβολοσειράς είναι ο αριθμός των συμβόλων που αποτελούν τη συμβολοσειρά. Θα χρησιμοποιούμε το συμβολισμό |w| για το μήκος της συμβολοσειράς w.
Π.χ., το |abba| είναι ίσο με 4, ενώ |ε| = 0.
Ορισμός: ένα πρόθεμα μιας συμβολοσειράς w είναι ένα αρχικό τμήμα της w· αντίστοιχα, μια κατάληξη της w είναι ένα τελικό τμήμα της w.
Π.χ., το aaa είναι πρόθεμα της aaaaab, ενώ το ab είναι κατάληξη της ίδιας συμβολοσειράς. Προφανώς το ε είναι τόσο πρόθεμα όσο και κατάληξη κάθε συμβολοσειράς. Επίσης προφανώς, κάθε συμβολοσειρά είναι πρόθεμα και κατάληξη του εαυτού-της.
Ορισμός: ένα γνήσιο πρόθεμα, και παρομοίως, μια γνήσια κατάληξη μιας συμβολοσειράς είναι οποιοδήποτε πρόθεμα ή κατάληξή της εκτός του εαυτού-της.
Ορισμός: το αποτέλεσμα της πράξης της συνένωσης (αγγλ.: concatenation) δύο συμβολοσειρών x και y είναι η συμβολοσειρά που προκύπτει από την απλή παράθεσή τους: xy.
Π.χ., η συνένωση των ab και ba είναι η abba. Η συνένωση των 0101 και ε είναι η 0101, που είναι επίσης η συνένωση των ε και 0101.
Η πράξη της συνένωσης έχει ασφαλώς την προσεταιριστική ιδιότητα, καθώς (xy)z = x(yz). Έτσι, θα γράφουμε απλά xyz εννοώντας τη συνένωση των x, y, και z, αφού η προτεραιότητα με την οποία εκτελούνται οι δύο συνενώσεις δεν παίζει ρόλο.
Ορισμός: μια τυπική γλώσσα (που θα την ονομάζουμε και απλώς γλώσσα) είναι ένα σύνολο συμβολοσειρών από το ίδιο αλφάβητο.
Παραδείγματα: το κενό σύνολο Ø, όπως και το σύνολο {ε}, είναι γλώσσες· η πρώτη με πληθάριθμο* 0, ενώ η δεύτερη με πληθάριθμο 1. Ας σημειωθεί οτι μια γλώσσα δεν απαιτείται να είναι πεπερασμένο σύνολο· μπορεί να είναι και άπειρο. Για το ακόλουθο παράδειγμα άπειρης γλώσσας θα χρειαστούμε έναν ορισμό:
Ορισμός: Μια συμβολοσειρά ονομάζεται παλίνδρομο αν (και μόνο αν)* διαβάζεται το ίδιο τόσο από αριστερά προς τα δεξιά όσο και από δεξιά προς τα αριστερά.
Το σύνολο όλων των παλινδρόμων από ένα αλφάβητο είναι μια άπειρη γλώσσα. Για παράδειγμα το σύνολο των παλινδρόμων του αλφαβήτου Σ = {a, b} είναι η γλώσσα: {ε, a, b, aa, bb, aaa, bbb, aba, bab, ...}. Θα χρησιμοποιούμε κεφαλαία λατινικά γράμματα για να συμβολίσουμε γλώσσες, π.χ.: L, G, κλπ.
Μια άλλη γλώσσα είναι το σύνολο όλων των συμβολοσειρών ενός αλφαβήτου Σ. Για τη γλώσσα αυτή θα χρησιμοποιούμε τον συμβολισμό Σ*. (Προσοχή: το Σ είναι αλφάβητο, ενώ το Σ* είναι γλώσσα.) Γενικά, το σύμβολο * θα το χρησιμοποιούμε για μια πράξη επί γλωσσών, που ονομάζεται “κλειστότητα Κλέινι” * (ή κλείσιμο Κλέινι, ή αστέρι Κλέινι· αγγλ.: Kleene closure):
Ορισμός: η κλειστότητα Κλέινι μιας γλώσσας L, που συμβολίζεται με το L*, είναι η γλώσσα που προκύπτει από τη συνένωση οποιουδήποτε αριθμού συμβολοσειρών της L.
Π.χ., αν L = {aa, ba}, τότε L* = {ε, aa, ba, aaaa, aaba, baaa, baba, ...}. Παρατηρούμε οτι η κλειστότητα Κλέινι είναι πάντοτε μια άπειρη γλώσσα.
Η κλειστότητα Κλέινι μπορεί να οριστεί παρόμοια και επί ενός αλφαβήτου Σ: πρόκειται για τη γλώσσα που προκύπτει από συνένωση οποιουδήποτε αριθμού συμβόλων του Σ.
Η πράξη αυτή ονομάζεται “κλειστότητα” (ή “κλείσιμο”) γιατί η επανάληψή της δεν δίνει νέο αποτέλεσμα: (L*)* = L*. Με άλλα λόγια, το σύνολο που προκύπτει έχει “κλείσει” (από άποψη νέων στοιχείων) με τη μία και μοναδική εφαρμογή της πράξης.
Άσκηση 1.1.1: Να αναγραφούν 8 στοιχεία της κλειστότητας L*, όπου L είναι η γλώσσα {ε, a, b, ba}. Μπορεί το ε να είναι ένα από αυτά τα στοιχεία; Μπορεί να είναι το εε;
Η έννοια της κλειστότητας συνόλων είναι πιο γενική, και θα μας απασχολήσει αργότερα, οπότε ας την ορίσουμε:
Ορισμός: Ένα σύνολο λέμε οτι είναι κλειστό ως προς μια δοσμένη πράξη αν η εφαρμογή αυτής της πράξης επί μελών του συνόλου έχει σαν αποτέλεσμα μόνο μέλη του συνόλου.
Για παράδειγμα, οι ακέραιοι είναι σύνολο κλειστό ως προς την πρόσθεση και την αφαίρεση, εφόσον η πρόσθεση και η αφαίρεση ακεραίων δίνει πάλι ακέραιο. Όμως οι φυσικοί αριθμοί είναι μεν κλειστοί ως προς την πρόσθεση, αλλά όχι ως προς την αφαίρεση, αφού αφαιρώντας φυσικό αριθμό μεγαλύτερο από μικρότερο δεν παίρνουμε φυσικό αριθμό.
1.2 Γράφοι και δέντρα
Για την εποπτική παράσταση* των πεπερασμένων αυτομάτων, τα οποία θα γνωρίσουμε στην επόμενη ενότητα, θα χρησιμοποιήσουμε τη δομή του γράφου.
Ορισμός: ένας γράφος G (αγγλ.: graph) είναι ένα διατεταγμένο ζεύγος πεπερασμένων συνόλων (V, E), όπου το V λέγεται το σύνολο των κορυφών (αγγλ.: vertices, ενικός vertex) του γράφου, ενώ το E, που λέγεται το σύνολο των ακμών (αγγλ.: edges) του γράφου, είναι ένα σύνολο (όχι απαραίτητα διατεταγμένων) ζευγών κορυφών από το V (ή αλλιώς: το Ε είναι μια διμελής σχέση του V).
Παράδειγμα:

Εικ. 1.1: Γράφος
Ο παραπάνω γράφος G = (V, E) έχει V = {1, 2, ..., 9} και Ε = {(i, j) | i + j = πρώτος αριθμός}.
Ορισμός: ο κατευθυνόμενος γράφος (αγγλ.: directed graph) είναι ένας γράφος του οποίου το σύνολο των ακμών Ε είναι σύνολο διατεταγμένων ζευγών κορυφών από το V.
Συνεπώς, σε έναν κατευθυνόμενο γράφο έχει σημασία το “από” και το “προς” μιας ακμής (από ποια κορυφή ξεκινάει και προς ποια κορυφή καταλήγει). Ακολουθεί ένα παράδειγμα κατευθυνόμενου γράφου.

Εικ. 1.2: Κατευθυνόμενος γράφος
Ο παραπάνω γράφος G = (V, E) έχει V = {2, 3, ..., 9} και Ε = {(i, j) | i < j και i διαιρεί το j}.
Ορισμός: μια
διαδρομή (αγγλ.:
path) σε
έναν γράφο G = (V, E) είναι μια ακολουθία
κορυφών v1,
v2, ..., vk
από το V, με
k > 0, έτσι ώστε να υπάρχει ακμή (vi,
vi+1)
![]() i, 1
i, 1
![]() i < k. Το
μήκος μιας τέτοιας διαδρομής είναι k
– 1.
i < k. Το
μήκος μιας τέτοιας διαδρομής είναι k
– 1.
Όπως βλέπουμε από το προηγούμενο παράδειγμα, ένας γράφος δεν είναι απαραίτητο να είναι “ένα κομμάτι”. Όταν ο γράφος είναι “ένα κομμάτι”, ονομάζεται “συνεκτικός” (αγγλ.: connected). Όμως για όλες τις εποπτικές παραστάσεις πεπερασμένων αυτομάτων θα χρησιμοποιήσουμε κατευθυνόμενους γράφους, κανένας από τους οποίους δεν θα είναι “δύο κομμάτια” (ή περισσότερα). Γιαυτό δεν χρειάζεται να ορίσουμε τη συνεκτικότητα γράφων με τυπικό τρόπο.
Άσκηση 1.2.1: Να σχεδιαστεί ο γράφος G = (V, E) όπου V = {2, 3, ..., 9} και Ε = {(i, j) | i & j είναι πρώτοι προς αλλήλους}. (Δύο αριθμοί ονομάζονται “πρώτοι προς αλλήλους” όταν δεν έχουν κοινό διαιρέτη άλλον από τη μονάδα.) Είναι ο G κατευθυνόμενος ή μη; Υπάρχει διαδρομή από το 2 στο 8 στον G;
Ορισμός: σε μια ακμή (u, v) κατευθυνόμενου γράφου G, η κορυφή u λέγεται προκάτοχος της v, ενώ η v λέγεται διάδοχος της u.
Ορισμός: ένα δέντρο είναι ένας κατευθυνόμενος γράφος στον οποίο ισχύουν τα εξής:
-
Υπάρχει μία κορυφή, που ονομάζεται ρίζα, που δεν έχει προκάτοχο, και από την οποία υπάρχει διαδρομή προς κάθε κορυφή.
-
Κάθε κορυφή εκτός της ρίζας έχει ακριβώς έναν προκάτοχο.
-
Οι διάδοχοι κάθε κορυφής είναι διατεταγμένοι.
Η διάταξη των διαδόχων μιας κορυφής σε ένα δέντρο (συνθήκη 3) μας επιτρέπει να τους σχεδιάζουμε από αριστερά προς τα δεξιά όταν δίνουμε τη γραφική απεικόνιση του δέντρου. Στις απεικονίσεις, τα δέντρα θα τα σχεδιάζουμε “ανάποδα”, με τη ρίζα επάνω και τους διαδόχους κάθε κορυφής από κάτω, διατεταγμένους.* Στο διάγραμμα που ακολουθεί δίνεται παράδειγμα ενός δέντρου, όπου κάθε κορυφή είναι το γινόμενο των διαδόχων-της.
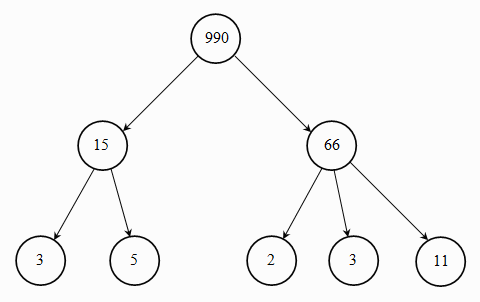
Εικ. 1.3: Δέντρο
Το παραπάνω δέντρο θα μπορούσε να οριστεί ως μια ανάλυση του αριθμού 990 σε γινόμενο πρώτων παραγόντων. Δέντρα θα χρησιμοποιήσουμε κυρίως για την παράσταση γραμματικών (“χωρίς συμφραζόμενα” και “με συμφραζόμενα”), σε επόμενες ενότητες. Προκειμένου για δέντρα, χρησιμοποιούμε μια κάπως πιο εξειδικευμένη ορολογία:
Ορισμός: σε ένα δέντρο, ο προκάτοχος λέγεται γονέας, ενώ οι διάδοχοι λέγονται τέκνα.
Π.χ., στο δέντρο του προηγούμενου παραδείγματος, ο γονέας της κορυφής που σημειώνεται με το “5” είναι η κορυφή “15”, ενώ τα τέκνα του “990” είναι τα “15” και “66”.
1.3 Αποδείξεις μέσω επαγωγής
Εδώ κάνουμε μια σύντομη ανασκόπηση της αποδεικτικής μεθόδου της μαθηματικής επαγωγής. Έστω οτι έχουμε μια πρόταση Π(ν), που εξαρτάται από ένα φυσικό αριθμό ν, και παίρνει τιμές “αλήθεια” ή “ψέμα” (πρόκειται δηλαδή για ένα κατηγόρημα). Η αρχή της μαθηματικής επαγωγής λέει οτι για να αποδείξουμε οτι η Π(ν) είναι αληθής, αρκεί να αποδείξουμε οτι:
-
Π(0), και
-
Π(ν – 1) → Π(ν)
 ν
ν
 1.
1.
Τη συνθήκη (1), παραπάνω, τη λέμε επαγωγική βάση, ενώ τη συνθήκη (2) τη λέμε επαγωγικό βήμα. Τη σχέση Π(ν – 1) στην (2) τη λέμε επαγωγική υπόθεση (αγγλ.: inductive basis, step, & hypothesis).
Παράδειγμα: έστω οτι η πρόταση Π(ν) που θέλουμε να αποδείξουμε είναι η εξής ισότητα:
Αποδεικνύουμε την Π(ν) με επαγωγή. Η επαγωγική βάση, Π(0), ισχύει κατά τετριμμένο τρόπο: 0 = 0(0+1)/2, ήτοι 0 = 0. Για το επαγωγικό βήμα τώρα, έχουμε από την υπόθεση Π(ν – 1) πως ισχύει οτι:
![]() ν
ν
![]() 1, και θέλουμε να
συνάγουμε την Π(ν). Προσθέτοντας το ν και στα δύο μέλη της Π(ν
– 1), παίρνουμε:
1, και θέλουμε να
συνάγουμε την Π(ν). Προσθέτοντας το ν και στα δύο μέλη της Π(ν
– 1), παίρνουμε:
Παρατηρούμε οτι το αριστερό και το δεξί μέλος της παραπάνω πολλαπλής ισότητας είναι ακριβώς η Π(ν). Άρα η Π(ν) ισχύει. ▓
(Στην παραπάνω απόδειξη βλέπουμε και τη χρήση του συμβόλου ▓ που θα κάνουμε για να συμβολίζουμε το «όπερ έδει δείξαι» στο τέλος κάθε απόδειξης.)
![]() Άσκηση 1.3.1: Να αποδειχτεί με χρήση επαγωγής ως
προς ν η ισότητα:
Άσκηση 1.3.1: Να αποδειχτεί με χρήση επαγωγής ως
προς ν η ισότητα:
![]() Άσκηση 1.3.2: Να αποδειχτεί με χρήση επαγωγής ως
προς ν η ισότητα:
Άσκηση 1.3.2: Να αποδειχτεί με χρήση επαγωγής ως
προς ν η ισότητα:
Ας δούμε και μια εφαρμογή της επαγωγής όχι σε ισότητες, αλλά στο μήκος συμβολοσειρών, που θα είναι το είδος της επαγωγής που θα συναντάμε πιο συχνά στο παρόν μάθημα.
Όπως αναφέρθηκε και νωρίτερα, ο ορισμός ενός παλινδρόμου λέει οτι είναι μια συμβολοσειρά που διαβάζεται το ίδιο τόσο από αριστερά προς τα δεξιά, όσο και από δεξιά προς τα αριστερά. Π.χ., οι ακόλουθες συμβολοσειρές (πασίγνωστες στους ομιλητές των αντίστοιχων γλωσσών) είναι παλίνδρομα:
νιψονανομηματαμημονανοψιν
madaminedenimadam
Θέλουμε τώρα να αποδείξουμε το παρακάτω:
Θεώρημα 1.1: μια συμβολοσειρά x είναι παλίνδρομο τότε και μόνο τότε όταν είναι μέλος του μικρότερου συνόλου P το οποίο:
-
περιλαμβάνει το ε,
-
περιλαμβάνει κάθε σύμβολο a του αλφαβήτου,
-
περιλαμβάνει όλες τις συμβολοσειρές της μορφής aya όπου το a είναι οποιοδήποτε σύμβολο και y
 P.
P.
|
Απόδειξη. Η κατεύθυνση “τότε” του θεωρήματος
είναι μάλλον προφανής, γιατί αν το x
Ας υποθέσουμε οτι η συμβολοσειρά
x είναι παλίνδρομο, δηλαδή διαβάζεται το ίδιο και προς τις δύο
διευθύνσεις. Θα αποδείξουμε το θεώρημα μέσω
επαγωγής επί του μήκους του x. Αν |x|
|
2. Πεπερασμένα Αυτόματα
2.1 Αιτιοκρατικά Πεπερασμένα Αυτόματα
Ένα πεπερασμένο αυτόματο (ΠΑ, αγγλ.: finite automaton) είναι ένα μαθηματικό μοντέλο ενός συστήματος (μπορεί να είναι ένα φυσικό σύστημα — θα δούμε παραδείγματα αμέσως) που ανά πάσα στιγμή μπορεί να βρίσκεται σε μια κατάσταση ή καταστάσεις (αγγλ.: states), έχοντας επεξεργαστεί κάποια δεδομένα εισόδου (αγγλ.: input data). Προαιρετικά, το ΠΑ μπορεί να έχει αποδεχτεί (αγγλ.: accepted) τα δεδομένα εισόδου ευρισκόμενο σε μια τελική κατάσταση (αγγλ.: final state)· αλλιώς, αν τα δεδομένα εισόδου τελείωσαν και το ΠΑ δεν βρίσκεται σε τελική κατάσταση, τότε απορρίπτει (αγγλ.: rejects) τα δεδομένα εισόδου. Προαιρετικά επίσης, μπορεί κατά τη λειτουργία-του να έχει δημιουργήσει ορισμένα δεδομένα εξόδου (αγγλ.: output data).
Απλό παράδειγμα ενός ΠΑ είναι ένας ανελκυστήρας παλαιού τύπου (ηλεκτρικός, όχι ηλεκτρονικός). Η κατάσταση στην οποία βρίσκεται ο ηλεκτρικός ανελκυστήρας είναι ο όροφος στον οποίο σταθμεύει ανά πάσα στιγμή, ενώ χάριν απλότητας αγνοούμε το χρόνο που μεσολαβεί καθώς ο ανελκυστήρας κινείται από όροφο σε όροφο. Τα δεδομένα εισόδου που έχει επεξεργαστεί ο ανελκυστήρας είναι τα κουμπιά κλήσης που πατήθηκαν είτε από χρήστες που εξυπηρετήθηκαν από διάφορους ορόφους, είτε μέσα από τον ανελκυστήρα. Ο ηλεκτρικός ανελκυστήρας δεν έχει μνήμη, συνεπώς το κάθε κουμπί κλήσης που πατιέται σε έναν όροφο μπαίνει σαν “επόμενο δεδομένο εισόδου” αν ο ανελκυστήρας δεν κινείται. (Αν κινείται, τα πατήματα κουμπιών αγνοούνται σε τέτοιους ανελκυστήρες.) Γίνεται άμεση επεξεργασία αυτού του δεδομένου εισόδου, δηλαδή ο ανελκυστήρας αλλάζει κατάσταση, μεταφερόμενος στον όροφο που έγινε η κλήση. Επίσης, ο ανελκυστήρας (γενικά) είναι κάπως ειδικού τύπου αυτόματο, γιατί δεν έχει τελική κατάσταση (δεν σταματά να λειτουργεί ποτέ· δεν έρχεται ποτέ σε κατάσταση “τέλος, δεν εξυπηρετώ άλλα δεδομένα”).
Ο ακόλουθος γράφος δείχνει σχηματικά ένα ΠΑ που αποτελεί μοντέλο ανελκυστήρα για τρεις ορόφους:

Εικ. 2.1.1: ΠΑ ανελκυστήρα τριών ορόφων
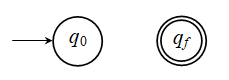
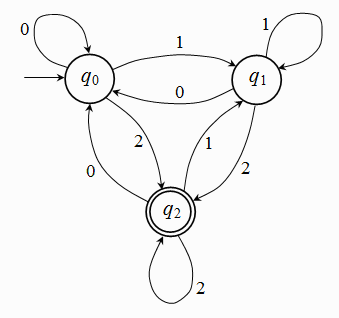
Στον παραπάνω γράφο, το ΠΑ που απεικονίζεται “μοντελοποιεί” έναν ανελκυστήρα τριών ορόφων, όπου η κατάσταση q0 σημαίνει οτι ο ανελκυστήρας είναι σταθμευμένος στο ισόγειο, η q1 στον πρώτο όροφο, και η q2 στο δεύτερο όροφο. Τα βέλη που φεύγουν από κάθε κατάσταση δείχνουν σε ποια κατάσταση θα βρεθεί το αυτόματο με το πάτημα του κουμπιού του αντίστοιχου ορόφου. Π.χ., όταν ο ανελκυστήρας είναι στο ισόγειο (q0), το πάτημα του κουμπιού του ισογείου (0) δεν έχει κανένα αποτέλεσμα, και ο ανελκυστήρας παραμένει στην κατάσταση q0. Αντίθετα, από την q0, με το πάτημα του κουμπιού για τον πρώτο όροφο, το ΠΑ μεταφέρεται στην κατάσταση q1 (“στάθμευση στον πρώτο όροφο”), ενώ με το πάτημα του κουμπιού για το δεύτερο όροφο μεταφέρεται αντίστοιχα στην κατάσταση q2 (“στάθμευση στο δεύτερο όροφο”). Τα κουμπιά 0, 1, και 2 είναι τα δεδομένα εισόδου. Η κάθε κατάσταση qi πρέπει να ανταποκρίνεται σε κάθε δεδομένο εισόδου i, οπου i = 0, 1, 2, προκειμένου ο ανελκυστήρας να λειτουργεί σωστά. Επίσης βλέπουμε μια σύμβαση που θα κάνουμε στα διαγράμματα όλων των αυτομάτων: η αρχική κατάσταση (q0) θα διακρίνεται από τις άλλες με το βέλος που καταλήγει σ’ αυτήν “από το πουθενά” (οριζόντιο στο σχήμα).
Ο ηλεκτρονικός ανελκυστήρας διαφέρει κατά ουσιαστικό τρόπο από τον ηλεκτρικό, γιατί περνάει από κατάσταση σε κατάσταση κατά διαφορετικό τρόπο από τον ηλεκτρικό, καθώς οι κλήσεις από το εσωτερικό του θαλάμου παίρνουν προτεραιότητα σε σχέση με όσες γίνονται από τους ορόφους. Επίσης, μπορεί να “επιλέξει” να εξυπηρετήσει πρώτα τον όροφο που βρίσκεται κοντύτερα στον παρόντα, παρά τον πιο μακρυνό. Έτσι, ο ηλεκτρονικός ανελκυστήρας λειτουργεί βάσει “προγράμματος”, το οποίο ξεπερνά σε υπολογιστική ισχύ ένα ΠΑ (χρειάζεται αυτόματο μεγαλύτερων υπολογιστικών δυνατοτήτων, από αυτά τα οποία θα συναντήσουμε σε επόμενες ενότητες). Γιαυτό εδώ θα παραμείνουμε στο παράδειγμα του ηλεκτρικού ανελκυστήρα.
Ας κάνουμε μια τροποποίηση στην ιδέα “ανελκυστήρας”. Ενώ κανονικά η δουλειά του ανελκυστήρα είναι να εξυπηρετεί (ατέρμονα, δίχως σταματημό) τους χρήστες, ας υποθέσουμε οτι έχουμε έναν ανελκυστήρα με ειδικό “σκοπό”: ο σκοπός-του είναι να φτάσει στο 2ο όροφο· όταν φτάσει εκεί, παύει να λειτουργεί. Έτσι, μπορούμε να πούμε οτι έχει μια τελική κατάσταση, την q2, την οποία θα συμβολίζουμε με διπλό κύκλο, όπως στο ακόλουθο διάγραμμα:
Εικ. 2.1.2: ΠΑ ανελκυστήρα με τελική κατάσταση q2
Επιπλέον παρατηρούμε οτι, χάρη στην τελική κατάσταση, το αυτόματο αυτό, ξεκινώντας από την αρχική κατάσταση q0, αποδέχεται την ακολουθία δεδομένων (δηλ. πατημάτων κουμπιών) 1010012, γιατί αφού ανταποκριθεί στα δεδομένα αυτά καταλήγει στην κατάσταση q2, που είναι τελική. Επομένως αποδέχεται τη συμβολοσειρά 1010012. Αντίθετα, απορρίπτει τη συμβολοσειρά 01011, γιατί αυτή δεν το οδηγεί στην τελική q2. Ας σημειωθεί οτι αποδέχεται επίσης τη συμβολοσειρά 00222, γιατί δεν είναι απαραίτητο να σταματήσει με το που θα βρεθεί σε τελική κατάσταση· σημασία για την αποδοχή ή απόρριψη έχει το σε ποια κατάσταση βρίσκεται το αυτόματο με την επεξεργασία και του τελευταίου δεδομένου εισόδου.
Ξεχνώντας για λίγο οτι το παραπάνω αυτόματο μοντελοποιεί έναν ανελκυστήρα, και βλέποντάς το κάπως αφηρημένα, θα μπορούσαμε να πούμε οτι αποδέχεται όλες τις συμβολοσειρές που τελειώνουν σε ένα ή περισσότερα 2, και απορρίπτει όλες τις υπόλοιπες.
Επομένως ένα αυτόματο μπορούμε να το δούμε σαν μηχανή που αποδέχεται ή απορρίπτει μια συμβολοσειρά δεδομένων εισόδου.
![]() Άσκηση 2.1.1:
Να κατασκευαστεί ο γράφος ενός ΠΑ το οποίο αποδέχεται όλες τις
συμβολοσειρές (και μόνο αυτές) που αποτελούνται από 0 και 1 και που
έχουν τουλάχιστον τρία διαδοχικά 1.
Άσκηση 2.1.1:
Να κατασκευαστεί ο γράφος ενός ΠΑ το οποίο αποδέχεται όλες τις
συμβολοσειρές (και μόνο αυτές) που αποτελούνται από 0 και 1 και που
έχουν τουλάχιστον τρία διαδοχικά 1.
![]() Άσκηση 2.1.2:
Να κατασκευαστεί ο γράφος ενός ΠΑ το οποίο αποδέχεται όλες τις
συμβολοσειρές (και μόνο αυτές) που αποτελούνται από 0 και 1 και που
έχουν άρτιο αριθμό από 0.
Άσκηση 2.1.2:
Να κατασκευαστεί ο γράφος ενός ΠΑ το οποίο αποδέχεται όλες τις
συμβολοσειρές (και μόνο αυτές) που αποτελούνται από 0 και 1 και που
έχουν άρτιο αριθμό από 0.
Άσκηση 2.1.3: Θεωρήστε τη λειτουργία ενός θερμοστάτη (π.χ. για αερόθερμο μπάνιου). Ο θερμοστάτης βάζει το μηχάνημα σε λειτουργία όταν η θερμοκρασία πέσει κάτω από ένα όριο, π.χ. τους 20°C, ενώ όταν η θερμοκρασία ξεπεράσει ένα άλλο όριο, π.χ. τους 25°C, τότε ο θερμοστάτης διακόπτει το ηλεκτρικό ρεύμα και σταματάει το μηχάνημα. Φτιάξτε ένα μοντέλο της λειτουργίας του θερμοστάτη ως ΠΑ με ένα γράφο. Κάντε την απλοποιητική υπόθεση οτι η θερμοκρασία μπορεί να είναι μόνο τριών ειδών: a = “κάτω των 20°C”, b = “μεταξύ 20°C και 25°C (περιλαμβανομένων των δύο ορίων)”, και c = “άνω των 25°C”. Αποφασίστε ποιες είναι οι καταστάσεις του θερμοστάτη (ας μην υπάρχει τελική κατάσταση), και πότε μεταφέρεται από τη μια κατάσταση στην άλλη.
Ορισμός:
ένα πεπερασμένο
αυτόματο (ΠΑ) είναι μια πεντάδα
(Q, Σ, δ, q0,
F), όπου: Q είναι ένα πεπερασμένο σύνολο καταστάσεων·
Σ
ένα πεπερασμένο αλφάβητο εισόδου· δ μια
συνάρτηση μετάβασης που απεικονίζει το Q
X
Σ → Q· το q0
![]() Q
λέγεται
αρχική κατάσταση· και το F ένα σύνολο
τελικών καταστάσεων.
Q
λέγεται
αρχική κατάσταση· και το F ένα σύνολο
τελικών καταστάσεων.
Η συνάρτηση μετάβασης δ (αγγλ.: transition function) προσδιορίζει σε ποια κατάσταση q' θα βρεθεί το αυτόματο για κάθε κατάσταση q και κάθε σύμβολο εισόδου a; ήτοι, δ(q, a) = q'.
Για παράδειγμα, το ΠΑ του ανελκυστήρα που συζητήθηκε νωρίτερα, έχει Q = {q0, q1, q2}, Σ = {0, 1, 2}, αρχική κατάσταση q0, F = {q2}, και μια δ που ορίζεται ως ακολούθως:
| δ | 0 | 1 | 2 |
| q0 | q0 | q1 | q2 |
| q1 | q0 | q1 | q2 |
| q2 | q0 | q1 | q2 |
Ορισμός: Τα αιτιοκρατικά πεπερασμένα αυτόματα (θα τα συντομογραφούμε ως ΑΠΑ), είναι αυτόματα όπως τα ανωτέρω, στα οποία κάθε κατάσταση και σύμβολο εισόδου αντιστοιχίζεται σε μία και μοναδική κατάσταση. (Στην επόμενη υποενότητα θα συναντήσουμε τα μη-αιτιοκρατικά ΠΑ.)
Αιτιοκρατία (αγγλ.: determinism) γενικά σε ένα φυσικό σύστημα σημαίνει οτι, έχοντας μια τρέχουσα κατάσταση και ένα δεδομένο εισόδου, γνωρίζουμε ή μπορούμε να μάθουμε σε ποια επόμενη κατάσταση θα βρεθεί το σύστημα αυτό. Μη-αιτιοκρατία (αγγλ.: nondeterminism) σημαίνει οτι δεν γνωρίζουμε συγκεκριμένα σε ποια κατάσταση θα βρεθεί, γιατί μπορεί να βρίσκεται σε ολόκληρο σύνολο καταστάσεων.
Η συνάρτηση μετάβασης δ μπορεί εύκολα να επεκταθεί σε μια συνάρτηση δ΄ ώστε η δ΄ να εφαρμόζει επί συμβολοσειρών αντί επί μεμονομένων συμβόλων, ως εξής:
-
δ΄(q, ε) = q
-
δ΄(q, wa) = δ (δ΄(q, w), a), για όλες τις συμβολοσειρές w και όλα τα σύμβολα εισόδου a.
Αν εφαρμόσουμε τη δ΄ σε ένα μεμονωμένο σύμβολο εισόδου a, παρατηρούμε οτι δ΄(q, a) = δ(q, a) (η αιτιολόγηση αυτού αφήνεται σαν άσκηση). Έτσι, καθώς δεν μπορεί να γίνει σύγχυση για το ποια από τις δύο συναρτήσεις, δ΄ ή δ, εννοείται (διακρίνονται λόγω του είδους της δεύτερης παραμέτρου-τους, που είναι συμβολοσειρά ή σύμβολο, αντιστοίχως), και καθώς τα αποτελέσματά τους σε μεμονωμένα σύμβολα είναι ταυτόσημα, θα πάψουμε να γράφουμε τη δ΄ και θα χρησιμοποιούμε τη δ, ακόμα και με συμβολοσειρές.
Ορισμός: μια συμβολοσειρά x
γίνεται αποδεκτή από ένα
πεπερασμένο αυτόματο M = (Q, Σ, δ,
q0,
F) αν
![]() p
p
![]() F:
δ(q0,
x) = p.
F:
δ(q0,
x) = p.
Αν η συμβολοσειρά δεν γίνεται αποδεκτή από το Μ, τότε λέμε οτι
απορρίπτεται από αυτό.
Ας σημειωθεί οτι ο παραπάνω ορισμός περιλαμβάνει όλα τα ΠΑ γενικά, και όχι μόνο τα ΑΠΑ.
Άσκηση 2.1.4: Δίνεται το αυτόματο που εικονίζεται* στο παρακάτω διάγραμμα:

Εικ. 2.1.3
Αποφασίστε αν το παραπάνω αυτόματο αποδέχεται τις συμβολοσειρές: 01, 001, 111010101, 000010101, και 1110101010.
![]() Άσκηση
2.1.5: Ο ορισμός ενός ΑΠΑ (του μόνου τύπου ΠΑ που έχουμε δει
μέχρι τώρα) απαιτεί οτι η συνάρτηση μετάβασης δ είναι ολική, δηλ.
ορίζεται για κάθε σύμβολο εισόδου σε κάθε κατάσταση. Θεωρήστε την
περίπτωση μιας μερικής δ, η οποία ορίζεται μεν για κάθε κατάσταση, αλλά
όχι απαραίτητα για κάθε σύμβολο εισόδου σε κάθε κατάσταση. Για
παράδειγμα, η δ που εμφανίζεται σε έναν πίνακα παραπάνω (στο “ΠΑ του
ανελκυστήρα”) θα μπορούσε να δίνεται ως εξής:
Άσκηση
2.1.5: Ο ορισμός ενός ΑΠΑ (του μόνου τύπου ΠΑ που έχουμε δει
μέχρι τώρα) απαιτεί οτι η συνάρτηση μετάβασης δ είναι ολική, δηλ.
ορίζεται για κάθε σύμβολο εισόδου σε κάθε κατάσταση. Θεωρήστε την
περίπτωση μιας μερικής δ, η οποία ορίζεται μεν για κάθε κατάσταση, αλλά
όχι απαραίτητα για κάθε σύμβολο εισόδου σε κάθε κατάσταση. Για
παράδειγμα, η δ που εμφανίζεται σε έναν πίνακα παραπάνω (στο “ΠΑ του
ανελκυστήρα”) θα μπορούσε να δίνεται ως εξής:
| δ | 0 | 1 | 2 |
| q0 | q0 | q2 | |
| q1 | q0 | q1 | |
| q2 | q1 | q2 |
(Αυτό θα αντιστοιχούσε σε έναν ανελκυστήρα με μερικά “χαλασμένα” κουμπιά.) Ας υποθέσουμε οτι τροποποιούμε τον ορισμό του ΑΠΑ ώστε να μπορεί να συμπεριλάβει και τις μερικές συναρτήσεις μετάβασης, ως εξής: αν το αυτόματο βρεθεί σε κατάσταση στην οποία το σύμβολο εισόδου δεν ορίζεται (π.χ., η κατάσταση q0 με το 1 σαν επόμενο σύμβολο εισόδου στο παραπάνω παράδειγμα) τότε το αυτόματο απορρίπτει τη συμβολοσειρά εισόδου. Δείξτε οτι μπορούμε πάντα να κατασκευάσουμε ένα ισοδύναμο* ΑΠΑ με μια ολική συνάρτηση δ το οποίο αποδέχεται και απορρίπτει ακριβώς τις ίδιες συμβολοσειρές με εκείνες που αποδέχεται και απορρίπτει το ΑΠΑ με τη μερική συνάρτηση δ. ▓
Ορισμός: η
γλώσσα που αναγνωρίζεται από
το πεπερασμένο αυτόματο Μ είναι το σύνολο των συμβολοσειρών: {x | δ(q0,
x)
![]() F}.
F}.
Ας σημειωθεί οτι ένα αυτόματο μπορεί να κάνει αποδεκτές πολλές συμβολοσειρές, αλλά αναγνωρίζει μόνο μία γλώσσα.
Ας σημειωθεί επίσης οτι ακόμα κι αν
ένα αυτόματο δεν αποδέχεται ούτε μία συμβολοσειρά, και πάλι αναγνωρίζει
μία γλώσσα:
![]() , την
κενή γλώσσα.
, την
κενή γλώσσα.
Θα χρησιμοποιούμε το συμβολισμό L(M) για να δηλώνουμε τη γλώσσα L που αναγνωρίζεται από το αυτόματο M.
![]() Άσκηση 2.1.6:
Απαριθμήστε λίγα ακόμα από τα στοιχεία της γλώσσας που αναγνωρίζεται από
το ΠΑ της άσκησης 2.1.4. Τώρα προσπαθήστε να δώσετε μια περιγραφή στα
ελληνικά όλων των συμβολοσειρών της γλώσσας εκείνης.
Άσκηση 2.1.6:
Απαριθμήστε λίγα ακόμα από τα στοιχεία της γλώσσας που αναγνωρίζεται από
το ΠΑ της άσκησης 2.1.4. Τώρα προσπαθήστε να δώσετε μια περιγραφή στα
ελληνικά όλων των συμβολοσειρών της γλώσσας εκείνης.
Ορισμός: μια γλώσσα λέγεται κανονικό σύνολο (αγγλ.: regular set) αν είναι η γλώσσα που αναγνωρίζεται από κάποιο πεπερασμένο αυτόματο. Μια τέτοια γλώσσα ονομάζεται επίσης κανονική γλώσσα (αγγλ.: regular language).
![]() Άσκηση
2.1.7: Θεωρήστε τη γλώσσα που αποτελείται από συμβολοσειρές οι
οποίες είναι οι δυαδικές αναπαραστάσεις μη αρνητικών ακεραίων n
τέτοιων ώστε n
Άσκηση
2.1.7: Θεωρήστε τη γλώσσα που αποτελείται από συμβολοσειρές οι
οποίες είναι οι δυαδικές αναπαραστάσεις μη αρνητικών ακεραίων n
τέτοιων ώστε n
![]() 1
mod 4 (δηλαδή αφήνουν υπόλοιπο 1
διαιρούμενοι διά 4). Είναι αυτή μια κανονική γλώσσα; Αν όχι, εξηγήστε
γιατί. Αν ναι, κατασκευάστε ένα ΠΑ που να την αναγνωρίζει.
1
mod 4 (δηλαδή αφήνουν υπόλοιπο 1
διαιρούμενοι διά 4). Είναι αυτή μια κανονική γλώσσα; Αν όχι, εξηγήστε
γιατί. Αν ναι, κατασκευάστε ένα ΠΑ που να την αναγνωρίζει.
2.2
Μη-αιτιοκρατικά Πεπερασμένα ΑυτόματαΝωρίτερα μιλήσαμε για την αιτιοκρατία στα ΠΑ, που σημαίνει οτι έχοντας μια κατάσταση q και ένα σύμβολο εισόδου a, υπάρχει μόνο ένα βέλος που φεύγει από την q και είναι σημειωμένο με το a. (Με άλλα λόγια, η συνάρτηση μετάβασης δ είναι μια αληθινή συνάρτηση.) Χρησιμοποιήσαμε το ακρόστιχο “ΑΠΑ” για τα αιτιοκρατικά ΠΑ. Τώρα θα συναντήσουμε τα μη-αιτιοκρατικά ΠΑ (“ΜΠΑ”) στα οποία, όταν δίνεται μια κατάσταση q και ένα σύμβολο εισόδου a, μπορεί να υπάρχουν περισσότερα από ένα βέλη που να φεύγουν από την q και να έχουν ετικέτα a. Σε μια τέτοια περίπτωση, το ΜΠΑ περνά όχι σε μια και μοναδική κατάσταση, αλλά σε όλες τις καταστάσεις που είναι προσβάσιμες από την q με βέλη που έχουν ετικέτα a. Με άλλα λόγια, η δ δεν είναι πλέον συνάρτηση μετάβασης, αλλά μια απεικόνιση πολλαπλών τιμών (αγγλ.: mapping), που απεικονίζει την q σε ένα σύνολο διαδόχων καταστάσεων.
Ένας άλλος τρόπος για να δούμε τη λειτουργία ενός ΜΠΑ είναι οτι κάθε φορά που το αυτόματο συναντά n επιλογές για κάθε σύμβολο εισόδου σε μια κατάσταση, “διαχωρίζεται” σε n αντίγραφα του εαυτού-του, και κάθε αντίγραφο συνεχίζει να δουλεύει με τα στοιχεία εισόδου ανεξάρτητα από τα άλλα αντίγραφα. Φυσικά, ο διαχωρισμός αυτός μπορεί να συμβεί πάλι: αν ένα από τα αντίγραφα συναντήσει m επιλογές, διαχωρίζεται εκ νέου σε m επιλογές, καθεμία από τις οποίες προχωρά ανεξάρτητα από όποια άλλα αντίγραφα έχουν δημιουργηθεί μέχρι τότε. Οι φυσικοί πρέπει να είναι εξοικειωμένοι με αυτόν τον τρόπο λειτουργίας των ΜΠΑ, που θυμίζει την κβαντομηχανική “ερμηνεία πολλαπλών κόσμων”, του Hugh Everett.
Πότε μπορεί να αποδεχτεί ένα ΜΠΑ την είσοδο; Μπορεί όταν οποιοδήποτε από τα αντίγραφά του (που λειτουργούν ανεξάρτητα) φτάσει σε τελική κατάσταση.*
Το παρακάτω είναι παράδειγμα ενός ΜΠΑ:

Εικ. 2.2.1: Παράδειγμα ενός ΜΠΑ
Το παραπάνω ΜΠΑ αποδέχεται όλες τις συμβολοσειρές με 0 ή 1 που τελειώνουν είτε σε 00, είτε σε 11. Είναι μη-αιτιοκρατικό γιατί στην κατάσταση q0 με το στοιχείο εισόδου 0 έχει δύο επιλογές: είτε να μείνει στην κατάσταση q0, είτε να αλλάξει στην q1. Το ίδιο ισχύει και με το σύμβολο εισόδου 1, αλλά η ύπαρξη μιας και μόνο πολλαπλής επιλογής αρκεί για να χαρακτηρίσει ένα ΠΑ σαν ΜΠΑ.
![]() Άσκηση 2.2.1:
Χρησιμοποιώντας το προηγούμενο παράδειγμα σαν οδηγό, κατασκευάστε τον
γράφο ενός ΜΠΑ που αποδέχεται όλες τις ελληνικές λέξεις που τελειώνουν
σε “-ωρ” και μόνο αυτές. (Μπορείτε να χρησιμοποιήσετε συντομογραφία για
να αποφύγετε να ζωγραφίσετε από ένα βέλος για κάθε γράμμα του
αλφαβήτου.) Τώρα σκεφτείτε πώς θα έπρεπε να κατασκευαστεί ο γράφος σαν
ΑΠΑ. Τί παρατηρείτε;
Άσκηση 2.2.1:
Χρησιμοποιώντας το προηγούμενο παράδειγμα σαν οδηγό, κατασκευάστε τον
γράφο ενός ΜΠΑ που αποδέχεται όλες τις ελληνικές λέξεις που τελειώνουν
σε “-ωρ” και μόνο αυτές. (Μπορείτε να χρησιμοποιήσετε συντομογραφία για
να αποφύγετε να ζωγραφίσετε από ένα βέλος για κάθε γράμμα του
αλφαβήτου.) Τώρα σκεφτείτε πώς θα έπρεπε να κατασκευαστεί ο γράφος σαν
ΑΠΑ. Τί παρατηρείτε;
Ορισμός: ένα μη-αιτιοκρατικό πεπερασμένο αυτόματο (ΜΠΑ) είναι μια πεντάδα M = (Q, Σ, δ, q0, F), όπου τα Q, Σ, q0, και F έχουν το ίδιο νόημα όπως και στον ορισμό του ΑΠΑ, αλλά το δ είναι μια απεικόνιση: Q X Σ → P (Q), όπου το P (Q) είναι το δυναμοσύνολο του Q (το σύνολο όλων των υποσυνόλων του Q).
Όπως και με τα ΑΠΑ, η απεικόνιση μετάβασης δ μπορεί να επεκταθεί ώστε να δέχεται συμβολοσειρές αντί για μεμονωμένα στοιχεία εισόδου, κατά παρόμοιο τρόπο (οι τυπικές λεπτομέρειες αφήνονται σαν άσκηση). Έτσι, μπορούμε να γράψουμε: δ: Q X Σ* → P (Q). Επιπρόσθετα όμως, εδώ είναι χρήσιμο να επεκτείνουμε τη δ και έτσι ώστε να δέχεται σύνολα καταστάσεων, αντί για μεμονωμένες καταστάσεις: δ: P (Q) X Σ* → P (Q). Αυτή η τελευταία επέκταση γίνεται ως εξής:
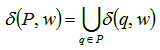
![]() P
P![]() Q.
Έτσι μπορούμε να μιλάμε και πάλι για την L(M), τη γλώσσα που
αναγνωρίζεται από το ΜΠΑ M, που είναι η:
Q.
Έτσι μπορούμε να μιλάμε και πάλι για την L(M), τη γλώσσα που
αναγνωρίζεται από το ΜΠΑ M, που είναι η:
L(M) = {w | δ(q0,
w) περιέχει μια κατάσταση q
![]() F}.
F}.
2.3
Ισοδυναμία μεταξύ ΑΠΑ και ΜΠΑΔιαισθητικά, ένα ΜΠΑ μοιάζει να είναι “ικανότερο” από ένα ΑΠΑ· ήτοι, να μπορεί να αναγνωρίσει περισσότερες γλώσσες, γιατί μπορεί να προσομοιώσει ένα ΑΠΑ (με την έννοια οτι κάθε ΑΠΑ είναι ένα ΜΠΑ το οποίο στην απεικόνιση μετάβασής του, δ, τυχαίνει να μην έχει περισσότερες από μια καταστάσεις–διαδόχους δοσμένης μιας κατάστασης και ενός συμβόλου εισόδου). Όμως, όπως θα δούμε αμέσως, αυτή η διαίσθηση αποδεικνύεται λανθασμένη: τα ΜΠΑ αναγνωρίζουν ακριβώς τις ίδιες γλώσσες όπως και τα ΑΠΑ, δηλαδή τις κανονικές γλώσσες. Αυτό δηλώνεται στο ακόλουθο θεώρημα:
Θεώρημα 2.3.1: μια γλώσσα L αναγνωρίζεται από ένα ΜΠΑ αν και μόνο αν αναγνωρίζεται από ένα ΑΠΑ.
|
Απόδειξη. Η κατεύθυνση “αν” του θεωρήματος είναι προφανής: αν η γλώσσα L είναι κανονική, δηλαδή αναγνωρίζεται από ένα ΑΠΑ, τότε το ίδιο ΑΠΑ μπορεί να θεωρηθεί σαν ΜΠΑ, μετατρέποντας κάθε κατάσταση q του ΑΠΑ στο μοναδιαίο σύνολο {q}, που είναι η αντίστοιχη κατάσταση του ΜΠΑ. Η κατεύθυνση “και μόνο αν” είναι λίγο δυσκολότερη στην απόδειξη, αλλά βασίζεται στην απλή ιδέα οτι, δοσμένου ενός ΜΠΑ το οποίο αναγνωρίζει την L, μπορούμε να κατασκευάσουμε ένα ΑΠΑ που αναγνωρίζει την ίδια L “προσομοιώνοντας” τη λειτουργία του ΜΠΑ σε κάθε χρονική στιγμή, αντιστοιχίζοντας σύνολα καταστάσεων του ΜΠΑ σε καταστάσεις του ΑΠΑ. Δηλαδή, παίρνοντας ένα στιγμιότυπο του ΜΠΑ σε μια χρονική στιγμή, θεωρώντας όλες τις καταστάσεις στις οποίες βρίσκεται κάθε “παράλληλο αντίγραφο” του ΜΠΑ, και βάζοντας αυτές τις καταστάσεις σε ένα σύνολο {q1, ..., qi}, θα πούμε οτι αυτό το σύνολο αντιστοιχεί σε μια μόνο κατάσταση του ισοδύναμου ΑΠΑ. Ας κάνουμε αυτή την ιδέα πιο συγκεκριμένη. Έστω οτι το M = (Q, Σ, δ, q0, F) είναι ένα ΜΠΑ που αναγνωρίζει την L. Θα κατασκευάσουμε το ΑΠΑ M΄ = (Q΄, Σ, δ΄, q0΄, F΄), ισοδύναμο του Μ, ως εξής. Οι καταστάσεις του M΄
είναι όλα τα υποσύνολα των καταστάσεων του Μ. Δηλαδή,
Q΄ =
P
(Q). (Συνήθως μόνο ένα υποσύνολο,
και όχι όλες εκείνες οι καταστάσεις θα χρησιμοποιηθούν από το ΑΠΑ·
εντούτοις, εν δυνάμει μπορεί να είναι όλες οι
2|Q|
καταστάσεις.) Το
F΄ είναι το σύνολο όλων των καταστάσεων του
Q΄ που περιέχουν μία q
δ΄([q1,
q2,
...,
qi],
a) = [p1,
p2,
..., pj]
(Το “ Είναι εύκολο να δείξουμε με επαγωγή επί του μήκους της συμβολοσειράς x οτι: δ΄(q0΄,
x) = [q1,
q2,
...,
qi]
Επαγωγική βάση:
για |
x
| = 0 (δηλ. x = ε)
έχουμε τετριμμένα οτι
δ΄(q0΄, ε)
= [q0]
Επαγωγικό βήμα:
έστω οτι η υπόθεση ισχύει για εισόδους μήκους
n ή μικρότερου.
Έστω οτι το xa
είναι μια συμβολοσειρά που έχει
μήκος n + 1, με a
δ΄(q0΄, xa) = δ΄(δ΄(q0΄, x), a). Από την επαγωγική υπόθεση,
δ΄(q0΄,
x) = [p1,
p2,
..., pj]
Αλλά από τον ορισμό της δ΄, δ΄([p1,
p2,
..., pj],
a) = [r1,
r2,
..., rk]
Οπότε, δ΄(q0΄,
xa) = [r1,
r2,
..., rk]
πράγμα που ολοκληρώνει το επαγωγικό βήμα. Για να είναι η απόδειξη
πλήρης, πρέπει να προσθέσουμε οτι η δ΄(q0΄,
x)
|
![]() Άσκηση 2.3.1:
Θεωρήστε το ΜΠΑ που εικονίζεται στον ακόλουθο γράφο:
Άσκηση 2.3.1:
Θεωρήστε το ΜΠΑ που εικονίζεται στον ακόλουθο γράφο:
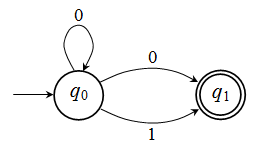
Εικ. 2.3.1
Αυτό το ΜΠΑ κάνει αποδεκτές όλες τις συμβολοσειρές με πρόθεμα μηδέν ή περισσοτέρων 0 και με κατάληξη το 0 ή το 1. Κάνοντας χρήση της απόδειξης του παραπάνω θεωρήματος 2.3.1, κατασκευάστε ένα ΑΠΑ που να είναι ισοδύναμο με αυτό το ΜΠΑ. Πριν καν ξεκινήσετε, απαντήστε την ερώτηση: ποιο είναι το σύνολο F΄ του ισοδύναμου ΑΠΑ; ▓
Ποια η χρησιμότητα των ΜΠΑ; Εκτός του οτι μας είναι χρήσιμα σαν εισαγωγή στην έννοια της μη αιτιοκρατίας, έχουν και μια εγγενή χρησιμότητα: απλοποιούν τη δομή του αυτομάτου, σε πολλές περιπτώσεις, όπως φαίνεται στην επόμενη άσκηση.
![]() Άσκηση 2.3.2: Προσπαθήστε να εκφράσετε το ΑΠΑ της άσκησης
2.3.1 με όσο το δυνατόν μικρότερο αριθμό καταστάσεων. Υπόδειξη: θα διαπιστώσετε
οτι δεν υλοποιείται με αριθμό καταστάσεων < 3.
▓
Άσκηση 2.3.2: Προσπαθήστε να εκφράσετε το ΑΠΑ της άσκησης
2.3.1 με όσο το δυνατόν μικρότερο αριθμό καταστάσεων. Υπόδειξη: θα διαπιστώσετε
οτι δεν υλοποιείται με αριθμό καταστάσεων < 3.
▓
Τα ΜΠΑ είναι επίσης χρήσιμα βοηθώντας-μας να καταλάβουμε οτι η προσθήκη μιας φαινομενικά “έξτρα ικανότητας” στο αυτόματο (όπως η ικανότητα να μεταφέρεται σε πολλαπλές καταστάσεις με ένα σύμβολο εισόδου) δεν προσθέτει τίποτα στην υπολογιστική ικανότητα του αυτομάτου. Όταν θα εξετάσουμε τον πιο ισχυρό τύπο αυτομάτων, δηλαδή τις Μηχανές Τούρινγκ, θα διαπιστώσουμε οτι το ίδιο ισχύει και εκεί, δηλαδή η μη-αιτιοκρατία δεν αυξάνει την υπολογιστική ικανότητα. Τώρα θα προσθέσουμε άλλη μια ικανότητα στα ΜΠΑ.
2.4 ΜΠΑ με μεταβάσεις-ε
Στις προηγούμενες υποενότητες (§2.2 και §2.3) είδαμε οτι προσθέτοντας μια επιπλέον “ικανότητα” στα αιτιοκρατικά αυτόματα (ΑΠΑ), ήτοι μετατρέποντάς τα σε μη-αιτιοκρατικά (ΜΠΑ), δεν μεγάλωσε το σύνολο των αναγνωρίσιμων γλωσσών. Ας προσθέσουμε τώρα μια επιπλέον ικανότητα στα ΜΠΑ, για να δούμε αν το σύνολο των αναγνωρίσιμων γλωσσών θα μεγαλώσει.
Επεκτείνουμε λοιπόν το μοντέλο των ΜΠΑ ώστε αυτά να περιλαμβάνουν και “κενές μεταβάσεις”, δηλαδή μεταβάσεις οι οποίες να πραγματοποιούνται χωρίς στοιχείο εισόδου· ή, ισοδύναμα, να πραγματοποιούνται με την κενή συμβολοσειρά ε. Τις μεταβάσεις αυτές θα τις λέμε “μεταβάσεις-ε”, και τα αυτόματα που περιλαμβάνουν μία ή περισσότερες μεταβάσεις-ε θα τα λέμε ΜΠΑ-ε. Πριν να δώσουμε τον ορισμό, ας δούμε ένα παράδειγμα, εξετάζοντας το ακόλουθο ΜΠΑ-ε.
Εικ. 2.4.1: Παράδειγμα ενός ΜΠΑ-ε
Το παραπάνω αυτόματο, από την κατάσταση q0 μεταφέρεται στην κατάσταση q1 με ένα ή περισσότερα 0 στην είσοδο. Αλλά όταν πλέον βρίσκεται στην κατάσταση q1, τότε μπορεί να μεταφερθεί στην κατάσταση q2 (που είναι τελική) ακόμα και χωρίς να επεξεργαστεί κάποιο στοιχείο εισόδου. Με άλλα λόγια, μετά από ένα ή περισσότερα μηδενικά, μπορεί να πάει κατευθείαν σε τελική κατάσταση και να αποδεχτεί τη συμβολοσειρά εισόδου, η οποία μπορεί να περιλαμβάνει (προαιρετικά) και κάποια 1 στη σειρά, ή και (επίσης προαιρετικά) κάποια 2 στη σειρά.
Ας ορίσουμε τώρα “επίσημα” τα ΜΠΑ-ε.
Ορισμός: Ένα
μη-αιτιοκρατικό αυτόματο με μεταβάσεις-ε
(ΜΠΑ-ε) είναι μια πεντάδα M = (Q, Σ, δ,
q0,
F), όπου τα Q, Σ, q0,
και F έχουν το ίδιο νόημα όπως και στον ορισμό των ΜΠΑ, αλλά η
απεικόνιση δ τώρα είναι: Q
X
(Σ
![]() {ε}) →
P
(Q). (Και πάλι,
P
(Q) είναι το δυναμοσύνολο του Q.)
{ε}) →
P
(Q). (Και πάλι,
P
(Q) είναι το δυναμοσύνολο του Q.)
Συνεπώς στα ΜΠΑ-ε η δ επιτρέπει τη μετάβαση από κατάσταση σε κατάσταση μέσω είτε συμβόλου από το Σ, είτε “κανενός συμβόλου”, δηλαδή του κενού ε.
Σκοπός-μας τώρα είναι να δείξουμε οτι όποια συμβολοσειρά γίνεται αποδεκτή από ένα ΜΠΑ-ε, γίνεται επίσης αποδεκτή από ένα ΜΠΑ. Για να το πετύχουμε αυτό, θα βοηθηθούμε κάνοντας τα εξής:
-
Ορίζοντας μια νέα συνάρτηση, την “κλειστότητα-ε”, επί καταστάσεων, και
-
Επεκτείνοντας την απεικόνιση δ ώστε να απεικονίζει σύνολα καταστάσεων και ολόκληρες συμβολοσειρές στο P (Q).
Ας δούμε πρώτα την κλειστότητα-ε.
Ορισμός: Έστω μια κατάσταση q ενός αυτομάτου. Η κλειστότητα-ε (q) είναι το σύνολο των καταστάσεων στις οποίες μπορεί να φτάσει το αυτόματο από την q μέσω μεταβάσεων-ε.
Ασφαλώς στην κλειστότητα-ε (q) περιλαμβάνεται η q γιατί, κατά τετριμμένο τρόπο, το αυτόματο “φτάνει” από την q στην q χωρίς να χρησιμοποιήσει κανένα σύμβολο εισόδου, άρα με το κενό ε. Οπότε η κλειστότητα-ε δεν είναι ποτέ το κενό σύνολο.
Παράδειγμα: στο παραπάνω ΜΠΑ-ε, έχουμε: κλειστότητα-ε (q0) = {q0}, αλλά κλειστότητα-ε (q1) = {q1, q2}.
Προφανώς, ο παραπάνω ορισμός επεκτείνεται κατά φυσικό τρόπο ώστε να εφαρμόζει σε σύνολα καταστάσεων, και όχι σε μία μόνο κατάσταση:
| Ορισμός: αν Q είναι ένα σύνολο καταστάσεων, τότε κλειστότητα-ε (Q) = |
|
κλειστότητα-ε (q) |
Όλα αυτά θα τα χρησιμοποιήσουμε σε λίγο. Προς το παρόν ας κάνουμε και τη δεύτερη επέκταση, αυτήν που αφορά στη δ.
Ορισμός: Αν δ είναι μια
απεικόνιση Q
X
(Σ
![]() {ε}) →
P
(Q), δηλαδή όπως ορίστηκε στα ΜΠΑ-ε τότε η
δ΄: Q
X
Σ* →
P
(Q) ορίζεται ως εξής:
{ε}) →
P
(Q), δηλαδή όπως ορίστηκε στα ΜΠΑ-ε τότε η
δ΄: Q
X
Σ* →
P
(Q) ορίζεται ως εξής:
-
δ΄(q, ε) = κλειστότητα-ε (q).
-
Για κάθε x
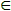 Σ*
και a
Σ*
και a
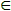 Σ,
δ΄(q, xa) = κλειστότητα-ε
(Q), όπου Q = {p | για κάποιο
r
Σ,
δ΄(q, xa) = κλειστότητα-ε
(Q), όπου Q = {p | για κάποιο
r
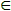 δ΄(q,
x), p
δ΄(q,
x), p
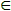 δ(r,
a)}.
δ(r,
a)}.
Η 2η συνθήκη του παραπάνω ορισμού λέει: για να βρούμε το αποτέλεσμα της δ΄επί μιας συμβολοσειράς w σε δεδομένη κατάσταση q, αναλύουμε τη w σε xa, όπου το a είναι το τελευταίο σύμβολο της w, και βρίσκουμε το σύνολο των καταστάσεων p στις οποίες μπορούμε να καταλήξουμε από καταστάσεις r μέσω του συμβόλου a, όπου οι r προέκυψαν από εφαρμογή (αναδρομικά) της δ΄ πάνω στο x ξεκινώντας από την q. Το x φυσικά είναι μικρότερο σε μήκος από το w, οπότε αυτός ο ορισμός αναδρομικά θα καταλήξει κάποτε στη συνθήκη 1, τη “βάση” του ορισμού. Τέτοιους αναδρομικούς ορισμούς θα συναντάμε αρκετά συχνά στο εξής.
Παρομοίως τώρα, οι δ και δ΄ μπορούν να επεκταθούν σε σύνολα καταστάσεων. Θα χρησιμοποιήσουμε τα ίδια σύμβολα, δ και δ΄:
| 3. δ(Q, a) = |
|
δ(q, a), και |
| 4. δ΄(Q, x) = |
|
δ΄(q, x) |
όπου Q είναι ένα σύνολο καταστάσεων, όπως και πριν.
Ας σημειωθεί οτι οι δ(q, a) και δ΄(q, a) δεν ταυτίζονται κατ’ ανάγκη, γιατί η δ(q, a) περιλαμβάνει μόνο το σύνολο καταστάσεων p που ενώνονται με την q μέσω ακμών σημειωμένων με το a, ενώ η δ΄(q, a) περιλαμβάνει το σύνολο των καταστάσεων p οι οποίες είτε ενώνονται με την q μέσω ακμών σημειωμένων με το a (όπως για τη δ), είτε για τις οποίες υπάρχει διαδρομή από το q στο p μέσω ακμών σημειωμένων με το ε, διαδρομή που περιλαμβάνει πιθανώς και (το πολύ) μια ακμή σημειωμένη με το a.
Ορισμός: Η
γλώσσα L(M) που
γίνεται αποδεκτή από το αυτόματο Μ = (Q, Σ, δ,
q0,
F) είναι το εξής σύνολο συμβολοσειρών x:
{x | η δ΄(q0,
x) περιλαμβάνει μια κατάσταση στο
F}.
Με άλλα λόγια, η γλώσσα L που αποδέχεται ένα αυτόματο M είναι το σύνολο των συμβολοσειρών για τις οποίες το M ξεκινάει από αρχική κατάσταση και καταλήγει σε τελική κατάσταση, αφού “διαβάσει” ολόκληρη τη συμβολοσειρά (πιθανώς κάνοντας και κάποιες μεταβάσεις-ε).
Μπορούμε τώρα να δείξουμε πως τα ΜΠΑ-ε μπορούν να προσομοιωθούν από τα ΜΠΑ· δηλαδή τα ΜΠΑ-ε δεν προσθέτουν κάτι σε “υπολογιστική ισχύ”:
Θεώρημα 2.4.1: Αν η γλώσσα L γίνεται αποδεκτή από ένα ΜΠΑ-ε, τότε η L γίνεται επίσης αποδεκτή από ένα ΜΠΑ (χωρίς μεταβάσεις-ε).
|
Απόδειξη. Έστω Μ = (Q, Σ, δ, q0, F) ένα ΜΠΑ-ε. Θα κατασκευάσουμε ένα Μ΄ = (Q, Σ, ζ, q0, F΄), όπου:
και η ζ(q,
a) = δ΄(q,
a), όπως ορίστηκε παραπάνω η δ΄, δηλαδή ως
επέκταση της δ(q, a), για
q
Ας σημειωθεί οτι το Μ΄ δεν θα έχει μεταβάσεις-ε (θα είναι δηλαδή ΜΠΑ), επομένως οι ζ και ζ΄ ταυτίζονται για το Μ΄, οπότε θα χρησιμοποιούμε μόνο το ζ· αλλά οι δ και δ΄ είναι διαφορετικές (αφού το Μ είναι ΜΠΑ-ε), άρα θα διαφοροποιούμε αυτές τις δύο. Πρώτα θέλουμε να δείξουμε με επαγωγή στο μήκος του |x| οτι ζ(q0, x) = δ΄(q0, x). Εντούτοις, αν x = ε αυτό μπορεί να μην ισχύει, καθώς ζ(q0, ε) = {q0}, ενώ δ΄(q0, ε) = κλειστότητα-ε (q0), που εν γένει διαφέρει από το {q0}. Επομένως αρχίζουμε την επαγωγική βάση από το μήκος |x| = 1. Επαγωγική βάση: Αν |x| = 1, τότε το x είναι ένα σύμβολο a, και ζ(q0, a) = δ΄(q0, a) εξ ορισμού της ζ. Επαγωγικό βήμα: Υποθέτουμε |x|
> 1. Έστω x = wa για κάποιο σύμβολο
a
ζ(q0, wa) = ζ(ζ(q0, w), a). Από την επαγωγική υπόθεση, ζ(q0, w) = δ΄(q0, w). Έστω οτι δ΄(q0, w) = Q. Πρέπει να δείξουμε οτι ζ(Q, a) = δ(q0, wa). Όμως έχουμε:
Οπότε, καθώς Q = δ΄(q0, w), έχουμε:
λόγω του κανόνα (2) στον ορισμό της δ΄. Οπότε, ζ(q0, wa) = δ΄(q0, wa). Πρέπει τώρα να δείξουμε οτι η ζ(q0,
x) περιλαμβάνει μια κατάσταση του
F΄ αν και μόνο αν η δ΄(q0,
x) περιλαμβάνει μια κατάσταση του
F. Αν x =
ε, αυτό έπεται αμέσως από τον ορισμό της F΄,
διότι ζ(q0,
ε) = {q0},
και η q0
ανήκει στο F΄ οποτεδήποτε η δ΄(q0,
ε) — που είναι η κλειστότητα-ε (q0)
— περιλαμβάνει μια κατάσταση (πιθανώς την q0)
στο F. Αν τώρα x
|
![]() Άσκηση 2.4.1:
Χρησιμοποιώντας τις ιδέες της απόδειξης του παραπάνω θεωρήματος,
προσπαθήστε να κατασκευάσετε ένα ΜΠΑ που να είναι ισοδύναμο (να
αναγνωρίζει ακριβώς την ίδια γλώσσα) με εκείνο της
Εικ. 2.4.1.
Άσκηση 2.4.1:
Χρησιμοποιώντας τις ιδέες της απόδειξης του παραπάνω θεωρήματος,
προσπαθήστε να κατασκευάσετε ένα ΜΠΑ που να είναι ισοδύναμο (να
αναγνωρίζει ακριβώς την ίδια γλώσσα) με εκείνο της
Εικ. 2.4.1.
![]() Άσκηση 2.4.2:
Στο ΜΠΑ-ε της Εικ.
2.4.1, αλλάξτε τη συνθήκη οτι πρέπει “να υπάρχουν ένα ή
περισσότερα 0 στην είσοδο”, και κάνετέ την “να υπάρχουν μηδέν ή
περισσότερα 0 στην είσοδο”, δηλαδή και τα 0 να είναι προαιρετικά (όπως
και τα 1 και τα 2). Κατασκευάστε το ΜΠΑ-ε που αποδέχεται αυτήν
ακριβώς τη γλώσσα, δηλαδή: έναν προαιρετικό αριθμό από 0, ακολουθούμενο
από έναν προαιρετικό αριθμό από 1, ακολουθούμενο από έναν προαιρετικό
αριθμό από 2. Κάντε το αυτόματο αυτό να έχει οπωσδήποτε μία ή
περισσότερες μεταβάσεις-ε (να είναι δηλαδή “γνήσιο ΜΠΑ-ε”),
και μόνο μία τελική κατάσταση.
Άσκηση 2.4.2:
Στο ΜΠΑ-ε της Εικ.
2.4.1, αλλάξτε τη συνθήκη οτι πρέπει “να υπάρχουν ένα ή
περισσότερα 0 στην είσοδο”, και κάνετέ την “να υπάρχουν μηδέν ή
περισσότερα 0 στην είσοδο”, δηλαδή και τα 0 να είναι προαιρετικά (όπως
και τα 1 και τα 2). Κατασκευάστε το ΜΠΑ-ε που αποδέχεται αυτήν
ακριβώς τη γλώσσα, δηλαδή: έναν προαιρετικό αριθμό από 0, ακολουθούμενο
από έναν προαιρετικό αριθμό από 1, ακολουθούμενο από έναν προαιρετικό
αριθμό από 2. Κάντε το αυτόματο αυτό να έχει οπωσδήποτε μία ή
περισσότερες μεταβάσεις-ε (να είναι δηλαδή “γνήσιο ΜΠΑ-ε”),
και μόνο μία τελική κατάσταση.
2.
5 Κανονικές εκφράσειςΌλες οι γλώσσες που γίνονται αποδεκτές από τα ΠΑ τα οποία έχουμε συναντήσει μέχρι στιγμής μπορούν να περιγραφούν από παραστάσεις που θα τις λέμε “κανονικές εκφράσεις”, οι οποίες θα μας δώσουν ένα συνοπτικό τρόπο αναπαράστασης κάθε κανονικής γλώσσας.
Στην εισαγωγή είχαμε ορίσει τη συνένωση δύο συμβολοσειρών. Εδώ μπορούμε να ορίσουμε τη συνένωση δύο γλωσσών:
Ορισμός: Έστω Σ ένα αλφάβητο,
και L1
και L2 δύο
γλώσσες από το Σ. Η συνένωση των
L1
και L2,
που θα τη συμβολίζουμε L1L2,
είναι η γλώσσα {xy | x
![]() L1
και y
L1
και y
![]() L2},
δηλαδή αυτή που προκύπτει παίρνοντας συμβολοσειρές από την
L1
και την L2
καθ’ όλους τους δυνατούς τρόπους, και σχηματίζοντας τη συνένωσή τους.
L2},
δηλαδή αυτή που προκύπτει παίρνοντας συμβολοσειρές από την
L1
και την L2
καθ’ όλους τους δυνατούς τρόπους, και σχηματίζοντας τη συνένωσή τους.
Θα χρισιμοποιούμε το συμβολισμό Ln για τη γλώσσα της συνένωσης LLn–1, όπου n > 0, και L0 = {ε}.
Δεδομένων των παραπάνω, θυμίζουμε το συμβολισμό L* για την κλειστότητα Κλέινι, που επίσης ορίστηκε στην εισαγωγή.
Ορισμός: Θα ορίσουμε επίσης τη θετική κλειστότητα της L, συμβολιζόμενη με το L+, που είναι το ίδιο οπως η L*, εξαιρώντας όμως την περίπτωση της “συνένωσης” με την κενή συμβολοσειρά. Αλλά προσοχή: αν η L περιλαμβάνει την κενή συμβολοσειρά ε, τότε (και μόνο τότε) και η L+ περιλαμβάνει την ε.
Βάσει όλων αυτών, μπορούμε τώρα να ορίσουμε τις κανονικές εκφράσεις.
Ορισμός: Έστω Σ ένα αλφάβητο. Οι κανονικές εκφράσεις (Κ.Ε.) από το Σ είναι σύνολα που ορίζονται αναδρομικά ως εξής:
-
Το
 είναι κανονική έκφραση.
είναι κανονική έκφραση. -
Το {ε} είναι κανονική έκφραση, και συμβολίζεται με το ε (με έντονη γραφή).
-
Για κάθε a
 Σ, το {a} είναι κανονική έκφραση, που θα
συμβολίζουμε με a (με έντονη
γραφή).
Σ, το {a} είναι κανονική έκφραση, που θα
συμβολίζουμε με a (με έντονη
γραφή). -
Αν r και s είναι κανονικές εκφράσεις που δηλώνουν τα σύνολα R και S αντιστοίχως, τότε τα (r + s), (rs), και (r*) είναι κανονικές εκφράσεις που δηλώνουν τα σύνολα R
 S, RS,
και R*,
αντιστοίχως.
S, RS,
και R*,
αντιστοίχως.
Θα συμβολίζουμε με r+ το rr*.
Επίσης, προφανώς (r
+ s) = (s
+ r), αφού
R
![]() S =
S
S =
S
![]() R. Αν δηλαδή δούμε το + ως πράξη
συνόλων (η ένωση συνόλων), τότε το + έχει τη συμμετρική ιδιότητα.
Όμως η συνένωση δεν έχει τη συμμετρική ιδιότητα.
R. Αν δηλαδή δούμε το + ως πράξη
συνόλων (η ένωση συνόλων), τότε το + έχει τη συμμετρική ιδιότητα.
Όμως η συνένωση δεν έχει τη συμμετρική ιδιότητα.
Παραδείγματα: Έστω το αλφάβητο Σ = {a, b}. Τότε τα παρακάτω είναι Κ.Ε.:
-
Το b, δηλαδή το σύνολο {b}.
-
Το ε, δηλαδή το σύνολο της κενής συμβολοσειράς {ε}.
-
Τα (ab) και (ba), δηλαδή τα σύνολα {ab} και {ba}, αντιστοίχως.
-
Το (a+b), δηλαδή το σύνολο {a, b}.
-
Το ((ba)+a), δηλαδή το σύνολο {a, ba}.
-
Το (a*), δηλαδή το σύνολο {ε, a, aa, aaa, ...}.
-
Το ((a+b)*), δηλαδή το σύνολο οποιασδήποτε ακολουθίας αποτελούμενης από a και b, με οποιαδήποτε σειρά.
-
Το ((bab)(a+b)*), δηλαδή το σύνολο των συμβολοσειρών με πρόθεμα bab και κατάληξη ((a+b)*)(βλ. προηγούμενο).
-
Το (((ab)+(a+b)*)(ba)*), δηλαδή το σύνολο των συμβολοσειρών με πρόθεμα οποιαδήποτε ακολουθία από ένα ή περισσότερα ab, ακολουθούμενη από ((a+b)*), και με κατάληξη μια προαιρετική ακολουθία από ba.
Ορίζουμε την προτεραιότητα των πράξεων της ένωσης (+), συνένωσης, και κλειστοτήτων (Κλέινι και θετικής) σε μια Κ.Ε. ως εξής;
-
Την υψηλότερη προτεραιότητα έχει το ζεύγος των παρενθέσεων·
-
την αμέσως επόμενη προτεραιότητα έχουν οι κλειστότητες (Κλέινι και θετική)·
-
έπεται σε προτεραιότητα η συνένωση·
-
και τη χαμηλότερη προτεραιότητα έχει η ένωση.
Βάσει των προτεραιοτήτων, όταν οι παρενθέσεις δεν είναι απαραίτητες θα τις παραλείπουμε. Έτσι, την παράσταση ((bab)(a+b)*) (προτελευταίο παράδειγμα, παραπάνω) μπορούμε να τη γράφουμε bab(a+b)*· και την παράσταση (((ab)+(a+b)*)(ba)*) (τελευταίο παράδειγμα) μπορούμε να τη γράφουμε (ab)+(a+b)*(ba)*.
Ορολογία: θα λέμε οτι μια Κ.Ε. παράγει το σύνολο των συμβολοσειρών που ανήκουν σ’ αυτήν.
![]() Άσκηση 2.5.1: Γράψτε
μερικές συμβολοσειρές που παράγονται από την κανονική έκφραση (a+aba)+.
Πώς θα περιγράφατε στα ελληνικά τις συμβολοσειρές του συνόλου αυτής της
κανονικής έκφρασης;
Άσκηση 2.5.1: Γράψτε
μερικές συμβολοσειρές που παράγονται από την κανονική έκφραση (a+aba)+.
Πώς θα περιγράφατε στα ελληνικά τις συμβολοσειρές του συνόλου αυτής της
κανονικής έκφρασης;
![]() Άσκηση 2.5.2: Γράψτε
την Κ.Ε. που παράγει τις συμβολοσειρές από το αλφάβητο {0,
1} που έχουν οποιαδήποτε ακολουθία από 0 ή 1 (της κενής ε
συμπεριλαμβανομένης), αλλά που δεν έχουν ποτέ δύο διαδοχικά 1.
Άσκηση 2.5.2: Γράψτε
την Κ.Ε. που παράγει τις συμβολοσειρές από το αλφάβητο {0,
1} που έχουν οποιαδήποτε ακολουθία από 0 ή 1 (της κενής ε
συμπεριλαμβανομένης), αλλά που δεν έχουν ποτέ δύο διαδοχικά 1.
![]() Άσκηση 2.5.3: Γράψτε
μια Κ.Ε. που παράγει όλες τις συμβολοσειρές που αποδέχεται
το ΜΠΑ-ε της
άσκησης 2.4.2.
Άσκηση 2.5.3: Γράψτε
μια Κ.Ε. που παράγει όλες τις συμβολοσειρές που αποδέχεται
το ΜΠΑ-ε της
άσκησης 2.4.2.
2.
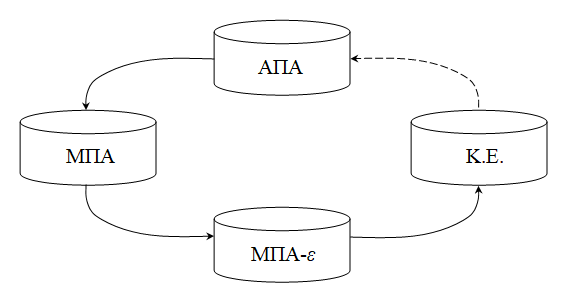
6 Ισοδυναμία κανονικών εκφράσεων και αυτομάτωνΣτη συνέχεια θα αποδείξουμε οτι οι τέσσερις μηχανισμοί που έχουμε ορίσει, δηλαδή (1) τα ΑΠΑ, (2) τα ΜΠΑ, (3) τα ΜΠα-ε, και (4) οι Κ.Ε., είναι ισοδύναμοι μεταξύ-τους.
Προς το σκοπό αυτόν πρώτα θα κάνουμε τη σύνδεση μεταξύ των Κ.Ε. και των ΜΠΑ-ε.
Θεώρημα 2.6.1: Για κάθε Κ.Ε. υπάρχει ένα ΜΠΑ-ε που απόδέχεται τη γλώσσα L που παράγει η Κ.Ε.
|
Απόδειξη. Χρησιμοποιώντας τον αναδρομικό ορισμό των Κ.Ε. θα κατασκευάσουμε το ΜΠΑ-ε που θα αποδέχεται τη γλώσσα που παράγει η Κ.Ε. Το αυτόματο αυτό θα έχει πάντα μία τελική κατάσταση χωρίς εξόδους (ακμές) από αυτήν. Η απόδειξη θα γίνει μέσω επαγωγής επί του εριθμού των τελεστών της Κ.Ε. Ας εξετάσουμε λοιπόν μία-μία τις περιπτώσεις του ορισμού της Κ.Ε. Οι πρώτες τρεις περιπτώσεις αποτελούν την επαγωγική βάση της απόδειξης. 1. Η Κ.Ε. είναι το κενό σύνολο (
2. Η. Κ.Ε. είναι το ε, δηλαδή η γλώσσα {ε}. Τότε το ΜΠΑ-ε που εικονίζεται στον παρακάτω γράφο προφανώς αποδέχεται επίσης την {ε}:
3. Η Κ.Ε. είναι το a, δηλαδή η γλώσσα {a}. Τότε το ΜΠΑ-ε που εικονίζεται στον παρακάτω γράφο προφανώς αποδέχεται επίσης την {a}:
4. Ερχόμαστε τώρα στο σημείο όπου θα
κάνουμε χρήση επαγωγής. Ας υποθέσουμε οτι το θεώρημα ισχύει για όλες τις
Κ.Ε. με λιγότερους από i τελεστές, όπου
i
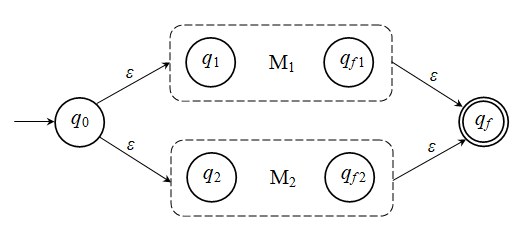
4α. Η Κ.Ε. r γράφεται ως r = r1 + r2. Εφόσον η r με τους i τελεστές-της έχει ως τελεστή το + (την ένωση), έπεται οτι καθεμία από τις r1 και r2 πρέπει να έχει λιγότερους από i τελεστές. Επομένως, εξ επαγωγής, υπάρχουν δύο ΜΠΑ-ε Μ1 = (Q1, Σ1, δ1, q1, {qf1}) και Μ2 = (Q2, Σ2, δ2, q2, {qf2}) που αποδέχονται, το μεν Μ1 τη γλώσσα που παράγει η r1, το δε Μ2 τη γλώσσα που παράγει η r2. Κατασκευάζουμε επομένως το Μ που εικονίζεται στον παρακάτω γράφο:
Δεν είναι καθόλου δύσκολο να ορίσουμε με ακρίβεια το ΜΠΑ-ε Μ που εικονίζεται παραπάνω. Συγκεκριμένα: Μ = (Q1
όπου η δ ορίζεται ως εξής:
Από την επαγωγική υπόθεση, οι καταστάσεις qf1 και qf2 δεν έχουν εξόδους (ακμές) στα Μ1 και Μ2 αντίστοιχα, επομένως όλες οι μεταβάσεις των Μ1 και Μ2 περιλαμβάνονται στο Μ. Βάσει των παραπάνω, δεν είναι καθόλου
δύσκολο να δούμε οτι υπάρχει μια
διαδρομή x
στο Μ από την
q0 στην qf
τότε και μονο τότε όταν: είτε υπάρχει μια διαδρομή
x στο Μ1
από την q1
στην qf1,
είτε υπάρχει μια διαδρομή x στο Μ2
από την q2
στην qf2.
Επομένως L(Μ) = L(Μ1)
4β. Η Κ.Ε. r γράφεται ως r = r1r2. Ορίζουμε τα Μ1 και Μ2 όπως στην περίπτωση 4α, και κατασκευάζουμε επομένως το Μ που εικονίζεται στον παρακάτω γράφο:
Τώρα το Μ ορίζεται ως εξής: Μ = (Q1
όπου η δ ορίζεται ως εξής:
Και πάλι είναι εύκολο να δούμε οτι
L(Μ) = {xy | x
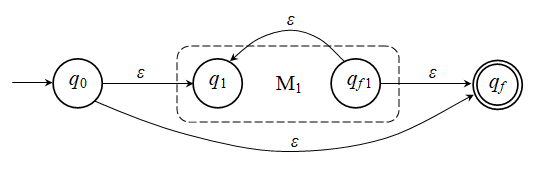
4γ. Η Κ.Ε. r γράφεται ως r = r1*. Έστω το Μ1 = (Q1, Σ1, δ1, q1, {qf1}), και L(Μ1) = r1. Κατασκευάζουμε το Μ που εικονίζεται στον εξής γράφο:
Ορίζουμε το Μ ως εξής: Μ = (Q1
όπου η δ ορίζεται ως εξής:
Έτσι, υπάρχει
μια διαδρομή x από την
q0
στην qf
στο Μ αν και μόνο αν μπορούμε να γράψουμε x =
x1x2
... xj
για κάποιο j
▓ |
![]() Άσκηση 2.6.1:
Κάνοντας χρήση της απόδειξης του θεωρήματος αυτού, κατασκευάστε ένα ΜΠΑ-ε
για την Κ.Ε.
(0
+ 01)*.
Μην απλοποιήσετε καμιά ακμή ή σύνολο καταστάσεων του προκύπτοντος
γράφου.
Άσκηση 2.6.1:
Κάνοντας χρήση της απόδειξης του θεωρήματος αυτού, κατασκευάστε ένα ΜΠΑ-ε
για την Κ.Ε.
(0
+ 01)*.
Μην απλοποιήσετε καμιά ακμή ή σύνολο καταστάσεων του προκύπτοντος
γράφου.
Ας ανακεφαλαιώσουμε τα συμπεράσματα που έχουμε συνάγει και αποδείξει έως τώρα.
Εικ. 2.6.1
Η παραπάνω εικόνα απεικονίζει τις σχέσεις μεταξύ των διαφόρων “μηχανών” (αυτομάτων και κανονικών εκφράσεων) που έχουμε βρει μέχρι τώρα. Το βέλος από το είδος μηχανής Χ στο είδος μηχανής Ψ πρέπει να ερμηνευτεί ως: «Χ → Ψ: δοσμένης μιας μηχανής τύπου Ψ, μπορούμε να κατασκευάσουμε μηχανή τύπου Χ που να αποδέχεται την ίδια γλώσσα όπως η Ψ.» Για παράδειγμα, το θεώρημα 2.6.1, παραπάνω, μας λέει οτι δοσμένης μιας μηχανής τύπου κανονικών εκφράσεων μπορούμε να κατασκευάσουμε μηχανή τύπου ΜΠΑ-ε που να αποδέχεται την ίδια γλώσσα.
Το βέλος από τις Κ.Ε. στα ΑΠΑ στην εικ. 2.6.1 σημειώνεται διακεκομμένο γιατί δεν έχουμε αποδείξει ακόμα οτι δοσμένου ενός ΑΠΑ μπορούμε να κατασκευάσουμε μια Κ.Ε. που να παράγει τη γλώσσα που αποδέχεται το ΑΠΑ· πράγμα που πρόκειται να αποδείξουμε ευθύς αμέσως.
Θεώρημα 2.6.2: Αν η γλώσσα L γίνεται αποδεκτή από ένα ΑΠΑ, τότε υπάρχει μια Κ.Ε. που παράγει την L.
|
Απόδειξη. Έστω οτι η L γίνεται αποδεκτή από το ΑΠΑ Μ με n καταστάσεις, που τις απαριθμούμε από το 1 ως το n: Μ = ({q1, ..., qn}, Σ, δ, q1, F)
πράγμα που ολοκληρώνει την επαγωγή. Για να ολοκληρώσουμε και την απόδειξη, πρέπει μόνο να παρατηρήσουμε οτι:
▓ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Με το παραπάνω θεώρημα, το διακεκομμένο βέλος της εικ. 2.6.1 μπορεί να μετατραπεί σε συνεχές.
Επειδή όμως δημιουργείται έτσι ένας κύκλος, έχουμε ουσιαστικά αποδείξει την ισοδυναμία των τεσσάρων αυτών ειδών μηχανών· γιατί, για να αποδείξουμε, για παράδειγμα, οτι κάθε Κ.Ε. μπορεί να παρασταθεί από ένα ΜΠΑ-ε, αρκεί να κάνουμε τον κύκλο, περνώντας από τις Κ.Ε. στα ΑΠΑ, στη συνέχεια στα ΜΠΑ, και τέλος στα ΜΠΑ-ε. Επομένως μπορούμε το όλο συμπέρασμα περί ισοδυναμίας να το παραστήσουμε με την εικόνα που ακολουθεί, όπου τα βέλη έχουν αντικατασταθεί από απλές ακμές ενός μη κατευθυνόμενου γράφου:
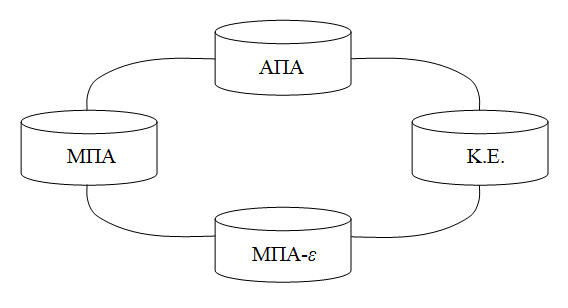
Εικ. 2.6.2
2.7 Άλλα είδη πεπερασμένων αυτομάτων
Τα ΑΠΑ, ΜΠΑ, ΜΠΑ-ε, και οι Κ.Ε. δεν είναι τα μόνα είδη αυτομάτων με υπολογιστικές δυνατότητες που είναι τελικά ισοδύναμες μεταξύ-τους. Υπάρχουν και άλλα είδη, όλα ισοδύναμα με τα παραπάνω. Μερικά από αυτά θα αναφερθούν με συντομία εδώ, χωρίς όμως αποδείξεις θεωρημάτων σχετικά με την ισοδυναμία-τους με τα ΑΠΑ, την οποία ο αναγνώστης θα πρέπει να θεωρήσει δεδομένη.
2.7.1 Πεπερασμένα αυτόματα διπλής κατεύθυνσης
Μέχρι τώρα, η συμβολοσειρά της εισόδου διαβαζόταν προς τη μία κατεύθυνση· ας πούμε, “από τα αριστερά προς τα δεξιά”, αν και αυτό εξαρτάται από το γεγονός οτι στην ελληνική (και σε άλλα “δυτικά” συστήματα γραφής) γράφουμε από τα αριστερά προς τα δεξιά. Η ουσιαστική παρατήρηση είναι οτι άπαξ και ένα σύμβολο εισόδου ιδωθεί από το αυτόματο και γίνει η επεξεργασία-του, το σύμβολο αυτό “χάνεται”, και το αυτόματο δεν ασχολείται πλέον με αυτό.
Είναι δυνατό να θεωρήσουμε αυτόματα “διπλής κατεύθυνσης”, όπου δηλαδή μια υποτιθέμενη “κεφαλή” που διαβάζει την είσοδο δεν κινείται μόνο προς μία κατεύθυνση (“από τα αριστερά προς τα δεξιά”), αλλά μπορεί να κινηθεί και προς την άλλη (“από τα δεξιά προς τα αριστερά”), ξαναδιαβάζοντας κάποια σύμβολα εισόδου που ήδη απασχόλησαν το αυτόματο. Έτσι, στην απεικόνιση δ, τις εντολές του τύπου «όντας στην κατάσταση qi και με σύμβολο εισόδου το a, πήγαινε στην κατάσταση qj» πρέπει να τις αντικαταστήσουμε με εντολές του τύπου: «όντας στην κατάσταση qi και με σύμβολο εισόδου το a, πήγαινε στην κατάσταση qj και μετακίνησε την κεφαλή ανάγνωσης της εισόδου κατά μία θέση [Αριστερά ή Δεξιά]». Δεν είναι καθόλου δύσκολο να κωδικοποιήσουμε με ένα μαθηματικό ορισμό αυτή την ιδέα:
Ορισμός: Ένα αιτιοκρατικό πεπερασμένο αυτόματο διπλής κατεύθυνσης (ΑΠΑ-2) είναι μια πεντάδα (Q, Σ, δ, q0, F), της οποίας όλα τα στοιχεία είναι όπως και στα ΑΠΑ, με εξαίρεση τη δ, η οποία τώρα είναι απεικόνιση από το Q X Σ στο Q X {Δ, Α}. Όταν δ(qi, a) = (qj, Δ), τότε το αυτόματο συμπεριφέρεται όπως και ένα απλό ΑΠΑ, δηλαδή: με σύμβολο το a στην είσοδο μεταφέρεται από την κατάσταση qi στην κατάσταση qj, και ετοιμάζεται να δεχτεί το επόμενο σύμβολο εισόδου (“Δεξιά”). Όταν όμως δ(qi, a) = (qj, Α), τότε το αυτόματο κάνει μεν το ίδιο ως προς το a και τις δύο καταστάσεις, αλλά αφού βρεθεί στην κατάσταση qj ετοιμάζεται να διαβάσει το σύμβολο που βρίσκεται πριν από το a στην είσοδο (“Αριστερά”). Αν δεν υπάρχει τέτοιο σύμβολο (που συμβαίνει στην αρχή της συμβολοσειράς εισόδου), τότε η δ εκεί δεν ορίζεται, και το αυτόματο απορρίπτει (δεν αποδέχεται) την είσοδο που του δόθηκε.
Το ΑΠΑ-2 αποδέχεται την είσοδό του αν βρεθεί σε τελική κατάσταση, και ταυτόχρονα έχει εξαντλήσει όλα τα σύμβολα εισόδου, δηλαδή η νοητή “κεφαλή” του ΑΠΑ-2 βρίσκεται “δεξιά” του τελευταίου συμβόλου εισόδου.

Εικ. 2.7.1: Σχηματική παράσταση “ταινίας εισόδου” και “κεφαλής” ενός ΑΠΑ-2.
Στην εικόνα 2.7.1 δίνεται μια σχηματική παράσταση εννοιών που δεν είναι απαραίτητες για τον ορισμό των ΑΠΑ-2, μας βοηθούν όμως στην κατανόηση των αυτομάτων, και καλό είναι να τις έχουμε υπόψη από εδώ και στο εξής. Θεωρούμε οτι η είσοδος είναι τοποθετημένη σε μια “ταινία”, την οποία “διαβάζει” το αυτόματο, ενώ υπάρχει και μια “κεφαλή” που μπορεί να μετακινηθεί αριστερά ή δεξιά στην ταινία. Η κεφαλή είναι τοποθετημένη πάντα μεταξύ των συμβόλων εισόδου, και στο επόμενο (χρονικά) “βήμα” διαβάζει και επεξεργάζεται (σύμφωνα με τη δ) το σύμβολο στα δεξιά-της, αν αυτό υπάρχει· διαβάζοντάς το όμως δεν μετακινείται παρά μόνο αν η δ της ορίσει να μετακινηθεί κατά μία θέση αριστερά ή δεξιά.
Καμία από τις παραπάνω έννοιες δεν χρειαζόταν να αναφερθεί στα άλλα αυτόματα που γνωρίσαμε μέχρι στιγμής, γιατί η “κεφαλή” μετακινείτο μόνο προς μία κατεύθυνση, και υποχρεωτικά μετά από την ανάγνωση του επόμενου συμβόλου εισόδου.
Άσκηση 2.7.1: Κατασκευάστε ένα ΑΠΑ-2 που να αποδέχεται τη γλώσσα που αποτελείται από συμβολοσειρές από το Σ = {a, b} με την εξής ιδιότητα: πριν από κάθε ακολουθία της μορφής bba υπάρχουν δέκα συνεχόμενα a. Σκεφτήτε τώρα πώς θα φτιάχνατε ένα απλό ΑΠΑ που να αποδέχεται την ίδια γλώσσα, και παρατηρήστε πώς το ΑΠΑ-2 απλοποιεί τη δομή αυτού του ΑΠΑ.
Μπορεί να αποδειχτεί οτι τα ΑΠΑ-2 αποδέχονται και αυτά τις κανονικές γλώσσες, επομένως είναι ισοδύναμα με τα άλλα τέσσερα μέλη της οικογένειας αυτομάτων που εξετάσαμε μέχρι στιγμής. Η απόδειξη είναι αρκετά περίπλοκη και υπερβαίνει το εύρος και τον σκοπό του παρόντος μαθήματος· ο αναγνώστης που ενδιαφέρεται γι’ αυτή μπορεί να συμβουλευτεί τη βιβλιογραφία στο [1]. Βεβαιωθήτε όμως οτι αντιλαμβάνεστε πώς ένα ΑΠΑ-2 μπορεί να προσομοιώσει ένα ΑΠΑ.
Επίσης, μπορούμε να ορίσουμε τα μη-αιτιοκρατικά αυτόματα διπλής κατεύθυνσης (ΜΠΑ-2), σε πλήρη αναλογία με τα ΜΠΑ και ΑΠΑ-2. Αποδεικνύεται οτι ούτε τα ΜΠΑ-2 προσθέτουν κάτι το καινούργιο, αλλά αποδέχονται κι αυτά τις κανονικές γλώσσες.
Επίσης, άλλη επέκταση στον ορισμό των αυτομάτων είναι να επιτρέπουμε στην “κεφαλή” να μην κινείται ούτε δεξιά ούτε αριστερά, αλλά να παραμένει ακίνητη δοσμένου ενός συμβόλου και όντας σε μια κατάσταση. Αποδεικνύεται οτι ούτε μ’ αυτή την προσθήκη επεκτείνουμε τις αποδεκτές γλώσσες πέρα από τις κανονικές.
2.7.2 Μηχανές Μουρ
Μια άλλη ιδέα που μπορούμε να προσθέσουμε στα μέχρι στιγμής αυτόματα είναι να παράγουν και κάποια σύμβολα εξόδου (κάτι ανάλογο με τον εκτυπωτή ενός υπολογιστή, ή με την οθόνη-του). Όλα τα αυτόματα που είδαμε μέχρι στιγμής απλώς διαβάζουν την είσοδό τους, και αν πρόκειται να απαντήσουν (να “εκτυπώσουν”) κάτι, αυτό είναι της μορφής: “απόρριψη” ή “αποδοχή”· δηλαδή είναι σαν να δίνουν σε μια “έξοδο” ένα μόνο δυαδικό ψηφίο πληροφορίας: το 0 ή το 1.
Η Μηχανή Μουρ (Moore) ορίζεται έτσι ώστε να μπορεί να συσχετίσει και ένα σύμβολο εξόδου με κάθε κατάστασή της, παρμένο από ένα αλφάβητο εξόδου. Συγκεκριμένα:
Ορισμός: Μια Μηχανή Μουρ είναι μια εξάδα (Q, Σ, Δ, δ, λ, q0), όπου τα Q, Σ, δ, και q0 είναι όπως και στα ΑΠΑ. Το Δ είναι ένα σύνολο συμβόλων που ονομάζεται αλφάβητο εξόδου. Και το λ είναι μια απεικόνιση από το Q στο Δ που συσχετίζει ένα σύμβολο εξόδου με κάθε κατάσταση.
Συνεπώς η
έξοδος μιας Μηχανής Μουρ δεδομένης μιας συμβολοσειράς
a1a2...an,
n
![]() 0, είναι η ακολουθία λ(q0)λ(q1)...λ(qn),
όπου q0,
q1,
..., qn
είναι η ακολουθία καταστάσεων έτσι ώστε δ(qi–1,
ai)
= qi
0, είναι η ακολουθία λ(q0)λ(q1)...λ(qn),
όπου q0,
q1,
..., qn
είναι η ακολουθία καταστάσεων έτσι ώστε δ(qi–1,
ai)
= qi
![]() 1
1
![]() i
i
![]() n.
n.
Προφανώς η Μηχανή Μουρ δίνει ως έξοδο το λ(q0) σαν απάντηση στο ε.
Βλέπουμε επίσης οτι η Μηχανή Μουρ δεν έχει τελική κατάσταση (ή καταστάσεις). Δεν χρειάζεται, γιατί τώρα η έννοια της αποδοχής ή απόρριψης έχει γενικευτεί, οπότε από το 0/1 έχει γίνει οποιαδήποτε συμβολοσειρά από το αλφάβητο εξόδου.
![]() Άσκηση 2.7.2: Δείξτε
με ποιον τρόπο οποιοδήποτε ΑΠΑ μπορεί να προσομοιωθεί από μια Μηχανή
Μουρ· δηλαδή, δοσμένου ενός ΑΠΑ, κατασκευάστε μια Μηχανή Μουρ που να κάνει ότι και το ΑΠΑ.
Άσκηση 2.7.2: Δείξτε
με ποιον τρόπο οποιοδήποτε ΑΠΑ μπορεί να προσομοιωθεί από μια Μηχανή
Μουρ· δηλαδή, δοσμένου ενός ΑΠΑ, κατασκευάστε μια Μηχανή Μουρ που να κάνει ότι και το ΑΠΑ.
2.7.3 Μηχανές Μήλυ
Αντί να παράγει σύμβολο εξόδου ανά κατάσταση, ένα αυτόματο θα μπορούσε να παράγει σύμβολο εξόδου ανά μετάβαση, δηλαδή ανά ακμή του γράφου-του. Αυτό ακριβώς κάνει μια Μηχανή Μήλυ (Mealy).
Ορισμός: Μια Μηχανή Μήλυ είναι μια εξάδα (Q, Σ, Δ, δ, λ, q0), όπου όλα τα στοιχεία-της είναι όπως στη Μηχανή Μουρ, εκτός από το λ, που τώρα απεικονίζει το Q X Σ στο Δ· ήτοι το λ(q, a) δίνει το σύμβολο εξόδου που αντιστοιχεί στη μετάβαση από την κατάσταση q δεδομένου του συμβόλου εισόδου a.
Συνεπώς η
έξοδος μιας Μηχανής Μήλυ δεδομένης μιας συμβολοσειράς
a1a2...an,
n
![]() 0, είναι η ακολουθία λ(q0,
a1)λ(q1,
a2)...λ(qn–1,
an),
όπου q0,
q1,
..., qn
είναι η ακολουθία καταστάσεων έτσι ώστε δ(qi–1,
ai)
= qi
0, είναι η ακολουθία λ(q0,
a1)λ(q1,
a2)...λ(qn–1,
an),
όπου q0,
q1,
..., qn
είναι η ακολουθία καταστάσεων έτσι ώστε δ(qi–1,
ai)
= qi
![]() 1
1
![]() i
i
![]() n. Η ακολουθία αυτή έχει μήκος
n, και όχι n
+ 1 όπως στη Μηχανή Μουρ.
n. Η ακολουθία αυτή έχει μήκος
n, και όχι n
+ 1 όπως στη Μηχανή Μουρ.
Προφανώς η Μηχανή Μήλυ δίνει ως έξοδο το ε σαν απάντηση στο ε.
![]() Άσκηση 2.7.3: Δείξτε
με ποιον τρόπο οποιαδήποτε Μηχανή Μουρ μπορεί να προσομοιωθεί από μια
Μηχανή Μήλυ· δηλαδή, δοσμένης μιας Μηχανής Μουρ, κατασκευάστε μια
Μηχανή Μήλυ που να κάνει ότι και η Μηχανή Μουρ.
Άσκηση 2.7.3: Δείξτε
με ποιον τρόπο οποιαδήποτε Μηχανή Μουρ μπορεί να προσομοιωθεί από μια
Μηχανή Μήλυ· δηλαδή, δοσμένης μιας Μηχανής Μουρ, κατασκευάστε μια
Μηχανή Μήλυ που να κάνει ότι και η Μηχανή Μουρ.
2.8 Ιδιότητες κλειστότητας κανονικών γλωσσών
Ένα χαρακτηριστικό των κανονικών γλωσσών είναι οτι υπάρχουν αλγόριθμοι για να απαντηθούν διάφορα ερωτήματα που τις αφορούν (πράγμα που θα δούμε οτι δεν ισχύει σε γλώσσες με μεγαλύτερες δυνατότητες). Για παράδειγμα: είναι η γλώσσα που παράγει ένα αυτόματο πεπερασμένη; Είναι κενή; Είναι το συμπλήρωμά της στο δοσμένο αλφάβητο κανονική γλώσσα; Αυτά και διάφορα άλλα ερωτήματα θα εξετάσουμε στη συνέχεια. Φυσικά, όταν βγάζουμε συμπεράσματα για κανονικές γλώσσες, ο αναγνώστης θα πρέπει να έχει κατά νου οτι τα ίδια συμπεράσματα βγάζουμε για όλα τα πεπερασμένα αυτόματα που έχουμε εξετάσει μέχρι στιγμής, εφόσον έχουμε αποδείξει (ή υποδείξει) την ισοδυναμία-τους.
Θεώρημα 2.8.1: Οι κανονικές γλώσσες είναι κλειστές ως προς την ένωση, τη συνένωση, και την κλειστότητα Κλέινι.
|
Απόδειξη. Προφανής λόγω του οτι κάθε κανονική γλώσσα παριστάνεται από μια Κ.Ε., και το αποτέλεσμα της ένωσης, συνένωσης, και κλειστότητας Κλέινι των Κ.Ε. είναι και πάλι Κ.Ε. ▓ |
Θυμίζουμε οτι κάθε γλώσσα είναι απλώς ένα σύνολο συμβολοσειρών από ένα αλφάβητο Σ. Επομένως το συμπλήρωμα L΄ μιας γλώσσας L είναι όλες οι συμβολοσειρές του Σ* – L.
Θεώρημα 2.8.2: Οι κανονικές γλώσσες είναι κλειστές ως προς την πράξη συμπλήρωμα.
|
Απόδειξη. Έστω η κανονική γλώσσα
L(Μ)
Για να κάνουμε αποδεκτό το σύνολο Σ*
– L, αρκεί να κατασκευάσουμε το ΑΠΑ Μ΄ =
(Q, Σ, δ, q0,
Q – F), δηλαδή να αντιστρέψουμε την ιδιότητα
“τελική” των καταστάσεων: όποιες δεν ήσαν τελικές στο Μ να γίνουν
τελικές στο Μ΄, και όποιες ήσαν τελικές στο Μ να μην είναι πλέον στο Μ΄.
Τότε το Μ΄ αποδέχεται τη συμβολοσειρά x
τότε και μόνο τότε όταν δ(q0,
x)
|
Το παραπάνω θεώρημα μας επιτρέπει να συμπεράνουμε την κλειστότητα για μια ακόμη πράξη συνόλων:
Θεώρημα 2.8.3: Οι κανονικές γλώσσες είναι κλειστές ως προς την πράξη της τομής.
|
Απόδειξη. Προκύπτει άμεσα από το γεγονός οτι
L1
|
2.9 Αποφασίσιμα προβλήματα
Στην προηγούμενη υποενότητα συναντήσαμε διάφορα προβλήματα για τα οποία υπάρχει μια πλήρης απάντηση. Για παράδειγμα, για το πρόβλημα: «Να κατασκευαστεί αυτόματο που να αποδέχεται το συμπλήρωμα μιας κανονικής γλώσσας», υπάρχει πλήρης απάντηση που δίνεται από την απόδειξη του θεωρήματος 2.8.2. Τα προβλήματα αυτά ονομάζονται αποφασίσιμα.
Ορισμός: Ένα πρόβλημα λέγεται αποφασίσιμο όταν υπάρχει αποτελεσματική μέθοδος η οποία δίνει λύση στο πρόβλημα αυτό.
Ορισμός: Μια μέθοδος για τη λύση ενός προβλήματος λέγεται αποτελεσματική όταν δίνει πάντοτε απάντηση (λύση) για οποιαδήποτε είσοδο δεδομένων του προβλήματος.
Παράδειγμα: Η εύρεση του μέγιστου κοινού διαιρέτη δύο ακεραίων είναι αποφασίσιμο πρόβλημα, γιατί υπάρχει αποτελεσματική μέθοδος που το λύνει: ο γνωστός “Ευκλείδειος αλγόριθμος”.
Στο παραπάνω παράδειγμα αναφέρθηκε η λέξη “αλγόριθμος” εντελώς περιστασιακά, χωρίς ορισμό. Αυτό δεν γίνεται χωρίς λόγο. Μέχρι σήμερα δεν υπάρχει πλήρης συμφωνία για το ποιες μέθοδοι πρέπει να ονομάζονται “αλγόριθμοι”. Εμείς θα ακολουθήσουμε την “κλασική” σχολή των Turing, Church, Kleene, και Gödel, σύμφωνα με την οποία ένας αλγόριθμος είναι οτιδήποτε μπορεί να εκτελεστεί από μια Μηχανή Τούρινγκ (Turing), μηχανή που θα γνωρίσουμε σε ένα από τα επόμενα κεφάλαια. Κατά την αντίληψη αυτή, ένας αλγόριθμος είναι κάτι παραπάνω (υπολογιστικά πιο ισχυρό) από μια αποτελεσματική μέθοδο.
Ορισμός: Τις αποτελεσματικές μεθόδους θα τις ονομάζουμε και πλήρεις αλγορίθμους.
Όρισμός: Μία μέθοδος που δίνει απαντήσεις σε ένα γνήσιο υποσύνολο όλων των δυνατών δεδομένων εισόδου-της, ενώ στα υπόλοιπα δεδομένα εισόδου δεν δίνει απάντηση (π.χ. συνεχίζει να υπολογίζει επ’ άπειρο) ονομάζεται ημιαποφασίσιμη, ή αλλιώς, ημιαλγόριθμος, και τα αντίστοιχα προβλήματα λέγονται ημιαποφασίσιμα.
Παράδειγμα: Το πρόβλημα της εύρεσης απόδειξης για οποιοδήποτε θεώρημα είναι ημιαποφασίσιμο. Υπάρχει δηλαδή ημιαλγόριθμος που έχει την εξής ιδιότητα: αν υπάρχει απόδειξη του θεωρήματος, δοσμένων των αξιωμάτων και των άλλων θεωρημάτων που έχουν ήδη αποδειχτεί, ο ημιαλγόριθμος αυτός θα βρει την απόδειξη και θα τη δώσει στην έξοδο· αν όμως δεν υπάρχει απόδειξη, τότε ο ημιαλγόριθμος θα συνεχίσει να δουλεύει επ’ άπειρο, ενώ ο παρατηρητής που περιμένει τη διαδικασία (το πρόγραμμα που υλοποιεί τον αλγόριθμο) να τελειώσει δεν γνωρίζει αν η διαδικασία θα τελειώσει κάποτε δίνοντας μια απόδειξη, ή αν θα συνεχίσει επ’ άπειρο. Αποδεικνύεται οτι δεν υπάρχει πλήρης αλγόριθμος που να λύνει το πρόβλημα της εύρεσης απόδειξης ενός θεωρήματος, αλλά μόνο ημιαλγόριθμος.
Θα αναβάλουμε τον ορισμό της έννοιας του γενικού αλγορίθμου μέχρι το κεφάλαιο των Μηχανών Τούρινγκ, όπου θα συναντήσουμε και τα αναποφασίσιμα προβλήματα, αυτά για τα οποία δεν υπάρχει αλγόριθμος που να τα λύνει.
Θεώρημα 2.9.1: Το πρόβλημα του αν η γλώσσα L που γίνεται αποδεκτή από το αυτόματο Μ είναι μη κενή, πεπερασμένη, ή άπειρη, είναι αποφασίσιμο.
Για να αποδείξουμε το θεώρημα 2.9.1 θα χρησιμοποιήσουμε δύο λήμματα, τα οποία και θα αποδείξουμε.
Λήμμα 2.9.1: Η γλώσσα L που γίνεται αποδεκτή από ένα αυτόματο Μ με n καταστάσεις είναι μη κενή τότε και μόνο τότε όταν το Μ αποδέχεται μια συμβολοσειρά μήκους l < n.
|
Απόδειξη. Αν το Μ αποδέχεται μια συμβολοσειρά μήκους l < n, τότε προφανώς η γλώσσα L είναι μη κενή. Έστω τώρα οτι η L(Μ)
είναι μη κενή· θα αποδείξουμε οτι το Μ αποδέχεται μια συμβολοσειρά
μήκους l < n.
Εφόσον η L(Μ) είναι μη κενή, έστω
x μια συμβολοσειρά της γλώσσας που είναι η
πιο σύντομη ή ίση σε μήκος με οποιαδήποτε
άλλη συμβολοσειρά της L(Μ). Αν |x|
|
Λήμμα 2.9.2: Η γλώσσα L
που γίνεται αποδεκτή από ένα αυτόματο Μ με n
καταστάσεις είναι άπειρη τότε και μόνο τότε όταν το Μ αποδέχεται μια
συμβολοσειρά μήκους l όπου
n
![]() l.
l.
|
Απόδειξη. Αν το Μ αποδέχεται μια συμβολοσειρά
μήκους l όπου n
|
Το θεώρημα 2.9.1 τώρα αποδεικνύεται με απλή χρήση των λημμάτων 2.9.1 και 2.9.2:
|
Απόδειξη του θεωρήματος 2.9.1. Κατασκευάζουμε το αυτόματο Μ΄ από το
Μ, ως εξής: στην απεικόνιση δ του Μ, σβήνουμε κάθε κατάσταση που δεν
μπορούμε να τη φτάσουμε από την αρχική κατάσταση του Μ με οποιαδήποτε
είσοδο. Κάθε κατάσταση και μετάβαση μεταξύ καταστάσεων που απομένει, την
προσθέτουμε στο Μ΄. Αν στο εναπομείναν σύνολο καταστάσεων του Μ΄ υπάρχει
τελική κατάσταση, τότε η L(Μ΄)
Επιπλέον τώρα, από το Μ' σβήνουμε κάθε
κατάσταση που δεν είναι τελική και από την οποία δεν μπορούμε να
φτάσουμε σε τελική κατάσταση. Από το λήμμα 2.9.2 έπεται οτι η
L(Μ΄)
Εφόσον μπορούμε να αποφασίσουμε αν η L(Μ) είναι κενή (ναι ή όχι), ή άπειρη (ναι ή όχι), έπεται οτι μπορούμε να αποφασίσουμε και αν είναι πεπερασμένη (ναι ή όχι). Συνεπώς το κάθε ένα από τα τρία προβλήματα είναι αποφασίσιμο. ▓ |
Παρατηρούμε οτι στην απόδειξη του θεωρήματος 2.9.1 έχουμε κατασκευές αυτομάτων, άρα αποτελεσματικές μεθόδους και πλήρεις αλγορίθμους που απαντούν τα ερωτήματα αυτά.
Θεώρημα 2.9.2: Το πρόβλημα του αν δύο αυτόματα Μ1 και Μ2 αποδέχονται την ίδια γλώσσα L είναι αποφασίσιμο.
|
Απόδειξη. Έστω L1
= L(Μ1), και
L2 =
L(Μ2).
Σχηματίζουμε τη γλώσσα
(L1
|
Θεώρημα 2.9.3: Δοσμένου ενός αυτομάτου Μ, υπάρχει ένα άλλο αυτόματο Μ΄ που αποδέχεται την ίδια γλώσσα όπως το Μ, και έχει μικρότερο ή ίσο αριθμό καταστάσεων από το Μ.
|
Το θεώρημα 2.9.3 θα το αφήσουμε χωρίς απόδειξη. Ο αναγνώστης που ενδιαφέρεται μπορεί να τη βρει στο [1]. |
Το παραπάνω θεώρημα μας λέει οτι μπορούμε πάντα να ελαχιστοποιήσουμε τον αριθμό των καταστάσεων ενός πεπερασμένου αυτομάτου.
3. Γραμματικές Χωρίς Συμφραζόμενα
3.1 Εισαγωγή στην έννοια της γραμματικής
Στην προηγούμενη ενότητα συναντήσαμε την έννοια του αυτομάτου. Στην παρούσα θα εξοικειωθούμε με την έννοια της γραμματικής. Αργότερα θα διαπιστώσουμε οτι υπάρχει πλήρης αντιστοιχία μεταξύ αυτομάτων και γραμματικών. Πάντως οι γραμματικές που θα εξετάσουμε στην παρούσα ενότητα θα είναι πιο ισχυρές σε υπολογιστική ικανότητα από τα αυτόματα που γνωρίσαμε. Ας δούμε όμως τί είναι μια γραμματική, μέσω ενός παραδείγματος από μια φυσική γλώσσα: την ελληνική.
Έστω οτι δίνονται οι παρακάτω κανόνες:
Πρόταση → ΟυσιαστικήΦράση ΡηματικήΦράση
ΟυσιαστικήΦράση → Άρθρο ΕπιθετικήΦράση
ΕπιθετικήΦράση → Επίθετο ΕπιθετικήΦράση
ΕπιθετικήΦράση → Ουσιαστικό
ΡηματικήΦράση → Ρήμα Επίρρημα
Άρθρο → το
Επίθετο → ανοιχτό
Επίθετο → μεγάλο
Ουσιαστικό → κουτί
Ουσιαστικό → παράθυρο
Ρήμα → έκλεισε
Ρήμα → χάλασε
Επίρρημα → εντελώς
Επίρρημα → θορυβωδώς
Κάθε κανόνας έχει ένα αριστερό και ένα δεξί μέλος, αριστερά και δεξιά του → αντιστοίχως. Όσες λέξεις αρχίζουν με κεφαλαίο γράμμα λέγονται “μεταβλητά σύμβολα”, ή απλώς “μεταβλητές”· ενώ όσες αρχίζουν με μικρό γράμμα λέγονται “τερματικά σύμβολα”, ή απλώς “τερματικά”. Κάθε μεταβλητή μπορεί να αντικατασταθεί μέσω ενός κανόνα που έχει αυτή τη μεταβλητή στο αριστερό-του μέλος, δηλαδή αριστερά από το →. Μας δίνεται επίσης η πληροφορία οτι η πρώτη από τις παραπάνω μεταβλητές (η “Πρόταση”) λέγεται “αρχική”.
Ξεκινάμε λοιπόν από την αρχική μεταβλητή:
(α) Πρόταση
Αυτή εμφανίζεται στον κανόνα 1:
1. Πρόταση → ΟυσιαστικήΦράση ΡηματικήΦράση
Αυτός ο κανόνας έχει δύο μεταβλητές: την ΟυσιαστικήΦράση και τη ΡηματικήΦράση, από τις οποίες μπορεί να αντικατασταθεί η Πρόταση. Επομένως η (α) γίνεται:
(β) ΟυσιαστικήΦράση ΡηματικήΦράση
Για την ΟυσιαστικήΦράση έχουμε τον κανόνα 2 όπου αυτή εμφανίζεται στο αριστερό μέλος:
2. ΟυσιαστικήΦράση → Άρθρο ΕπιθετικήΦράση
Αντκαθιστώντας μέσω αυτού του κανόνα την ΟυσιαστικήΦράση στη (β) παίρνουμε:
(γ) Άρθρο ΕπιθετικήΦράση ΡηματικήΦράση
Όσο για τη ΡηματικήΦράση, αυτή μπορούμε να την αντικαταστήσουμε μέσω του κανόνα 5:
5. ΡηματικήΦράση → Ρήμα Επίρρημα
Οπότε η (γ) γίνεται:
(δ) Άρθρο ΕπιθετικήΦράση Ρήμα Επίρρημα
Για το Άρθρο μας δίνεται μόνο μία επιλογή, μέσω του κανόνα 6, όπου το Άρθρο αντικαθίσταται από τερματικό σύμβολο:
(ε) το ΕπιθετικήΦράση Ρήμα Επίρρημα
Η ΕπιθετικήΦράση τώρα, αξίζει λίγο περισσότερη προσοχή, γιατί γι’ αυτήν έχουμε δύο κανόνες: τους 3 και 4, μέσω των οποίων μπορούμε να την αντικαταστήσουμε. Επιλέγουμε, αυθαίρετα, τον κανόνα 3:
3. ΕπιθετικήΦράση → Επίθετο ΕπιθετικήΦράση
οπότε η (ε) γίνεται:
(ϛ) το Επίθετο ΕπιθετικήΦράση Ρήμα Επίρρημα
Παραμένει δηλαδή η μεταβλητή ΕπιθετικήΦράση. Αν εφαρμόσουμε άλλη μια φορά τον κανόνα 3, παίρνουμε:
(ζ) το Επίθετο Επίθετο ΕπιθετικήΦράση Ρήμα Επίρρημα
Τώρα ας αντικαταστήσουμε την ΕπιθετικήΦράση μέσω του κανόνα 4:
4. ΕπιθετικήΦράση → Ουσιαστικό
Οπότε η (ζ) γίνεται:
(η) το Επίθετο Επίθετο Ουσιαστικό Ρήμα Επίρρημα
Τώρα έμειναν για αντικαταστάσεις μεταβλητών μόνο κανόνες που οδηγούν σε τερματικά σύμβολα. Αν κάνουμε ταυτόχρονη εφαρμογή των κανόνων 7, 8, 10, 11, 14 στην (η), παίρνουμε:
(θ) το ανοιχτό μεγάλο παράθυρο έκλεισε θορυβωδώς
η οποία είναι μια πιθανή πρόταση της ελληνικής γλώσσας.
Οι κανόνες αυτοί λέγονται συντακτικοί ή γραμματικοί κανόνες, και το σύστημα των 14 κανόνων συντακτικό ή γραμματική.
Στο παραπάνω παράδειγμα επιλέγαμε αυθαίρετα κανόνες προς εφαρμογή, με αποτέλεσμα να παραγάγουμε μια πρόταση (συμβολοσειρά, της οποίας όμως κάθε σύμβολο αντιστοιχεί σε ολόκληρη λέξη). Κάνοντας διαφορετική (αλλά πάντα αυθαίρετη) εφαρμογή κανόνων, θα μπορούσαμε να παραγάγουμε τις προτάσεις:
-
το παράθυρο χάλασε εντελώς
-
το μεγάλο ανοιχτό κουτί έκλεισε εντελώς
-
το μεγάλο μεγάλο μεγάλο ανοιχτό μεγάλο ανοιχτό κουτί χάλασε θορυβωδώς
Η τρίτη περίπτωση μας δείχνει οτι η γραμματική αυτή δημιουργεί και προτάσεις που δεν έχουν νόημα στην ελληνική γλώσσα. Λέμε όμως οτι είναι “συντακτικά σωστές”, εφόσον παρήχθησαν εφαρμόζοντας τους κανόνες από το δοσμένο σύνολο συντακτικών κανόνων.
Άσκηση 3.1.1: Τροποποιήστε τη γραμματική αυτή, περιορίζοντας και/ή αναδιατυπώνοντας τους κανόνες-της, ώστε να μην είναι δυνατό να παραχθούν απεριόριστα μεγάλες συμβολοσειρές όπως εκείνη της 3ης περίπτωσης, παραπάνω. Ποιος κανόνας είναι υπεύθυνος για τις απεριόριστες συμβολοσειρές;
Προς το παρόν, μέσω της παραπάνω γραμματικής δεν έχουμε πετύχει κάτι σπουδαίο, γιατί οι προτάσεις που παράγονται από τη γραμματική αυτή θα μπορούσαν να περιγραφούν επαρκώς και από μια Κανονική Έκφραση (Κ.Ε.).
![]() Άσκηση 3.1.2: Γράψτε
την Κ.Ε. που παράγει ακριβώς τις προτάσεις (συμβολοσειρές) που παράγει
και η ανωτέρω γραμματική.
Άσκηση 3.1.2: Γράψτε
την Κ.Ε. που παράγει ακριβώς τις προτάσεις (συμβολοσειρές) που παράγει
και η ανωτέρω γραμματική.
Τώρα όμως θα δούμε μια γραμματική η οποία παράγει προτάσεις (συμβολοσειρές) που είναι αδύνατο να παρασταθούν από οποιαδήποτε Κ.Ε. Πρόκειται για τη γραμματική των αριθμητικών εκφράσεων, ή έστω κάποιου υποσυνόλου αυτών:
Έκφραση → Όρος + Όρος | Όρος – Όρος | Όρος
Όρος → Παράγοντας * Παράγοντας | Παράγοντας / Παράγοντας | Παράγοντας
Παράγοντας → ( Έκφραση ) | Έκφραση
Έκφραση → Μεταβλητή | ΦυσικόςΑριθμός
Μεταβλητή → x | y | z
ΦυσικόςΑριθμός → Ψηφίο_0 | Ψηφίο19 Ψηφία
Ψηφία → Ψηφίο_0 Ψηφία | Ψηφίο19 Ψηφία | Ψηφίο_0 | Ψηφίο19
Ψηφίο19 → 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Ψηφίο_0 → 0
Αρχική μεταβλητή είναι η “Έκφραση”. Τα τερματικά σύμβολα σημειώνονται εδώ με κόκκινο χρώμα ώστε να ξεχωρίζουν από τα “συντακτικά σύμβολα” → και | . Πρέπει να παρατηρήσουμε εδώ οτι κάναμε χρήση του συμβόλου | (που το διαβάζουμε «είτε») ως συντομογραφία: Αντί να γράφουμε, π.χ.:
Α → α
Α → β
γράφουμε για συντομία:
Α → α | β
Κάτι άλλο που παρατηρούμε είναι οτι ένας κανόνας μπορεί να περιλαμβάνει μεταβλητές και τερματικά στο δεξί μέλος-του, σε οποιαδήποτε σειρά (σε αντίθεση με το πρώτο παράδειγμα όπου είχαμε διαχωρίσει μεταβλητές από τερματικά χάριν απλότητας).
Εύκολα βλέπουμε οτι η παραπάνω γραμματική, ξεκινώντας από την “Έκφραση”, παράγει συμβολοσειρές όπως οι ακόλουθες:
-
5 + 82
-
0 * x + (2 / 0)
-
((y – 1) / ((z) / 99))
-
(((((0)))))
Και πάλι, μέσω του παραπάνω παραδείγματος, βλέπουμε οτι άλλη έννοια είναι η “συντακτικά σωστή έκφραση”, και άλλη η “χρήσιμη έκφραση” (ή αλλιώς: “έκφραση που έχει νόημα”). Π.χ. η έκφραση (((((0))))) είναι μεν συντακτικά σωστή, εφόσον παράγεται από τη γραμματική του παραδείγματος, αλλά “δεν έχει νόημα”, αφού ποτέ δεν θα χρησιμοποιούσαμε μια τέτοια έκφραση στην πράξη.
Αυτό που διαθέτουν αυτές οι συμβολοσειρές, και που δεν μπορούμε να το παραγάγουμε μέσω Κ.Ε., είναι οτι έχουν πάντα “ζυγισμένες παρενθέσεις”· δηλαδή για κάθε αριστερή παρένθεση “(” υπάρχει μια δεξιά παρένθεση “)” που της αντιστοιχεί. Και αυτή η ικανότητα, το “ζύγισμα” των συμβόλων, όπως θα δούμε, είναι η ουσιαστική ικανότητα που διακρίνει τις “γραμματικές χωρίς συμφραζόμενα” (που θα ορίσουμε αμέσως) από όλα τα αυτόματα και τις Κ.Ε. που γνωρίσαμε μέχρι τώρα.
![]() Άσκηση 3.1.3:
Σκεφτήτε ένα παράδειγμα διαδοχικών φράσεων από την ελληνική γλώσσα (όχι
απαραίτητα πλήρων προτάσεων με ρήμα, χωρίς αυτό να απαγορεύεται) οι
οποίες να δείχνουν οτι το παραπάνω “ζύγισμα συμβόλων” υπάρχει και στη
φυσική γλώσσα. Όπως δηλαδή, μέσω του προηγούμενου παραδείγματος θα
παίρναμε διαδοχικές συμβολοσειρές όπως: (1), ((1)), (((1))), κλπ.,
σκεφτήτε ένα ανάλογο παράδειγμα και με φράσεις της ελληνικής — χωρίς να
δώσετε τη γραμματική με τους κανόνες-της, αλλά μόνο τις παραγόμενες
διαδοχικές φράσεις ή προτάσεις.
Άσκηση 3.1.3:
Σκεφτήτε ένα παράδειγμα διαδοχικών φράσεων από την ελληνική γλώσσα (όχι
απαραίτητα πλήρων προτάσεων με ρήμα, χωρίς αυτό να απαγορεύεται) οι
οποίες να δείχνουν οτι το παραπάνω “ζύγισμα συμβόλων” υπάρχει και στη
φυσική γλώσσα. Όπως δηλαδή, μέσω του προηγούμενου παραδείγματος θα
παίρναμε διαδοχικές συμβολοσειρές όπως: (1), ((1)), (((1))), κλπ.,
σκεφτήτε ένα ανάλογο παράδειγμα και με φράσεις της ελληνικής — χωρίς να
δώσετε τη γραμματική με τους κανόνες-της, αλλά μόνο τις παραγόμενες
διαδοχικές φράσεις ή προτάσεις.
Το “ζύγισμα” των συμβόλων είναι μια απαραίτητη ιδιότητα στο συντακτικό των γλωσσών προγραμματισμού. Π.χ. στις C, C++, και Java, οι εντολές προγράμματος κλείνονται μεταξύ ζευγών “{” και “}”· στην Pascal και σε απογόνους-της, κλείνονται μεταξύ ζευγών “begin” και “end”· στη Lisp και στους απογόνους-της, μεταξύ ζευγών “(” και “)”· κλπ.
3.2 Ορισμοί βασικών εννοιών
Ερχόμαστε τώρα στον ορισμό της έννοιας της γραμματικής χωρίς συμφραζόμενα.
Ορισμός:
Μια γραμματική χωρίς συμφραζόμενα (ΓΧΣ)
είναι μια τετράδα G = (V, T, P, S), όπου το
V είναι ένα πεπερασμένο σύνολο συμβόλων που θα
ονομάζουμε μεταβλητές, το
T είναι πεπερασμένο σύνολο συμβόλων που θα
ονομάζουμε τερματικά, το
P είναι ένα πεπερασμένο σύνολο
συντακτικών κανόνων, όπου κάθε
συντακτικός κανόνας είναι της μορφής Α → α, όπου το Α είναι
μεταβλητή, και το α είναι συμβολοσειρά από το (V
![]() T)*,
δηλαδή οποιαδήποτε ακολουθία (μπορεί και κενή) μεταβλητών ή τερματικών,
και τέλος το S
T)*,
δηλαδή οποιαδήποτε ακολουθία (μπορεί και κενή) μεταβλητών ή τερματικών,
και τέλος το S
![]() V είναι μία συγκεκριμένη μεταβλητή που ονομάζεται
αρχικό σύμβολο.
V είναι μία συγκεκριμένη μεταβλητή που ονομάζεται
αρχικό σύμβολο.
Τις γραμματικές αυτές τις λέμε “χωρίς συμφραζόμενα” γιατί οι κανόνες-τους είναι της μορφής Α → α, δηλαδή το αριστερό μέλος κάθε κανόνα είναι μια απλή μεταβλητή, “χωρίς συμφραζόμενα”. Σε επόμενη ενότητα του παρόντος μαθήματος θα γνωρίσουμε και γραμματικές με κανόνες της μορφής βΑγ → α, όπου τα β και γ είναι τα “συμφραζόμενα” του Α· δηλαδή για να εφαρμοστεί ο κανόνας αυτός θα πρέπει το Α να βρίσκεται “εντός των συμφραζομένων” β και γ. Καθώς δεν επιτρέπουμε τέτοιους κανόνες προς το παρόν, ονομάζουμε τις γραμματικές που δίνονται από τον προηγούμενο ορισμό “χωρίς συμφραζόμενα” (και για συντομία: “ΓΧΣ”).
Θα χρησιμοποιούμε τους συμβολισμούς των οποίων κάναμε χρήση και στην εισαγωγική παράγραφο· δηλαδή το σύμβολο | για τη σύμπτυξη κανόνων, κεφαλαία γράμματα για τις μεταβλητές, μικρά (πεζά) για τα τερματικά, κλπ.
Ορισμός: Αν
G = (V, T, P, S) είναι μια ΓΧΣ, το Α → α είναι ένας από
τους κανόνες του P, και τα β και γ
είναι συμβολοσειρές από το (V
![]() T)*,
τότε λέμε οτι ο κανόνας Α → α
εφαρμόζει στη συμβολοσειρά βΑγ και
παράγει το βαγ. Η
εφαρμογή του κανόνα Α → α θα λέγεται
παραγωγή (αγγλ.: derivation),
και θα συμβολίζεται έτσι: βΑγ
T)*,
τότε λέμε οτι ο κανόνας Α → α
εφαρμόζει στη συμβολοσειρά βΑγ και
παράγει το βαγ. Η
εφαρμογή του κανόνα Α → α θα λέγεται
παραγωγή (αγγλ.: derivation),
και θα συμβολίζεται έτσι: βΑγ
![]() βαγ.
Το συμβολισμό αυτό θα τον διαβάζουμε ως εξής: «το βΑγ
παράγει απευθείας το βαγ.»
(Θα δούμε αμέσως τί σημαίνει να παράγεται κάποια συμβολοσειρά αλλά όχι
απευθείας.)
βαγ.
Το συμβολισμό αυτό θα τον διαβάζουμε ως εξής: «το βΑγ
παράγει απευθείας το βαγ.»
(Θα δούμε αμέσως τί σημαίνει να παράγεται κάποια συμβολοσειρά αλλά όχι
απευθείας.)
Έτσι, σε μια γραμματική
G, δύο συμβολοσειρές σχετίζονται με τη σχέση
![]() όταν η μία
παράγει απευθείας την άλλη.
όταν η μία
παράγει απευθείας την άλλη.
Ορισμός: Έστω και πάλι η
G όπως και προηγουμένως. Ας υποθέσουμε τώρα
οτι τα α1,
α2, ...
, αn
είναι συμβολοσειρές από το (V
![]() T)*,
όπου n
T)*,
όπου n
![]() 1, και οτι:
1, και οτι:
α1
![]() α2
α2
![]() ...
αn–1
...
αn–1
![]() αn.
αn.
Τότε λέμε οτι το α1
παράγει το
αn
στη γραμματική G (όχι κατανάγκη απευθείας,
όπως στον προηγούμενο ορισμό). Την παραγωγή αυτή θα τη συμβολίζουμε
έτσι: α1
![]() αn.
αn.
Με άλλα λόγια, μπορούμε να πούμε οτι η
σχέση ![]() είναι η ανακλαστική και μεταβατική
κλειστότητα της σχέσης
είναι η ανακλαστική και μεταβατική
κλειστότητα της σχέσης
![]() .
Εναλλακτικά, α
.
Εναλλακτικά, α
![]() β
τότε και μόνο τότε αν το β παράγεται από το α μέσω μηδέν ή
περισσότερων παραγωγών του συνολου P της
G.
β
τότε και μόνο τότε αν το β παράγεται από το α μέσω μηδέν ή
περισσότερων παραγωγών του συνολου P της
G.
Ορισμός: Η
γλώσσα L(G) που παράγεται
από τη γραμματική G = (V, T, P, S) είναι το
σύνολο {w | w
![]() T* και
S
T* και
S
![]() w}.
w}.
Με άλλα λόγια, μια συμβολοσειρά ανήκει στην L(G) αν:
-
η συμβολοσειρά αποτελείται αποκλειστικά από τερματικά σύμβολα, και
-
η συμβολοσειρά μπορεί να παραχθεί από το S.
Ορισμός: γλώσσα χωρίς συμφραζόμενα ονομάζεται η γλώσσα L(G) που παράγεται από μια G που είναι ΓΧΣ.
Παράδειγμα: Έστω η G = (V, T, P, S), όπου V = {S, A, B}, T = {0, 1}, και το P είναι το εξής σύνολο κανόνων:
-
S → 0Β | 1Α
-
Α → 0 | 0S | 1ΑΑ
-
Β → 1 | 1S | 0ΒΒ
Μπορεί να αποδειχτεί, μέσω επαγωγής στο μήκος της παραγόμενης συμβολοσειράς, οτι η γλώσσα χωρίς συμφραζόμενα L(G) είναι το σύνολο όλων των συμβολοσειρών στο Τ+ που αποτελούνται από ίσο αριθμό από 0 και 1.
![]() Άσκηση 3.2.1:
(Α) Διατυπώστε κανόνες για μια ΓΧΣ που παράγει όλες τις συμβολοσειρές
από το αλφάβητο Τ={α, β} της μορφής αnβn,
όπου n
Άσκηση 3.2.1:
(Α) Διατυπώστε κανόνες για μια ΓΧΣ που παράγει όλες τις συμβολοσειρές
από το αλφάβητο Τ={α, β} της μορφής αnβn,
όπου n
![]() 1, και μόνο αυτές. (Β) Πώς πρέπει να τροποποιηθούν οι κανόνες ώστε να
περιλάβουν και την περίπτωση n = 0;
1, και μόνο αυτές. (Β) Πώς πρέπει να τροποποιηθούν οι κανόνες ώστε να
περιλάβουν και την περίπτωση n = 0;
Σημείωση: από εδώ και στο εξής, σε παρόμοιες ασκήσεις, το «και μόνο αυτές» θα το παραλείπουμε ως εννοούμενο.
![]() Άσκηση 3.2.2:
Διατυπώστε κανόνες για μια ΓΧΣ που παράγει όλες τις συμβολοσειρές από
το αλφάβητο Τ={α, β} της μορφής αnβn+1,
όπου n
Άσκηση 3.2.2:
Διατυπώστε κανόνες για μια ΓΧΣ που παράγει όλες τις συμβολοσειρές από
το αλφάβητο Τ={α, β} της μορφής αnβn+1,
όπου n
![]() 1.
1.
![]() Άσκηση 3.2.3:
Διατυπώστε κανόνες για μια ΓΧΣ που παράγει όλες τις συμβολοσειρές από
το αλφάβητο Τ={α, β} της μορφής αnβm,
όπου n
> m, και n,
m
Άσκηση 3.2.3:
Διατυπώστε κανόνες για μια ΓΧΣ που παράγει όλες τις συμβολοσειρές από
το αλφάβητο Τ={α, β} της μορφής αnβm,
όπου n
> m, και n,
m
![]() 1
1
![]() Άσκηση 3.2.4:
Διατυπώστε κανόνες για μια ΓΧΣ που παράγει όλες τις συμβολοσειρές
από το αλφάβητο Τ={α, β} οι οποίες είναι
παλίνδρομα. (Θυμίζουμε οτι η κενή
συμβολοσειρά είναι κι αυτή παλίνδρομο.)
Άσκηση 3.2.4:
Διατυπώστε κανόνες για μια ΓΧΣ που παράγει όλες τις συμβολοσειρές
από το αλφάβητο Τ={α, β} οι οποίες είναι
παλίνδρομα. (Θυμίζουμε οτι η κενή
συμβολοσειρά είναι κι αυτή παλίνδρομο.)
![]() Άσκηση 3.2.5:
Έχοντας λύσει την προηγούμενη άσκηση (3.2.4), διατυπώστε κανόνες για μια
ΓΧΣ που παράγει όλες τις συμβολοσειρές από το αλφάβητο Τ={α, β} οι
οποίες έχουν άρτιο μήκος (μπορεί και 0), και αν χωριστούν στη μέση τότε
τα α και β στα δύο μισά αποτελούν “αντικατοπτρισμό” το ένα του άλλου
(όπως π.χ. στα ααβ·αββ, αβαββββα·βααααβαβ, κλπ, όπου με · σημειώσαμε το
μέσον, χωρίς αυτό το σύμβολο να ανήκει στη συμβολοσειρά).
Άσκηση 3.2.5:
Έχοντας λύσει την προηγούμενη άσκηση (3.2.4), διατυπώστε κανόνες για μια
ΓΧΣ που παράγει όλες τις συμβολοσειρές από το αλφάβητο Τ={α, β} οι
οποίες έχουν άρτιο μήκος (μπορεί και 0), και αν χωριστούν στη μέση τότε
τα α και β στα δύο μισά αποτελούν “αντικατοπτρισμό” το ένα του άλλου
(όπως π.χ. στα ααβ·αββ, αβαββββα·βααααβαβ, κλπ, όπου με · σημειώσαμε το
μέσον, χωρίς αυτό το σύμβολο να ανήκει στη συμβολοσειρά).
3.3 Παραγωγικά δέντρα
Συνδεόμενη με την έννοια της παραγωγής σε μια γραμματική είναι η έννοια του παραγωγικού δέντρου. Ας θεωρήσουμε και πάλι το παράδειγμα της γραμματικής των αριθμητικών εκφράσεων, που έχει τους κανόνες:
Έκφραση → Όρος + Όρος | Όρος – Όρος | Όρος
Όρος → Παράγοντας * Παράγοντας | Παράγοντας / Παράγοντας | Παράγοντας
Παράγοντας → ( Έκφραση ) | Έκφραση
Έκφραση → Μεταβλητή | ΦυσικόςΑριθμός
Μεταβλητή → x | y | z
ΦυσικόςΑριθμός → Ψηφίο_0 | Ψηφίο19 Ψηφία
Ψηφία → Ψηφίο_0 Ψηφία | Ψηφίο19 Ψηφία | Ψηφίο_0 | Ψηφίο19
Ψηφίο19 → 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Ψηφίο_0 → 0
Οπως είδαμε, η συμβολοσειρά 0 * x + (2 / 0) παράγεται από τη γραμματική αυτή, δηλαδή:
Έκφραση
![]() 0 * x
+ (2 / 0)
0 * x
+ (2 / 0)
Αυτή όμως η παράσταση της παραγωγής δεν μας δίνει την πλήρη πληροφορία του πώς παρήχθη τελικά η συμβολοσειρά, δηλαδή μέσω ποιων βημάτων (αντικαταστάσεων μεταβλητών μέσω κανόνων). Θα μπορούσαμε να γράψουμε:
Έκφραση
![]() Όρος
Όρος
![]() Παράγοντας
* Παράγοντας
Παράγοντας
* Παράγοντας
![]() ...
...
![]() 0 * x
+ (2 / 0)
0 * x
+ (2 / 0)
με μια μακριά αλυσίδα παραγωγών. Ένας όμως πιο παραστατικός τρόπος της πλήρους παραγωγής δίνεται μέσω του ακόλουθου δέντρου:
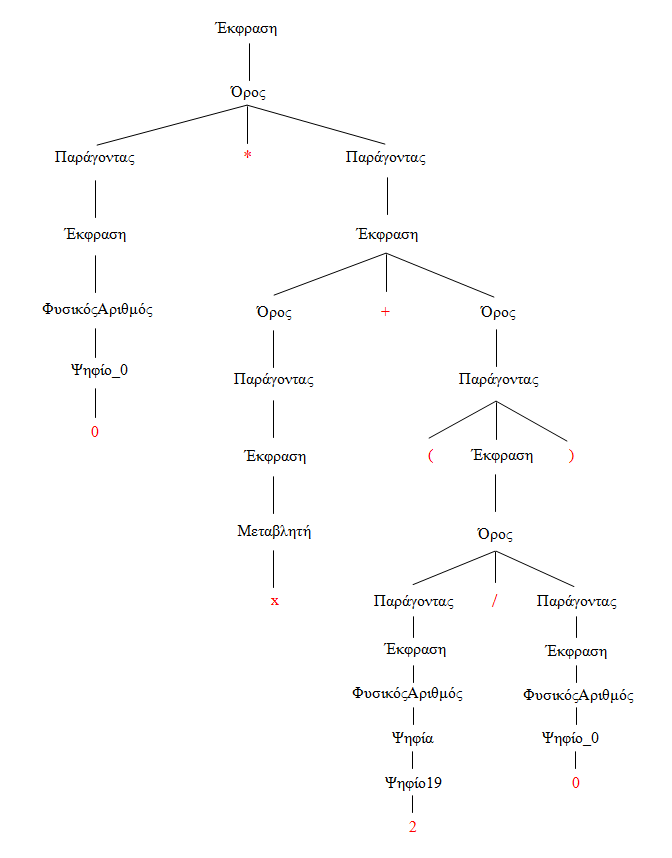
Εικ. 3.3.1: Παραγωγικό δέντρο για την έκφραση 0 * x + (2 / 0)
Το δεντρο αυτό λέγεται παραγωγικό δέντρο (αγγλ.: parse tree, ή derivation tree). Πιο συγκεκριμένα:
Ορισμός: Έστω G = (V, T, P, S) μια ΓΧΣ Ένα δέντρο ονομάζεται παραγωγικό δέντρο για τη G αν:
-
Σε κάθε κορυφή αντιστοιχεί μια ετικέτα, δηλαδή ένα σύμβολο από το V
 T
T
 { ε }.
{ ε }. -
Η ετικέτα της ρίζας είναι το S.
-
Αν μια κορυφή είναι εσωτερική (όχι φύλλο του δέντρου) και έχει ετικέτα το Α, τότε πρέπει Α
 V.
V. -
Αν η κορυφή n έχει ετικέτα Α, και είναι γονέας των τέκνων n1, n2, ... nk, με αυτή τη διάταξη από αριστερά προς τα δεξιά, με ετικέτες Χ1, Χ2, ... Χk αντίστοιχα, τότε το Α → Χ1Χ2...Χk πρέπει να είναι ένας κανόνας του P.
-
Αν η κορυφή n έχει ετικέτα ε, τότε το n πρέπει να είναι φύλλο και μοναδικό τέκνο του γονέα-του.
Άσκηση 3.3.2: Κατασκευάστε το παραγωγικό δέντρο για την παραγωγή της συμβολοσειράς 0011 μέσω της γραμματικής που διατυπώσατε στη λύση της άσκησης 3.2.1.
Ορισμός: Ένα υποδέντρο (αγγλ.: subtree) ενός παραγωγικού δέντρου είναι μία κορυφή του παραγωγικού δέντρου μαζί με όλους τους απογόνους-της, δηλαδή όλες τις κορυφές (είτε εσωτερικές είτε φύλλα) για τις οποίες υπάρχουν διαδρομές προς αυτές από την κορυφή. Αν η ετικέτα της ρίζας του υποδέντρου είναι το Α, τότε στο υποδέντρο αυτό αναφερόμαστε ως Α-δέντρο.
Συνεπώς, “S-δέντρο” είναι ένας εναλλακτικός τρόπος να αναφερθούμε στο συνολικό παραγωγικό δέντρο.
Ορισμός: Έστω ένα υποδέντρο μιας ΓΧΣ. Το προϊόν (αγγλ.: yield) του υποδέντρου είναι η συμβολοσειρά που προκύπτει αν επισκεφθούμε τις κορυφές του υποδέντρου αναδρομικά και με κατά βάθος προτεραιότητα (αγγλ.: depth-first), από αριστερά προς τα δεξιά, και παραθέσουμε τα τερματικά σύμβολα που συναντάμε κατά την επίσκεψη αυτή.
Παράδειγμα: η συμβολοσειρά 0 * x + (2 / 0) είναι το προϊόν του παραγωγικού δέντρου του αρχικού παραδείγματος αυτής της υποενότητας.
Ισχύει επίσης το εξής:
Θεώρημα 3.3.1: Έστω G = (V, T, P, S)
μια ΓΧΣ. Τότε S
![]() α
αν και μόνο αν υπάρχει παραγωγικό υποδέντρο στην G
με προϊόν το α.
α
αν και μόνο αν υπάρχει παραγωγικό υποδέντρο στην G
με προϊόν το α.
Η απόδειξη του παραπάνω θεωρήματος είναι εκτός του εύρους του παρόντος μαθήματος.
Ορισμός: Αν σε καθε βήμα της παραγωγής ενός προϊόντος επιλέγεται προς αντικατάσταση μέσω ενός κανόνα-της η πιο αριστερά ευρισκόμενη μεταβλητή, τότε η παραγωγή αυτή λέγεται αριστερή παραγωγή. Αντίστοιχα, αν επιλέγεται πάντα η πιο δεξιά ευρισκόμενη μεταβλητή, τότε η παραγωγή λέγεται δεξιά παραγωγή.
Παράδειγμα: Έστω η ΓΧΣ. G = (V, T, P, S) με V = {S, A, B}, T = {α, β}, και P το εξής:
-
S → αΑ | αΒ
-
Α → α | ΑΒ
-
Β → β | αβ
Τότε η συμβολοσειρά ααβ έχει την εξής αριστερή παραγωγή:
S
![]() αΑ
αΑ
![]() αΑΒ
αΑΒ
![]() ααΒ
ααΒ
![]() ααβ
ααβ
Έχει όμως και την ακόλουθη δεξιά παραγωγή:
S
![]() αΑ
αΑ
![]() αΑΒ
αΑΒ
![]() αΑβ
αΑβ
![]() ααβ
ααβ
Όπως βλέπουμε, στο τρίτο βήμα παραγωγής, από τη συμβολοσειρά αΑΒ επιλέγεται προς αντικατάσταση το Α όταν έχουμε αριστερή παραγωγή, ενώ το Β όταν έχουμε δεξιά παραγωγή.
Στο παραπάνω παράδειγμα συμβαίνει και κάτι άλλο: η συμβολοσειρά ααβ έχει δύο διαφορετικές παραγωγές (και αντίστοιχα παραγωγικά δέντρα):
-
S
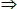 αΑ
αΑ
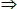 αΑΒ
αΑΒ
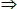 ααΒ
ααΒ
 ααβ
ααβ -
S
 αΒ
αΒ
 ααβ
ααβ
Ορισμός: Μια ΓΧΣ G της οποίας κάποιο προϊόν έχει δύο διαφορετικά παραγωγικά δέντρα ονομάζεται διφορούμενη (ή ασαφής, ή αμφίσημη· αγγλ.: ambiguous).
Παράδειγμα: Η ΓΧΣ του προηγούμενου παραδείγματος είναι προφανώς διφορούμενη, αφού η συμβολοσειρά ααβ, όπως είδαμε, έχει δύο διαφορετικά παραγωγικά δέντρα.
Ορισμός: Μια γλώσσα χωρίς συμφραζόμενα της οποίας κάθε ΓΧΣ είναι διφορούμενη, ονομάζεται εγγενώς διφορούμενη γλώσσα.
Παράδειγμα: Μπορεί να αποδειχθεί (αν και η απόδειξη είναι αρκετά περίπλοκη) οτι η γλώσσα:
L = { αnβnγmδm
| n
![]() 1, m
1, m
![]() 1 }
1 }
![]() { αnβmγmδn
| n
{ αnβmγmδn
| n
![]() 1, m
1, m
![]() 1 }
1 }
είναι εγγενώς διφορούμενη.
Η έννοια της εγγενώς διφορούμενης γλώσσας είναι πολύ σημαντική στις γλώσσες προγραμματισμού, όπου, για λόγους αποδοτικότητας (ταχύτητας) των μεταγλωττιστών, αποφεύγουμε μια γλώσσα προγραμματισμού να είναι εγγενώς διφορούμενη. Πρακτικά όλες οι γνωστές γλώσσες προγραμματισμού είναι μη διφορούμενες.
3.4 Απλοποιήσεις σε ΓΧΣ
Οι κανόνες των ΓΧΣ είναι δυνατό να απλοποιηθούν σημαντικά μέσω διάφορων αυτοματοποιημένων μεθόδων (αλγορίθμων). Μια γραμματική μπορεί να περιλαμβάνει άχρηστα σύμβολα, κενούς κανόνες, και/ή μοναδιαίους κανόνες. Ας δούμε, μία-μία, αυτές τις περιπτώσεις.
3.4.1 Άχρηστα σύμβολα
Ορισμός: Έστω G = (V, T, P, S)
μια ΓΧΣ. Ένα σύμβολο Χ
![]() V
V
![]() T
ονομάζεται χρήσιμο αν υπάρχει
παραγωγή της μορφής S
T
ονομάζεται χρήσιμο αν υπάρχει
παραγωγή της μορφής S
![]() aXb
aXb
![]() w,
όπου a, b
w,
όπου a, b
![]() (V
(V
![]() T)*
και w
T)*
και w
![]() T*. Αλλιώς το
Χ ονομάζεται άχρηστο.
T*. Αλλιώς το
Χ ονομάζεται άχρηστο.
Σύμφωνα με τον παραπάνω ορισμό, για να
είναι το Χ χρήσιμο, πρέπει να συμβαίνουν δύο πράγματα: πρώτο, πρέπει το
Χ να μπορεί να παραγάγει κάποια συμβολοσειρά αποτελούμενη από τερματικά
σύμβολα (X
![]() w)·
και δεύτερο, το Χ πρέπει να εμφανίζεται σε μια συμβολοσειρά που
παράγεται από το S (S
w)·
και δεύτερο, το Χ πρέπει να εμφανίζεται σε μια συμβολοσειρά που
παράγεται από το S (S
![]() aXb). Ας δούμε έναν αλγόριθμο μέσω του οποίου
βρίσκουμε όλα τα Χ τέτοια ώστε X
aXb). Ας δούμε έναν αλγόριθμο μέσω του οποίου
βρίσκουμε όλα τα Χ τέτοια ώστε X
![]() w
για κάποιο w
w
για κάποιο w
![]() T*.
T*.
έστω σύνολο ΠαλαιόV ←
έστω σύνολο ΝέοV ← { Α | Α → w για κάποιο w
T* }
όσο ΠαλαιόV
ΝέοV επανάλαβε:
ΠαλαιόV ← ΝέοV
ΝέοV ← ΠαλαιόV
{ Α | Α → a για κάποιο a
(Τ
ΠαλαιόV)* }
Το νέο σύνολο μεταβλητών είναι το ΝέοV.
Ας κάνουμε μια εφαρμογή του παραπάνω αλγορίθμου. Έστω η ΓΧΣ G = (V, T, P, S) με το εξής σύνολο κανόνων Ρ:
-
S → Αα | ΑΒ
-
Α → αC | β
-
Β → ΒΑ
-
C → Αα
Ξεκινάμε τον αλγόριθμο με τα σύνολα
ΠαλαιόV ίσο με
![]() , και
ΝέοV = { Α }, λόγω του κανόνα Α → β, εφόσον β
, και
ΝέοV = { Α }, λόγω του κανόνα Α → β, εφόσον β
![]() T.
T.
Μπαίνοντας στην ανακύκλωση του
αλγορίθμου (εφόσον ΠαλαιόV
![]() ΝέοV),
θέτουμε ΠαλαιόV ← { Α }, και στο αμέσως
επόμενο βήμα, ΝέοV ← { Α }
ΝέοV),
θέτουμε ΠαλαιόV ← { Α }, και στο αμέσως
επόμενο βήμα, ΝέοV ← { Α }
![]() {
C }, εφόσον υπάρχει ο κανόνας
C → Αα, και Αα
{
C }, εφόσον υπάρχει ο κανόνας
C → Αα, και Αα
![]() (Τ
(Τ
![]() { Α
})*. Άρα τώρα ΝέοV
είναι το { Α, C }.
{ Α
})*. Άρα τώρα ΝέοV
είναι το { Α, C }.
Συνεχίζουμε στην ανακύκλωση γιατί
ΠαλαιόV
![]() ΝέοV.
Θέτουμε ΠαλαιόV ← { Α, C
}. Τώρα όμως δεν μπορούμε να βρούμε άλλον κανόνα ώστε να επεκτείνουμε το
ΝέοV. Έτσι ΠαλαιόV =
ΝέοV, οπότε βγαίνουμε από την ανακύκλωση, και
το νέο σύνολο μεταβλητών είναι το { Α, C }.
Επομένως απαλλαχθήκαμε από τη μεταβλητή Β.
ΝέοV.
Θέτουμε ΠαλαιόV ← { Α, C
}. Τώρα όμως δεν μπορούμε να βρούμε άλλον κανόνα ώστε να επεκτείνουμε το
ΝέοV. Έτσι ΠαλαιόV =
ΝέοV, οπότε βγαίνουμε από την ανακύκλωση, και
το νέο σύνολο μεταβλητών είναι το { Α, C }.
Επομένως απαλλαχθήκαμε από τη μεταβλητή Β.
Με ένα δεύτερο, πολύ απλό αλγόριθμο,
δοσμένης μιας ΓΧΣ G = (V, T, P, S), μπορούμε
να βρούμε μια ισοδύναμη ΓΧΣ G΄ = (V΄, T΄, P΄, S)
τέτοια ώστε για κάθε Χ
![]() (V΄
(V΄![]() T΄)
να υπάρχουν a και b
T΄)
να υπάρχουν a και b
![]() (V΄
(V΄![]() T΄)*
για τα οποία να ισχύει S
T΄)*
για τα οποία να ισχύει S
![]() aΧb. Οπότε θα ικανοποιηθεί και η
δεύτερη συνθήκη περί χρήσιμων συμβόλων. Ο αλγόριθμος αυτός είναι ο εξής:
aΧb. Οπότε θα ικανοποιηθεί και η
δεύτερη συνθήκη περί χρήσιμων συμβόλων. Ο αλγόριθμος αυτός είναι ο εξής:
έστω σύνολα V΄ ← { S } και Τ΄ ←
για κάθε Α
V΄ που δεν έχει εξεταστεί ακόμη, και με κανόνα Α → w επανάλαβε:
βάλε όλες τις μεταβλητές του w στο V΄
βάλε όλα τα τερματικά του w στο Τ΄
Το Ρ΄ είναι το σύνολο των κανόνων του Ρ που περιέχουν μόνο σύμβολα από το V΄
T΄.
Ας παρατηρήσουμε οτι οι παραπάνω δύο αλγόριθμοι πρέπει να εφαρμοστούν με τη σειρά που αναφέρθηκαν (βλ. άσκηση 3.4.2).
Με εφαρμογή τόσο του 1ου όσο και του 2ου αλγορίθμου, το σύμβολο Β κρίνεται άχρηστο, και ο κανόνας Β → ΒΑ δεν περιλαμβάνεται στην τελική γραμματική.
![]() Άσκηση 3.4.1: Έστω η
γραμματική με κανόνες:
Άσκηση 3.4.1: Έστω η
γραμματική με κανόνες:
-
S → ΑΒ | α
-
Α → α
Εφαρμόστε τους δύο παραπάνω αλγορίθμους για να την απαλλάξετε από άχρηστα σύμβολα και κανόνες.
![]() Άσκηση 3.4.2: Τί θα
συμβεί στην προηγούμενη άσκηση αν εφαρμόσουμε πρώτα το 2ο αλγόριθμο, και
μετά τον 1ο;
Άσκηση 3.4.2: Τί θα
συμβεί στην προηγούμενη άσκηση αν εφαρμόσουμε πρώτα το 2ο αλγόριθμο, και
μετά τον 1ο;
3.4.2 Κενοί κανόνες
Αν η L(G) μιας ΓΧΣ G περιλαμβάνει την κενή συμβολοσειρά ε, ασφαλώς δεν μπορούμε να απαλείψουμε όλους τους κανόνες της μορφής Α → ε. Αν όμως το ε δεν περιλαμβάνεται στην L(G), τότε μπορούμε να απαλείψουμε κάθε τέτοιον κενό κανόνα.
Ορισμός: Έστω G = (V, T, P, S)
μια ΓΧΣ. Μια μεταβλητή Α
![]() V ονομάζεται
μηδενίσιμη αν Α
V ονομάζεται
μηδενίσιμη αν Α
![]() ε.
ε.
Προκειμένου να απαλείψουμε τους κανόνες της μορφής Α → ε κάνουμε το εξής:
Κάθε κανόνα της μορφής Β → Χ1Χ2 ... Χn τον αντικαθιστούμε με όλους τους κανόνες που προκύπτουν διαγράφοντας κάθε δυνατό υποσύνολο από εκείνα τα Χi που είναι μηδενίσιμα.
Δεν περιλαμβάνουμε όμως τον κανόνα Β → ε ακόμα και αν όλα τα Χi είναι μηδενίσιμα.
Φυσικά, ο παραπάνω αλγόριθμος μπορεί να αυξήσει κατά εκθετικό τρόπο το πλήθος των κανόνων στη νέα γραμματική.
3.4.3 Μοναδιαίοι κανόνες
Είναι επίσης δυνατό να απαλείψουμε
κάθε μοναδιαίο κανόνα της
μορφής Α → Β, όπου Α, Β
![]() V.
V.
Έστω G = (V, T, P, S) μια ΓΧΣ όπου η L(G) δεν περιλαμβάνει το ε. Μπορούμε ήδη να υποθέσουμε οτι η G δεν έχει κενούς κανόνες. Κατασκευάζουμε ένα νέο σύνολο κανόνων Ρ΄ από το Ρ ως εξής:
Πρώτα περιλαμβάνουμε όλους τους μη-μοναδιαίους κανόνες του Ρ στο Ρ΄.
Κατόπιν, ας υποθέσουμε οτι Α
Β, για Α, Β
V. Προσθέτουμε στο Ρ΄ όλους τους κανόνες της μορφής Α → w, όπου το Β → w είναι ένας μη-μοναδιαίος κανόνας του Ρ.
3.5 Κανονική μορφή του Τσόμσκι
Θεώρημα 3.5.1: Κάθε L(G) χωρίς το ε, μιας ΓΧΣ G μπορεί να παραχθεί από μια γραμματική G΄ της οποίας όλοι οι κανόνες είναι της μορφής Α → ΒC, ή Α → α, όπου τα Α, Β, και C είναι μεταβλητές, και το α τερματικό σύμβολο.
Οι γραμματικές του θεωρήματος 3.5.1 λέμε οτι είναι στην κανονική μορφή του Τσόμσκι.
Δεν θα αποδείξουμε το θεώρημα, θα δώσουμε όμως τον ακόλουθο αλγόριθμο που μετατρέπει μια ΓΧΣ σε κανονική μορφή του Τσόμσκι.
Πρώτα, βάσει των αλγορίθμων που έχουν δοθεί μέχρι στιγμής, βρίσκουμε μια ισοδύναμη γραμματική που δεν έχει κενούς κανόνες, ούτε μοναδιαίους κανόνες.
Συνεπώς αν ένας κανόνας έχει ένα μόνο σύμβολο στα δεξιά, αυτό το σύμβολο πρέπει να είναι τερματικό, άρα ο κανόνας αυτός είναι ήδη στην επιθυμητή μορφή.
Θεωρούμε τώρα κανόνες της μορφής Α
→ Χ1Χ2
... Χn
όπου n
![]() 2. Αν το Χi
είναι το τερματικό α, εισάγουμε μια νέα μεταβλητή Βα
και τον κανόνα Βα →
α, που είναι σε επιθυμητή μορφή, και αντικαθιστούμε το Χi
με το Βα. Επομένως τώρα όλοι οι κανόνες
είναι της μορφής είτε Α → α, είτε Α
→ Β1Β2
... Βn
όπου n
2. Αν το Χi
είναι το τερματικό α, εισάγουμε μια νέα μεταβλητή Βα
και τον κανόνα Βα →
α, που είναι σε επιθυμητή μορφή, και αντικαθιστούμε το Χi
με το Βα. Επομένως τώρα όλοι οι κανόνες
είναι της μορφής είτε Α → α, είτε Α
→ Β1Β2
... Βn
όπου n
![]() 2. Αν n = 2, τότε ο κανόνας είναι της
επιθυμητής μορφής. Αν n
2. Αν n = 2, τότε ο κανόνας είναι της
επιθυμητής μορφής. Αν n
![]() 3, τότε δημιουργούμε νέες μεταβλητές C1,
C2,
..., Cn–2
και αντικαθιστούμε τον κανόνα Α → Β1Β2
... Βn
με το σύνολο των κανόνων:
3, τότε δημιουργούμε νέες μεταβλητές C1,
C2,
..., Cn–2
και αντικαθιστούμε τον κανόνα Α → Β1Β2
... Βn
με το σύνολο των κανόνων:
-
Α → Β1C1
-
C1 → Β2C2
-
...
-
Cn–3 → Βn–2Cn–2
-
Cn–2 → Βn–1Βn
Το οποίο είναι σύνολο κανόνων της επιθυμητής μορφής, δηλαδή της κανονικής μορφής του Τσόμσκι.
4. Αυτόματα Στοίβας
4.1 Εισαγωγικές έννοιες και ορισμοί
Στην ενότητα 2 γνωρίσαμε τα πεπερασμένα αυτόματα και τις κανονικές εκφράσεις, και είδαμε οτι πρόκειται για μηχανισμούς που αναγνωρίζουν ένα αρκετά περιορισμένο σύνολο γλωσσών. Στην ενότητα 3 επεκτείναμε αυτό το σύνολο γλωσσών μέσω της γραμματικής χωρίς συμφραζόμενα (ΓΧΣ). Στην παρούσα ενότητα θα γνωρίσουμε έναν άλλο μηχανισμό, ένα είδος αυτομάτου, το οποίο θα έχει τις ίδιες ικανότητες με τις ΓΧΣ, θα αναγνωρίζει δηλαδή το ίδιο σύνολο γλωσσών: τις γλώσσες χωρίς συμφραζόμενα.
Ο μηχανισμός αυτός λέγεται αυτόματο στοίβας, και μοιάζει πολύ με ένα πεπερασμένο αυτόματο, συγκεκριμένα με ένα ΜΠΑ, καθώς είναι κι αυτό μη-αιτιοκρατικό, με τη διαφορά οτι περιλαμβάνει έναν επιπλέον μηχανισμό που λέγεται στοίβα. Η στοίβα είναι μια περιοχή μνήμης όπου γράφονται σε μια σειρά σύμβολα από ένα αλφάβητο, εν γένει διαφορετικό από το αλφάβητο της εισόδου του αυτομάτου. Ο τρόπος που η στοίβα ενημερώνεται με σύμβολα είναι ο εξής: σύμβολα μπορούν να εισαχθούν μόνο από το ένα άκρο της στοίβας, το οποίο θα ονομάσουμε “κορυφή”· αλλά επίσης μπορούν να διαγραφούν μόνο από την κορυφή. Έτσι, όταν ένα σύμβολο εισάγεται στη στοίβα από την κορυφή-της, είναι και το σύμβολο που έχει προτεραιότητα να εξεταστεί ή και να διαγραφεί από τη στοίβα, κάνοντας μικρότερη την προτεραιότητα όλων των άλλων συμβόλων. Η στοίβα μοιάζει με μια πραγματική στοίβα από άδεια πιάτα, από την οποία παίρνουμε πάντα το κορυφαίο πιάτο όταν χρειαζόμαστε ένα, και στην οποία βάζουμε πάντα τα νέα άδεια πιάτα από την κορυφή. Αν η στοίβα αδειάσει εντελώς, λέμε οτι αποκαλύφθηκε ο “πυθμένας” της στοίβας (ο οποίος δεν είναι σύμβολο, είναι απλώς η άδεια στοίβα). Την κενή στοίβα ια τη συμβολίζουμε με το ε.
Παράδειγμα:
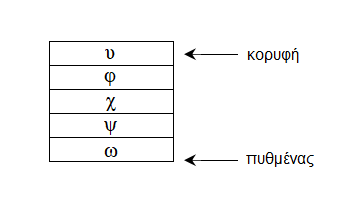
Εικ. 4.1.1: Σχηματική παράσταση στοίβας
Στο διάγραμμα 4.4.1, στην κορυφή της στοίβας βρίσκεται το σύμβολο υ, ενώ τα σύμβολα ω, ψ, χ, και φ, εισήχθησαν νωρίτερα στη στοίβα, με αυτή τη σειρά (δηλ. πρώτο το ω, μετά το ψ, κλπ). Αν το υ, που είναι στην κορυφή, διαβαστεί και αφαιρεθεί από τη στοίβα, το επόμενο σύμβολο που θα μπορεί να διαβαστεί (και ίσως να αφαιρεθεί) θα είναι το φ, κ.ο.κ. Αν προστεθεί ένα νέο σύμβολο, π.χ. το τ, αυτό θα τοποθετηθεί στην κορυφή της στοίβας, που έτσι θα μεγαλώσει κατά 1 σε μήκος. Αν ποτέ αφαιρεθεί και το ω, τότε θα αποκαλυφθεί ο πυθμένας και η στοίβα θα γίνει κενή.
Σηνειώνουμε οτι η στοίβα είναι απλώς ένας επιπλέον μηχανισμός του αυτομάτου στοίβας, που κατά τα άλλα διαθέτει και την ταινία των συμβόλων εισόδου που διαθέτει και ένα ΜΠΑ. Ας κάνουμε τώρα όλα αυτά συγκεκριμένα.
Ορισμός: Ένα αυτόματο στοίβας (ΑΣ· αγγλ.: pushdown automaton) είναι μια επτάδα (Q, Σ, Γ, δ, q0, Ζ0, F), όπου:
-
Το Q είναι ένα πεπερασμένο σύνολο καταστάσεων, όπως και στα ΠΑ.
-
Το Σ είναι ένα σύνολο συμβόλων, το αλφάβητο εισόδου, όπως και στα ΠΑ.
-
Το Γ είναι ένα σύνολο συμβόλων, το αλφάβητο στοίβας, όχι κατ’ ανάγκη διαφορετικό από το Σ.
-
Το δ είναι μια απεικόνιση από το Q X (Σ
 {ε})
X Γ σε
πεπερασμένα υποσύνολα του Q
X Γ*.
{ε})
X Γ σε
πεπερασμένα υποσύνολα του Q
X Γ*. -
Το q0
 Q είναι η αρχική κατάσταση, όπως
και στα ΠΑ.
Q είναι η αρχική κατάσταση, όπως
και στα ΠΑ. -
Το Ζ0
 Γ είναι ένα συγκεκριμένο σύμβολο που ονομάζεται
αρχικό σύμβολο στοίβας.
Γ είναι ένα συγκεκριμένο σύμβολο που ονομάζεται
αρχικό σύμβολο στοίβας. -
Τέλος, το F
 Q είναι το σύνολο των τελικών καταστάσεων,
όπως και στα ΠΑ.
Q είναι το σύνολο των τελικών καταστάσεων,
όπως και στα ΠΑ.
Θα χρησιμοποιούμε σύμβολα από την αρχή του αλφαβήτου (α, β, γ, ...) για το αλφάβητο εισόδου, και σύμβολα από το τέλος του αλφαβήτου (..., χ, ψ, ω) για το αλφάβητο στοίβας. Κατά τα άλλα, οι συμβάσεις-μας περί συμβόλων παραμένουν όπως πριν.
Αναφορικά με την απεικόνιση δ, έχουμε να πούμε τα εξής. Η γραφή:
δ (q, α, χ) = {(q1, χ1), (q2, χ2), ..., (qn, χn)}
όπου q, qi
![]() Q, 1
Q, 1
![]() i
i
![]() n, α
n, α
![]() Σ, χ
Σ, χ
![]() Γ, και χi
Γ, και χi
![]() Γ*, 1
Γ*, 1
![]() i
i
![]() n, σημαίνει οτι το ΑΣ, ευρισκόμενο σε
κατάσταση q, με α ως σύμβολο εισόδου, και χ ως
σύμβολο κορυφής της στοίβας, μπορεί να μεταφερθεί σε οποιαδήποτε
κατάσταση από τις qi,
αντικαθιστώντας το χ στη στοίβα με το αντίστοιχο χi.
Πρόκειται δηλαδή για ένα μη-αιτιοκρατικό αυτόματο. Επίσης, η
γραφή:
n, σημαίνει οτι το ΑΣ, ευρισκόμενο σε
κατάσταση q, με α ως σύμβολο εισόδου, και χ ως
σύμβολο κορυφής της στοίβας, μπορεί να μεταφερθεί σε οποιαδήποτε
κατάσταση από τις qi,
αντικαθιστώντας το χ στη στοίβα με το αντίστοιχο χi.
Πρόκειται δηλαδή για ένα μη-αιτιοκρατικό αυτόματο. Επίσης, η
γραφή:
δ (q, ε, χ) = {(q1, χ1), (q2, χ2), ..., (qn, χn)}
σημαίνει οτι το ΑΣ, ευρισκόμενο σε κατάσταση q, ανεξάρτητα από το σύμβολο εισόδου, και με το χ ως σύμβολο κορυφής της στοίβας, πράττει όπως ανωτέρω. Στην περίπτωση αυτή, η νοητή “κεφαλή” που διαβάζει την είσοδο δεν προχωράει για να διαβάσει το επόμενο σύμβολο εισόδου, αλλά παραμένει ακίνητη.
Υπάρχουν, επομένως, τα παραπάνω δύο είδη “κινήσεων” που μπορεί να κάνει ένα ΑΣ: το ένα είδος κίνησης παίρνει υπόψη τα περιεχόμενα της εισόδου, και το άλλο τα αγνοεί.
4.2 Αποδοχή γλώσσας: πότε τα ΑΣ κάνουν αποδοχή της εισόδου
Κάτι που λείπει από τον παραπάνω ορισμό είναι το πότε το ΑΣ σταματάει και αποδέχεται την είσοδο που του δόθηκε. Υπάρχουν δύο τρόποι για να σταματήσει ένα ΑΣ, που τελικά αποδεικνύεται οτι είναι ισοδύναμοι μεταξύ-τους:
-
Όπως και στα ΠΑ, δηλαδή με την άφιξη σε τελική κατάσταση q
 F. Το ΑΣ αποδέχεται τη συμβολοσειρά που το
οδήγησε στην q.
F. Το ΑΣ αποδέχεται τη συμβολοσειρά που το
οδήγησε στην q. -
Μέσω αδειάσματος της στοίβας. Όταν δηλαδή η στοίβα αδειάσει, το ΑΣ αποδέχεται τη συμβολοσειρά που το οδήγησε σε άδειασμα της στοίβας.
Αν Μ είναι το ΑΣ, τη γλώσσα της περίπτωσης 1 θα τη συμβολίζουμε με το L(Μ), ενώ τη γλώσσα της περίπτωσης 2 με το Ν(Μ).
Θεώρημα 4.2.1: Αν η γλώσσα L είναι L(M1) για κάποιο ΑΣ M1, τότε η L είναι Ν(M2) για κάποιο ΑΣ M2.
Θεώρημα 4.2.2: Αν η γλώσσα L είναι Ν(M2) για κάποιο ΑΣ M2, τότε η L είναι L(M1) για κάποιο ΑΣ M1.
Με άλλα λόγια, όπως ειπώθηκε στην εισαγωγική υποενότητα, ο τερματισμός με άφιξη σε τελική κατάσταση είναι ισοδύναμος με τον τερματισμό λόγω αδειάσματος της στοίβας. Οι αποδείξεις των δύο θεωρημάτων είναι απλές εννοιολογικά αλλά περίπλοκες στις λεπτομέρειές τους, και ο αναγνώστης μπορεί να τις βρει στο [1]· ας δει επίσης την άσκηση 4.2.1, παρακάτω.
Παράδειγμα ενός ΑΣ που τερματίζει μέσω αδειάσματος της στοίβας:

Εικ. 4.2.1: Αυτόματο Στοίβας για παλίνδρομα
Το ΑΣ της Εικ. 4.2.1 αποδέχεται τη
γλώσσα: { wwR
| w
![]() (0
+ 1)*},
δηλαδή τη γλώσσα των παλινδρόμων. Έχουμε:
Q = {q1,
q2},
Σ = {0, 1}, ενώ ως αλφάβητο στοίβας Γ χρησιμοποιούνται τρία
σύμβολα με χρώμα: {●,
●,
●} (κόκκινο,
πράσινο, μπλε). Αρχική κατάσταση είναι η q1,
αρχικό σύμβολο στη στοίβα είναι το Ζ0
= ●, ενώ το σύνολο των τελικών καταστάσεων F είναι
το
(0
+ 1)*},
δηλαδή τη γλώσσα των παλινδρόμων. Έχουμε:
Q = {q1,
q2},
Σ = {0, 1}, ενώ ως αλφάβητο στοίβας Γ χρησιμοποιούνται τρία
σύμβολα με χρώμα: {●,
●,
●} (κόκκινο,
πράσινο, μπλε). Αρχική κατάσταση είναι η q1,
αρχικό σύμβολο στη στοίβα είναι το Ζ0
= ●, ενώ το σύνολο των τελικών καταστάσεων F είναι
το ![]() (το αυτόματο τερματίζει λόγω κενής στοίβας).
(το αυτόματο τερματίζει λόγω κενής στοίβας).
Στην Εικ. 4.2.1, πάνω σε κάθε μεγάλο τόξο που αντιστοιχεί σε μια μετάβαση της δ, εμφανίζεται η περιγραφή της μετάβασης με ένα βέλος (→), αριστερά του οποίου είναι η συνθήκη της μετάβασης (το πότε γίνεται), όπως π.χ. έτσι: 0, ●→ όπου 0 είναι το σύμβολο εισόδου, ενώ το ● είναι το σύμβολο της στοίβας. Η συγκεκριμένη συνθήκη λοιπόν λέει: «Με 0 ως σύμβολο εισόδου, και ● ως σύμβολο στοίβας,...» Δεξιά του βέλους φαίνεται το τί συμβαίνει στη στοίβα. Η εισαγωγή συμβόλου στη στοίβα δείχνεται σχηματικά όποτε έχουμε δύο από τις χρωματιστές κουκκίδες–σύμβολα του Γ, τη μία πάνω στην άλλη, με την κάτω κουκκίδα να είναι αυτή που υπήρχε στην κορυφή της στοίβας, και την άνω κουκκίδα να είναι αυτή που εισάγεται και γίνεται η νέα κορυφή. Εξαγωγή από τη στοίβα έχουμε όποτε εμφανίζεται το ε δεξιά από το βέλος, δηλαδή έτσι: → ε.
Παρατηρούμε οτι το ΑΣ αυτό είναι μη-αιτιοκρατικό γιατί σε δύο περιπτώσεις από την κατάσταση q1 έχουμε δύο επιτρεπτές μεταβάσεις: τη μία με συνθήκη 0, ●, και την άλλη με συνθήκη 1, ●. Π.χ. στη συνθήκη 0, ● έχουμε τη μετάβαση στην q2 κάνοντας εξαγωγή συμβόλου από τη στοίβα (→ ε), αλλά και τη μετάβαση πίσω στην q1, εισάγοντας ένα επιπλέον ● στη στοίβα.
Η “λογική” του ΑΣ αυτού είναι, αφού ξεκινήσει τη στοίβα με ●, όποτε συναντά το 0 στην είσοδο να εισάγει στη στοίβα το ●· και όποτε συναντά το 1 στην είσοδο να εισάγει στη στοίβα το ●. Ταυτόχρονα όμως, “μαντεύει” ανά πάσα στιγμή (εδώ έγκειται η μη-αιτιοκρατικότητά του) οτι μπορεί να φτάσαμε στο μέσον του παλιδρόμου, οπότε μεταβαίνει στην q2 και αρχίζει να κάνει εξαγωγές από τη στοίβα, με το χρώμα να αναμένεται να αντιστοιχεί με το σύμβολο εισόδου: ● για 0, και ● για 1. Αν κάποια αντιστοιχία αποτύχει, το αυτόματο σταματά γιατί δεν έχει κατάλληλη μετάβαση, επομένως απορρίπτει την είσοδο («δεν είναι παλίνδρομο»). Αν όλες οι αντιστοιχίες πετύχουν και βρεθεί το ● (στον πυθμένα της στοίβας), εξάγεται και το ● και η στοίβα μένει κενή, οπότε η είσοδος γίνεται αποδεκτή («είναι παλίνδρομο»).
![]() Άσκηση 4.2.1: Έχοντας
το παραπάνω παράδειγμα κατά νου, σκεφτείτε πώς θα πρέπει να λειτουργούν
οι αποδείξεις των θεωρημάτων 4.2.1 και 4.2.2.
Άσκηση 4.2.1: Έχοντας
το παραπάνω παράδειγμα κατά νου, σκεφτείτε πώς θα πρέπει να λειτουργούν
οι αποδείξεις των θεωρημάτων 4.2.1 και 4.2.2.
4.3 Ισοδυναμία ΑΣ με ΓΧΣ
Εδώ θα διατυπώσουμε τον κύριο λόγο για τον οποίο ασχολούμαστε με τα ΑΣ: διότι αποτελούν το μηχανικό ανάλογο των γλωσσών χωρίς συμφραζόμενα. Αυτό διατυπώνεται μέσω των ακόλουθων δύο θεωρημάτων, των οποίων όμως οι αποδείξεις υπερβαίνουν το εύρος του παρόντος μαθήματος (και πάλι, ο αναγνώστης μπορεί να τις βρει στο [1]).
Θεώρημα 4.3.1: Αν η L είναι μια γλώσσα χωρίς συμφραζόμενα, τότε υπάρχει ένα ΑΣ Μ τέτοιο ώστε L = N(M).
Θεώρημα 4.3.2: Αν η γλώσσα L είναι Ν(Μ) για κάποιο ΑΣ Μ, τότε η L είναι γλώσσα χωρίς συμφραζόμενα.
Επειδή οι αποδείξεις των θεωρημάτων αυτών γίνονται πιο εύκολα όταν θεωρούμε ΑΣ με τερματισμό λόγω αδειάσματος στοίβας, αυτός είναι και ο λόγος που έχουμε ορίσει τον τερματισμό αυτόν· αλλιώς θα αρκούσε να μιλάμε για τερματισμό λόγω άφιξης σε τελική κατάσταση.
4.4 Αιτιοκρατικά ΑΣ
Η όλη παρουσίαση των ΑΣ μέχρι τώρα περιλαμβάνει μόνο μη-αιτιοκρατικές μηχανές, που αποδεικνύονται ισοδύναμες με τις ΓΧΣ.
![]() Άσκηση 4.4.1:
Τροποποιήστε τον ορισμό των ΑΣ
ώστε να ορίζει μόνο αιτιοκρατικά ΑΣ.
Άσκηση 4.4.1:
Τροποποιήστε τον ορισμό των ΑΣ
ώστε να ορίζει μόνο αιτιοκρατικά ΑΣ.
Τί συμβαίνει όμως αν περιορίσουμε τα ΑΣ ώστε να συμπεριφέρονται αιτιοκρατικά; Έχουμε μήπως τότε την ίδια κατάσταση με τα πεπερασμένα αυτόματα, όπου στην ενότητα 2 αποδείξαμε οτι αιτιοκρατικά (ΑΠΑ) και μη-αιτιοκρατικά (ΜΠΑ) αυτόματα είναι ισοδύναμα;
Η απάντηση είναι οτι όχι, στα ΑΣ αυτό
δεν συμβαίνει. Τα αιτιοκρατικά ΑΣ αποδεικνύεται οτι είναι ασθενέστερα
από τα μη-αιτιοκρατικά ΑΣ, με την έννοια οτι υπάρχουν γλώσσες χωρίς
συμφραζόμενα που αναγνωρίζονται από μη-αιτιοκρατικά ΑΣ, και για τις
οποίες δεν υπάρχει αιτιοκρατικό ΑΣ που να τις αναγνωρίζει. Παράδειγμα
μιας τέτοιας γλώσσας είναι η γλώσσα των παλινδρόμων: {
wwR |
w ![]() (0 + 1)*}.
(0 + 1)*}.
![]() Άσκηση 4.4.2:
Τροποποιήστε το παράδειγμα
της υποενότητας 4.2 ώστε να ορίσετε ένα αιτιοκρατικό ΑΣ που να
αποδέχεται τη γλώσσα {
w2wR
|
w
Άσκηση 4.4.2:
Τροποποιήστε το παράδειγμα
της υποενότητας 4.2 ώστε να ορίσετε ένα αιτιοκρατικό ΑΣ που να
αποδέχεται τη γλώσσα {
w2wR
|
w ![]() (0 + 1)*},
με Σ = {0, 1, 2}.
(0 + 1)*},
με Σ = {0, 1, 2}.
5. Μηχανές Τούρινγκ
5.1 Εισαγωγικές έννοιες και ορισμοί
Ειπώθηκε ήδη από την αρχή του παρόντος μαθήματος οτι οι μηχανές της παρούσας ενότητας, οι λεγόμενες Μηχανές Τούρινγκ, είναι μοντέλα των πιο ισχυρών υπολογιστικά μηχανών που διαθέτουμε μέχρι τώρα. Στην παρούσα ενότητα θα μάθουμε γιατί.
Ο
Άλαν Μάθισον Τούρινγκ
(Alan
Mathison Turing), που θεωρείται από πολλούς ο “πατέρας
της επιστήμης υπολογιστών”, σχεδίασε αυτό το αυτόματο–μηχανή κατά τη
δεκαετία του 1930, πριν από το 2ο Παγκόσμιο Πόλεμο, όταν δεν υπήρχαν
ακόμα οι ηλεκτρονικοί υπολογιστές. (Υπήρχαν μηχανικά κατασκευάσματα με
γρανάζια, που προσομοίαζαν με τους μετέπειτα ηλεκτρονικούς υπολογιστές,
αλλά ασύγκριτα χαμηλότερων ταχυτήτων.) Έτσι, ο Τούρινγκ σχεδίασε τη
μηχανή-του “στο χαρτί”. Παράλληλα, επινοήθηκαν και άλλα είδη αυτομάτων
από άλλους (π.χ. τα συστήματα Ποστ, από τον
Με τί μοιάζει όμως μια Μηχανή Τούρινγκ; Η ακόλουθη εικόνα μας δίνει μια ιδέα:
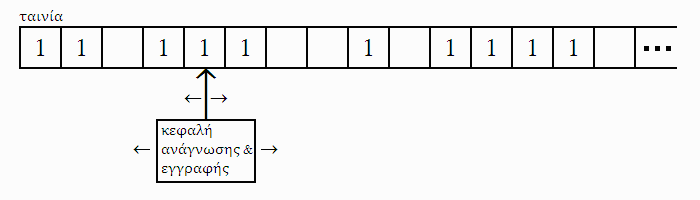
Εικ. 5.1.1: Μηχανή Τούρινγκ
Στην εικ. 5.1.1 φαίνεται σχηματικά μια Μηχανή Τούρινγκ, που περιλαμβάνει μια “ταινία” όπου αναγράφονται τόσο τα σύμβολα εισόδου, όσο και οποιαδήποτε άλλα σύμβολα προκύπτουν όσο λειτουργεί η μηχανή (στην εικόνα φαίνεται μόνο ένα σύμβολο του αλφαβήτου, το “1”), ενώ η ταινία έχει μια αρχή αλλά δεν έχει τέλος· είναι δηλαδή ατέρμονη προς τα δεξιά, περιλαμβάνοντας άπειρες θέσεις όπου μπορούν να γραφούν σύμβολα. Υπάρχει επίσης μια “κεφαλή ανάγνωσης και εγγραφής”, στην οποία μπορούμε να φανταστούμε οτι βρίσκεται το “πρόγραμμα”, δηλαδή η απεικόνιση δ που έχουμε συναντήσει στα αυτόματα έως τώρα. Η κεφαλή μπορεί να μετακινείται αριστερά ή δεξιά, και να γράφει ένα σύμβολο από το αλφάβητο στο τρέχον κελί της ταινίας, ή να αφήνει το περιεχόμενο του κελιού αμετάβλητο. Όταν η μηχανή σταματήσει (αν σταματήσει, γιατί εδώ έχουμε και το ενδεχόμενο να συνεχίσει να λειτουργεί επ’ άπειρο), τα περιεχόμενα της ταινίας αποτελούν το αποτέλεσμα, την “έξοδο” της μηχανής. Ας κάνουμε τώρα όλα αυτά πιο συγκεκριμένα.
Ορισμός: Μια Μηχανή Τούρινγκ (ΜΤ· αγγλ.: Turing Machine) είναι μια επτάδα (Q, Σ, Γ, δ, q0, ‿, F), όπου:
-
Το Q είναι ένα πεπερασμένο σύνολο καταστάσεων, όπως και στα ΠΑ.
-
Το Γ είναι ένα πεπερασμένο σύνολο συμβόλων, το αλφάβητο ταινίας.
-
Το ‿
 Γ είναι ένα συγκεκριμένο σύμβολο που ονομάζεται
κενό.
Γ είναι ένα συγκεκριμένο σύμβολο που ονομάζεται
κενό. -
Το Σ
 Γ, που δεν περιλαμβάνει το ‿, λέγεται αλφάβητο εισόδου, όπως και στα
ΠΑ.
Γ, που δεν περιλαμβάνει το ‿, λέγεται αλφάβητο εισόδου, όπως και στα
ΠΑ. -
Το δ είναι μια απεικόνιση από το Q X Γ στο Q X Γ X {Α, Δ}, όπου το Α σημαίνει “κίνηση Αριστερά”, και το Δ σημαίνει “κίνηση Δεξιά”. Η δ δεν είναι απαραίτητο να ορίζεται για όλες τις περιπτώσεις των ορισμάτων-της.
-
Το q0
 Q είναι η αρχική κατάσταση, όπως
και στα ΠΑ.
Q είναι η αρχική κατάσταση, όπως
και στα ΠΑ. -
Τέλος, το F
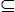 Q είναι το σύνολο των τελικών καταστάσεων,
όπως και στα ΠΑ.
Q είναι το σύνολο των τελικών καταστάσεων,
όπως και στα ΠΑ.
Η ταινία της ΜΤ είναι, όπως είπαμε, άπειρη προς τη μια κατεύθυνση (την απεικονίζουμε προς τα δεξιά), και σε κάθε κελί-της μπορεί να υπάρχει ένα μόνο σύμβολο από το Γ. Έχει ένα αρχικό κελί (απεικονίζεται στα αριστερά), και κάθε κελί έχει ένα επόμενό του (απεικονίζεται στα δεξιά-του). Η ΜΤ, όταν έχει το Α ως αποτέλεσμα της δ, αφού γράψει στο τρέχον κελί το σύμβολο του Γ που ορίζει η δ, κινεί την κεφαλή στο προηγούμενο κελί του τρέχοντος (“αριστερά”). Αντίστοιχα, όταν έχει το Δ ως αποτέλεσμα της δ, αφού γράψει στο τρέχον κελί το σύμβολο του Γ που ορίζει η δ, κινεί την κεφαλή στο επόμενο κελί του τρέχοντος (“δεξιά”).
Κατά σύμβαση, το σύμβολο ‿ για το κενό δεν θα το γράφουμε στην ταινία όταν την απεικονίζουμε σε διαγράμματα. Επομένως όταν ένα κελί εμφανίζεται χωρίς περιεχόμενα, θα θεωρούμε οτι περιλαμβάνει το κενό σύμβολο: ‿. Το ‿ θα το χρησιμοποιούμε όμως στο κείμενο, προκειμένου να αναφερθούμε στο σύμβολο “κενό” του Γ.
Παράδειγμα:
Θα φτιάξουμε μια ΜΤ που θα εκτελεί την
αφαίρεση φυσικών αριθμών. Η αφαίρεση φυσικών αριθμών ορίζεται ως εξής: αν
m και n είναι δύο
φυσικοί αριθμοί ({0, 1, 2, ...}), τότε η διαφορά-τους
m ⸛ n είναι 0 αν m < n, και
m – n (δηλ. η γνωστή διαφορά ακεραίων) αν
m
![]() n. Το αλφάβητο ταινίας Γ θα είναι το {0, 1, ‿}, με Σ = {0, 1}.
Ένας φυσικός αριθμός n θα παριστάνεται σαν μια
σειρά από n μηδενικά, δηλαδή ως 0n.
Δύο φυσικοί αριθμοί θα διαχωρίζονται μεταξύ-τους από ένα 1, οπότε η
είσοδος m ⸛ n θα παριστάνεται έτσι: 0m10n,
και το αποτέλεσμα στην ταινία όταν η ΜΤ τερματίσει θα παριστάνεται έτσι:
0m⸛n. Η ΜΤ θα
έχει 7 καταστάσεις με αρχική την q0,
οπότε μπορούμε να την περιγράψουμε μέσω επτάδας ως εξής:
n. Το αλφάβητο ταινίας Γ θα είναι το {0, 1, ‿}, με Σ = {0, 1}.
Ένας φυσικός αριθμός n θα παριστάνεται σαν μια
σειρά από n μηδενικά, δηλαδή ως 0n.
Δύο φυσικοί αριθμοί θα διαχωρίζονται μεταξύ-τους από ένα 1, οπότε η
είσοδος m ⸛ n θα παριστάνεται έτσι: 0m10n,
και το αποτέλεσμα στην ταινία όταν η ΜΤ τερματίσει θα παριστάνεται έτσι:
0m⸛n. Η ΜΤ θα
έχει 7 καταστάσεις με αρχική την q0,
οπότε μπορούμε να την περιγράψουμε μέσω επτάδας ως εξής:
Μ = ({q0, q1, q2, q3, q4, q5, q6}, {0, 1}, {0, 1, ‿}, δ, q0, ‿, {q6}).
Απομένει να ορίσουμε την απεικόνιση μεταβάσεων δ. Πριν όμως ορίσουμε τη δ τυπικά, ας περιγράψουμε τη λειτουργία αυτής της ΜΤ, δηλαδή τη “λογική” της δ.
Η Μ επαναλαμβάνει τα εξής: αντικαθιστά το πρώτο 0 που βρίσκει από αριστερά με ‿. Μετά ψάχνει προς τα δεξιά για κάποιο 1 ακολουθούμενο από 0, ώστε να εντοπίσει την αρχή του αφαιρούμενου αριθμού. Όταν την εντοπίσει, αντικαθιστά το 0 με 1. Στη συνέχεια η Μ μετακινεί την κεφαλή αριστερά μέχρι να βρει ένα ‿, και επαναλαμβάνει τον κύκλο. Η ανακύκλωση τελειώνει όταν:
-
Αν ψάχνοντας δεξιά για ένα 0, η Μ βρίσκει ένα ‿. Τότε, τα n 0 στο αρχικό 0m10n έχουν όλα μετατραπεί σε 1, όπως και n+1 από τα m 0 στο 0m10n έχουν μετατραπεί σε ‿. Η Μ αντικαθιστά τα n+1 1 με ένα 0 και n ‿, αφήνοντας m – n 0 στην ταινία-της.
-
Αν ξεκινώντας την ανακύκλωση, η Μ δεν μπορεί να βρει ένα 0 για να το αντικαταστήσει με ‿, γιατί τα πρώτα m 0 έχουν ήδη αντικατασταθεί. Αυτό συμβαίνει όταν n
 m, οπότε m ⸛ n = 0. Τότε η Μ
αντικαθιστά όλα τα εναπομείναντα 1 και 0 με ‿.
m, οπότε m ⸛ n = 0. Τότε η Μ
αντικαθιστά όλα τα εναπομείναντα 1 και 0 με ‿.
Θα δώσουμε τη δ παρακάτω με τη μορφή κειμένου και όχι με τη μορφή γράφου, γιατί οι μεταβάσεις είναι αρκετές στον αριθμό, οπότε ο γράφος θα ήταν οπτικά αρκετά περίπλοκος.
-
δ (q0, 0) = (q1, ‿, Δ)
Αρχή της ανακύκλωσης. Αντικατάσταση του αρχικού (αριστερότερου) 0 με ‿. -
δ (q1, 0) = (q1, 0, Δ)
δ (q1, 1) = (q2, 1, Δ)
Ψάξιμο δεξιά για το πρώτο 1. -
δ (q2, 1) = (q2, 1, Δ)
δ (q2, 0) = (q3, 1, Α)
Ψάξιμο δεξιά μετά το 1, μέχρι να βρεθεί ένα 0. Αλλαγή εκείνου του 0 σε 1. -
δ (q3, 0) = (q3, 0, Α)
δ (q3, 1) = (q3, 1, Α)
δ (q3, ‿) = (q0, ‿, Δ)
Μετακίνηση αριστερά μέχρι το κενό. Αλλαγή σε κατάσταση q0 ώστε να γίνει η ανακύκλωση. -
δ (q2, ‿) = (q4, ‿, Α)
δ (q4, 1) = (q4, ‿, Α)
δ (q4, 0) = (q4, 0, Α)
δ (q4, ‿) = (q6, 0, Δ)
Αν το ‿ εμφανίζεται προ ενός 0 σε κατάσταση q2, αλλάζουμε σε κατάσταση q4 και μεταφερόμαστε αριστερά, αλλάζοντας όλα τα 1 σε ‿ μέχρι να συναντήσουμε ένα ‿. Αυτό το ‿ αλλάζει σε 0, αλλάζουμε σε κατάσταση q6, και η Μ τερματίζει. -
δ (q0, 1) = (q5, ‿, Δ)
δ (q5, 0) = (q5, ‿, Δ)
δ (q5, 1) = (q5, ‿, Δ)
δ (q5, ‿) = (q6, ‿, Δ)
Αν στην κατάσταση q0 εμφανιστεί το 1 αντί για το 0, η πρώτη ακολουθία των 0 έχει εξαντληθεί, οπότε η Μ μπαίνει στην κατάσταση q5 ώστε να σβήσει όλη την υπόλοιπη ταινία. Κατόπιν μπαίνει σε κατάσταση q6 και τερματίζει.
Δεδομένης της εισόδου 0010, η παραπάνω ΜΤ Μ θα πρέπει να αφήσει στην ταινία το ‿0. Τα διαδοχικά στάδια είναι τα εξής:
q00010 → ‿q1010 → ‿0q110 → ‿01q20 →
‿0q311 → ‿q3011 → q3‿011 → ‿q0011 →
‿‿q111 → ‿‿1q21 → ‿‿11q2 → ‿‿1q41 →
‿‿q41 → ‿q4 → ‿0q6
Δεδομένης της εισόδου 0100, η Μ θα πρέπει να αφήσει την ταινία αποτελούμενη από ‿. Τα διαδοχικά στάδια είναι τα εξής:
q00100 → ‿q1100 → ‿1q200 → ‿q3110 →
q3‿110 → ‿q0110 → ‿‿q510 → ‿‿‿q50 →
‿‿‿‿q5 → ‿‿‿‿‿q6
Παρατηρούμε οτι αν ακολουθούν επιπλέον σύμβολα στην ταινία (αν δηλαδή η είσοδος δεν είναι της μορφής 0m10n) τότε η παραπάνω ΜΤ θα τερματίσει απορρίπτοντας τη συμβολοσειρά εισόδου-της, γιατί δεν δεν υπάρχουν καθόλου μεταβάσεις από την κατάσταση q6. Πάντως αν ο σκοπός είναι απλώς να κατασκευαστεί η έξοδος στην ταινία (δηλαδή το 0m⸛n). τότε δεν είναι απαραίτητο να ορίσουμε τελική κατάσταση, γιατί δεν ενδιαφερόμαστε για την αποδοχή ή απόρριψη της συμβολοσειράς εισόδου.
Και μία μετα-παρατήρηση είναι οτι για μια τόσο απλή πράξη όπως η m ⸛ n απαιτήθηκε ένα αρκετά πολύπλοκο αυτόματο ώστε να την υλοποιήσει. Αυτό είναι γενική παρατήρηση: απαιτείται πολύς “κόπος” προκειμένου να “προγραμματίσουμε” μια ΜΤ. Για το λόγο αυτό θα σημειώσουμε τώρα μερικές τεχνικές που συντομεύουν την κατασκευή Μηχανών Τούρινγκ.
5.2 Νοητές συντομεύσεις Μηχανών Τούρινγκ
Θα εξετάσουμε εδώ κάποιες “συμβάσεις” που μπορούμε να κάνουμε (με τον εαυτό-μας), ώστε χωρίς να τροποποιήσουμε τον ορισμό της ΜΤ, να μπορούμε να συντομεύσουμε τις υλοποιήσεις των αυτομάτων αυτών.
5.2.1 Αποθήκευση συμβόλων σε καταστάσεις
Ας θεωρήσουμε το εξής πρόβλημα: να κατασκευαστεί ΜΤ τέτοια ώστε να ελέγχει το πρώτο (πιο αριστερό) σύμβολο της ταινίας-της, και αν αυτό δεν εμφανίζεται ξανά στην ταινία να αποδέχεται τη συμβολοσειρά εισόδου, αλλιώς να την απορρίπτει.
Βεβαίως για το πρόβλημα αυτό αρκεί και ένα αιτιοκρατικό πεπερασμένο αυτόματο (ΑΠΑ)· αλλά θα κατασκευάσουμε εδώ μια ΜΤ χάριν παραδείγματος.
Η ιδέα είναι να χρησιμοποιήσουμε το σύνολο καταστάσεων, διευρύνοντάς το, ώστε εκτός από μια απλή κατάσταση (π.χ. “q0”), η “διευρυμένη κατάσταση” να “θυμάται” και ένα σύμβολο που διαβάστηκε από την ταινία. Έτσι, η “διευρυμένη κατάσταση” θα είναι ένα ζεύγος, όπως το [q0, 1], που θα σημαίνει οτι “είμαστε σε κατάσταση q0 ενώ έχει διαβαστεί ως πρώτο από αριστερά σύμβολο το 1”. Ολόκληρο το [q0, 1] θα είναι η ετικέτα για μια κατάσταση της ΜΤ.
Συγκεκριμένα, η ΜΤ αυτή θα είναι η εξής επτάδα:
Μ = (Q, {0, 1}, {0, 1, ‿}, δ, [q0, ‿], ‿, {[q1, ‿]})
όπου το Q είναι το σύνολο {q0, q1} X {0, 1, ‿}. Επομένως, αναλυτικά το Q είναι: {[q0, 0], [q0, 1], [q0, ‿], [q1, 0], [q1, 1], [q1, ‿]}.
Η απεικόνιση δ τώρα, ορίζεται ως εξής:
-
α) δ ([q0, ‿], 0) = ([q1, 0], 0, Δ)
β) δ ([q0, ‿], 1) = ([q1, 1], 1, Δ)
Αυτές οι μεταβάσεις έχουν την εννοια οτι το σύμβολο που συναντάται πρώτο στην ταινία (0 ή 1) “αποθηκεύεται” στην κατάσταση (ως το δεύτερο μέλος του ζεύγους), και η ΜΤ προχωρά σε κατάσταση q1, “ενθυμούμενη” όμως το σύμβολο που διαβάστηκε (πάντα ως δεύτερο μέλος του ζεύγους). -
α) δ ([q1, 0], 1) = ([q1, 0], 1, Δ)
β) δ ([q1, 1], 0) = ([q1, 1], 0, Δ)
Αν το αποθηκευμένο σύμβολο διαφωνεί με το τρέχον σύμβολο της ταινίας, όλα πάνε καλά και προχωρούμε προς τα δεξιά. -
α) δ ([q1, 0], ‿) = ([q1, ‿], 0, Α)
β) δ ([q1, 1], ‿) = ([q1, ‿], 0, Α)
Αν η Μ συναντήσει κενό χωρίς προηγουμένως να έχει συναντήσει το σύμβολο που “θυμάται” μέσω των καταστάσεών της, τότε μεταβαίνει στην τελική κατάσταση [q1, ‿].
Αν βεβαίως η Μ συναντήσει στην ταινία το σύμβολο που “θυμάται” μέσω καταστάσεων, τότε θα τερματίσει με απόρριψη, γιατί η δ δεν ορίζεται σε μια τέτοια περίπτωση.
Πιο γενικά, μπορούμε να αποθηκεύσουμε σε καταστάσεις όσα σύμβολα επιθυμούμε, πολλαπλασιάζοντας βέβαια με τον τρόπο αυτό τον αριθμό των καταστάσεων.
5.2.2 Ταινία με πολλαπλές “τροχιές”
Θεωρούμε τώρα το πρόβλημα της απόφασης του αν ένας φυσικός αριθμός (δοσμένος στο δυαδικό σύστημα) είναι πρώτος ή σύνθετος. Το πρόβλημα αυτό δεν μπορεί να λυθεί μέσω ΑΣ, πόσω μάλλον μέσω ΠΑ. Θα το λύσουμε μέσω μιας ΜΤ που η ταινία-της έχει τρεις “τροχιές”, ή “ράγες”, αντί για μία, όπως δείχνει η Εικ. 5.2.2.1. Πρέπει να γίνει κατανοητό όμως οτι αυτές οι τροχιές είναι νοητά κατασκευάσματα, όπως θα δούμε· δεν θα χρειαστεί να αλλάξουμε καθόλου τον ορισμό της ΜΤ.
Εικ. 5.2.2.1: ΜΤ τριών τροχιών
Στην πρώτη τροχιά θα είναι αποθηκευμένη η συμβολοσειρά εισόδου που παριστάνει το φυσικό αριθμό στο δυαδικό σύστημα. Οι δυαδικοί αριθμοί όμως, και στις τρεις τροχιές, είναι πιο βολικό να παριστάνονται με αντίστροφη σειρά των ψηφίων-τους από αυτή με την οποία κανονικά τους παριστάνουμε· δηλαδή, το πρώτο από αριστερά ψηφίο θα είναι ο πολλαπλασιαστής του 20, το δεύτερο ο πολλαπλασιαστής του 21, κ.ο.κ. Αυτό διευκολύνει τη διαδικασία αύξησης του αριθμού κατά 1, που απαιτείται στη 2η τροχιά. Έτσι, ο αριθμός που παριστάνεται στην 1η τροχιά της Εικ. 5.2.2.1 είναι ο 53, ενώ εκείνος στην 3η τροχιά είναι ο 50.
Στη δεύτερη τροχιά θα αποθηκεύεται ο διαιρέτης του δοσμένου αριθμού της 1ης τροχιάς. Ο διαιρέτης αυτός θα αυξάνεται κατά ένα, μέχρις ότου βρεθεί οτι διαιρεί ακριβώς το δοσμένο αριθμό (μέσω της διαδικασίας που εξηγείται αμέσως παρακάτω), οπότε ο δοσμένος αριθμός δεν είναι πρώτος (είναι σύνθετος), ή οτι έχει γίνει ίσος με το δοσμένο αριθμό, οπότε έχουμε πρώτο αριθμό στην είσοδο. Βέβαια η διαδικασία αυτή δεν είναι και η πιο αποδοτική, καθώς κανονικά αρκεί να φτάσουμε μέχρι την τετραγωνική ρίζα του δοσμένου αριθμού προκειμένου να αποφασίσουμε αν έχει διαιρέτες, και όχι μέχρι τον ίδιο τον αριθμό· αλλά ο σκοπός-μας εδώ είναι απλώς να λύσουμε το πρόβλημα, και όχι να το λύσουμε με τον πιο αποδοτικό τρόπο.
Τέλος, στην τρίτη τροχιά γίνεται ένα αντίγραφο του δοσμένου αριθμού από την 1η τροχιά, και ο αριθμός της 2ης τροχιάς αφαιρείται επαναληπτικά από εκείνον της 3ης τροχιάς. Έτσι, αν μετά από διαδοχικές αφαιρέσεις έχουμε σαν αποτέλεσμα το ‿ στην 3η τροχιά (που είναι η παράσταση του μηδενός), τότε ο διαιρέτης (αριθμός της 2ης τροχιάς) διαιρεί ακριβώς τον δοσμένο. Αν όχι, κάνουμε ένα καινούργιο αντίγραφο του δοσμένου από την 1η στην 3η τροχιά, αυξάνουμε το διαιρέτη κατά 1, και επαναλαμβάνουμε τη διαδικασία.
Μένει τώρα να δούμε πώς μπορούμε να υλοποιήσουμε τις πολλαπλές τροχιές σε μια ΜΤ χωρίς να τροποποιήσουμε τον ορισμό-της. Υπάρχουν τουλάχιστον τρεις τρόποι:
-
Ένας τρόπος είναι αυξάνοντας το αλφάβητο της ταινίας ώστε, αν π.χ. θέλουμε να έχουμε τρεις τροχιές, το αλφάβητο να περιλαμβάνει όλους τους δυνατούς συνδυασμούς ψηφίων, συμπεριλαμβανομένου και του κενού, σε τρεις θέσεις. Δηλαδή, το αλφάβητο θα είναι το: 000, 001, 010, 011, ... 00‿, 0‿0, 0‿‿, ... Οπότε χρειάζεται να “μεταφράσουμε” κάθε δυνατή περίπτωση συμβόλου εισόδου στο τί θα πρέπει να συμβαίνει στο σύμβολο αυτό σύμφωνα με τη λογική του προγράμματός μας. Η μέθοδος αυτή όμως είναι εξαιρετικά επίπονη, και μάλλον προσθέτει παρά αφαιρεί πολυπλοκότητα.
-
Άλλος τρόπος είναι να θεωρήσουμε οτι: το 1ο ψηφίο της 1ης τροχιάς είναι στην 1η θέση της απλής ταινίας της ΜΤ· το 1ο ψηφίο της 2ης τροχιάς είναι στη 2η θέση της απλής ταινίας· το 1ο ψηφίο της 3ης τροχιάς είναι στην 3η θέση της απλής ταινίας· στη συνέχεια, το 2ο ψηφίο της 1ης τροχιάς είναι στην 4η θέση της απλής ταινίας· κ.ο.κ. Αυτό σημαίνει οτι κάθε φορά που θέλουμε το ν-στό ψηφίο κάποιας τροχιάς θα πρέπει να κάνουμε τη ΜΤ να εκτελεί μια διαδρομή πάνω στην απλή ταινία, ώσπου να βρίσκει το ψηφίο στη σωστή θέση πάνω στην απλή ταινία. Αυτή η λύση είναι λιγότερο πολύπλοκη από την προηγούμενη.
-
Άλλος τρόπος είναι να παραθέσουμε στην απλή ταινία τους αριθμούς που επιθυμούμε, τον ένα μετά τον άλλον, χωρίζοντάς τους με κάποιο ειδικό σύμβολο ή σύμβολα που προσθέτουμε στο αλφάβητο Γ της ταινίας. Αυτή η λύση είναι εφικτή όταν οι αριθμοί δεν αυξάνουν πέρα από ένα ορισμένο μήκος όσο δουλεύει η ΜΤ, όπως ισχύει στο παραπάνω πρόβλημα, οπότε τότε η λύση αυτή είναι και η πιο απλή.
Επομένως, μέσω της παραπάνω λύσης (2η ή 3η περίπτωση) αυξάνουμε το πρόγραμμα (γιατί πρέπει να βάλουμε τη ΜΤ να κάνει “διαδρομές” πάνω στην απλή ταινία προκειμένου να εντοπίσει το σωστό ψηφίο), αλλά κερδίζουμε σε απλότητα κατανόησης της περιγραφής του προγράμματος (της δ).
5.2.3 Μαρκάρισμα συμβόλων
Σε ορισμένες περιπτώσεις είναι βολικό να μπορούμε να “μαρκάρουμε” κάποιο σύμβολο ή σύμβολα στην ταινία, ως “αναγνωσμένο”, “αναγνωρισμένο”, “σύμβολο που έχει ιδωθεί”, κλπ· να κάνουμε δηλαδή το αντίστοιχο του να βάζουμε ένα σύμβολο √ πάνω στο σύμβολο της ταινίας.
Αντί να βάζουμε το √ πάνω στην ταινία, που δεν είναι επιθυμητό γιατί έτσι αλλοιώνουμε τη συμβολοσειρά εισόδου, μπορούμε να θεωρήσουμε οτι έχουμε ΜΤ με μια δεύτερη τροχιά, στην οποία βάζουμε το √ “κάτω” ακριβώς από το σύμβολο που θέλουμε να μαρκάρουμε, όπως στο διάγραμμα της Εικ. 5.2.3.1.
Εικ. 5.2.3.1: Μαρκάρισμα συμβόλων σε επιπλέον τροχιά
Στην Εικ. 5.2.3.1 φαίνεται μια ΜΤ που
βρίσκεται στη διαδικασία αναγνώρισης εισόδου από τη γλώσσα {
ww | w
![]() (0 + 1)*}.
(0 + 1)*}.
Άσκηση 5.2.1:
Δώστε μια λεκτική περιγραφή της απεικόνισης δ της παραπάνω ΜΤ που
αναγνωρίζει τη γλώσσα { ww | w
![]() (0 + 1)*}.
(0 + 1)*}.
5.2.4 Αντιγραφή – επικόλληση τμημάτων συμβόλων
Σε άλλες περιπτώσεις είναι χρήσιμο να γίνεται η διαδικασία “αντιγραφής – επικόλλησης” συμβόλων επί της ταινίας, ή και “διαγραφής – επικόλλησης”, ανάλογα με το πρόβλημα.
Άσκηση 5.2.2: Περιγράψετε λεκτικά το πώς μπορεί να λυθεί το πρόβλημα του πολλαπλασιασμού φυσικών αριθμών n · m μέσω αντιγραφής – επικόλλησης, όπου στην ταινία εισόδου ο πολλαπλασιαστής και ο πολλαπλασιαστέος παριστάνονται ως 1n‿1m‿, ενώ το ζητούμενο γινόμενο παριστάνεται ως 1nm‿. Δηλαδή το Σ = { 1 }.
5.2.5 Υποπρογράμματα (ή διαδικασίες)
Από το ξεκίνημα της εκμάθησης προγραμματισμού γίνεται εισαγωγή στην έννοια του “υποπρογράμματος” ή “διαδικασίας”. Είναι εύκολο να οριοθετήσουμε ένα τμήμα της δ μιας ΜΤ και να το κάνουμε να λειτουργεί ως υποπρόγραμμα, ως εξής:
Το τμήμα αυτό της δ πρέπει να έχει μια καθορισμένη αρχική κατάσταση και μια καθορισμένη τελική κατάσταση. Η τελική κατάσταση πρέπει να έχει μια μετάβαση επιστροφής προς την κατάσταση της καλούσας διαδικασίας. Αυτή είναι η απλούστατη περίπτωση ενός υποπρογράμματος χωρίς παραμέτρους, επομένως χωρίς στοίβα η οποία να υλοποιεί το πέρασμα ορισμάτων στις παραμέτρους. Αλλά κι αν υπάρχουν παράμετροι, μπορεί να γίνει προσομοίωση της στοίβας σε δύο επιπλέον τροχιές: μία για τα περιεχόμενα της στοίβας, και μία για ένα δείκτη που να “δείχνει” προς την ανά πάσα στιγμή κορυφή της στοίβας.
5.3 Μηχανές Τούρινγκ με αυξημένα χαρακτηριστικά
Όλες οι προηγούμενες τροποποιήσεις ήσαν νοητές, δηλαδή διατηρώντας τον ίδιο ορισμό της ΜΤ, είδαμε πώς θα μπορούσαμε να φανταστούμε τη μηχανή από υψηλότερο επίπεδο, ώστε να υλοποιεί κάποια χαρακτηριστικά που θα επιθυμούσαμε να έχει. Τώρα θα δούμε πραγματικές τροποποιήσεις στον ορισμό, που θα προσθέτουν πραγματικά επιπλέον χαρακτηριστικά. Θα διαπιστώσουμε όμως οτι καμία από τις ΜΤ με τα αυξημένα χαρακτηριστικά δεν έχει μεγαλύτερη υπολογιστική ικανότητα από την απλή ΜΤ που ήδη γνωρίσαμε. Σε κάθε περίπτωση, η απλή ΜΤ θα μπορεί να προσομοιώνει τη σύνθετη ΜΤ.
5.3.1 Ταινία άπειρη και προς τις δύο διευθύνσεις
Είπαμε οτι η ταινία μιας ΜΤ, στον αρχικό ορισμό, είναι άπειρη προς τη μία διεύθυνση (προς τα “δεξιά” όπως την απεικονίζουμε). Μήπως μια ΜΤ θα μπορούσε να αναγνωρίσει ένα πιο πλούσιο σύνολο γλωσσών αν η ταινία-της ήταν άπειρη και προς τις δύο διευθυνσεις (και προς τα “αριστερά” όπως την απεικονίζουμε); Το επόμενο θεώρημα δείχνει οτι αυτό δεν συμβαίνει.
Θεώρημα 5.3.1: Έστω μία γλώσσα L, και μία ΜΤ Μ2 με ταινία άπειρη και προς τις δύο διευθύνσεις. Η L αναγνωρίζεται από την Μ2 τότε και μόνο τότε όταν υπάρχει μία ΜΤ Μ1 με απλή ταινία άπειρη προς τη μία διεύθυνση που αναγνωρίζει την L.
|
Υπόδειξη απόδειξης. Το οτι η Μ2 μπορεί να προσομοιώσει τη Μ1 είναι αρκετά προφανές: η ταινία της Μ1 αντιγράφεται στο “ήμισυ” της ταινίας της Μ2, με ένα επιπλέον σύμβολο (π.χ. το #) εκτός του αλφαβήτου της Μ1. Η Μ2 αντιγράφει τις κινήσεις της Μ1, όπως και τις μεταβολές στο ήμισυ της ταινίας. Αν η Μ2 χρειαστεί να ξεπεράσει το σύμβολο # ή να γράψει επάνω-του, τότε τερματίζει απορρίπτοντας τη συμβολοσειρά εισόδου. Η Μ2 τερματίζει με αποδοχή όταν και η Μ1 τερματίσει με αποδοχή. Για την αντίστροφη προσομοίωση τώρα, δηλαδή της Μ2 από τη Μ1, που είναι και συγκριτικά η πιο δύσκολη, κάνουμε το εξής: Μετατρέπουμε τη Μ1 σε ΜΤ με δύο τροχιές. Στην 1η τροχιά αντιγράφουμε το ήμισυ της ταινίας της Μ2 από το αρχικό κελί της κεφαλής και πέρα, ενώ στη 2η τροχιά αντιγράφουμε το υπόλοιπο ήμισυ της Μ2, από τη θέση πριν από το αρχικό κελί της κεφαλής και “πίσω”, όπως στην εικόνα 5.3.1.1.
Εικ. 5.3.1.1: Προσομοίωση ΜΤ με διπλά άπειρη ταινία Όταν η κεφαλή της Μ2 είναι στα δεξιά του αρχικού κελιού Α0 της ταινίας, η Μ1 δουλεύει στην επάνω τροχιά· ενώ όταν η κεφαλή της Μ2 είναι στα αριστερά του Α0, η Μ1 δουλεύει στην κάτω τροχιά, κινούμενη προς διεύθυνση αντίθετη από εκείνη προς την οποία κινείται η Μ2. Αυτή είναι η γενική ιδέα της απόδειξης, ενώ οι λεπτομέρειες του ακριβούς ορισμού της δ αφήνονται για τον ενδιαφερόμενο αναγνώστη. (Δίνεται με κάθε λεπτομέσεια στο [1].) ▓ |
5.3.2 Μηχανή Τούρινγκ με πολλαπλές ταινίες και κεφαλές
Μια ΜΤ μπορεί να έχει όχι απλώς διαφορετικές τροχιές και μία κεφαλή, αλλά πολλαπλές ταινίες με διαφορετική κεφαλή να διαβάζει–γράφει σε κάθε ταινία, η οποία να είναι άπειρη και προς τις δύο διευθύνσεις.
Και πάλι, μπορούμε να προσομοιώσουμε
μια τέτοια ΜΤ με k ταινίες και κεφαλές,
μέσω μιας απλής ΜΤ με ταινία άπειρη προς τη μία διεύθυνση. Αρκεί η
“απλή” αυτή ΜΤ να έχει 2k τροχιές
άπειρες και προς τις δύο διευθύνσεις (όπου οι προηγούμενες υποενότητες
υποδεικνύουν πώς είναι αυτό δυνατό). Η τροχιά 2i–1
προσομοιώνει την ταινία 2i, (1
![]() i
i
![]() k), ενώ η τροχιά 2i
σημειώνει (με “μαρκάρισμα συμβόλου”, βλέπε
§5.2.3) τη θέση της κεφαλής στην ταινία
2i.
k), ενώ η τροχιά 2i
σημειώνει (με “μαρκάρισμα συμβόλου”, βλέπε
§5.2.3) τη θέση της κεφαλής στην ταινία
2i.
5.3.3 Μη αιτιοκρατικές Μηχανές Τούρινγκ
Όπως και στα πεπερασμένα αυτόματα, έτσι και στις ΜΤ (αλλά σε αντίθεση με τα ΑΣ), αποδεικνύεται οτι η μη αιτιοκρατική ΜΤ μπορεί να προσομοιωθεί από μια αιτιοκρατική ΜΤ.
Θεώρημα 5.3.2: Αν η γλώσσα L γίνεται αποδεκτή από μια μη-αιτιοκρατική ΜΤ Μ2, τότε η L μπορεί να γίνει αποδεκτή από μια αιτιοκρατική ΜΤ Μ1.
|
Απόδειξη. Για κάθε κατάσταση και σύμβολο ταινίας της Μ2 υπάρχει ένας πεπερασμένος αριθμός επιλογών για την επόμενη κίνηση. Οι επιλογές αυτές μπορούν να αριθμηθούν: 1, 2, ... Έστω r ο μέγιστος αριθμός επιλογών για οποιοοδήποτε ζεύγος [κατάσταση, σύμβολο ταινίας]. Τότε, οποιαδήποτε πεπερασμένη ακολουθία από επιλογές μπορεί να παρασταθεί από μια ακολουθία ψηφιων από το 1 ως το r. Δεν θα αντιπροσωπεύει η κάθε δυνατή τέτοια ακολουθία μια επιλογή κινήσεων, αφού μπορεί να υπάρχουν λιγότερες από r επιλογές σε κάποιες περιπτώσεις. Η Μ1 θα έχει 3 ταινίες (σύμφωνα με την §5.3.2). Η πρώτη ταινία θα περιέχει την είσοδο. Στη δεύτερη ταινία, η Μ1 θα δημιουργήσει όλες τις ακολουθίες ψηφίων από το 1 ως το r με ένα συστηματικό τρόπο. Συγκεκριμένα, οι ακολουθίες θα δημιουργηθούν κατά αύξουσα σειρά μήκους. Ακολουθίες ίσου μήκους μπορούν να δημιουργηθούν κατά αριθμητική σειρά. Για κάθε ακολουθία που έχει δημιουργηθεί στην ταινία 2, η Μ1 αντιγράφει την είσοδο στην ταινία 3, και μετά προσομοιώνει τη Μ2 στην ταινία 3, χρησιμοποιώντας την ακολουθία στην ταινία 2 για να πραγματοποιήσει τις κινήσεις της Μ2. Αν η Μ2 περάσει σε τελική κατάσταση και αποδεχτεί την είσοδο, η Μ1 αποδέχεται επίσης την είσοδο. Αν υπάρχει ακολουθία επιλογών που οδηγεί σε αποδοχή, αυτή η ακολουθία θα δημιουργηθεί τελικά στην ταινία 2. Όταν αυτή η ακολουθία προσομοιωθεί, η Μ1 θα τερματίσει αποδεχόμενη. Αλλά αν καμία ακολουθία επιλογών κινήσεων της Μ2 δεν οδηγεί σε αποδοχή, η Μ1 δεν θα αποδεχτεί την είσοδο. ▓ |
5.3.4 Μηχανές Τούρινγκ με αυθαίρετα μεγάλα αλφάβητα
Είναι μάλλον προφανές οτι αυξάνοντας τα στοιχεία του αλφαβήτου δεν αυξάνουμε τις ικανότητες της ΜΤ. Αυτό συνοψίζεται στο παρακάτω θεώρημα:
Θεώρημα 5.3.3: Αν η γλώσσα
L γίνεται αποδεκτή από μια ΜΤ Μ με αλφάβητο Σ,
όπου | Σ |
![]() 3, τότε γίνεται αποδεκτή και από μια ΜΤ Μ1
με αλφάβητο Σ1 = {0, 1}.
3, τότε γίνεται αποδεκτή και από μια ΜΤ Μ1
με αλφάβητο Σ1 = {0, 1}.
|
Απόδειξη. Απαριθμούμε τα στοιχεία του Σ κατά μια οποιαδήποτε σειρά (το Σ είναι απαριθμήσιμο, εφόσον είναι πεπερασμένο), και εκχωρούμε έναν αύξοντα αριθμό σε κάθε στοιχείο της ακολουθίας αυτής. Τον αύξοντα αριθμό αυτόν τον παριστάνουμε στη δυαδική-του μορφή, επομένως μέσω του αλφαβήτου Σ1 = {0, 1}. Στον ορισμό της Μ αντικαθιστούμε τα στοιχεία του Σ μέσω της αντιστοίχισης που κάναμε από το Σ1, οπότε προκύπτει η Μ1. ▓ |
Το αποτέλεσμα αυτό θα το χρειαστούμε στην §5.6, όταν θα θεωρήσουμε ΜΤ στη γενικότητά τους, και θα τις κωδικοποιήσουμε.
5.4 Αποφασίσιμες γλώσσες και υπολογιζόμενες συναρτήσεις
5.4.1 Αποφασίσιμες, ημιαποφασίσιμες, και αναποφασίσιμες γλώσσες
Ορισμός: Μια γλώσσα για την οποία υπάρχει ΜΤ που να την αποδέχεται ονομάζεται αναδρομικά απαριθμήσιμη (α.α.) γλώσσα.
Ο όρος “απαριθμήσιμη” αναφέρεται στο γεγονός οτι πρόκειται για εκείνες τις γλώσσες των οποίων τα στοιχεία μπορεί να απαριθμήσει (να δημιουργήσει στη σειρά, το ένα μετά το άλλο) μια ΜΤ. Ο όρος “αναδρομικά” προέρχεται από εποχή προ της ύπαρξης των υπολογιστών, και είναι παρόμοιος με αυτό που εννοούμε στην επιστήμη υπολογισμών όταν μιλάμε για “αναδρομή”: μια διαδικασία να καλεί (άμεσα ή έμμεσα) τον εαυτό-της. Το σύνολο των α.α. γλωσσών είναι το πιο ευρύ σύνολο για το οποίο μπορούμε να κατασκευάσουμε μηχανές (δηλαδή τις ΜΤ) που να αποδέχονται (ή να δημιουργούν) τα στοιχεία-του, και είναι γνήσιο υπερσύνολο του συνόλου των γλωσσών χωρίς συμφραζόμενα.
Το σύνολο των α.α. γλωσσών
περιλαμβάνει κάποια μέλη (γλώσσες) για τα οποία δεν μπορούμε να
αποφασίσουμε μηχανικά αν μια συμβολοσειρά είναι μέλος-τους ή όχι. Αν η
L είναι μια τέτοια γλώσσα, τότε κάθε ΜΤ που
αποδέχεται την L πρέπει να αποτυγχάνει να
τερματίσει για κάποια συμβολοσειρά x
που δεν ανήκει στην L. Αν η συμβολοσειρά
y
![]() L, τότε η ΜΤ τελικά θα τερματίσει και θα
αποδεχτεί την y. Όσο όμως η ΜΤ
συνεχίζει να λειτουργεί δοσμένης κάποιας συμβολοσειράς εισόδου, δεν
μπορούμε ποτέ να ξέρουμε αν η ΜΤ τελικά θα σταματήσει αποδεχόμενη τη
συμβολοσειρά, ή θα συνεχίσει να λειτουργεί επ’ άπειρο, μη δίνοντας
απάντηση.
L, τότε η ΜΤ τελικά θα τερματίσει και θα
αποδεχτεί την y. Όσο όμως η ΜΤ
συνεχίζει να λειτουργεί δοσμένης κάποιας συμβολοσειράς εισόδου, δεν
μπορούμε ποτέ να ξέρουμε αν η ΜΤ τελικά θα σταματήσει αποδεχόμενη τη
συμβολοσειρά, ή θα συνεχίσει να λειτουργεί επ’ άπειρο, μη δίνοντας
απάντηση.
Ορισμός: Μια γλώσσα για την οποία υπάρχει ΜΤ που τερματίζει πάντα και αποφασίζει αν μια συμβολοσειρά ανήκει ή δεν ανήκει στη γλώσσα, λέγεται αποφασίσιμη, ή αλλιώς, αναδρομικό σύνολο.
Ορισμός: Μια γλώσσα για την οποία υπάρχει ΜΤ που τερματίζει αποφασίζοντας αν μια συμβολοσειρά ανήκει στη γλώσσα, αλλά η ΜΤ αυτή μπορεί να συνεχίσει να λειτουργεί επ’ άπειρο (χωρίς να γνωρίζουμε αν ποτέ θα τερματίσει) αν της δοθεί μια συμβολοσειρά που δεν ανήκει στη γλώσσα, ονομάζεται ημιαποφασίσιμη.
Ορισμός: Μια γλώσσα για την οποία δεν υπάρχει ΜΤ που να αποφασίζει τερματίζοντας αν μια συμβολοσειρά ανήκει ή δεν ανήκει στη γλώσσα, ονομάζεται αναποφασίσιμη.
5.4.2 Η Μηχανή Τούρινγκ ως υπολογιστής συναρτήσεων ακεραίων αριθμών
Εκτός από το να αποδέχεται γλώσσες, μια ΜΤ μπορεί να ιδωθεί και σαν υπολογιστής συναρτήσεων ακεραίων αριθμών. Προς το σκοπό αυτό, κατά σύμβαση παριστάνουμε τους ακέραιους αριθμούς στο μοναδιαίο σύστημα, όπου ο ακέραιος n παριστάνεται ως 1n, δηλαδή σαν μια ακολουθία από n μονάδες. Τα k ορίσματα α1, α2, ..., αk της συνάρτησης παριστάνονται στην ταινία σαν αντίστοιχες ακολουθίες απο μονάδες, χωρισμένες η μία από την άλλη με ένα μηδενικό (0). Επομένως Σ = {0, 1}, αλλά μόνο το 1 χρησιμοποιείται για την παράσταση των ακεραίων, ενώ το 0 χρησιμοποιείται σαν διαχωριστικό. Η ΜΤ τίθεται σε λειτουργία, και αν τερματίζοντας αφήσει στην ταινία τον ακέραιο 1m, τότε λέμε οτι υπολόγισε τη συνάρτηση f (α1, α2, ..., αk) = m.
Ορισμός: Όταν η f (α1, α2, ..., αk) ορίζεται για καθένα από τα k ορίσματά της, τότε ονομάζεται πλήρης αναδρομική συνάρτηση.
Οι πλήρεις αναδρομικές συναρτήσεις αντιστοιχούν στις ΜΤ που τερματίζουν πάντα, για όλες τις συμβολοσειρές ειδόδου-τους, επομένως αντιστοιχούν στις αποφασίσιμες γλώσσες.
Ορισμός: Όταν η f (α1, α2, ..., αk) ορίζεται για μερικά αλλά όχι για όλα τα k ορίσματά της, τότε ονομάζεται μερική αναδρομική συνάρτηση.
Οι μερικές αναδρομικές συναρτήσεις αντιστοιχούν στις ΜΤ που τερματίζουν όταν τους δίνεται μια συμβολοσειρά που ανήκει στη γλώσσα, αλλά που δεν είναι απαραίτητο να τερματίσουν αν τους δοθεί συμβολοσειρά εκτός της γλώσσας. Επομένως αντιστοιχούν στις ημιαποφασίσιμες γλώσσες, και πιο γενικά, στις αναδρομικά απαριθμήσιμες γλώσσες.
Ας συγκριθούν οι παραπάνω ορισμοί με τους ορισμούς της §2.9, όπου ορίσαμε την έννοια “αλγόριθμος”. Μπορούμε λοιπόν τώρα να σχηματίσουμε τις αντιστοιχίες:
| Γλώσσα | Συνάρτηση | Μέθοδος λύσης προβλήματος | |||||||||
| αποφασίσιμη |
|
πλήρης αναδρομική |
|
πλήρης αλγόριθμος |
|
||||||
| ημιαποφασίσιμη | μερική αναδρομική | ημιαλγόριθμος | |||||||||
| αναποφασίσιμη | δεν υπάρχει συνάρτηση | δεν υπάρχει αλγόριθμος | |||||||||
5.5 Ιδιότητες κλειστότητας αποφασίσιμων και αναδρομικά απαριθμήσιμων γλωσσών
Όπως και με τις προηγούμενες περιπτώσεις γλωσσών, θα εξετάσουμε εδώ τί συμβαίνει με τα συμπληρώματα και τις ενώσεις των παραπάνω κατηγοριών γλωσσών.
Θεώρημα 5.5.1: Αν μια γλώσσα L είναι αποφασίσιμη, τότε το συμπλήρωμά της L΄ είναι επίσης αποφασίσιμη γλώσσα.
|
Απόδειξη. Εφόσον η L είναι αποφασίσιμη, θα υπάρχει μια ΜΤ Μ(L) που τερματίζει με όλες τις συμβολοσειρές εισόδου και αποδέχεται την L. Κατασκευάζουμε επομένως την Μ΄ από την Μ έτσι ώστε: όταν η Μ μπαίνει σε τελική κατάσταση δεδομένης μιας εισόδου w, τότε η Μ΄ τερματίζει χωρίς αποδοχή· και αν η Μ τερματίσει χωρίς αποδοχή, τότε η Μ΄ μπαίνει σε τελική κατάσταση αποδεχόμενη την είσοδο. (Βλ. εικόνα 5.5.1)
Εικ. 5.5.1: Κατασκευή της ΜΤ Μ΄ του συμπληρώματος από τη Μ Εφόσον η μία από τις παραπάνω δύο περιπτώσεις οφείλει να συμβεί, η Μ΄ αντιστοιχεί σε πλήρη αλγόριθμο. Καθώς η L(Μ΄) είναι το συμπλήρωμα της L(Μ), έπεται οτι το συμπλήρωμα της L είναι αποφασίσιμη γλώσσα. ▓ |
Θεώρημα 5.5.2: Η ένωση δύο αποφασίσιμων γλωσσών είναι αποφασίσιμη.
|
Απόδειξη. Έστω οι γλώσσες L1 και L2 που είναι αποφασίσιμες, άρα αποδεκτές από τις ΜΤ με πλήρεις αλγορίθμους Μ1 και Μ2. Κατασκευάζουμε τη ΜΤ Μ, η οποία πρώτα προσομοιώνει τη Μ1. Αν η Μ1 αποδεχτεί την είσοδό της, τότε και η Μ αποδέχεται την ίδια είσοδο. Αν η Μ1 την απορρίψει, τότε η Μ προσομοιώνει τη Μ2, και αποδέχεται την είσοδο τότε και μόνο τότε όταν την αποδέχεται και η Μ2. (Βλ. εικόνα 5.5.2.) Εφόσον τόσο η Μ1 όσο και η Μ2 είναι πλήρεις αλγόριθμοι, η Μ εγγυημένα θα τερματίσει και είναι πλήρης αλγόριθμος.
Εικ. 5.5.2: Κατασκευή της Μ από τις Μ1 και Μ2 Από την κατασκευή-της, προφανώς η Μ
αποδέχεται τη γλώσσα L1
|
Πόρισμα 5.5.1: Η τομή δύο αποφασίσιμων γλωσσών είναι αποφασίσιμη.
Απόδειξη. Η απόδειξη έπεται άμεσα από τα θεωρήματα 5.5.1 και 5.5.2.
Θεώρημα 5.5.3: Η ένωση δύο αναδρομικά απαριθμήσιμων γλωσσών είναι αναδρομικά απαριθμήσιμη.
|
Απόδειξη. Ας σημειώσουμε πρώτα οτι η κατασκευή του προηγούμενου θεωρήματος 5.5.2 για τις γλώσσες L1 και L2 δεν θα δουλέψει στην περίπτωση αυτή, γιατί η Μ1 μπορεί να μην τερματίσει. Αντί γι’ αυτό, κατασκευάζουμε την Μ ως μη αιτιοκρατική ΜΤ ώστε να προσομοιώνει παράλληλα τη Μ1 και τη Μ2. Αν είτε η Μ1 είτε η Μ2 τερματίσει με αποδοχή, τότε και η Μ τερματίζει με αποδοχή· αλλιώς, αν καί η Μ1 καί η Μ2 συνεχίσουν επ’ άπειρο, τότε και η Μ συνεχίζει επ’ άπειρο. (Βλ. εικόνα 5.5.3.)
Εικ. 5.5.3: Κατασκευή της Μ από τις Μ1 και Μ2 Από την κατασκευή-της, προφανώς η Μ
αναδρομικά απαριθμεί τη γλώσσα L1
|
Τί μπορούμε να συμπεράνουμε όμως για το συμπλήρωμα μιας αναδρομικά απαριθμήσιμης γλώσσας; Αν και το συμπλήρωμα είναι αναδρομικά απαριθμήσιμο, τότε η γλώσσα ανήκει στην υποκατηγορία των αποφασίσιμων, όπως λέει το ακόλουθο θεώρημα.
Θεώρημα 5.5.4: Αν τόσο η γλώσσα L όσο και το συμπλήρωμά της L΄ είναι αναδρομικά απαριθμήσιμες, τότε η L και η L΄ είναι αποφασίσιμες.
|
Απόδειξη. Έστω οτι οι Μ1 και Μ2 αποδέχονται τις L και L΄ αντίστοιχα. Κατασκευάζουμε την Μ, όπως στην εικόνα 5.5.4, ώστε να προσομοιώνει παράλληλα (μη αιτιοκρατικά) τις Μ1 και Μ2. Η Μ αποδέχεται την είσοδο αν την αποδέχεται η Μ1, και την απορρίπτει αν την αποδέχεται η Μ2. Εφόσον η είσοδος είναι είτε στην L είτε στην L΄, γνωρίζουμε οτι ακριβώς μία από τις Μ1 και Μ2 θα την αποδεχτεί. Έτσι, η Μ θα απαντήσει είτε με αποδοχή είτε με απόρριψη, αλλά ποτέ και με τα δύο αποτελέσματα.
Εικ. 5.5.4: Κατασκευή της Μ από τις Μ1 και Μ2 Εφόσον η Μ είναι πλήρης αλγόριθμος, έπεται οτι η L (φυσικά και το συμπλήρωμά της L΄) είναι αποφασίσιμη. ▓ |
Πόρισμα 5.5.2: Αν η L και η L΄ είναι δύο συμπληρωματικές γλώσσες, τότε:
-
είτε τόσο η L όσο και η L΄ είναι αποφασίσιμη·
-
είτε καμία από τις L και L΄ δεν είναι αναδρομικά απαριθμήσιμη (δηλ. καί οι δύο είναι αναποφασίσιμες)·
-
είτε μία από τις L ή L΄ είναι ημιαποφασίσιμη ενώ η άλλη είναι αναποφασίσιμη.
Θυμίζουμε οτι “ημιαποφασίσιμη” σημαίνει “αναδρομικά απαριθμήσιμη αλλά όχι αποφασίσιμη”, ενώ “αναποφασίσιμη” σημαίνει “όχι αναδρομικά απαριθμήσιμη”.
Από το πόρισμα 5.5.2 προκύπτει μια μέθοδος για να αποδεικνύουμε οτι μια γλώσσα είναι αναποφασίσιμη: αποδεικνύουμε οτι το συμπλήρωμα της γλώσσας δεν είναι αναδρομικά απαριθμήσιμο, επομένως μία των περιπτώσεων 2 ή 3 του πορίσματος πρέπει να ισχύει. Με τον τρόπο αυτό, θα αποδείξουμε την ύπαρξη μιας αναποφασίσιμης γλώσσας στην ακόλουθη υποενότητα.
5.6 Κωδικοποίηση Μηχανών Τούρινγκ και αναποφασίσιμες γλώσσες
5.6.1 Κωδικοποίηση Μηχανών Τούρινγκ
Έστω οτι τίθεται το εξής πρόβλημα: «Μπορούμε άραγε να κατασκευάσουμε μια ΜΤ που να δέχεται στην είσοδό της οποιαδήποτε ΜΤ Μ και οποιαδήποτε συμβολοσειρά w, και να απαντάει “ναι” αν η Μ αποδέχεται την w ; »
Έχουμε λοιπόν εδώ να κάνουμε με μηχανές οι οποίες δέχονται στην είσοδό τους και εξετάζουν άλλες μηχανές. Πριν προχωρήσουμε για να βρούμε την απάντηση στο παραπάνω ερώτημα, θα πρέπει να υποδείξουμε έναν τρόπο με τον οποίο μια ΜΤ μπορεί να κωδικοποιηθεί σε ένα αλφάβητο ώστε να παρουσιαστεί έτσι στην ταινία μιας άλλης ΜΤ (της ζητούμενης στο παραπάνω ερώτημα). Ας δούμε λοιπόν έναν από τους πολλούς (άπειρους, στην πραγματικότητα) τρόπους κωδικοποίησης μιας ΜΤ.
Θα κωδικοποιήσουμε ΜΤ με αλφάβητο Σ = {0, 1}. Όπως είδαμε από το θεώρημα 5.3.3, αρκεί το αλφάβητο Σ = {0, 1} (εξυπακούεται με Γ = {0, 1, ‿}) για να έχουμε μια ΜΤ με πλήρη ικανότητα αποδοχής αναδρομικά απαριθμήσιμης γλώσσας, εφόσον μεγαλύτερα αλφάβητα δεν προσθέτουν κάτι στην ικανότητα της ΜΤ. Έστω λοιπόν η Μ:
Μ = (Q, {0, 1}, {0, 1, ‿}, δ, q1, ‿, {q2})
με Q = {q1, q2, ..., qn}. Δεν χάνεται η γενικότητα αν υποθέσουμε οτι το σύνολο τελικών καταστάσεων {q2} έχει μόνο μία κατάσταση καθώς αν το σύνολο αυτό είναι μεγαλύτερο, μπορούμε πάντα να “οδηγήσουμε” όλες τις τελικές qi σε μία.
Ας μετονομάσουμε τα σύμβολα 0, 1, και ‿, ως Χ1, Χ2, και Χ3, αντίστοιχα. Επίσης, τις κινήσεις Α και Δ της κεφαλής ας τις μετονομάσουμε Κ1 και Κ2 αντίστοιχα. Οπότε τη μετάβαση δ (qi, Xj) = (qk, Xl, Km) μπορούμε να την κωδικοποιήσουμε ως εξής:
| (a) | 0i10j10k10l10m |
Χρησιμοποιούμε δηλαδή έναν αριθμό n μηδενικών για να παραστήσουμε τον αριθμό n, και τα 0 τα διαχωρίζουμε με το 1. Η ΜΤ τώρα μπορεί να κωδικοποιηθεί ως εξής:
111 κώδιξ 1 11 κώδιξ 2 11 ... 11 κώδιξ r 111
όπου καθένα από τα “κώδιξ
i”, 1
![]() i
i
![]() r, είναι της μορφής (a),
παραπάνω. Κάθε μετάβαση της Μ υπάρχει σε ένα από τα “κώδιξ
i”. Φυσικά, επειδή δεν ορίσαμε κάποια σειρά
με την οποία πρέπει να εμφανίζονται οι μεταβάσεις, κάθε ΜΤ έχει πολλές
κωδικοποιήσεις. Μας αρκεί το οτι υπάρχει τουλάχιστον μία κωδικοποίηση
της ΜΤ. Επίσης, κάθε δυαδική συμβολοσειρά μπορεί να είναι κωδικοποίηση για
το πολύ μία ΜΤ, ενώ πολλές δυαδικές συμβολοσειρές (η μεγάλη πλειοψηφία) δεν
αποτελούν κωδικοποιήσεις καμιάς ΜΤ.
r, είναι της μορφής (a),
παραπάνω. Κάθε μετάβαση της Μ υπάρχει σε ένα από τα “κώδιξ
i”. Φυσικά, επειδή δεν ορίσαμε κάποια σειρά
με την οποία πρέπει να εμφανίζονται οι μεταβάσεις, κάθε ΜΤ έχει πολλές
κωδικοποιήσεις. Μας αρκεί το οτι υπάρχει τουλάχιστον μία κωδικοποίηση
της ΜΤ. Επίσης, κάθε δυαδική συμβολοσειρά μπορεί να είναι κωδικοποίηση για
το πολύ μία ΜΤ, ενώ πολλές δυαδικές συμβολοσειρές (η μεγάλη πλειοψηφία) δεν
αποτελούν κωδικοποιήσεις καμιάς ΜΤ.
Την κωδικοποίηση της ΜΤ Μ την τοποθετούμε στην ταινία, ακολουθούμενη αμέσως από τη συμβολοσειρά εισόδου w. Αυτό το ζεύγος συμβολοσειρών το συμβολίζουμε < Μ, w >, και είναι η συμβολοσειρά εισόδου για τη ΜΤ που θα εξετάσει τις ιδιότητες της Μ.
5.6.2 Μια αναποφασίσιμη γλώσσα
Θα κατασκευάσουμε τώρα μια γλώσσα για την οποία δεν θα υπάρχει ΜΤ που να την αποδέχεται. Θα είναι δηλαδή μια αναποφασίσιμη γλώσσα.
Απαριθμούμε όλες τις συμβολοσειρές εισόδου
w
![]() (0 + 1)*
κατά σειρά, π.χ. κατά σειρά αύξουσας αριθμητικής τιμής (εφόσον είναι
δυαδικοί αριθμοί) και τις τοποθετούμε σε μία στήλη, αριστερά του πίνακα που
φαίνεται στην εικόνα 5.6.1. Επομένως η γραμμή i
του πίνακα αντιστοιχεί στην wi.
(0 + 1)*
κατά σειρά, π.χ. κατά σειρά αύξουσας αριθμητικής τιμής (εφόσον είναι
δυαδικοί αριθμοί) και τις τοποθετούμε σε μία στήλη, αριστερά του πίνακα που
φαίνεται στην εικόνα 5.6.1. Επομένως η γραμμή i
του πίνακα αντιστοιχεί στην wi.
Απαριθμούμε επίσης τις ΜΤ μέσω των κωδικοποιήσεών τους με τον ίδιο τρόπο, δηλαδή κατά αύξουσα αριθμητική τιμή, και τις τοποθετούμε σε μία γραμμή πάνω από τον πίνακα. Επομένως η στήλη j του πίνακα αντιστοιχεί στη ΜΤ Μj.
Στη θέση (i, j) του πίνακα βάζουμε το 1 αν η Μj αποδέχεται τη wi, και 0 αν την απορρίπτει.

Εικ. 5.6.1: Διαγωνιοποίηση των Μj και wi
Κατασκευάζουμε τώρα τη γλώσσα Ld χρησιμοποιώντας την κύρια διαγώνιο του παραπάνω πίνακα (κόκκινη στην Εικ. 5.6.1), ως εξής: λέμε οτι η wi ανήκει στην Ld αν και μόνο αν η θέση (i, i) του πίνακα είναι 0, δηλαδή αν η Μi απορρίπτει τη wi.
Θεώρημα 5.6.1: Η γλώσσα Ld είναι αναποφασίσιμη.
|
Απόδειξη. Έστω οτι υπάρχει κάποια Μj που αποδέχεται την Ld, δηλαδή L(Μj) = Ld. Τότε αν η wj είναι στην Ld, τότε η θέση (j, j) του πίνακα πρέπει να είναι 0, που σημαίνει οτι η wj δεν είναι στην L(Μj), αντίθετα με την υπόθεση οτι L(Μj) = Ld. Αν πάλι η wj δεν είναι στην Ld, τότε η θέση (j, j) του πίνακα πρέπει να είναι 1, που σημαίνει οτι η wj είναι στην L(Μj), αλλά αυτό δεν γίνεται γιατί L(Μj) = Ld. Καταλήγουμε επομένως σε άτοπο και στις δύο περιπτώσεις, που σημαίνει οτι δεν υπάρχει Μj που να αποδέχεται την Ld. Άρα η Ld είναι αναποφασίσιμη. ▓ |
Έτσι αποδείξαμε οτι υπάρχει τουλάχιστον μία αναποφασίσιμη γλώσσα. Στη συνέχεια θα γνωρίσουμε κι άλλες, και θα δούμε μάλιστα οτι η πλειοψηφία των γλωσσών είναι αναποφασίσιμες.
5.6.3 Η καθολική γλώσσα και η καθολική ΜΤ
Μπορούμε τώρα να ξαναθεωρήσουμε το πρόβλημα: «Υπάρχει ΜΤ που να δέχεται οποιαδήποτε ΜΤ Μ και συμβολοσειρά w, και να απαντάει “ναι” αν η Μ αποδέχεται την w ; » Εφόσον μάθαμε πώς να κωδικοποιούμε τις ΜΤ, το πρόβλημα αυτό είναι μια γλώσσα. Μπορούμε να διατυπώσουμε συμβολικά αυτή τη γλώσσα ως εξής:
Lu = {< Μ, w >, | η Μ αποδέχεται τη w}
όπου < Μ, w
> είναι η κωδικοποίηση της ΜΤ Μ μαζί με την είσοδό της
w. Την Lu
θα την ονομάσουμε “καθολική γλώσσα” (ο δείκτης u
προέρχεται από το universal =
καθολική), γιατί το αν η συμβολοσειρά < Μ, w
> είναι στην Lu
είναι ισοδύναμο με το ερώτημα του αν μια δεδομένη συμβολοσειρά
w ![]() (0 + 1)*
γίνεται αποδεκτή από μια δεδομένη ΜΤ Μ.
(0 + 1)*
γίνεται αποδεκτή από μια δεδομένη ΜΤ Μ.
Θεώρημα 5.6.2: Η γλώσσα Lu είναι αναδρομικά απαριθμήσιμη.
|
Απόδειξη. Η απόδειξη γίνεται μέσω προσομοίωσης της Μ από μια άλλη ΜΤ Μ΄, που χρησιμοποιεί τρεις ταινίες: η πρώτη ταινία έχει τη συμβολοσειρά < Μ, w > · η δεύτερη ταινία προσομοιώνει την ταινία της Μ· και η τρίτη ταινία αποτυπώνει την εκάστοτε κατάσταση της Μ, με το 0i να συμβολίζει την κατάσταση qi. (Οι λεπτομέρειες της προσομοίωσης δίνονται στο [1].) Είναι εύκολο να δούμε οτι η Μ΄ αποδέχεται τη συμβολοσειρά < Μ, w > αν και μόνο αν η Μ αποδέχεται την w. Επίσης, αν η Μ πέσει σε ατέρμονη ανακύκλωση, το ίδιο θα κάνει και η Μ΄. Τέλος, αν η Μ τερματίσει με το w χωρίς αποδοχή, η Μ΄ θα κάνει το ίδιο με το < Μ, w >.▓ |
Ορισμός: Η καθολική Μηχανή Τούρινγκ (ΜΤu) είναι η ΜΤ που αποδέχεται τη γλώσσα Lu.
Ονομάζουμε την ΜΤu “καθολική” γιατί μπορεί να προσομοιώσει οποιαδήποτε ΜΤ Μ με είσοδο w.
Το ερώτημα όμως τώρα είναι αν η Lu είναι “κάτι παραπάνω”: αν είναι αποφασίσιμη. Μπορούμε να δούμε οτι αυτό δεν ισχύει.
Θεώρημα 5.6.3: Η Lu είναι ημιαποφασίσιμη (επομένως όχι πλήρως αποφασίσιμη)
|
Απόδειξη. Από το θεώρημα 5.6.1 είδαμε οτι η διαγώνια γλώσσα Ld είναι αναποφασίσιμη. Επομένως, από το πόρισμα 5.5.2 έπεται οτι το συμπλήρωμά της, η Ld΄, δεν είναι πλήρως αποφασίσιμη. Ας σημειώσουμε οτι η Ld΄ = {wi | η Μi αποδέχεται τη wi}. Μπορεί να δειχτεί οτι η καθολική γλώσσα Lu ανάγεται στο συμπλήρωμα της διαγώνιας γλώσσας, Ld΄. (Η απόδειξη στο [1].) Εφόσον η Ld΄ είναι όχι πλήρως αποφασίσιμη, έπεται το ίδιο και για την Lu. Και εφόσον η Lu είναι αναδρομικά απαριθμήσιμη (θεώρημα 5.6.2), έπεται οτι είναι ημιαποφασίσιμη. ▓ |
Ας θεωρήσουμε τις γλώσσες:
Lne
= { <M> | L(M)
![]()
![]() }
}
και
Le
= { <M> | L(M) =
![]() }
}
Εύκολα βλέπουμε οτι η Lne είναι το συμπλήρωμα της Le, και αντιστρόφως. Μπορεί να δειχτεί οτι η Lne είναι ημιαποφασίσιμη, ενώ η Le είναι αναποφασίσιμη. (Απόδειξη στο [1], κεφ. 8, παράδειγμα 8.2.) Έχουμε δηλαδή την περίπτωση 3 του πορίσματος 5.5.2.
Ας θεωρήσουμε επίσης τις γλώσσες:
Lr = { <M> | η L(M) είναι αποφασίσιμη }
και
Lnr = { <M> | η L(M) είναι ή ημιαποφασίσιμη ή αναποφασίσιμη }
που επίσης είναι συμπληρώματα η μια της άλλης. (Ας σημειωθεί οτι η Lr δεν είναι η γλώσσα { <Μ> | η Μ τερματίζει με κάθε είσοδο}, αν και περιλαμβάνει αυτή τη γλώσσα. Μια ΜΤ Μ μπορεί να αποδέχεται μια αποφασίσιμη γλώσσα παρόλο που η ίδια η Μ μπορεί να πέφτει σε άπειρη ανακύκλωση όταν της δίνονται κάποιες είσοδοι που δεν ανήκουν στην L(M). Εντούτοις, κάποια άλλη ΜΤ ισοδύναμη με τη Μ πρέπει πάντα να τερματίζει.) Μπορεί να δειχτεί (πλήρης απόδειξη επίσης στο [1], κεφ. 8, παράδειγμα 8.3) οτι τόσο η Lr οσο και η Lnr είναι αναποφασίσιμες. Συνεπώς εδώ έχουμε την περίπτωση 2 του πορίσματος 5.5.2.
Τα παραπάνω παραδείγματα μπορούν να γενικευτούν, ως εξής. Καταρχήν χρειαζόμαστε κάποιους ορισμούς:
Ορισμός: Έστω L ένα σύνολο αναδρομικά απαριθμήσιμων γλωσσών. Τότε το L ονομάζεται ιδιότητα των αναδρομικά απαριθμήσιμων γλωσσών.
Ένα σύνολο L έχει την ιδιότητα L αν το L είναι στοιχείο του L.
Ορισμός: Μια ιδιότητα L ονομάζεται τετριμμένη αν το L είναι είτε το κενό σύνολο, είτε όλες οι αναδρομικά απαριθμήσιμες γλώσσες.
Το παρακάτω ονομάζεται “θεώρημα του Ράις (Rice)”, και αφορά τις μη τετριμμένες ιδιότητες:
Θεώρημα 5.6.4 (του Ράις): Οποιαδήποτε μη τετριμμένη ιδιότητα L των αναδρομικά απαριθμήσιμων γλωσσών είναι είτε ημιαποφασίσιμη, είτε αναποφασίσιμη. (Δηλαδή δεν είναι πλήρως αποφασίσιμη.)
(Πλήρης απόδειξη στο [1].)
Πόρισμα 5.6.1: Οι παρακάτω ιδιότητες των αναδρομικά απαριθμήσιμων γλωσσών δεν είναι πλήρως αποφασίσιμες:
-
το αν μια γλώσσα είναι κενή
-
το αν μια γλώσσα είναι πεπερασμένη
-
το αν μια γλώσσα είναι κανονική
-
το αν μια γλώσσα είναι γλώσσα χωρίς συμφραζόμενα.
Συνεπώς, το θεώρημα του Ράις μας λέει οτι δεν μπορούμε να έχουμε πλήρεις αλγορίθμους για οποιαδήποτε “ενδιαφέρουσα” ιδιότητα των αναδρομικά απαριθμήσιμων γλωσσών.
5.7 Η Θέση των Τσερτς – Τούρινγκ
Η Μηχανή Τούρινγκ προτάθηκε από τον Τούρινγκ το 1936. (Στη δημοσίευσή του, την ονόμασε “μηχανή a”.) Το ίδιο έτος, ο Αλόνζο Τσερτς (Alonzo Church), μετέπειτα επιβλέπων καθηγητής της διδακτορικής διατριβής του Τούρινγκ, πρότεινε το υπολογιστικό μοντέλο που ονομάζεται “λογισμός λάμδα” (λ-calculus). Τρία έτη νωρίτερα, ο Αυστριακός μαθηματικός Κουρτ Γκέντελ (Kurt Gödel) μαζί με το Γάλλο Ζακ Ερμπράν (Jacques Herbrand) όρισαν ένα άλλο υπολογιστικό μοντέλο: τις γενικές αναδρομικές συναρτήσεις.
Τελικά ο Τούρινγκ μαζί με τον Τσερτς απέδειξαν οτι όλα αυτά τα μοντέλα είναι ισοδύναμα, δηλαδή αντιστοιχούν στις αναδρομικά απαριθμήσιμες γλώσσες. Επίσης, άλλα συστήματα που αναπτύχθηκαν στη συνέχεια, όπως τα συστήματα Ποστ (από τον Emil Post), αποδείχτηκαν και αυτά ισοδύναμα. Κάθε άλλη προσπάθεια να οριστεί ένα υπολογιστικό σύστημα κατέληξε στο ίδιο αποτέλεσμα: στις αναδρομικά απαριθμήσιμες γλώσσες.
Έτσι, οι Τσερτς – Τούρινγκ από τις παρατηρήσεις αυτές οδηγήθηκαν στο να διατυπώσουν την ακόλουθη αρχή, ή “θέση”:
| Κάθε “υπολογιζόμενη συνάρτηση” είναι μερικώς αναδρομική, δηλαδή μπορεί να υπολογιστεί από μια Μηχανή Τούρινγκ. |
Με άλλα λόγια, η θέση των Τσερτς – Τούρινγκ ισχυρίζεται οτι δεν υπάρχει πιο ισχυρό υπολογιστικό σύστημα από τη Μηχανή Τούριγκ. Η αιτιολόγηση σήμερα είναι οτι αν υπήρχε, θα έπρεπε να το είχαμε ανακαλύψει.
Η θέση αυτή είναι άτυπη, δηλαδή δεν μπορεί να αποδειχτεί σαν θεώρημα, εφόσον η έννοια “υπολογίσιμη συνάρτηση” δεν μπορεί να οριστεί με αυστηρό, τυπικό τρόπο. Ο Γκέντελ ήταν της άποψης οτι η θέση αυτή πρέπει να εκληφθεί απλά σαν ορισμός της έννοιας “υπολογίσιμη συνάρτηση”.
6. Η ιεραρχία του Τσόμσκι
Ορίσαμε, μέχρι το σημείο αυτό, ορισμένες μηχανές (αυτόματα), γραμματικές, και γλώσσες, αποδεικνύοντας κάποιες σχέσεις όπως και ισοδυναμίες μεταξύ μηχανών, γραμματικών, και γλωσσών. Στην παρούσα ενότητα θα κάνουμε τις σχέσεις (και ισοδυναμίες) μεταξύ μηχανών, γραμματικών, και γλωσσών πλήρεις, διαμορφώνοντας έτσι αυτό που ονομάζεται “ιεραρχία του Τσόμσκι”*.
Ας τοποθετήσουμε σε έναν πίνακα τις κατηγορίες των μηχανών, γραμματικών, και γλωσσών που έχουμε εξετάσει μέχρι στιγμής.
| Μηχανές (Αυτόματα) | Γραμματικές | Γλώσσες |
| Πεπερασμένα Αυτόματα | ? | Κανονικές Γλώσσες |
| Αυτόματα Στοίβας | Γραμματικές Χωρίς Συμφραζόμενα | Γλώσσες Χωρίς Συμφραζόμενα |
| ? | ? | ? |
| Μηχανές Τούρινγκ | ? | Αναδρομικά Απαριθμήσιμες Γλώσσες |
Πίνακας 6.1: Σχέσεις μηχανών/αυτομάτων, γραμματικών, και γλωσσών που έχουμε εξετάσει μέχρι στιγμής
Στον Πίνακα 6.1 οι μηχανές, γραμματικές, και γλώσσες που βρίσκονται στην ίδια σειρά αντιστοιχούν η μία με την άλλη. Επίσης, όσο προχωρούμε από πάνω προς τα κάτω στον πίνακα, οι μηχανές, γραμματικές, και γλώσσες, γίνονται ισχυρότερες. Παρατηρούμε όμως οτι η αντιστοιχία είναι πλήρης μόνο σε μία σειρά, τη δεύτερη, ενώ υπάρχουν αρκετές θέσεις με ερωτηματικά. Υπάρχει μάλιστα μία ολόκληρη σειρά με ερωτηματικά, μεταξύ Αυτομάτων Στοίβας και Μηχανών Τούρινγκ. Σκοπός-μας τώρα είναι να συμπληρώσουμε τον Πίνακα 6.1 με συγκεκριμένες μηχανές, γραμματικές, και γλώσσες, ώστε η αντιστοιχία να γίνει πλήρης. Θα δώσουμε μάλιστα από τώρα τις ονομασίες των κελιών του πίνακα που λείπουν (βλ. Πίνακα 6.2), και θα ορίσουμε τις έννοιες αυτές στη συνέχεια.
| Μηχανές (Αυτόματα) | Γραμματικές | Γλώσσες |
| Πεπερασμένα Αυτόματα | Κανονικές Γραμματικές | Κανονικές Γλώσσες |
| Αυτόματα Στοίβας | Γραμματικές Χωρίς Συμφραζόμενα | Γλώσσες Χωρίς Συμφραζόμενα |
| Γραμμικώς Φραγμένα Αυτόματα | Γραμματικές Με Συμφραζόμενα | Γλώσσες Με Συμφραζόμενα |
| Μηχανές Τούρινγκ | Μη Περιορισμένες Γραμματικές | Αναδρομικά Απαριθμήσιμες Γλώσσες |
Πίνακας 6.2: Σχέσεις μηχανών/αυτομάτων, γραμματικών, και γλωσσών, όπως θα συμπληρωθούν στη συνέχεια
Μάλιστα, στη 2η και 4η σειρά του πίνακα έχουμε δημιουργήσει υποκατηγορίες. Μπορούμε έτσι να κάνουμε λίγο πιο πολύπλοκο τον προηγούμενο πίνακα:
| Μηχανές (Αυτόματα) | Γραμματικές | Γλώσσες | ||||||
| Πεπερασμένα Αυτόματα | Κανονικές Γραμματικές | Κανονικές Γλώσσες | ||||||
Αυτόματα Στοίβας
|
Γραμματικές Χωρίς Συμφραζόμενα
|
Γλώσσες Χωρίς Συμφραζόμενα
|
||||||
| Γραμμικώς Φραγμένα Αυτόματα | Γραμματικές Με Συμφραζόμενα | Γλώσσες Με Συμφραζόμενα | ||||||
Μηχανές Τούρινγκ
|
Μη Περιορισμένες Γραμματικές |
Αναδρομικά Απαριθμήσιμες Γλώσσες
|
Πίνακας 6.3: Ο Πίνακας 6.2 με την τέταρτη σειρά πιο αναλυτικά
Τις “Γραμματικές LR(k)” και τις “Σαφείς (μη διφορούμενες) Γλώσσες” δεν θα τις συζητήσουμε περαιτέρω, καθώς είναι χρήσιμες στη θεωρία μεταγλωττιστών (compilers), και συνεπώς εκτός του εύρους του παρόντος μαθήματος. Θα θυμίσουμε μόνο οτι, όπως έχουμε ήδη αναφέρει, για πρακτικούς λόγους, όλες οι γλώσσες προγραμματισμού είναι σαφείς (μη διφορούμενες), επομένως το συντακτικό-τους περιγράφεται από “Γραμματικές LR(k)”.*
Βεβαίως έχουμε δείξει οτι υπάρχουν και οι αναποφασίσιμες γλώσσες, για τις οποίες είδαμε οτι δεν υπάρχουν αντίστοιχες μηχανές (ή γραμματικές). Δείξαμε δηλαδή (θεώρημα 5.6.1), με τη μέθοδο της διαγωνιοποίησης, οτι υπάρχουν γλώσσες που δεν υπολογίζονται. Αυτές δεν περιλαμβάνονται στον Πίνακα 6.3.
6.1 Κανονικές Γραμματικές
Έστω οτι θέτουμε τους ακόλουθους περιορισμύς σε μια γραμματική:
Ορισμός: όταν όλοι οι κανόνες μιας γραμματικής είναι είτε της μορφής Α → xB, είτε της μορφής Α → x, όπου τα Α και Β είναι μεταβλητές και το x είναι μια (ίσως κενή) συμβολοσειρά τερματικών συμβόλων, τότε η γραμματική ονομάζεται δεξιά γραμμική.
Ορισμός: όταν όλοι οι κανόνες μιας γραμματικής είναι είτε της μορφής Α → Bx, είτε της μορφής Α → x, όπου τα Α και Β είναι μεταβλητές και το x είναι μια (ίσως κενή) συμβολοσειρά τερματικών συμβόλων, τότε η γραμματική ονομάζεται αριστερά γραμμική.
Ορισμός: μια γραμματική που είναι είτε δεξιά γραμμική είτε αριστερά γραμμική ονομάζεται κανονική γραμματική.
Παράδειγμα: Ας θεωρήσουμε την κανονική έκφραση (Κ.Ε.): a(ba)*. Αυτή η Κ.Ε. παράγεται από την ακόλουθη δεξιά γραμμική γραμματική:
-
S → aA
-
A → baA | ε
Παράγεται όμως επίσης από την ακόλουθη αριστερά γραμμική γραμματική:
-
S → Sba | a
Συνεπώς η γραμματική που την παράγει είναι κανονική.
Θεώρημα 6.1: Μια γλώσσα L έχει κανονική γραμματική τότε και μόνο τότε όταν η L γίνεται αποδεκτή από ένα πεπερασμένο αυτόματο.
Η απόδειξη, που είναι κατασκευαστική αλλά μακροσκελής, δίνεται στο [1].
Το θεώρημα 6.1 μας λέει οτι γλώσσες με κανονικές γραμματικές είναι οι κανονικές γλώσσες (ή κανονικά σύνολα), δηλαδή αυτές των πεπερασμένων αυτομάτων, συμπληρώνοντας έτσι τη σειρά 1 του Πίνακα 6.3.
6.2 Γραμματικές Με Συμφραζόμενα
Στις
γραμματικές χωρίς συμφραζόμενα (ΓΧΣ)
είδαμε οτι οι κανόνες είναι της μορφής Α → β, όπου το Α είναι
μεταβλητή, και το β είναι συμβολοσειρά από το (V
![]() T)*,
δηλαδή οποιαδήποτε ακολουθία (πιθανώς κενή) μεταβλητών ή τερματικών
συμβόλων. Ας υποθέσουμε τώρα οτι το αριστερό μέλος ενός κανόνα δεν είναι
υποχρεωτικά μόνο μία μεταβλητή, αλλά οποιαδήποτε συμβολοσειρά α
από το (V
T)*,
δηλαδή οποιαδήποτε ακολουθία (πιθανώς κενή) μεταβλητών ή τερματικών
συμβόλων. Ας υποθέσουμε τώρα οτι το αριστερό μέλος ενός κανόνα δεν είναι
υποχρεωτικά μόνο μία μεταβλητή, αλλά οποιαδήποτε συμβολοσειρά α
από το (V
![]() T)*,
δηλαδή ο κανόνας είναι α → β, αλλά το μήκος του β
να είναι μεγαλύτερο ή ίσο του μήκους του α. Τότε έχουμε μια
“γραμματική με συμφραζόμενα”.
T)*,
δηλαδή ο κανόνας είναι α → β, αλλά το μήκος του β
να είναι μεγαλύτερο ή ίσο του μήκους του α. Τότε έχουμε μια
“γραμματική με συμφραζόμενα”.
Ορισμός:
Μια γραμματική με συμφραζόμενα
(ΓΜΣ) είναι μια τετράδα G = (V, T, P, S),
όπως και σε μια ΓΧΣ,
με τη διαφορά οτι στους κανόνες α → β του Ρ τα α, β
![]() (V
(V
![]() T)*,
και ισχύει οτι | α |
T)*,
και ισχύει οτι | α |
![]() |
β |.
|
β |.
Είναι προφανές οτι εφόσον | α |
![]() |
β |, μια ΓΜΣ δεν μπορεί να παραγάγει την κενή συμβολοσειρά ε.
|
β |, μια ΓΜΣ δεν μπορεί να παραγάγει την κενή συμβολοσειρά ε.
Ορισμός: Η γλώσσα που παράγεται από μια ΓΜΣ ονομάζεται γλώσσα με συμφραζόμενα.
Επομένως οι γλώσσες με συμφραζόμενα
δεν περιλαμβάνουν το ε. Αν η γλώσσα είναι κατά τα άλλα γλώσσα με
συμφραζόμενα, και περιλαμβάνει το ε, τότε μπορούμε να
τροποποιήσουμε τον ορισμό των ΓΜΣ ώστε να επιτρέπει έναν επιπλέον
κανόνα, τον S → ε, τον μοναδικό που να
παραβιάζει τη συνθήκη | α |
![]() |
β |.
|
β |.
6.3 Γραμμικώς Φραγμένα Αυτόματα
Υπάρχει ένας περιορισμός των Μηχανών Τούρινγκ, μέσω του οποίου το αυτόματο που προκύπτει έχει μικρότερη υπολογιστική ικανότητα από τη ΜΤ. Ο περιορισμός είναι ο εξής:
Ορισμός: Ένα γραμμικώς φραγμένο αυτόματο (ΓΦΑ) είναι μια ΜΤ με τις ακόλουθες δύο συνθήκες:
-
Το αλφάβητο εισόδου περιλαμβάνει δύο ειδικά σύμβολα, τα # και $, που ονομάζονται αριστερό και δεξιό ακραίο σύμβολο, αντιστοίχως.
-
Το ΓΦΑ δεν μπορεί να κάνει κινήσεις αριστερά από το # στην ταινία, ούτε δεξιά από το $ στην ταινία, ούτε επιτρέπεται να αντικαταστήσει τα # ή $ με άλλα σύμβολα.
Συνεπώς το ΓΦΑ είναι μια ΜΤ της οποίας η ταινία δεν είναι απεριόριστη, αλλά η είσοδός της περιορίζεται μεταξύ των δύο ακραίων συμβόλων. Αποδεικνύεται οτι όταν το μήκος της περιορισμένης αυτής ταινίας είναι γραμμική συνάρτηση του μήκους της εισόδου, τότε το αυτόματο έχει την ισχύ του ΓΦΑ, εξ ου και το “γραμμικώς φραγμένο” στην ονομασία του ΓΦΑ.
Ποια είναι όμως η ισχύς του ΓΦΑ; Αυτό μας το δίνει το παρακάτω θεώρημα.
Θεώρημα 6.2: Η γλώσσα L παράγεται από μια ΓΜΣ τότε και μόνο τότε όταν γίνεται αποδεκτή από ένα ΓΦΑ.
Απόδειξη, στο [1].
Έχουμε έτσι την ισοδυναμία αυτομάτων, γραμματικών, και γλωσσών στην 3η σειρά των Πινάκων 6.2 και 6.3.
6.4 Μη Περιορισμένες Γραμματικές
Ως τώρα, όποτε ορίσαμε μια γραμματική, θέσαμε περιορισμούς στη μορφή των κανόνων-της. Αν αφαιρέσουμε κάθε περιορισμό τότε παίρνουμε μια “μη περιορισμένη γραμματική”:
Ορισμός: Μια μη περιορισμένη
γραμματική (ΜΠΓ)
είναι μια τετράδα G = (V, T, P, S), όπως και
σε μια ΓΧΣ, με τη
διαφορά οτι στους κανόνες α → β του Ρ τα α, β
![]() (V
(V
![]() T)*,
και α
T)*,
και α
![]() ε.
ε.
Οι μη περιορισμένες γραμματικές είναι οι γραμματικές με τη μεγαλύτερη παραγωγική ικανότητα σε γλώσσες, καθώς αποδεικνύεται το ακόλουθο αποτέλεσμα:
Θεώρημα 6.3: Η γλώσσα L παράγεται από μια ΜΠΓ τότε και μόνο τότε όταν η L είναι αναδρομικά απαριθμήσιμη.
Απόδειξη, στο [1].
Συνεπώς, εφόσον οι αναδρομικά απαριθμήσιμες γλώσσες γίνονται αποδεκτές από τις Μηχανές Τούρινγκ, έχουμε την ισοδυναμία αυτομάτων, γραμματικών, και γλωσσών στην 4η σειρά των Πινάκων 6.2 και 6.3.
6.5 Η ιεραρχία του Τσόμσκι
Ποια είναι όμως η “κατακόρυφη” σχέση μεταξύ αυτομάτων, γραμματικών, και γλωσσών στους Πίνακες 6.2 και 6.3; Αποδεικνύεται το ακόλουθο σύνθετο αποτέλεσμα:
Θεώρημα 6.4 (“Ιεραρχία του Τσόμσκι”):
-
Οι κανονικές γλώσσες είναι γνήσιο υποσύνολο των γλωσσών χωρίς συμφραζόμενα.
-
Οι γλώσσες χωρίς συμφραζόμενα είναι γνήσιο υποσύνολο των γλωσσών με συμφραζόμενα.
-
Οι γλώσσες με συμφραζόμενα είναι γνήσιο υποσύνολο των αποφασίσιμων γλωσσών.
-
Οι αποφασίσιμες γλώσσες είναι γνήσιο υποσύνολο των ημιαποφασίσιμων γλωσσών.
Τέλος, έχουμε ήδη αποδείξει οτι οι ημιαποφασίσιμες γλώσσες είναι γνήσιο υποσύνολο των αναποφασίσιμων γλωσσών, για τις οποίες όμως δεν υπάρχει αυτόματο που να τις αποδέχεται (έστω και καταφατικώς).
Υπόψη οτι μερικές φορές στη βιβλιογραφία χρησιμοποιείται και η παρακάτω ορολογία:
| κανονικές γλώσσες | γλώσσες Τύπου 3 |
| γλώσσες χωρίς συμφραζόμενα | γλώσσες Τύπου 2 |
| γλώσσες με συμφραζόμενα | γλώσσες Τύπου 1 |
| μη περιορισμένες γλώσσες | γλώσσες Τύπου 0, ή: γλώσσες δομής φράσης |
Σημειώσεις: (Με κλικ στο ^ επανέρχεστε στο σημείο του κειμένου όπου υπάρχει η αναφορά στην παρούσα υποσημείωση)
^ Τα σημεία, ευθείες, κλπ., λέμε οτι ανήκουν στην “οντολογία” της γεωμετρίας, δηλαδή στο σύνολο εννοιών με τις οποίες ασχολείται η γεωμετρία. Αντίστοιχα, τα σύμβολα (όπως και οι συμβολοσειρές, τα αλφάβητα, οι γλώσσες, κλπ., που ορίζονται αμέσως παρακάτω στο κυρίως κείμενο) αποτελούν την οντολογία της παρούσας θεωρίας.
^ Ας σημειωθεί οτι όροι όπως “πληθάριθμος” (αγγλ.: cardinality) ανήκουν στη θεωρία συνόλων, επομένως στα προαπαιτούμενα του μαθήματος. Το ίδιο ισχύει και για κάθε άλλο όρο του οποίου ο ορισμός δεν δίνεται στο παρόν κείμενο, όπως: “συνάρτηση”, “σχέση”, “ένωση”, “τομή”, κλπ.
^ Δεν χρειάζεται να επαναλαμβάνουμε το «και μόνο αν» από εδώ και μπρος στους ορισμούς. Θυμίζουμε οτι στα μαθηματικά κάθε ορισμός γίνεται αντιληπτός πάντοτε σαν «αν και μόνο αν».
^ Το όνομα αυτό προφέρεται “κλίνι” ή “κλιν” από πρακτικά όλους τους ομιλούντες την αγγλική. Ο ίδιος ο Stephen Cole Kleene όμως πρόφερε το όνομά του ως “κλέινι” (ίδια πηγή), και αυτή η προφορά έχει επικρατήσει (παραδόξως) στην ελληνική απόδοση.
^ Παρόλο που η εποπτική παράσταση των αυτομάτων δεν είναι υποχρεωτική από μαθηματική άποψη, εντούτοις είναι πρακτικά απαραίτητη για την κατανόηση της λειτουργίας ενός αυτομάτου.
^ Ο λόγος που τα δέντρα απεικονίζονται “ανάποδα” (από πάνω προς τα κάτω) είναι προφανής: η ανάγνωση γίνεται από πάνω προς τα κάτω, και το φυσικό σημείο εκκίνησης για την ανάγνωση του διαγράμματος ενός δέντρου είναι η ρίζα-του.
^ Από εδώ και στο εξής θα μιλάμε για ένα ΠΑ που “εικονίζεται” σε ένα διάγραμμα που δείχνει έναν γράφο, με τον οποίο θα υποθέτουμε οτι το αλφάβητο εισόδου αποτελείται μόνο από τα σύμβολα που φαίνονται στον γράφο, και η συνάρτηση μετάβασης δ είναι ακριβώς εκείνη που καθορίζεται από τις ακμές του γράφου.
^ Η έννοια της ισοδυναμίας μεταξύ ΠΑ θα εξεταστεί σε επόμενη ενότητα. Προς το παρόν, άτυπα, μπορούμε να πούμε οτι δύο ΠΑ είναι ισοδύναμα όταν κάνουν αποδεκτό το ίδιο σύνολο συμβολοσειρών (ή “αναγνωρίζουν την ίδια γλώσσα” — όρος που δίνεται αμέσως παρακάτω στο κυρίως κείμενο).
^ Όταν ένα ΜΠΑ υλοποιείται σε υπολογιστή, και ο σκοπός είναι να αποφασίσει την αποδοχή ή απόρριψη μιας δεδομένης συμβολοσειράς εισόδου, τότε — αντίθετα με την αναφερθείσα “ερμηνεία πολλαπλών κόσμων” — πρέπει να είναι παρών ένας μηχανισμός στο πρόγραμμα ώστε αν κάποια από τις παράλληλες διαδικασίες, που καθεμία υλοποιεί ένα αντίγραφο του ΜΠΑ, τερματίσει, να πληροφορήσει τις υπόλοιπες διαδικασίες ώστε να σταματήσουν να τρέχουν. Αυτό είναι απαραίτητο γιατί στους υπολογιστές είναι επιθυμητό τα προγράμματα να σταματούν να τρέχουν όσο το δυνατόν γρηγορότερα. Αλλά αν ο σκοπός είναι να απαριθμηθούν μερικές από τις αποδεκτές συμβολοσειρές της γλώσσας που αναγνωρίζει το αυτόματο, τότε αυτό το σήμα (για να σταματήσουν οι άλλες παράλληλες διαδικασίες) είναι περιττό.
^ Από τον Νόουμ Τσόμσκι (Noam Chomsky), τον Αμερικανό γλωσσολόγο, νοολόγο, και πολιτικό ακτιβιστή, που θεωρείται “πατέρας της σύγχρονης γλωσσολογίας”, ο οποίος όρισε τις κλάσεις ισοδυναμίας των γλωσσών που περιγράφονται στην ενότητα αυτή ως πιθανά μοντέλα για φυσικές γλώσσες.
^ Προσοχή: άλλο η γραμματική (συντακτικό) μιας γλώσσας προγραμματισμού, και άλλο το τί μπορεί να υπολογίσει το πρόγραμμα που ορίζεται από μια τέτοια γραμματική. Το πρόγραμμα, φυσικά, έχει πάντα την ισχύ της Μηχανής Τούρινγκ.
Βιβλιογραφία
-
Hopcroft, John E., and Jeffrey D. Ullman (1979). Introduction to Automata Theory, Languages, and Computation. Addison Wesley, Reading, Massachusetts.
-
Papadimitriou, Christos E. (1994). Computational Complexity. Addison Wesley, Reading, Massachusetts.
-
Sipser, Michael (2013). Introduction to the Theory of Computation (3rd ed.). Cengage Learning, Boston, Massachusetts.
Πίσω στη γενική σελίδα του Διαδικτυακού Επιστημονικού Πανεπιστημίου