Δ.Ε.Π. : Μάθημα Ε2 : Ιστορία και Εξέλιξη της Επιστήμης, Μέρος 3ο: Εικοστός Αιώνας

Προς το τέλος του 19^ου αιώνα όλα έδειχναν ήρεμα στον τομέα της επιστήμης. Φαινόταν σαν να είχαν ήδη γίνει οι μεγαλύτερες ανακαλύψεις, και να είχαν παγιωθεί οι πιο σημαντικές ιδέες. Ίσως ο επόμενος αιώνας να είχε να συνεισφέρει κάποια πράγματα, τα οποία όμως θα ήσαν απλές υποσημειώσεις στα ήδη γνωστά — έτσι σκέφτονταν πολλοί επιστήμονες. Αυτή την άποψη άλλωστε λέγεται (χωρίς βεβαιωμένη πηγή όμως) οτι εξέφρασε ο Ουΐλλιαμ Τόμπσον, πιο γνωστός ως Λόρδος Κέλβιν, περί το 1900: «Δεν υπάρχει τίποτε το νέο για ν’ ανακαλυφθεί πλέον στη φυσική. Το μόνο που απομένει είναι απλώς όλο και περισσότερο ακριβείς μετρήσεις.» Υπήρχαν βέβαια μερικά ανοιχτά ερωτήματα, όπως το ποιο είναι το μέσον μέσω του οποίου διαδίδεται το φως στο κενό (για το οποίο, όπως είδαμε στο εδάφιο περί Faraday και Maxwell, είχε υποτεθεί οτι είναι “ο αιθέρας”)· ή το πώς μπορεί ο Ήλιος να λάμπει επί τόσο χρόνο, εφόσον, αν αποτελείται από άνθρακα — που ήταν η τότε γνωστή ουσία που χρησιμοποιούσαν στην καύση — θα έπρεπε να έχει εξαντληθεί και σβήσει προ πολλού. Τα ερωτήματα αυτά όμως ακούγονταν σαν “λεπτομέρειες”. Κανείς δεν μπορούσε να φανταστεί την επανάσταση που θα έφερναν στο χώρο της φυσικής οι λεπτομέρειες αυτές, και το τί θα επακολουθούσε.

Η αυγή της θεωρίας των κβάντα

Ο Πλανκ έκανε επομένως το “επιστημονικά σωστό”: εφόσον τα δεδομένα έδειχναν άλλη συμπεριφορά από αυτήν που προέβλεπε η θεωρία, άρα ήταν η θεωρία που έπρεπε ν’ αλλάξει, και όχι ν’ αγνοηθούν τα δεδομένα. Επειδή όμως δεν είχαν ακόμη συσσωρευθεί οι παρατηρήσεις που να αντίκεινται στην κλασική ηλεκτρομαγνητική θεωρία, ο Πλανκ εισήγαγε τη σταθερά h “με μισή καρδιά”, χωρίς να φαντάζεται το θεμελιώδη ρόλο που θα έπαιζε στη φυσική του 20^ού αιώνα. Ο λόγος για τον οποίο η ακτινοβολία του μέλανος σώματος εκπέμπεται μόνο κατά πολλαπλάσια της σταθεράς h είναι — όπως έγινε κατανοητό πολλά χρόνια αργότερα — οτι η ακτινοβολία προκύπτει καθώς ένα ηλεκτρόνιο που βρίσκεται σε μια στοιβάδα ενός ατόμου “πέφτει” σε μια στοιβάδα χαμηλότερης ενέργειας, και κατά την “πτώση” αυτή αποβάλλεται ένα φωτόνιο, που είναι αυτό που παρατηρούμε σαν “ηλεκτρομαγνητική ακτινοβολία”. Επειδή η “πτώση” αφορά σε διακριτές τιμές (από μια ανώτερη στοιβάδα σε μια κατώτερη), γιαυτό και η συχνότητα της ακτινοβολίας έχει συγκεκριμένες, διακριτές τιμές. Η σταθερά h ονομάστηκε αργότερα “σταθερά του Πλανκ”, και είναι μία από τις θεμελιώδεις σταθερές του σύμπαντός μας. Δηλαδή, αν η h είχε ελαφρώς διαφορετική τιμή, οι ιδιότητες του σύμπαντος θα ήσαν πολύ διαφορετικές (και κατά πάσαν πιθανότητα δεν θα υπήρχαμε). Ο Πλανκ έκανε την πιο σημαντική δημοσίευσή του το 1901, κ’ έτσι, με την αυγή του 20^ού αιώνα, ξεκίνησε και η πρώτη επανάσταση στο χώρο της φυσικής, χωρίς να το υποπτεύεται ακόμη τότε κανένας.

Λίγα χρόνια αργότερα, το 1905, ήρθε μια δεύτερη δημοσίευση από το νεαρό φυσικό Άλμπερτ Αϊνστάιν, για να επιβεβαιώσει το οτι το φως έχει διακριτές τιμές και άρα σωματιδιακή φύση, σύμφωνα με το Νιούτον και αντίθετα με την μέχρι τότε παραδεκτή κυματική φύση του φωτός. Ο Αϊνστάιν δημοσίευσε τις παρατηρήσεις-του πάνω στο “φωτοηλεκτρικό φαινόμενο”. Το “φαινόμενο Αϊνστάιν” όμως έμελλε να χαράξει μια πολύ πιο βαθιά τομή στην κλασική φυσική μέσω της “θεωρίας της σχετικότητας”, που συζητείται αμέσως στη συνέχεια.

Αντί να πούμε οτι η ηλεκτρομαγνητική ακτινοβολία “δεν είναι συνεχής”, λέμε οτι είναι “κβαντισμένη”, και οτι τα διακριτά “πακέτα” μέσω των οποίων επέμπεται από τα άτομα ενος υλικού λέγονται “κβάντα φωτός” (ή “φωτόνια”, οπως ονομάστηκαν αργότερα). Πιο γενικά, κατά τον 20^ό αιώνα διαπιστώθηκε οτι και άλλες φυσικές ποσότητες ειναι κβαντισμένες (διακριτές), και όχι συνεχείς. Έτσι, η νέα φυσική ονομάστηκε “κβαντική φυσική”.

Albert Einstein (Άλμπερτ Αϊνστάιν, 1879 – 1955), και η θεωρία της σχετικότητας

Κατά το 1887, οι Αμερικανοί φυσικοί Albert Michelson και Edward Morley έκαναν ένα πείραμα προκειμένου να μετρήσουν την ταχύτητα της Γης διαμέσου του αιθέρα. Η ιδέα των Michelson–Morley ήταν η εξής: αν η Γη κινείται μέσα στον αιθέρα καθώς διαγράφει την ετήσια περιφορά-της γύρω από τον Ήλιο, θα πρέπει να δέχεται έναν “αιθέριο άνεμο” (όπως δηλαδή όταν κινούμαστε μέσα στον αέρα και δεχόμαστε τον άνεμο κατά πρόσωπο, ή από το πλάι, κλπ). Η κίνηση της Γης μέσα στον αιθέρα θα πρέπει να είναι μετρήσιμη στέλνοντας ακτίνες φωτός προς διάφορες διευθύνσεις: καθώς το φως θα στέλνεται από τη Γη προς μία διεύθυνση π.χ. ενάντια στον αιθέριο άνεμο, θα πρέπει να έχει ταχύτητα μικρότερη απ’ ότι όταν στέλνεται προς διεύθυνση ίδια με τον αιθέριο άνεμο. (Όπως π.χ. ένας κολυμβητής σε ποτάμι, που έχει μικρότερη ταχύτητα όταν κολυμπάει αντίθετα με το ρεύμα παρά όταν κολυμπάει μαζί με το ρεύμα.) Οι Michelson–Morley δεν ήξεραν βέβαια “προς τα πού φυσάει” ο υποτιθέμενος αιθέριος άνεμος, περίμεναν όμως να μετρήσουν κάποια διαφορά στην ταχύτητα του φωτός μεταξύ των διαφόρων διευθύνσεων.

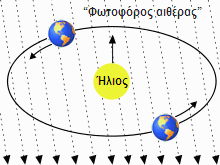
Καμία όμως διαφορά στην ταχύτητα του φωτός δεν έγινε δυνατό να μετρηθεί. Ούτε οι Michelson–Morley, ούτε κανείς άλλος που επανέλαβε το πείραμά τους, με όλο και πιο ακριβείς πειραματικές εγκαταστάσεις, μπόρεσε να παρατηρήσει κάποια διαφορά στην ταχύτητα του φωτός. Ας πούμε οτι η Γη είναι ένας δρομέας, και οτι η ακτίνα φωτός αντιστοιχεί σε μια πέτρα που ο δρομέας αυτός ρίχνει καθώς τρέχει, ενώ η ατμόσφαιρα αντιστοιχεί στον αιθέρα. Ήταν λοιπόν σαν η πέτρα να είχε πάντα την ίδια ταχύτητα ως προς το έδαφος, ανεξάρτητα από το πόσο γρήγορα έτρεχε ο δρομέας ή πόσο δυνατά φυσούσε ο άνεμος, και ανεξάρτητα από το αν ο δρομέας έριχνε την πέτρα προς τα μπρος ή προς τα πίσω. Το συμπέρασμα που βγήκε από το αποτυχημένο πείραμα των Michelson–Morley δεν ήταν οτι ο αιθέρας δεν υπάρχει, αλλά οτι η κίνηση της Γης μέσα στον αιθέρα είναι τόσο μικρή που δεν είναι μετρήσιμη· δηλαδή οτι η Γη είναι πρακτικά ακίνητη μέσα στον αιθέρα. Αυτό το συμπέρασμα από μόνο-του είναι παράλογο, αφού αν η Γη είναι ακίνητη σε σχέση με τον αιθέρα, τότε θα πρέπει να κινείται ο Ήλιος και όλα τα άλλα ουράνια σώματα, αφού εκείνα κινούνται ως προς τη Γη. Όμως γιατί να έχει η Γη μια τέτοια ειδική μεταχείριση; Γιατί να είναι μόνο η Γη ακίνητη σε σχέση με τον αιθέρα, και όλα τα άλλα ουράνια σώματα να κινούνται;

Ο Αϊνστάιν στην πραγματικότητα δεν επηρεάστηκε από το πείραμα των Michelson–Morley, γιατί απλά δεν το είχε υπόψη-του. Έφτασε μέσω δικών-του συνειρμών (“πειραμάτων σκέψης”, όπως ονομάστηκαν από τότε) στην υπόθεση οτι η ταχύτητα του φωτός είναι πάντα σταθερή, ανεξάρτητη από την ταχύτητα της πηγής που το παράγει και το εκπέμπει. Όταν όμως αργότερα έγινε γνωστή η θεωρία της σχετικότητας, το πείραμα των Michelson–Morley θεωρήθηκε οτι παρείχε μια επιβεβαίωση της θεωρίας, όπως επίσης και οτι έδινε μια ένδειξη του οτι ο “φωτοφόρος αιθέρας” δεν υπάρχει.

Το 1905 έλαβε το διδακτορικό-του τίτλο από το Πανεπιστήμιο της Ζυρίχης, και το ίδιο έτος δημοσίευσε τέσσερις κοσμοϊστορικές δημοσιεύσεις στο γερμανικό περιοδικό Annalen der Physik (Χρονικά της Φυσικής):

Λόγω των παραπάνω, το 1905 ονομάστηκε “έτος θαυμάτων” (“annus mirabilis”) από την επιστημονική κοινότητα.

Ειδική θεωρία της σχετικότητας

Όπως προαναφέρθηκε, η ειδική θεωρία της σχετικότητας ξεκινάει από το αξίωμα οτι η ταχύτητα του φωτός στο κενό είναι σταθερή, και ανεξάρτητη από την ταχύτητα της πηγής που την εκπέμπει. Είναι δηλαδή σαν, όσο γρήγορα και να τρέχει ο δρομέας που πετάει την πέτρα (ακτίνα φωτός), η πέτρα να έχει πάντα σταθερή ταχύτητα ως προς οποιονδήποτε παρατηρητή: τόσο ως προς το δρομέα, όσο και ως προς έναν παρατηρητή που μένει στο έδαφος. Αυτό είναι τελείως ενάντιο στην ανθρώπινη εμπειρία: όταν ο δρομέας τρέχει με ταχύτητα v₁ ως προς το έδαφος, και πετάει μια πέτρα με ταχύτητα v₂ ως προς τον εαυτό-του, τότε αναμένουμε η πέτρα να έχει ταχύτητα v=v₁+v₂ ως προς το έδαφος, δηλαδή το άθροισμα των ταχυτήτων. Πιο παραστατικά, η μετωπική σύγκρουση δύο αυτοκινήτων που τρέχουν το καθένα με 50 χλμ/ώρα είναι ισοδύναμη σε καταστροφικές συνέπειες με τη σύγκρουση του ενός αυτοκίνητου σε τοίχο, όταν όμως το αυτοκίνητο τρέχει με 100 χλμ/ώρα, δηλαδή 50+50, το άθροισμα των δύο ταχυτήτων. Πράγματι, περίπου έτσι είναι όταν οι ταχύτητες v₁ και v₂ είναι πολύ μικρές σε σχέση με την ταχύτητα του φωτός· όσο όμως τα v₁ και v₂ πλησιάζουν την ταχύτητα του φωτός, τόσο πιο λάθος είναι το απλό άθροισμα των ταχυτήτων.

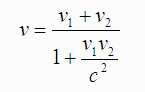
Ο σωστός τύπος του αθροίσματος (v) των ταχυτήτων v₁ και v₂, όπου c είναι η ταχύτητα του φωτός

Ο παραπάνω τύπος δίνει το “σχετικιστικό” (πραγματικό) άθροισμα των ταχυτήτων. Παρατηρούμε οτι αν τα v₁ και v₂ είναι πολύ μικρά σε σχέση με την ταχύτητα του φωτός (c), τότε το v γίνεται πρακτικά ίσο με το άθροισμα v₁ και v₂ (επειδή το c² είναι πολύ μεγάλος αριθμός, κάνοντας τον παρονομαστή του μεγάλου κλάσματος πρακτικά ίσο με 1). Επίσης παρατηρούμε οτι αν τα v₁ και v₂ είναι καί τα δύο ίσα με c, τότε το v γίνεται κι αυτό ίσο με c! (Επειδή v = (c + c) / (1 + c·c/c²) = 2c / (1 + c²/c²) = 2c / (1 + 1) = 2c / 2 = c.) Αυτή η παρατήρηση σημαίνει οτι όσο μεγάλες ταχύτητες και να προσθέτουμε, εφόσον είναι μικρότερες από c, το άθροισμά τους δεν μπορεί ποτέ να ξεπεράσει το c. Άρα, εφόσον ξεκινάμε από σχετική ακινησία, δεν μπορούμε ποτέ να ξεπεράσουμε την ταχύτητα του φωτός.

Συμπέρασμα της θεωρίας της σχετικότητας:
Η ταχύτητα του φωτός είναι μια οριακή ταχύτητα στη φύση.

Προσοχή: το παραπάνω δεν σημαίνει οτι απαγορεύεται να υπάρχει στη φύση οντότητα κινούμενη με ταχύτητα μεγαλύτερη του φωτός! Το “οριακή ταχύτητα” σημαίνει οτι δεν είναι δυνατόν κάποιο κινούμενο σώμα με μη-μηδενική μάζα να φτάσει ακριβώς στην ταχύτητα του φωτός. Δεν αποκλείεται όμως να υπάρχουν φυσικά σώματα (π.χ. σωματίδια) που κινούνται με ταχύτητα πάντοτε μεγαλύτερη του φωτός. Τα θεωρητικά αυτά σωματίδια έχουν ονομαστεί “ταχυόνια” (κι ας μην έχει εντοπιστεί μέχρι σήμερα κανένα· αγγλ.: tachyons). Σύμφωνα με τη σχετικότητα, τα ταχυόνια (εφόσον υπάρχουν) είναι αδύνατο να επιβραδύνουν ώστε να “σιγανέψουν” την ταχύτητά τους και να την κάνουν ακριβώς ίση με εκείνη του φωτός (πόσω μάλλον να την κάνουν μικρότερη ή να σταματήσουν τελείως ως προς εμάς, τους παρατηρητές). Η ταχύτητα του φωτός λοιπόν αποτελεί ένα φράγμα ταχυτήτων στη φύση.

Επίσης η σχετικότητα κάνει και μια δεύτερη αξιωματική υπόθεση: οτι οι νόμοι της φυσικής είναι οι ίδιοι για όλους τους παρατηρητές που κινούνται με ευθύγραμμη ομαλή κίνηση. Άρα κανένας από αυτούς τους παρατηρητές δεν είναι σε θέση να ισχυριστεί οτι: «Εγώ είμαι στην πραγματικότητα ο μόνος ακίνητος, και όλοι οι άλλοι κινούνται ως προς εμένα» («στην πραγματικότητα» ως προς τι; η κίνηση είναι σχετική ως προς κάτι άλλο, εξ ου και “θεωρία της σχετικότητας”).

Από τα δύο αυτά αξιώματα έπεται οτι δεν υπάρχει ο “απόλυτος χρόνος” της φυσικής του Νιούτον. Δηλαδή όταν ένα ρολόι δείχνει μεσημέρι της 30^ής Ιουνίου του 1905, δεν σημαίνει οτι είναι μεσημέρι της ίδιας ημέρας και στον Άρη, ή στο Σείριο, ή σε έναν άλλο γαλαξία. Δεν υπάρχει “παγκόσμιος χρόνος”, δηλ. παγκόσμιο ρολόι που να χτυπά τα δευτερόλεπτα ακαριαία σ’ όλο το σύμπαν (κάτι που είναι υπόθεση της κλασικής φυσικής). Δεν υπάρχουν ταυτόχρονα γεγονότα, παρά μόνο υπό την εξής έννοια: ας υποθέσουμε οτι γίνεται ένα γεγονός Α εδώ στη Γη, και την ίδια στιγμή φεύγει από τη Γη ένα φωτεινό σήμα, που ταξιδεύει προς τον Άρη. Μετά από 5 λεπτά, και τη στιγμή που φτάνει στον Άρη, συμβαίνει στον Άρη ένα γεγονός Β. Τότε λέμε οτι τα γεγονότα Α και Β είναι ταυτόχρονα, παρά το οτι για τους παρατηρητές της Γης και του Άρη έχουν μια χρονική απόσταση 5 λεπτών. Αν μπορούσε να υπάρξει ένας παρατηρητής που να ταξιδεύει μαζί με την ακτίνα φωτός, τότε γι’ αυτόν τον παρατηρητή τα Α και Β θα συνέβαιναν πραγματικά ταυτόχρονα, δηλαδή χωρίς ενδιάμεση χρονική υστέρηση. Γενικά, όλα τα γεγονότα που “συναντάει στο δρόμο-της” η ακτίνα φωτός, λέγονται ταυτόχρονα.

Από την προηγούμενη παρατήρηση έπεται οτι για μια ακτίνα φωτός τα πάντα συμβαίνουν την ίδια στιγμή, δηλαδή ο χρόνος είναι “παγωμένος”, δεν “ρέει”. Αν μπορούσαμε να έχουμε έναν παρατηρητή που να τρέχει με την ταχύτητα του φωτός, για τον παρατηρητή αυτόν ο χρόνος δεν θα κυλούσε καθόλου. (Βέβαια τέτοιος παρατηρητής δεν μπορεί να υπάρξει ποτέ, τόσο για λόγους φυσικής — κανένα σώμα με μη-μηδενική μάζα δεν μπορεί να φτάσει ακριβώς την ταχύτητα του φωτός — όσο και για λόγους νοολογίας, γιατί ένας “παρατηρητής” για τον οποίο ο χρόνος δεν ρέει δεν έχει μνήμη, άρα δεν μπορεί να παρατηρήσει τίποτα.) Μπορούμε όμως να φανταστούμε έναν παρατηρητή ο οποίος κινείται σχεδόν με την ταχύτητα του φωτός. Για τον παρατηρητή αυτόν, τα γεγονότα Α και Β της προηγούμενης παραγράφου συμβαίνουν πολύ γρήγορα, το ένα μετά το άλλο. Ενώ δηλαδή για τους παρατηρητές της Γης και του Άρη περνάνε 5 λεπτά μεταξύ των γεγονότων Α και Β, για τον παρατηρητή που κινείται με σχεδόν την ταχύτητα του φωτός περνάνε μόλις μερικά δευτερόλεπτα μεταξύ των Α και Β — τόσο πιο λίγα δευτερόλεπτα όσο πιο πολύ πλησιάζει η ταχύτητά του την ταχύτητα του φωτός. Για τους παρατηρητές της Γης και του Άρη, οι βιολογικοί ρυθμοί του κινούμενου παρατηρητή είναι εξαιρετικά βραδείς· δηλαδή, μπορεί π.χ. η καρδιά-του να χτυπήσει μόλις τρεις φορές κατά τη διάρκεια του πεντάλεπτου ταξιδιού-του. Αυτό το φαινόμενο ονομάζεται “διαστολή του χρόνου”.

Από την άποψη του ταχύτατα κινούμενου παρατηρητή, όχι μόνο το ταξίδι Γης–Άρη διαρκεί μόλις λίγα δευτερόλεπτα, αλλά και το διάστημα μεταξύ Γης και Άρη θα μοιάζει να έχει συσταλεί σε μερικές δεκάδες μέτρα. (Για μια ακτίνα φωτός, τα μήκη μηδενίζονται.) Αυτό το φαινόμενο ονομάζεται “συστολή του μήκους”.

Τα παράξενα αυτά φαινόμενα δεν τα παρατηρούμε στο οικείο-μας περιβάλλον, γιατί οι ταχύτητες με τις οποίες κινούμαστε είναι εξαιρετικά μικρές σε σύγκριση με την ταχύτητα του φωτός. Όταν οι ταχύτητες είναι τόσο μικρές όσο αυτές της καθημερινότητάς μας, τότε η κλασική φυσική του Νιούτον δίνει εξαιρετικά καλές προσεγγίσεις της φυσικής πραγματικότητας. Γιαυτό το λόγο συνεχίζουμε να χρησιμοποιούμε την κλασική φυσική για τα πρακτικά καθημερινά προβλήματα, αφού οι διορθώσεις που θα έκανε η σχετικιστική φυσική στις απαντήσεις της κλασικής θα ήσαν αμελητέες. Η σχετικιστική φυσική είναι απαραίτητη όταν οι ταχύτητες πλησιάζουν την ταχύτητα του φωτός, ή όταν — όπως θα δούμε αμέσως στα περί γενικής σχετικότητας — τα φυσικά συστήματα βρίσκονται μέσα σε πολύ ισχυρά βαρυτικά πεδία.

Γενική θεωρία της σχετικότητας

Ο Αϊνστάιν θα μπορούσε να μείνει με τη μία επανάσταση του 1905, έχοντας ήδη καταρρίψει (ή μάλλον επεκτείνει και συμπληρώσει, ως ένα βαθμό) την κλασική φυσική. Στην πραγματικότητα όμως ο Αϊνστάιν είναι υπεύθυνος και για τη δεύτερη επανάσταση στο χώρο της φυσικής, καθώς τα έτη 1915–1916 πρότεινε τη θεωρία της γενικής σχετικότητας, που επανατοποθετεί την απάντηση στο ερώτημα του τί είναι η βαρύτητα. Η κλασική φυσική λέει οτι η βαρύτητα είναι απλώς “μια δύναμη” (που μυστηριωδώς έχουν τα σώματα με μάζα, όπως η Γη, ο Ήλιος, αλλά και μια καρφίτσα). Η γενική θεωρία της σχετικότητας λέει οτι κάθε σώμα με μάζα προκαλεί ένα “βαθούλωμα” στον τριδιάστατο χώρο, και οτι οι τροχιές των σωμάτων που λέμε οτι “έλκονται από τη βαρύτητα” παραμορφώνονται από το βαθούλωμα αυτό. Αν φανταστούμε τον τριδιάστατο χώρο σαν ένα διδιάστατο τεντωμένο σεντόνι, τότε ένας αστέρας (όπως ο Ήλιος) μοιάζει με μια βαριά μπάλα του μπόουλινγκ που προκαλεί ένα βαθούλωμα στο σεντόνι. Η Γη, στην αναλογία αυτή, μοιάζει με μια μικρότερη μπάλα (π.χ. ένα βώλο), που προκαλεί ένα μικρότερο βαθούλωμα.

Το “βαθούλωμα” στο χώρο (εδώ σε 2 διαστάσεις)
που προκαλεί οποιοδήποτε σώμα με μάζα

Η περιφορά ενός πλανήτη γύρω από έναν αστέρα μπορεί να παρομοιαστεί με το αέναο στριφογύρισμα του πλανήτη στο “τοίχωμα” του βαθουλώματος, όπως δείχνει το επόμενο σχεδιάγραμμα:

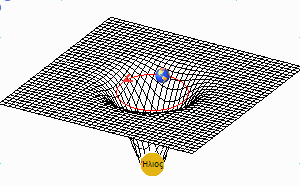
Η Γη περιφέρεται στο τοίχωμα του βαθουλώματος του Ήλιου

Το στριφογύρισμα είναι “αέναο” επειδή στο διάστημα δεν υπάρχει τριβή ώστε ο πλανήτης να χάσει ενέργεια και να πέσει προς τον αστέρα ακολουθώντας μια σπειροειδή τροχιά. Αυτό ακριβώς όμως παθαίνει ένας τεχνητός δορυφόρος που αχρηστεύεται, παύει να λειτουργεί ο μηχανισμός-του που διορθώνει την τροχιά-του και που τον διατηρούσε σε περιφορά γύρω από τη Γη (παρά την τριβή της — έστω αραιότατης — ατμόσφαιρας), και τελικά πέφτει με σπειροειδή πορεία μέσα στο βαθούλωμα της Γης, ώσπου να συγκρουστεί με τον πλανήτη.

Μια πολύ παραστατική απεικόνιση του “στριφογυρίσματος” των πλανητών στο βαθούλωμα του Ήλιου μπορούμε να δούμε εδώ, όπου παρατηρούμε οτι όσο πιο μέσα στο βαθούλωμα (κοντά στον Ήλιο) είναι ο πλανήτης, τόσο πιο γρήγορα στριφογυρίζει. Το όλο σύστημα θυμίζει δίνη στην οποία έχουν παγιδευτεί οι πλανήτες, χωρίς όμως ποτέ να παρασύρονται μέσα στη δίνη και να πέφτουν στον Ήλιο γιατί όπως είπαμε δεν υπάρχει τριβή στο χώρο του διαστήματος.

Μπορούμε επίσης να φανταστούμε έναν αστεροειδή που έρχεται με μεγάλη ταχύτητα και περνάει “ξυστά” από τη Γη, αλλά καθώς εισέρχεται στο βαθούλωμα της Γης, η ευθεία πορεία-του εκτρέπεται και γίνεται καμπύλη· λόγω όμως της μεγάλης ταχύτητάς του, ξεφεύγει από το βαθούλωμα της Γης, και συνεχίζει σε ευθεία πορεία και πάλι, έχοντας “στραβώσει” την αρχική-του ευθεία λόγω του βαθουλώματος της Γης.

Το ίδιο ακριβώς συμβαίνει και σε μια ακτίνα φωτός που περνάει “ξυστά” από τη Γη ή τον Ήλιο. Βέβαια το φως δεν έχει μάζα (“μάζα ηρεμίας” όπως λέγεται)· το φως είναι σκέτη ενέργεια, οπότε θα περίμενε κανείς οτι δεν θα ελκόταν από ένα ουράνιο σώμα ώστε να “στραβώσει” η πορεία-του. Και όμως, σύμφωνα με τον τύπο E = mc², κάθε ποσότητα ενέργειας αντιστοιχεί σε μια ισοδύναμη ποσότητα μάζας. Για το λόγο αυτό, και η ακτίνα φωτός αντιστοιχεί σε μια απειροελάχιστη ποσότητα μάζας, που έλκεται από το ουράνιο σώμα (π.χ. τον αστέρα), και άρα “στραβώνει”. Αυτό παριστάνεται στο επόμενο σχεδιάγραμμα:

Στο διάγραμμα βλέπουμε οτι η ακτίνα από το αστέρι Α κάμπτεται από το βαθούλωμα (βαρυτικό πεδίο) του Ήλιου, και φτάνει στη Γη. Έτσι μπορούμε να δούμε το αστέρι, αλλά στη θέση Β (γιατί για μας κάθε ακτίνα φωτός είναι ευθεία), ενώ αν δεν ίσχυε η σχετικότητα το αστέρι θα έπρεπε να μη φαινόταν γιατί θα το έκρυβε ο Ήλιος, αφού στην πραγματικότητα το αστέρι είναι στη θέση Α.

Αυτή ήταν και η πρώτη επιβεβαίωση της γενικής σχετικότητας το 1919, όταν έγινε μια ολική έκλειψη Ηλίου. Χωρις έκλειψη, το αστέρι είναι αδύνατο να παρατηρηθεί, αφού το φως-του εξαφανίζεται μέσα στη λάμψη του ουρανού της Γης, που προκαλεί το εκτυφλωτικό φως του Ήλιου. Κατά τη διάρκεια μιας ολικής έκλειψης όμως ο ουρανός της Γης παύει να λάμπει και φαίνονται ακόμα και τα αστέρια που είναι κοντά στον Ήλιο. Το 1919, ο Βρετανός Sir Arthur Eddington έστειλε αποστολές σε τρία μέρη της Γης ώστε να κάνουν μετρήσεις για να βρεθεί αν ισχύει η θεωρία του Αϊνστάιν. Οι μετρήσεις έγιναν, και αφού έγιναν και οι υπολογισμοί της οπτικής μετατόπισης του αστέρα στη θέση Β, ανακοινώθηκε οτι το ποσό της μετατόπισης συμφωνούσε με την πρόβλεψη της θεωρίας της σχετικότητας. Πολλά χρόνια αργότερα διαπιστώθηκε οτι οι μετρήσεις εκείνες δεν ήσαν ακριβείς, και οτι από σύμπτωση έδωσαν καταφατικό αποτέλεσμα. (Το ίδιο πείραμα όμως έχει επαναληφθεί πολλές φορές από τότε με ακρίβεια, και πάντοτε έχει επιβεβαιωθεί η σχετικιστική θεωρία.) Πάντως, έστω και λίγο με τη βοήθεια της τύχης, το πείραμα αυτό θεωρήθηκε σαν επιβεβαίωση της θεωρίας της σχετικότητας την εποχή εκείνη, και η δημοτικότητα του Αϊνστάιν εκτοξεύθηκε στα ύψη. Αυτό έμελλε να παίξει σπουδαίο ρόλο αργότερα, γιατί σαν κορυφαίο επιστήμονα δεν τόλμησαν να τον στείλουν — ως Εβραίο — σε στρατόπεδα συγκέντρωσης οι ναζί, δύο δεκαετίες αργότερα. Πάντως τη δεκαετία του 1930 ο Αϊνστάιν αντιμετώπιζε ένα πολύ εχθρικό περιβάλλον στη Γερμανία, όπου κινδύνευε η ζωή-του, και το 1933 υποχρεώθηκε να μεταναστεύσει στις Η.Π.Α., όπου και πήρε την Αμερικανική υπηκοότητα. Από τότε, και μέχρι το θάνατό του το 1955, υπήρξε καθηγητής στο πανεπιστήμιο του Πρίνστον.

Αξιοσημείωτο είναι οτι όπως και στην ειδική θεωρία της σχετικότητας, έτσι και στη γενική, ο χρόνος διαστέλλεται και τα μήκη συστέλλονται μέσα στο βαθούλωμα του χωροχρόνου ενός πλανήτη ή αστέρα. Όσο πιο μεγάλο το βαθούλωμα, τόσο πιο μεγάλη η διαστολή του χρόνου και η συστολή του μήκους. “Μεγάλο βαθούλωμα” σημαίνει ισχυρό βαρυτικό πεδίο, δηλαδή ουράνιο σώμα με μεγάλη μάζα. Υπάρχουν αστέρες, οι λεγόμενοι “αστέρες νετρονίων”, που έχουν τεράστια πυκνότητα ύλης (πολλές τάξεις μεγέθους πιο πυκνή από την πυκνότερη που μπορούμε να συναντήσουμε στη Γη, που είναι το μεταλλικό στοιχείο ιρίδιο). Επομένως, στην επιφάνεια ενός αστέρα νετρονίων ο χρόνος είναι εξαιρετικά διεσταλμένος, δηλαδή “περνάει πολύ αργά” για μας τους εξωτερικούς παρατηρητές. Υπάρχουν ουράνια σώματα με ακόμα πιο μεγάλη πυκνότητα ύλης — άπειρη, στην πραγματικότητα — τα οποία λέγονται “μαύρες τρύπες”.

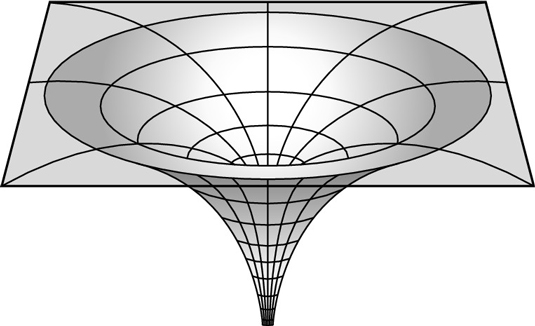
Σχηματική παραμόρφωση χωροχρόνου από αστέρα νετρονίων, ή μαύρη τρύπα

Στο παραπάνω σχεδιάγραμμα, αν πρόκειται για αστέρα νετρονίων, πρέπει να φανταστούμε τον αστέρα να είναι κάπου στο βάθος του “πηγαδιού”, ενώ για μια μαύρη τρύπα πρέπει να φανταστούμε το πηγάδι να συνεχίζεται χωρίς πάτο, μέχρι το άπειρο. Σε μια μαύρη τρύπα, η διαστολή του χρόνου απειρίζεται, δηλαδή ο χρόνος σταματάει εντελώς.

Με τί μοιάζει μια μαύρη τρύπα; Ονομάζεται έτσι γιατί η βαρυτική-της έλξη είναι τόσο μεγάλη που τίποτε, ούτε ακόμη και το φως, δεν μπορεί να διαφύγει αν βρεθεί κοντά στη μαύρη τρύπα, σε μια ακτίνα μικρότερη από το λεγόμενο “ορίζοντα γεγονότων”. Εφόσον ούτε το φως διαφεύγει, οι μαύρες τρύπες οφείλουν να εμφανίζονται... μαύρες. Το παρακάτω διάγραμμα μας δίνει μια ιδέα:

Έτσι θα μπορούσε να μοιάζει από κοντά μια μαύρη τρύπα

Ενώ η μαύρη τρύπα καθαυτό είναι — ως μαύρη — αόρατη, εντούτοις πρέπει να σκιάζει το υπόβαθρο των αστέρων που βρίσκονται από πίσω-της, και πρέπει να προκαλεί ένα οπτικό φαινόμενο όπως ένας φακός, καμπυλώνοντας ισχυρά το φως τον αστέρων που καλύπτει, και εμφανίζοντάς τους στην περιφέρειά της. (Πρόκειται για το ίδιο φαινόμενο καμπύλωσης του φωτός που συζητήθηκε παραπάνω.) Μαύρες τρύπες δεν έχουν παρατηρηθεί μέχρι στιγμής απευθείας (καθώς αυτό είναι πολύ δύσκολο), αλλά έμμεσα, λόγω των επιδράσεων που έχουν με τα γειτονικά-τους άστρα. Οι αστροφυσικοί έχουν βάσιμους λόγους να πιστεύουν οτι το σύστημα X-1 του αστερισμού του Κύκνου περιλαμβάνει μια μαύρη τρύπα· επίσης οτι μια μεγάλη μαύρη τρύπα υπάρχει στο κέντρο κάθε μεγάλου γαλαξία, ασφαλώς και του δικού-μας.

Βλέπουμε λοιπόν πώς η γενική σχετικότητα μετέτρεψε το πρόβλημα της βαρύτητας σε πρόβλημα γεωμετρίας. Η γεωμετρία που ισχύει όταν ο χώρος καμπυλώνεται (αποκτά βαθουλώματα) λόγω σωμάτων με μάζα δεν είναι η Ευκλείδεια, αλλά η υπερβολική (που τη συναντήσαμε ήδη στα περί μη-Ευκλείδειων γεωμετριών). Ας θυμηθούμε οτι στην υπερβολική γεωμετρία το άθροισμα των γωνιών ενός τριγώνου είναι μικρότερο των 180°, και ο λόγος της περιμέτρου διά τη διάμετρο ενός κύκλου είναι μικρότερος του αριθμού π. Παρατηρείστε πώς τα “βαθουλώματα” του καμπύλου χώρου στα προηγούμενα σχεδιαγράμματα μοιάζουν με τις επιφάνειες στις οποίες είπαμε οτι ισχύει η υπερβολική γεωμετρία, όπως το “σαμάρι” και η “ψευδοσφαίρα”.

Όμως η γενική σχετικότητα είναι μια ακόμα πιο γενική θεωρία, που μπορεί να περιγράψει όχι απλώς τον καμπύλο χώρο, αλλά τον τετραδιάστατο χωρο-χρόνο, και όχι μόνο σε τοπικό επίπεδο, αλλά και σε επίπεδο ολόκληρου του σύμπαντος. Η γενικευμένη γεωμετρία που χρησιμοποιούμε για να περιγράψουμε το σύμπαν — ή άλλα σύμπαντα — είναι η Ριμάνεια γεωμετρία (που επίσης ήδη αναφέρθηκε στα περί γεωμετριών).

Μία ακόμη σπουδαία επιτυχία της θεωρίας της σχετικότητας είναι η εξήγηση της “προήγησης” (precession) του περιήλιου του Ερμή. Όπως ειπώθηκε στο εδάφιο περί νόμων του Κέπλερ, η τροχιά κάθε πλανήτη γύρω από έναν αστέρα είναι έλλειψη, με τον αστέρα να κατέχει τη μια εστία της έλλειψης. Είχε όμως παρατηρηθεί οτι ο πλανήτης Ερμής δεν ακολουθεί ακριβώς μια έλλειψη, αλλά κάτι σαν έλλειψη η οποία περιστρέφεται (πολύ αργά) γύρω από τον αστέρα, όπως δείχνει το παρακάτω σχήμα:

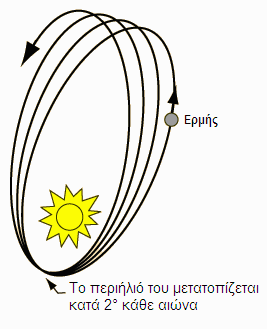
Το “περιήλιο” είναι το σημείο της τροχιάς στο οποίο ο πλανήτης είναι πιο κοντά στον Ήλιο. Είχε λοιπόν παρατηρηθεί οτι το περιήλιο του Ερμή μετατοπίζεται (“προηγείται”) κατά 2 μοίρες περίπου κάθε αιώνα, γεγονός που δεν μπορούσε να εξηγηθεί με την κλασική φυσική και τους νόμους του Κέπλερ. Εξηγήθηκε όμως μέσω της γενικής θεωρίας της σχετικότητας. Ας σημειωθεί οτι η προήγηση του περιήλιου συμβαίνει σε κάθε πλανήτη, απλώς είναι τόσο πιο εύκολα παρατηρήσιμη όσο πιο κοντά στον Ήλιο βρίσκεται ο πλανήτης (άρα περιφέρεται πιο γρήγορα), και όσο πιο ελλειπτική (λιγότερο κυκλική) είναι η τροχιά-του. Ο Ερμής είναι βέβαια ο κοντινότερος πλανήτης στον Ήλιο, και η τροχιά-του δεν είναι ιδιαίτερα κυκλική, γιαυτό και η παρατήρηση αυτή έγινε μέσω του Ερμή.

Ανάμεσα στις πάμπολλες εφαρμογές της θεωρίας της σχετικότητας υπάρχουν καθημερινές-μας συσκευές, όπως η συσκευή GPS του αυτοκινήτου που μας αναγγέλει την ακριβή θέση-μας. (Χωρίς τη σχετικότητα, το ρολόι του δορυφόρου που ενημερώνει τη συσκευή θα έτρεχε ανεξήγητα πιο γρήγορα από όλα τα ρολόγια της Γης.) Χωρίς τη σχετικότητα θα ήταν αδύνατο να κατανοήσουμε τη συμπεριφορά των στοιχειωδών σωματιδίων που κινούνται με πολύ μεγάλες ταχύτητες στα εργαστήρια που κάνουν έρευνες πυρηνικής φυσικής. Επίσης, μια σπουδαία εφαρμογή είναι η παραγωγή ενέργειας από πυρηνικά εργοστάσια (που συνδέεται με την απεξάρτηση από το πετρέλαιο). Απόρροια της σχετικότητας είναι και τα πυρηνικά όπλα, για τα οποία θα μιλήσουμε αργότερα.

Η εποχή των αρχών του 20^ού αιώνα φαινόταν ώριμη για μεγάλες ανακαλύψεις στη φυσική. Είδαμε οτι η μια βαθειά τομή έγινε από τον Αϊνστάιν, που ανασκεύασε την κλασική φυσική των προηγούμενων αιώνων. Όμως η σχετικότητα του Αϊνστάιν ήταν μια θεωρία που αφορούσε στο μακρόκοσμο, σε μεγάλες αποστάσεις χώρου και χρόνου. Ταυτόχρονα, άλλοι φυσικοί εξέταζαν το μικρόκοσμο, τις ιδιότητες και τη σύσταση των ατόμων. Μέσω της έρευνας του μικρόκοσμου ξεκίνησε η δεύτερη μεγάλη βαθειά τομή στη φυσική.

Marie Skłodowska Curie (Μαρί Σκλοντόβσκα Κιουρί, 1867 – 1934)· έρευνες για τη ραδιενέργεια

Η Κιουρί χρησιμοποίησε το ηλεκτρόμετρο που είχε κατασκευάσει 15 χρόνια νωρίτερα ο σύζυγός της Πιέρ με τον αδελφό-του, και διαπίστωσε οτι οι ακτίνες από το ουράνιο έκαναν τον αέρα γύρω από άλατα ουρανίου να είναι αγώγιμος στον ηλεκτρισμό. Βρήκε μάλιστα οτι αυτή η ηλεκτρική δράση εξαρτιόταν αποκλειστικά και μόνο από την ποσότητα του ουρανίου. Άρα δεν επρόκειτο για κάποια αλληλεπίδραση του ουρανίου με οτιδήποτε άλλο που ήταν παρόν, αλλά για μια εγγενή ιδιότητα του ουρανίου. Στα πειράματα αυτά χρησιμοποίησε δύο άλατα του ουρανίου: τον πισσουρανίτη και τον τορβενίτη (ή χαλκολίτη), και βρήκε οτι ο πισσουρανίτης ήταν τέσσερις φορές πιο ενεργός από το ίδιο το ουράνιο, ενώ ο τορβενίτης ήταν δύο φορές πιο ενεργός. Συμπέρανε έτσι οτι τόσο ο πισσουρανίτης όσο και ο τορβενίτης περιέχουν μια ουσία η οποία είναι υπεύθυνη για την ακτινοβολία, ενώ το ουράνιο έχει λιγότερη από αυτή την ουσία, την οποία βάλθηκε ν’ ανακαλύψει εξετάζοντας τόννους ολόκληρους από πισσουρανίτη, μαζί με το σύζυγό της. Τελικά μέσω της εργασίας αυτής ανακάλυψε δύο νέα χημικά στοιχεία: το πολώνιο (που ονόμασε έτσι προς τιμήν της πατρίδας-της), και το — πολύ πιο δύσκολο ν’ απομονωθεί — ράδιο, που ήταν και η “ουσία” η κυρίως υπεύθυνη για την ακτινοβολία. Την τελευταία την ονόμασε ραδιενέργεια. Το 1903, το Νόμπελ φυσικής απονεμήθηκε από κοινού στη Μαρία Κιουρί, στον Πιέρ Κιουρί, και στον Ανρί Μπεκερέλ, για την έρευνά τους στο φαινόμενο της ραδιενέργειας. Το 1911, το Νόμπελ χημείας απονεμήθηκε επίσης στην Κιουρί για την ανακάλυψή της των στοιχείων πολώνιο και ράδιο.

Κατά τη διάρκεια του 1^ου Παγκοσμίου Πολέμου η Κιουρί προώθησε τη χρήση κινητών μονάδων ραδιογραφίας (ακτίνων Χ), για τη διάγνωση των τραυμάτων των τραυματιών πολέμου. Αυτές οι μονάδες ήσαν αυτοκίνητα της εποχής εκείνης, εφοδιασμένα με λυχνίες που, με χρήση ραδίου, παρήγαγαν ένα άχρωμο ραδιενεργό αέριο. Το αέριο αυτό ταυτοποιήθηκε αργότερα σαν το βαρύτερο ευγενές αέριο, το ραδόνιο. Η Κιουρί ασφαλώς εκτέθηκε σε υπερβολική δόση ραδιενέργειας την περίοδο εκείνη, οπότε βέβαια ήταν άγνωστη η καταστροφική δράση της ραδιενέργειας στον οργανισμό κάθε έμβιου όντος. Η Κιουρί πέθανε το 1934 από απλαστική αναιμία, που είναι σχεδόν βέβαιο οτι ήταν αποτέλεσμα της χρόνιας έκθεσής της σε ραδιενέργεια.

Πέρα από τις σπουδαίες επιστημονικές-της ανακαλύψεις, η Μαρία Κιουρί βοήθησε και στο να κατατρωθεί το αρνητικό στερεότυπο που ήθελε τις γυναίκες ανίκανες να κάνουν σημαντικές συνεισφορές στην επιστήμη. Η Κιουρί παραμένει ο μοναδικός άνθρωπος με δύο Νόμπελ σε επιστημονικούς τομείς. (Ο μόνος άλλος με δύο Νόμπελ, ο Linus Pauling, έχει ένα Νόμπελ χημείας και ένα ειρήνης.)

Ernest Rutherford (Έρνεστ Ράδερφορντ, 1871 – 1937)· έρευνες για τη σύσταση του ατόμου

Ο Rutherford παρατήρησε οτι όταν μια ποσότητα ραδιενεργού υλικού διασπάται, παίρνει πάντα τον ίδιο χρόνο για να διασπαστεί η μισή από την ποσότητα του υλικού. Δηλαδή, ας πούμε οτι έχουμε 1 κιλό (χονδρικά) ραδιενεργό υλικό, και οτι παίρνει 1 ώρα για να διασπαστεί το μισό, δηλαδή μένουμε με 500 γραμ. ραδιενεργού υλικού σε μία ώρα· σε άλλη μία ώρα, θα μας μείνουν 250 γραμμάρια· σε μία ώρα ακόμα, θα μας μείνουν 125 γραμμάρια· κ.ο.κ., δηλαδή κάθε ώρα θα μας μένει η μισή από την προηγούμενη ποσότητα. Ο χρόνος που παίρνει για να διασπαστεί η μισή ποσότητα του ραδιενεργού υλικού λέγεται ημιζωή του υλικού (1 ώρα στο παράδειγμα).

Η παρατήρηση αυτή έχει τεράστια σημασία για τη χρονολόγηση υλικών, π.χ. πετρωμάτων, απολιθωμάτων οστών ή φυτών (που είναι βέβαια κι αυτά πετρώματα), κλπ. Ο λόγος είναι οτι όταν δημιουργείται το απολίθωμα (δηλ. η πέτρα), περικλείει εντός-του κάποια ποσότητα ραδιενεργού υλικού. Αν η ημιζωή του υλικού είναι αρκετές χιλιάδες χρόνια, τότε από την ποσότητα που απέμεινε όταν ανακαλύπτουμε το απολίθωμα ή το πέτρωμα μπορούμε να υπολογίσουμε πότε δημιουργήθηκε, δηλαδή να βρούμε την ηλικία-του. Για ηλικίες που φτάνουν τα 1-2 δισεκατομμύρια έτη (π.χ. για τους πρώτους πολυκύτταρους οργανισμούς), ανιχνεύονται ραδιενεργά υλικά με πολύ μεγάλη ημιζωή· για ηλικίες που κυμαίνονται σε μερικές δεκάδες χιλιάδες ή λίγα εκατομμύρια έτη (π.χ. προγονικά είδη του ανθρώπου), ανιχνεύονται ραδιενεργά υλικά με μικρή ημιζωή. Αυτή είναι η βασική μέθοδος εύρεσης ηλικιών απολιθωμάτων στην παλαιοντολογία, που χρησιμοποιείται μέχρι σήμερα (βλ. μάθημα Β1).

Το 1903, ο Rutherford παρατήρησε οτι ένα είδος ακτινοβολίας που παραγόταν από το στοιχείο ράδιο είχε εξαιρετικά μεγάλη διαπερατότητα — πολύ μεγαλύτερη από εκείνη των ακτίνων άλφα και βήτα. Την ακτινοβολία αυτή ο Rutherford ονόμασε “ακτίνες γάμμα”, οι οποίες αργοτερα έγινε κατανοητό οτι είναι φωτόνια πολύ μεγάλης ενέργειας. (Τις ακτίνες γάμμα τις συναντήσαμε στην περιγραφή του ηλεκτρομαγνητικού φάσματος, στο εδάφιο περί Röntgen.)

Τα πειράματα όμως που τον έκαναν ακόμα πιο διάσημο, ο Rutherford τα εκτέλεσε μετά την απονομή του Νόμπελ. Στα πειράματά του αυτά (που έγιναν υπό την επίβλεψή του και εκτελέστηκαν από τους Geiger και Marsden), ο Rutherford βομβάρδιζε ένα λεπτό φύλλο χρυσού με ακτίνες άλφα, και παρατηρούσε πώς σκεδάζονται (δηλαδή χτυπούν και αλλάζουν διεύθυνση) οι ακτίνες αυτές πάνω στα άτομα του χρυσού. Ο σκοπός ήταν να μελετηθεί η σύσταση των ατόμων (του χρυσού στην προκειμένη περίπτωση). Μέχρι τότε οι επιστήμονες είχαν βρει οτι κάθε άτομο έχει μέσα-του θετικά και αρνητικά ηλεκτρικά φορτία, όμως δεν ήξεραν τίποτε άλλο: ούτε τις ιδιότητες των φορτίων αυτών, ούτε το πώς ήταν διαρρυθμισμένα στο εσωτερικό του ατόμου. Επικρατούσε λοιπόν η ιδέα οτι τα θετικά και αρνητικά φορτία ήσαν άτακτα ριγμένα μέσα στο άτομο, ας πούμε σαν τις σταφίδες μέσα στο σταφιδόψωμο. Καθώς θα έρχονταν απ’ έξω με μεγάλη ταχύτητα οι ακτίνες άλφα, θα έπρεπε να χτυπήσουν μερικές από τις “σταφίδες” (τα θετικά και αρνητικά φορτία), και να σκεδαστούν υπό κάποιες μικρές γωνίες. Η έκπληξη του Rutherford και των συνεργατών-του ήταν ασφαλώς πολύ μεγάλη όταν διαπίστωσαν οτι, ναι μεν οι περισσότερες ακτίνες άλφα διαπερνούσαν το φύλλο χρυσού, αλλά κάποιες ελάχιστες σκεδάζονταν όχι υπό μικρές, αλλά υπό τεράστιες γωνίες. Μερικές μάλιστα γυρνούσαν προς τα πίσω! Ήταν σαν να πυροβολούσε κανείς το σταφιδόψωμο, και αντί όλες οι σφαίρες να διαπερνούν τη μάζα-του, μερικές απ’ αυτές να ανακλώνται στις “σταφίδες” και να επιστρέφουν πίσω! Ο Rutherford συμπέρανε οτι η θεωρία του “σταφιδόψωμου” για το άτομο δεν ήταν σωστή. Αυτό που θα έπρεπε να συμβαίνει ήταν οτι όλο το άτομο ήταν σχεδόν κενό (εξηγώντας έτσι γιατί οι περισσότερες ακτίνες άλφα το διαπερνούσαν σαν να μη συνέβαινε τίποτα), ενώ όλη η μάζα-του ήταν συγκεντρωμένη σε ένα πολύ μικρό σημείο, τον πυρήνα. Οι ακτίνες άλφα που σπάνια τύχαινε να χτυπήσουν τον πυρήνα σκεδάζονταν υπό πολύ μεγάλες γωνίες, εξηγώντας έτσι τις παρατηρήσεις των πειραμάτων αυτών.

Το πόσο μικρός είναι ο χώρος όπου είναι συγκεντωμένη η μάζα του ατόμου — δηλαδή ο πυρήνας — σε σχέση με το όλο άτομο είναι δύσκολο να το αντιληφθεί κανείς. Ο πυρήνας είναι κάπου 20.000 φορές μικρότερος σε διάμετρο από το άτομο! Δηλαδή αν το άτομο είχε το μέγεθος ενός δωματίου (με μήκος π.χ. 5 μέτρα), τότε ο πυρήνας θα ήταν σαν την τελεία στο τέλος αυτής της πρότασης, και θα βρισκόταν στο μέσον του δωματίου.

Το ατομικό μοντέλο του Niels Bohr (Νιλς Μπορ, 1885 – 1962)

Βάσει των πειραμάτων του Rutherford και άλλων δεδομένων που ήσαν τότε γνωστά, το 1913 ο Δανός φυσικός Niels Bohr διατύπωσε το “ατομικό μοντέλο”, δηλαδή το απο τί θα έπρεπε ν’ αποτελείται ένα άτομο.

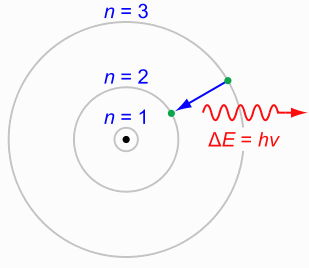Η ιδέα του Bohr (η οποία είναι σωστή) ήταν οτι κάθε στοιβάδα μπορεί να έχει ένα συγκεκριμένο αριθμό ηλεκτρονίων. Π.χ. η πρώτη στοιβάδα μπορεί να έχει μέχρι δύο ηλεκτρόνια. Αν το άτομο έχει τρία ή περισσότερα ηλεκτρόνια, τότε από το τρίτο και πάνω αυτά θα βρίσκονται στη δεύτερη στοιβάδα (σημειώνεται με n = 2 στο σχήμα). Η δεύτερη στοιβάδα μπορεί να έχει μέχρι 8 ηλεκτρόνια. Επομένως ένα άτομο που έχει ακριβώς 10 ηλεκτρόνια (αυτό είναι το άτομο του ευγενούς αερίου νέον) θα πρέπει να έχει 2 ηλεκτρόνια στην πρώτη στοιβάδα, και 8 στη δεύτερη. Το άτομο με ένα επιπλέον ηλεκτρόνιο (το νάτριο, με 11) πρέπει να έχει το 11ο ηλεκτρόνιο στην τρίτη στοιβάδα. Και ούτω καθεξής.

Το ατομικό μοντέλο του Bohr ερμήνευσε επίσης ένα άλλο φαινόμενο. Όταν ένα ηλεκτρόνιο που βρίσκεται π.χ. στη δεύτερη στοιβάδα δεχτεί ένα φωτόνιο, τότε ανεβαίνει στην τρίτη στοιβάδα, καθώς τώρα έχει μεγαλύτερη ενέργεια. Σε κάποια (ακαθόριστη) χρονική στιγμή, το ηλεκτρόνιο μπορεί να πέσει πάλι στη δεύτερη στοιβάδα, αποδίδοντας στο περιβάλλον ένα φωτόνιο. (Αυτό σημειώνεται με την κυματοειδή κόκκινη γραμμή, στα δεξιά στο σχήμα.) Το φωτόνιο έχει συχνότητα ν (επομένως ορισμένο χρώμα), και ενέργεια ίση με hν, όπου h είναι η σταθερά του Planck. Αυτή η απορρόφηση φωτονίων από ηλεκτρόνια και η απόδωση φωτονίων στο περιβάλλον λόγω της μετάπτωσης των ηλεκτρονίων σε χαμηλότερες στάθμες ενέργειας (στοιβάδες) συμβαίνει όποτε το φως πέφτει σε ένα υλικό σώμα και ανακλάται σ’ αυτό, συνήθως με κάποιο χρώμα ή χρώματα.

Παρ’ όλ’ αυτά, το μοντέλο του ατόμου του Bohr είναι αρκετά διαφορετικό από αυτό που θεωρούμε σωστό σήμερα. Συγκεκριμένα, τα ηλεκτρόνια δεν κινούνται σε “γραμμές” γύρω από τον πυρήνα (όπως ένα τραίνο πάνω σε ράγες), ούτε είναι μικρά σφαιρίδια. Είναι πολύ δύσκολο να περιγραφεί η πραγματικότητα, γιατί κανένα “οπτικό” μοντέλο (δηλ. που να μπορεί να ζωγραφιστεί) δεν μπορεί να την περιγράψει με ακρίβεια. Υπάρχει μόνο μια πιθανότητα να βρίσκεται το ηλεκτρόνιο σε ορισμένα σημεία του χώρου, και λιγότερη πιθανότητα να βρίσκεται σε άλλα. Οι τροχιές μοιάζουν κάπως με νέφη, αλλά πρόκειται για “νέφη” πιθανοτήτων. Επίσης τα νέφη αυτά μπορεί να μην έχουν σφαιρικό σχήμα, αλλά ωοειδές ή πεπλατυσμένο, κλπ. Επειδή όμως το μοντέλο του Bohr μπορεί να ζωγραφιστεί, αυτό είναι που βλέπουμε να χρησιμοποιείται ακόμα και σήμερα (εκτός φυσικής–χημείας) για να αποτυπωθεί η έννοια “άτομο”, όπως π.χ. στο παρακάτω σχήμα.

Τυπική (αλλά λανθασμένη) παράσταση ατόμου, που συναντάται συχνά ακόμα και σήμερα

Ο Bohr αποτέλεσε εμβληματική φυσιογνωμία στο χώρο της κβαντικής φυσικής. Αντίθετα με τη θεωρία της σχετικότητας, όπου η μορφή του Αϊνστάιν όχι απλώς δεσπόζει αλλά μοιάζει να είναι η μοναδική, στην κβαντική φυσική δεν υπάρχει ένας και μοναδικός επιστήμονας που να μπορεί να λάβει τον τίτλο του “πατέρα” του τομέα αυτού. Υπάρχουν πολλοί λαμπροί φυσικοί που συνεισέφεραν στην ανάπτυξη της θεωρίας, όπως θα δούμε παρακάτω. Ο Bohr θα μπορούσε να θεωρηθεί σαν ένας “πατριάρχης” μεταξύ αυτών.

Ανάπτυξη κβαντικής φυσικής

Από τη δεκαετία του 1920 και μετά, άρχισαν να συσσωρεύονται τα δεδομένα από παρατηρήσεις για τη φύση του ατόμου και των υποατομικών-του σωματιδίων. Η εικόνα για τη φύση και τις ιδιότητες των σωματιδίων αυτών ήταν τουλάχιστον αινιγματική. Τέτοια παραμένει ακόμη και σήμερα, και υπάρχει λόγος γι’ αυτό. Ο λόγος είναι οτι η κβαντική φυσική περιγράφει έναν κόσμο (τον κόσμο των κβάντα) στον οποίο ο άνθρωπος δεν εξελίχθηκε για ν’ αντιλαμβάνεται. Το είδος-μας (όπως και κάθε ζωικό είδος) εξελίχθηκε στο μακρόκοσμο, έναν κόσμο μεγάλων αντικειμένων — τουλάχιστον πολύ μεγαλύτερων από τα κβαντικά σωματίδια — στον οποίο ισχύουν οι νόμοι της λογικής του Αριστοτέλη, που λένε οτι π.χ. μια πέτρα είναι μια πέτρα, δεν μπορεί να είναι ταυτόχρονα πέτρα και σύννεφο. Στην κβαντική φυσική όμως, η Αριστοτέλεια λογική — με άλλα λόγια η κοινή λογική — δεν ισχύει. Εκεί μια οντότητα μπορεί να είναι ταυτόχρονα “πέτρα και σύννεφο”, ή για να το πούμε πιο συγκεκριμένα, κάθε υποατομικό σωματίδιο είναι ταυτόχρονα σωματίδιο και κύμα. Η παύση των νόμων της κοινής λογικής στο μικρόκοσμο της κβαντικής φυσικής είναι ανάλογη με την παύση των συμπερασμάτων της ανθρώπινης εμπειρίας στη θεωρία της σχετικότητας. Στη σχετικότητα, η ανθρώπινη εμπειρία παύει να δίνει σωστά συμπεράσματα επειδή το είδος-μας εξελίχθηκε σ’ έναν κόσμο με ταχύτητες εξαιρετικά μικρές σε σχέση με την ταχύτητα του φωτός. Στην κβαντική φυσική, και πάλι δεν ισχύει η ανθρώπινη εμπειρία και λογική, για λόγο παρόμοιο· δηλαδή επειδή, όπως προαναφέρθηκε, εξελιχθήκαμε για ν’ ανταποκρινόμαστε στους νόμους του μακρόκοσμου, και όχι του μικρόκοσμου.


Erwin Schrödinger Έρβιν Σρέντινγκερ 1887 – 1961	Werner Heisenberg Βέρνερ Χάιζενμπεργκ 1901 – 1976	Paul Dirac Πωλ Ντιράκ 1902 – 1984
Τρεις από τις μεγάλες φυσιογνωμίες που έδρασαν στο χώρο της κβαντικής φυσικής τον 20ό αιώνα: ο Αυστριακός Schrödinger, ο Γερμανός Heisenberg, και ο Άγγλος Dirac.

Μερικές από τις απρόσμενες και “περίεργες” (από την ανθρώπινη σκοπιά) ιδιότητες που ισχύουν στην κβαντική φυσική είναι οι εξής:

Η κβάντωση των φυσικών μεγεθών. Με τον όρο “κβάντωση” εννοείται η ύπαρξη διακριτών αντί συνεχών τιμών για μια ποσότητα. Ένα παράδειγμα κβάντωσης έχουμε ήδη συναντήσει: είδαμε οτι η ενέργεια που εκπέμπεται από ένα άτομο δεν μπορεί να έχει οποιαδήποτε τιμή (να είναι “συνεχής”), αλλά μπορεί μόνο να εκπεμφθεί κατά διακριτά “πακέτα”, που έχουν τιμή hν, όπου h είναι η σταθερά του Planck, και ν η συχνότητα (το “χρώμα”) του εκπεμπόμενου φωτόνιου. Το πακέτο (“κβάντο”) ενέργειας σ’ αυτήν την περίπτωση είναι το hν. Το οτι η ενέργεια είναι κβαντισμένη (με διακριτές, συγκεκριμένες τιμές) και όχι συνεχής μπορεί να μη μας προκαλεί καμιά ιδιαίτερη εντύπωση. Τί θα έλεγε όμως κανείς αν μάθαινε οτι και η στροφή ενός σωματιδίου είναι κβαντισμένη και όχι συνεχής; Στον οικείο-μας μακρόκοσμο, μια σβούρα μπορεί να στραφεί υπό οποιαδήποτε γωνία· το ίδιο κάνει και η γήινη σφαίρα, που καθώς στρέφεται κατά ομαλό και συνεχή τρόπο μέσα σε ένα 24-ωρο φέρνει κάθε τόπο π.χ. του βόρειου ημισφαιρίου το καλοκαίρι απέναντι στον Ήλιο. Αυτό όμως δεν συμβαίνει με τη “στροφή”, το “σπιν” όπως λέγεται, των υποατομικών σωματιδίων. Π.χ. το σπιν του ηλεκτρονίου είναι 1/2. Είναι σαν το ηλεκτρόνιο να εκτελεί μισή στροφή κάθε φορά. Αυτό είναι αδύνατο να το φανταστούμε με ένα οικείο αντικείμενο του μακρόκοσμου. Π.χ. μια σβούρα για να εκτελέσει μισή στροφή (δηλαδή 180°) πρέπει να περάσει από κάθε ενδιάμεση γωνία κατά συνεχή τρόπο. Και όμως, το ηλεκτρόνιο στρέφεται “απότομα” κατά 180°. Άλλα υποατομικά σωματίδια στρέφονται (πάντα “απότομα”) κατά 540° (σπιν 3/2), κλπ. Την κβάντωση του σπιν του ηλεκτρονίου περιέγραψε ο Paul Dirac με μαθηματικές εξισώσεις το 1930.

Ο κυματοσωματιδιακός δυϊσμός. Στην έννοια αυτή έγινε αναφορά νωρίτερα. Πρόκειται για την ιδέα οτι κάθε υποατομικό σωματίδιο μπορεί να περιγραφεί ταυτόχρονα καί σαν σωματίδιο, αλλά καί σαν κύμα. Η διαμάχη έχει τις ρίζες-της στην ελληνική αρχαιότητα. Ο Αριστοτέλης υποστήριξε οτι το φως είναι διακυμάνσεις μέσα στο στοιχείο του αέρα, ενώ ο Δημόκριτος είπε οτι το φως αποτελείται από — τί άλλο — άτομα (σωματίδια). Όπως είδαμε, η διαφωνία για τη φύση του φωτός μεταφέρθηκε κατά το 17^ο αιώνα στη διαμάχη μεταξύ Χάιχανς (φως = κύματα) και Νιούτον (φως = σωματίδια). Στην κβαντική φυσική βρέθηκε οτι όχι μόνο το φως (τα φωτόνια), αλλά και κάθε υποατομικό σωματίδιο έχει ταυτόχρονα και κυματικές ιδιότητες. Γιατί όμως όταν μελετάμε αντικείμενα του οικείου-μας μακρόκοσμου δεν τα βλέπουμε να έχουν κι αυτά κυματικές ιδιότητες, αφού και τα μακρο-αντικείμενα αποτελούνται από υποατομικά σωματίδια; Ο λόγος είναι οτι όταν δύο ή περισσότερα υποατομικά σωματίδια συμμετέχουν σε ένα σύστημα (π.χ. άτομο), τότε πρέπει να “προσθέσουμε” τα κύματά τους. Η πρόσθεση των κυμάτων έχει σαν αποτέλεσμα την εξασθένιση του κυματικού χαρακτήρα του συνόλου. Ακόμη κ’ ένα απειροελάχιστο κομματάκι ύλης (με χιλιάδες άτομα), έχει τόσο ελάχιστα κυματικό χαρακτήρα που είναι σχεδόν αδύνατο να τον ανιχνεύσουμε. Την εξίσωση που περιγράφει το σωματίδιο σαν κύμα (την “κυματοσυνάρτηση” όπως λέγεται) τη διατύπωσε ο Erwin Schrödinger.

Η αρχή της απροσδιοριστίας. Ας υποθέσουμε οτι θέλουμε να γνωρίζουμε ταυτόχρονα τη θέση και την ταχύτητα ενός ηλεκτρονίου. Σύμφωνα με την αρχή της απροσδιοριστίας, είναι αδύνατο να μάθουμε (με όση ακρίβεια θέλουμε) ταυτόχρονα τη θέση και την ορμή του ηλεκτρονίου — άρα και την ταχύτητά του, αφού η ταχύτητα είναι ανάλογη της ορμής. Το θέμα δεν αφορά μόνο στη θέση και ορμή (ή ταχύτητα), αλλά και σε άλλα ζευγάρια φυσικών ποσοτήτων, όπως το ενεργειακό επίπεδο ενός σωματιδίου και το χρόνο κατά τον οποίο παραμένει σ’ αυτό το ενεργειακό επίπεδο· σε κάθε περίπτωση δεν μπορούμε να γνωρίζουμε ταυτόχρονα και με όση ακρίβεια θέλουμε καί τα δύο μέλη του ζεύγους. Σύμφωνα με την κβαντική φυσική, αυτή δεν είναι απλώς μια ανθρώπινη αδυναμία, αλλά μια εγγενής ιδιότητα των υποατομικών σωματιδίων. Η αρχή της απροσδιοριστίας δηλαδή δεν οφείλεται στην τεχνολογική-μας ανικανότητα. Για να καταλάβουμε γιατί οι φυσικοί το ισχυρίζονται αυτό, ας σκεφτούμε το οτι κάθε υποατομικό σωματίδιο περιγράφεται από ένα “πακέτο κυμάτων”. Το σωματίδιο θα μπορούσε να είναι οπουδήποτε μέσα σ’ αυτό το “κυματοπακέτο”, όπου το τελευταίο υπάρχει στο χώρο. Αν θέλουμε να εντοπίσουμε όσο το δυνατόν πιο συγκεκριμένα πού είναι το σωματίδιο, θα πρέπει να “συμπιέσουμε” το κυματοπακέτο όσο το δυνατόν περισσότερο. Συμπιέζοντας όμως το κυματοπακέτο, αυξάνουμε τον αριθμό των κυμάτων που συμμετέχουν σ’ αυτό. Η ορμή του σωματιδίου (άρα και η ταχύτητα) είναι ανάλογη με το μήκος κύματος ενός από τα κύματα αυτά (κάποιου, οποιουδήποτε), άρα και ενός με μεγάλο ή μικρό μήκος κύματος. Έτσι αυξάνεται η αβεβαιότητά μας για την τιμή της ορμής (άρα και της ταχύτητας) του σωματιδίου. Την αρχή της απροσδιοριστίας (αγγλ.: uncertainty principle) διατύπωσε ο Werner Heisenberg.

Ο κβαντικός εναγκαλισμός (αγγλ.: quantum entanglement). Σωματίδια που διασπώνται, συμβαίνει να παράγουν δύο άλλα σωματίδια που έχουν αντίθετες τιμές σε κάποια ιδιότητά τους. Παραδείγματος χάρη, τα δύο παραγόμενα σωματίδια μπορεί να είναι φωτόνια, όπου το ένα φωτόνιο έχει σπιν προς μία φορά (“άνω σπιν”) και το άλλο φωτόνιο έχει σπιν προς την αντίθετη φορά (“κάτω σπιν”). Τα δύο σωματίδια φεύγουν προς αντίθετες διευθύνσεις μετά από την παραγωγή-τους. Ας υποθέσουμε οτι τα δύο φωτόνια παρήχθησαν στη Γη, και τώρα το ένα έχει φτάσει στον Άρη, ενώ το άλλο στον Ερμή. Η κβαντική φυσική λέει οτι το σπιν-τους είναι απροσδιόριστο όσο δεν έχει εξεταστεί, όπου “απροσδιόριστο” δεν σημαίνει οτι απλώς δεν το γνωρίζουμε εμείς, αλλά οτι είναι εγγενώς απροσδιόριστο, δηλαδή όντως “άνω ή κάτω”, όσο δεν εξετάζεται. Οι φυσικοί ενός εργαστηρίου στον Άρη εξετάζουν το φωτόνιο τη στιγμή που αυτό φτάνει εκεί, και βρίσκουν οτι έχει “άνω σπιν”. Σύμφωνα με την κβαντική φυσική, τη στιγμή της εξέτασης η κατάσταση του σπιν του φωτονίου “κατέπεσε”, κι από “άνω ή κάτω” που ήταν, τώρα πήρε τη συγκεκριμένη τιμή “άνω”. Τώρα, το άλλο, το “αδελφό” φωτόνιο, αυτό που τώρα έφτασε στον Ερμή, και που λέμε οτι βρίσκεται σε “εναγκαλισμό” με το πρώτο, θα πρέπει να έχει το αντίθετο σπιν από το αδελφό-του φωτόνιο, γιατί αυτό σημαίνει “εναγκαλισμός”: η τιμή της ιδιότητας του ενός εξαρτάται από την τιμή του άλλου — εδώ, τα δύο φωτόνια έχουν αντίθετο σπιν. Το παράδοξο είναι οτι τη στιγμή που έγινε η εξέταση του φωτόνιου στον Άρη και βρέθηκε οτι έχει “άνω σπιν”, θα πρέπει και το φωτόνιο στον Ερμή να “κατέπεσε” από “απροσδιόριστο σπιν” (άνω ή κάτω) σε “κάτω”, ώστε να είναι αντίθετο με αυτό του αδελφού-του. Όμως πώς έγινε αυτή η αλλαγή κατάστασης στο φωτόνιο του Ερμή; Μπορεί μια εξέταση στον Άρη να προκαλέσει ακαριαία ένα φαινόμενο στον Ερμή; Αυτή την αντίρρηση στην κβαντική φυσική διατύπωσε ο Αϊνστάιν, μέσω του περίφημου “παράδοξου EPR”, από τα αρχικά των Einstein, Podolsky, και Rosen, που διατύπωσαν το παράδοξο σε μια δημοσίευση το 1935. Ο Αϊνστάιν θεώρησε οτι είτε (1) η κβαντική φυσική πρέπει να είναι μια μη πλήρης (ατελής) θεωρία, είτε (2) αν είναι πλήρης, τότε να συμβαίνει αυτή η “μυστηριώδης δράση εξ αποστάσεως” (γερμ.: “spukhafte Fernwirkung”, όπως την ονόμασε ο Αϊνστάιν). Πειράματα που έγιναν το 1982 (και επαναλήφθηκαν αρκετές φορές από τότε) κατέληξαν στο συμπέρασμα (2), οτι δηλαδή ισχύει η “μυστηριώδης δράση εξ αποστάσεως”, άρα η κβαντική φυσική μπορεί να είναι πλήρης. Όμως “μυστηριώδεις δράσεις εξ αποστάσεως” είναι αντίθετες με το πνεύμα της φυσικής. Εννοείται οτι τα συμπεράσματα αυτά δεν θεωρούνται τελειωτικά από πολλούς φυσικούς· το μέλλον έχει πάντα τον τρόπο-του να μας εκπλήσσει.

Το φαινόμενο σήραγγας. Στο μακρόκοσμο, ένα λιοντάρι που βρίσκεται πίσω από κάγγελα παραμένει — ευτυχώς! — πίσω από τα κάγγελα χωρίς να μπορεί να επιτεθεί στους παρατηρητές που βρίσκονται από την άλλη πλευρά. Όμως στο μικρόκοσμο της κβαντικής φυσικής αυτό δεν ισχύει. Ένα υποατομικό σωματίδιο μπορεί να ξεπεράσει ένα “φράγμα” (ένα διάστημα χώρου) ακόμη και χωρίς να έχει την απαιτούμενη ενέργεια, απλά κατά τύχη. Μάλιστα το σωματίδιο βρίσκεται ακαριαία από την άλλη πλευρά του φράγματος, που σημαίνει οτι η ταχύτητα του φωτός δεν είναι αξεπέραστο εμπόδιο στο μικρόκοσμο (παρόλο που είναι στο μακρόκοσμο, όπως είδαμε στα περί θεωρίας της σχετικότητας), τουλάχιστον για εξαιρετικά μικρά χρονικά διαστήματα.

Η κίνηση ανάποδα στο χρόνο. Για κάθε είδος σωματιδίου που έχει ηλεκτρικό φορτίο υπάρχει κ’ ένα είδος “αντισωματιδίου”, που έχει ίδιο φορτίο αλλά με αντίθετο πρόσημο. Για παράδειγμα, το ηλεκτρόνιο είναι φορτισμένο αρνητικά· το αντι-ηλεκτρόνιο, ή “ποζιτρόνιο” όπως αλλιώς λέγεται, έχει όλες τις άλλες ιδιότητες του ηλεκτρονίου (π.χ. έχει σπιν = 1/2), αλλά είναι θετικά φορτισμένο με φορτίο ίσο κατ’ απόλυτη τιμή με εκείνο του ηλεκτρονίου. Για το πρωτόνιο (θετικά φορτισμένο) υπάρχει το αρνητικά φορτισμένο αντι-πρωτόνιο, κ.ο.κ. (Για σωματίδια που δεν είναι ηλεκτρικά φορτισμένα, όπως το νετρόνιο, το αντι-σωματίδιο είναι ο εαυτός-τους, όπως προκύπτει από εξισώσεις της κβαντικής φυσικής.) Αυτά τα αντισωματίδια “ζουν” για ελάχιστο χρόνο (π.χ. για εκατομμυριοστά ή δισεκατομμυριοστά του δευτερολέπτου), γιατί μόλις συναντήσουν ένα “κανονικό” (ή “συνηθισμένο”) σωματίδιο εξαϋλώνονται (μαζί με το “κανονικό” σωματίδιο) προκαλώντας έκλυση ενέργειας (π.χ. φωτόνια). Τώρα, το περίεργο είναι — όπως πρότεινε πρώτος ο φυσικός Richard Feynman (Ρίτσαρντ Φάινμαν, βλ. εικόνα) — οτι τα αντισωματίδια μπορούν να θεωρηθούν και σαν “κανονικά” σωματίδια, αλλά που ταξιδεύουν ανάποδα στο χρόνο! Δηλαδή ένα ποζιτρόνιο μπορεί να θεωρηθεί και σαν ηλεκτρόνιο το οποίο όμως “έρχεται από το μέλλον” και, αφού ταξιδέψει για πολύ μικρό χρονικό διάστημα προς τα πίσω στο χρόνο, συναντάει ένα ηλεκτρόνιο (επειδή ο κόσμος-μας βρίθει από “κανονικά” ηλεκτρόνια, που ταξιδεύουν προς την “κανονική” φορά του χρόνου), οπότε τα δυο-τους εξαϋλώνονται, δημιουργώντας (συνήθως) δύο φωτόνια υψηλής ενέργειας (ακτίνες γάμμα). Αντί λοιπόν να θεωρούμε οτι υπάρχει η “αντι-ύλη”, μπορούμε και να θεωρήσουμε οτι υπάρχει ύλη που κινείται ανάποδα στο χρόνο, της οποίας όμως απειροελάχιστες μόνο ποσότητες εμφανίζονται στον κόσμο που ζούμε. Οι δύο αυτές θεωρήσεις είναι ισοδύναμες.


Max Born Μαξ Μπορν 1882 – 1970	Wolfgang Pauli Βόλφγκανγκ Πάουλι 1900 – 1958	David Bohm Ντέιβιντ Μπομ 1917 – 1992	Richard Feynman Ρίτσαρντ Φάινμαν 1918 – 1988
Μερικοί ακόμη από τους μεγάλους φυσικούς που έπαιξαν σπουδαίο ρόλο στην πρόοδο της κβαντικής φυσικής τον 20ό αιώνα: ο Γερμανός Born, ο Αυστριακός Pauli, και οι Αμερικανοί Bohm και Feynman.

Σπουδαιότητα της κβαντικής φυσικής στην καθημερινή-μας ζωή

Μπορεί ν’ αναρωτιέται κανείς: «Ποια είναι η σημασία αυτών των ανακαλύψεων της κβαντικής φυσικής σήμερα; Γιατί ν’ αποδίδουμε τόση σπουδαιότητα σ’ αυτές τις περίεργες, “εξωπραγματικές” ανακαλύψεις; Πώς επηρεάζει η κβαντική φυσική την καθημερινότητα;»

Η απάντηση είναι οτι χωρίς τη γνώση της κβαντικής φυσικής θα ζούσαμε σήμερα σ’ έναν κόσμο πολύ “καθυστερημένο” τεχνολογικά. Δεν θα υπήρχε κανένα από τα ηλεκτρονικά αντικείμενα που σήμερα τα θεωρούμε δεδομένα από τη στιγμή που γεννιόμαστε: ούτε υπολογιστές (και φυσικά ούτε Ίντερνετ, άρα ούτε και το παρόν κείμενο), ούτε CD ή DVD, ούτε κινητά τηλέφωνα, ούτε φούρνοι μικροκυμάτων, ούτε τηλεοράσεις (ούτε καν παλιάς, αναλογικής τεχνολογίας), ούτε καν ραδιόφωνα! Ας σκεφτούμε οτι κ’ ένα ταπεινό ραδιόφωνο ακόμα (της δεκαετίας του 1970) λειτουργεί χάρη στη συσκευή που λέγεται “τρανζίστορ”, ή “ημιαγωγός” στα ελληνικά. (Μάλιστα ένα άλλο όνομα του ραδιοφώνου ήταν “το τρανζίστορ”.) Χωρίς γνώση κβαντικής φυσικής δεν μπορεί να κατασκευαστεί ένας ημιαγωγός. Πέρα όμως από τα ραδιόφωνα, ημιαγωγοί είναι και οι θεμελιώδεις μονάδες από τις οποίες φτιάχνονται αυτά που λέμε “τσιπάκια” των υπολογιστών, κινητών τηλεφώνων, και πρακτικά κάθε ηλεκτρονικής συσκευής σήμερα. Η αναλογική τηλεόραση (ας είναι και της δεκαετίας του 1960) παράγει την εικόνα με μία δέσμη ηλεκτρονίων που σαρώνει την οθόνη πολλές φορές κάθε δευτερόλεπτο. Επομένως χωρίς γνώση κβαντικής φυσικής ούτε τηλεόραση θα είχαμε. Δεν θα είχαμε συσκευές ηλεκτρονικές, αλλά μόνο ηλεκτρικές, όπως: φούρνους, κουζίνες, πλυντήρια (όχι όμως προγραμματιζόμενα με ηλεκτρονικά τσιπάκια, αλλά από τα παλιά, τα ηλεκτρικά), ψυγεία, τοστιέρες, μίξερ, κλπ. Θα είχαμε τηλέφωνα, αλλά τα αναλογικά. (Όποιος έχει προλάβει τις παλιές, αναλογικές γραμμές τηλεφώνων, γνωρίζει πόσο δύσκολη ήταν η επικοινωνία, πώς συνέβαινε να παρεμβάλλονται στην ίδια γραμμή δύο και τρεις συνδιαλέξεις, πόσο δύσκολα “έβγαινε υπεραστική γραμμή” κλπ.) Γενικά, η ζωή-μας από τεχνολογική άποψη θα βρισκόταν περίπου στη δεκαετία του 1950, και μάλιστα χωρίς να μπορεί να προοδέψει ποιοτικά παραπέρα· θα μέναμε “κολλημένοι” σ’ εκείνη την εποχή.

Γαλαξίες, και “φυγή των γαλαξιών” — η αστρονομική “ανακάλυψη του αιώνα”

Αν ρωτούσε κανείς έναν άνθρωπο μορφωμένο και άρτια ενημερωμένο των αρχών του 20^ού αιώνα, «Ως πού εκτείνεται το σύμπαν;» πιθανότατα θα έπαιρνε την απάντηση: «Μέχρι τη σφαίρα των απλανών αστέρων». Αν επέμενε κανείς ρωτώντας να μάθει ποια είναι επιτέλους τα πιο μακρυνά αστέρια, η απάντηση την εποχή εκείνη θα ήταν: «Τα αστέρια του Γαλαξία», δηλαδή της άσπρης–γαλακτερής ζώνης που βλέπουμε να εκτείνεται στον έναστρο ουρανό όταν οι συνθήκες παρατήρησης το επιτρέπουν. Ως εκεί έφτανε η γνώση των αστρονόμων μέχρι το 1925· δηλαδή πίστευαν οτι το σύμπαν είναι ο Γαλαξίας-μας. Γνώριζαν βέβαια οτι υπάρχουν και μερικές αχνά φωτισμένες περιοχές στον έναστρο ουρανό, τις οποίες ονόμαζαν “νεφελώματα”, όπως το “νεφέλωμα της Ανδρομέδας” — που φαίνεται και με γυμνό μάτι, κάτω από τον με σχήμα W αστερισμό της Κασσιόπης — αλλά δεν υποψιάζονταν οτι αυτές δεν ανήκουν στο δικό-μας Γαλαξία. Το 1925, ο Αμερικανός αστρονόμος Edwin Hubble έδειξε μέσω των παρατηρήσεών του οτι πολλά από αυτά τα “νεφελώματα” ήσαν άλλοι γαλαξίες, τελείως ξεχωριστοί από το δικό-μας, και μάλιστα κάποιοι απ’ αυτούς σε εξαιρετικά μεγάλες αποστάσεις από το δικό-μας. Ξαφνικά οι αποστάσεις στο σύμπαν μεγάλωσαν κατά περίπου μισό εκατομμύριο φορές!

Και όμως, αυτή δεν ήταν η σπουδαιότερη ανακάλυψη του Hubble. Βασιζόμενος στις προηγούμενες παρατηρήσεις-του, συμπέρανε οτι όλοι οι γαλαξίες μοιάζουν να απομακρύνονται από το δικό-μας. Μάλιστα όσο πιο μακριά είναι ένας γαλαξίας, τόσο πιο γρήγορα φαίνεται να απομακρύνεται! Αυτή, η λεγόμενη “φυγή των γαλαξιών”, αποτελεί σήμερα τον ακρογωνιαίο λίθο της κοσμολογίας, δηλαδή της επιστήμης που προσπαθεί να περιγράψει το σύμπαν στην ολότητά του, και ιδίως να κατανοήσει τη χρονική-του διάσταση, δηλαδή το από πότε υπάρχει, πώς εξελίσσεται, και πώς θα καταλήξει.

Edwin Hubble (Έντγουϊν Χάμπλ, 1889 – 1953)

Το οτι νεφελώματα όπως αυτό της Ανδρομέδας είναι στην πραγματικότητα γαλαξίες, ο Hubble το συμπέρανε ως εξής. Υπάρχει ένας τύπος αστέρων που ονομάζονται “Κηφείδες” (από τον πιο χαρακτηριστικό εκπρόσωπό τους, τον αστέρα δέλτα του αστερισμού του Κηφέως), οι οποίοι έχουν μεταβλητή φωτεινότητα. Η φωτεινότητά τους μεταβάλλεται καθώς πάλλονται. Αλλά όσο πιο μεγάλη είναι η μέση φωτεινότητά τους, τόσο πιο γρήγορα πάλλονται, και η σχέση μεταξύ μέσης φωτεινότητας και περιόδου με την οποία πάλλονται είναι συγκεκριμένη και γνωστή. Οπότε μετρώντας την περίοδο ενός Κηφείδα και το πόσο φωτεινός φαίνεται από τη Γη, μπορούμε να βρούμε την πραγματική-του φωτεινότητα (το “απόλυτο μέγεθός του”, όπως λέγεται), άρα και το πόσο μακριά βρίσκεται. Αυτό έκανε κι ο Hubble, που υπολόγισε το πόσο μακριά είναι κάποιοι Κηφείδες που βρίσκονται μέσα σ’ αυτά που τότε ονόμαζαν “νεφελώματα” — δηλαδή σε γαλαξίες. Βρίσκοντας την απόσταση των Κηφείδων, ουσιαστικά βρήκε την απόσταση των γαλαξιών. Σήμερα, για να μετρήσουμε αποστάσεις που είναι τόσο μεγάλες ώστε να αποκλείουν την παρατήρηση Κηφείδων αστέρων μέσα στους γαλαξίες, χρησιμοποιούμε τους αστέρες που εκκρήγνυνται σαν υπερκαινοφανείς (σουπερνόβα) τύπου Ιa. Η ιδέα όμως είναι η ίδια.

Σμήνος γαλαξιών σε μια περιοχή του ουρανού. Ο δικός-μας Γαλαξίας
θα έμοιαζε με έναν απ’ αυτούς αν μπορούσαμε να τον δούμε από μακριά.
(Τα μεμονωμένα αστέρια, όπως αυτό κοντά στο κέντρο, ανήκουν στο δικό-μας Γαλαξία.)

Από κει και πέρα ήταν θέμα χρόνου για τον Hubble να παρατηρήσει και τη “φυγή των γαλαξιών”. Όταν ένας αστέρας κινείται προς εμάς, το φως-του μετατοπίζεται ελαφρά προς το κυανό τμήμα του ηλεκτρομαγνητικού φάσματος. Αντίθετα, όταν απομακρύνεται από μας, το φως-του μετατοπίζεται ελαφρά προς το ερυθρό τμήμα του φάσματος. Όσο πιο μεγάλη είναι η ταχύτητα του αστέρα (από ή προς εμάς), τόσο πιο μεγάλη είναι η μετατόπιση στο φάσμα του φωτός-του. Ο Hubble βρήκε οτι το φως των αστέρων των γαλαξιών εκείνων που βρίσκονται πιο μακριά από τη δική-μας “τοπική ομάδα” γαλαξιών (που περιλαμβάνει και αυτόν της Ανδρομέδας) είναι μετατοπισμένο προς το ερυθρό, που σημαίνει οτι σχεδόν όλοι οι γαλαξίες απομακρύνονται από εμάς. Και μάλιστα, βρήκε ένα ακόμα πιο εντυπωσιακό αποτέλεσμα: όσο πιο μακριά είναι ο γαλαξίας, τόσο πιο γρήγορα απομακρύνεται από εμάς! Αυτό το λέμε σήμερα “νόμο του Hubble”:

Νόμος του Hubble:
Η ταχύτητα με την οποία οι γαλαξίες απομακρύνονται από το δικό-μας Γαλαξία είναι ανάλογη της απόστασής τους από μας.

Πώς εξηγούνται τα παραπάνω; Μήπως το οτι οι γαλαξίες απομακρύνονται από μας σημαίνει οτι είμαστε στο κέντρο του σύμπαντος;

Όχι βέβαια. Για να καταλάβουμε πώς συμβαίνει να μας φαίνεται σαν οι γαλαξίες να φεύγουν από μας χωρίς να είμαστε στο κέντρο του σύμπαντος, μπορούμε με τη φαντασία-μας να μειώσουμε τις διαστάσεις του σύμπαντος. Ας φανταστούμε το σύμπαν να είναι σαν την επιφάνεια ενός μπαλονιού (άρα να έχει δύο διαστάσεις), και τους γαλαξίες να είναι κουκκίδες ζωγραφισμένες με μαρκαδόρο πάνω στο μπαλόνι. Τί θα συμβεί αν αρχίσουμε να φουσκώνουμε το μπαλόνι; Οι κουκκίδες θ’ αρχίσουν να απομακρύνονται η μία από την άλλη. Αν υποθέσουμε πως είμαστε σε μία από εκείνες τις κουκκίδες, καθώς το μπαλόνι θα φουσκώνει, θα μας φαίνεται οτι κάθε κουκκίδα απομακρύνεται από εμάς· και μάλιστα, όσο πιο μακριά είναι η κουκκίδα, τόσο πιο γρήγορα θα μοιάζει να απομακρύνεται (υποθέτοντας οτι βλέπουμε μόνο πάνω στην επιφάνεια του μπαλονιού, και όχι διαμέσου-του· δηλαδή υποθέτοντας οτι το φως διαδίδεται μόνο πάνω στην επιφάνεια του μπαλονιού). Αυτό το οποίο συμβαίνει στις κουκκίδες του μπαλονιού σε δύο διαστάσεις, είναι ανάλογο αυτού που συμβαίνει στους γαλαξίες του σύμπαντος σε τρεις διαστάσεις. Άρα ο χώρος του σύμπαντος διαστέλλεται.

Εφόσον λοιπόν οι γαλαξίες απομακρύνονται ο ένας από τον άλλον, έπεται οτι κάποια χρονική στιγμή θα έπρεπε να ήσαν όλοι πολύ κοντά ο ένας στον άλλον. Ή, για να το πούμε ακριβέστερα, έπεται οτι η ύλη του σύμπαντος θα έπρεπε να ήταν συγκεντρωμένη σε έναν πολύ μικρό χώρο. Αυτή η υπόθεση, που έχει πλέον επιβεβαιωθεί από άλλες, ανεξάρτητες παρατηρήσεις, ονομάζεται “Θεωρία της Μεγάλης Έκκρηξης” (αγγλ.: Big Bang Theory), και αποτελεί σήμερα μια υπόθεση πάνω στην οποία στηρίζονται πρακτικά όλα τα κοσμολογικά μοντέλα του σύμπαντος (με ελάχιστες εξαιρέσεις).

Τα όρια της λογικής

Οι προηγούμενες δύο ενότητες είχαν κατά κάποιο τρόπο σχέση με τα όρια της φυσιολογίας του ανθρώπου: η μεν φυσική έφτασε να περιγράφει οντότητες όπως τα υποατομικά σωματίδια, που βρίσκονται στο όριο αυτού που είναι άμεσα παρατηρήσιμο από τον ανθρώπινο εγκέφαλο· η δε αστρονομία έφτασε να περιγράφει όλα όσα μπορούν να παρατηρηθούν στο μακρόκοσμο, καθώς η πληροφορία σχετικά με το σύμπαν μας παρέχεται μέσω του φωτός (ή γενικότερα μέσω της ηλεκτρομαγνητικής ακτινοβολίας), και από ένα σημείο του σύμπαντος και πέρα η πληροφορία δεν φτάνει πια σ’ εμάς γιατί η απόσταση είναι τόσο μεγάλη που το φως δεν έχει προλάβει να τη διανύσει. (Και ούτε πρόκειται ποτέ να τη διανύσει γιατί ο χώρος διαστέλλεται, κάνοντας όλο και μεγαλύτερο το ταξίδι του φωτός στο χώρο.)

Η παρούσα ενότητα έχει να κάνει με τα λογικά όρια του ανθρώπινου νου. Εδώ θα συναντήσουμε την ανακάλυψη οτι ούτε εμείς ούτε καμιά μηχανή μπορεί ποτέ να συμπεράνει με λογικό τρόπο όλα όσα είναι αληθινά στον κόσμο.

Από τα τέλη του 19^ου μέχρι και το πρώτο τέταρτο του 20^ού αιώνα ένα μεγαλεπίβολο σχέδιο καταστρώθηκε στους νους των σπουδαίων μαθηματικών της εποχής εκείνης: ήθελαν να μπορέσουν να φτιάξουν ένα σύνολο αξιωμάτων (αρχικών υποθέσεων) βάσει των οποίων να μπορεί ν’ αποδειχτεί με μηχανικό τρόπο οποιαδήποτε αληθινή πρόταση των μαθηματικών. Παράδειγμα: ας υποθέσουμε οτι η πρόταση «Κάθε ζυγός αριθμός που είναι μεγαλύτερος του 2 μπορεί να γραφεί σαν άθροισμα δύο πρώτων αριθμών» είναι αληθινή. Οι μαθηματικοί έλπιζαν να βρουν ένα σύνολο αξιωμάτων από το οποίο να μπορούν να συνάγουν όχι μόνο την παραπάνω πρόταση, αλλά και κάθε άλλη αληθινή πρόταση. Αυτή η επιθυμία-τους δημιουργήθηκε γιατί τα μαθηματικά περνούσαν μια περίοδο κρίσης: είχαν βρεθεί κάποια μαθηματικά παράδοξα (δηλαδή προτάσεις που ήσαν καί σωστές καί λάθος), οπότε οι μαθηματικοί αισθάνονταν οτι έπρεπε να βάλουν το αντικείμενο της μελέτης-τους σε μια στέρεη βάση — από λογική άποψη — ώστε να εξαλειφθούν τα παράδοξα.

Το θέμα έχει φιλοσοφικές προεκτάσεις που ξεπερνούν το στενό πεδίο των μαθηματικών. Φιλόσοφοι–μαθηματικοί όπως ο Bertrand Russell (Μπέρτραντ Ράσελ, 1872 – 1970) ήθελαν να δώσουν απόλυτη ισχύ στον ορθολογικό τρόπο σκέψης. Σκέφτονταν λοιπόν οτι αν π.χ. ήταν δυνατό να εκφράσουμε με μαθηματικό–λογικό τρόπο την ανθρώπινη γνώση για τον κόσμο που μας περιβάλλει, ίσως θα μπορούσαμε να βρούμε ένα σύνολο αξιωμάτων βάσει του οποίου να συμπεράνουμε οτιδήποτε είναι σωστό για τον κόσμο-μας. Αυτό το σύνολο αξιωμάτων θα ήταν τότε το θεμέλιο πάνω στο οποίο θα στηριζόταν όλη η ανθρώπινη γνώση για το τί είναι σωστό και τί λάθος. Αν είχαμε μια απορία για το αν κάτι είναι αληθινό ή όχι, θα μπορούσαμε ίσως να ζητήσουμε από μια μηχανή (ένα σύγχρονο “μαντείο”) να ξεκινήσει από τα θεμελιώδη αξιώματα της γνώσης, κι αφού δουλέψει μ’ αυτά για λίγη ώρα να μας δώσει μια απάντηση: «Ναι, αυτό που ρωτάτε ισχύει, είναι αληθινό», ή: «Όχι, αυτό που ρωτάτε δεν ισχύει». Θα μπορούσε ποτέ να υπάρξει ένα τέτοιο Απόλυτο Μαντείο στη νέα, ορθολογική εποχή του Russell; Μήπως θα μπορούσαμε να έχουμε ένα τέτοιο Μαντείο στο μέλλον;

Η απάντηση δόθηκε το 1931 από τον Αυστριακό μαθηματικό Kurt Gödel, και ήταν αρνητική.

Kurt Gödel (Κουρτ Γκέντελ, 1906 – 1978), και η μη πληρότητα της αριθμητικής

Ήδη από το 1931, όταν ήταν ακόμη στη Βιέννη, ο Gödel είχε δημοσιεύσει την απόδειξη του θεωρήματος της “μη πληρότητας της αριθμητικής”. Το θεώρημα αυτό λέει το εξής:

Θεώρημα του Gödel, περί “μη πληρότητας της αριθμητικής”:
Για κάθε θεωρία η οποία βασίζεται σε ένα σύνολο αξιωμάτων που είναι αρκετά ισχυρά ώστε να θεμελιώσουν την αριθμητική, υπάρχει τουλάχιστον μία αληθινή πρόταση της αριθμητικής που όμως η αλήθεια-της δεν μπορεί να αποδειχτεί από αυτό το σύνολο των αξιωμάτων.

Δηλαδή: ας πούμε οτι έχουμε τα αξιώματα Α₁, Α₂, ...κλπ, έως Α_κ, που είναι αρκετά ώστε πάνω-τους να μπορούμε να θεμελιώσουμε την οικεία-μας θεωρία της αριθμητικής. Από αυτά τα αξιώματα συμπεραίνουμε ένα μεγάλο αριθμό από θεωρήματα, π.χ. τις προτάσεις Β₁, Β₂, ..., έως Β_λ. Όλα αυτά τα θεωρήματα γνωρίζουμε οτι είναι σωστά, δηλαδή αληθινές προτάσεις, αφού αποδείχτηκαν από τα αξιώματα. Το θεώρημα μη πληρότητας του Gödel λέει οτι τότε θα υπάρχει μια πρόταση Γ η οποία θα είναι μεν αληθινή, αλλά που δεν θα μπορεί ν’ αποδειχτεί από τις προτάσεις της θεωρίας, δηλαδή από τα Α₁, Α₂, ..., Α_κ, Β₁, Β₂, ..., Β_λ. Πάντα θα υπάρχει τουλάχιστον μία αλήθεια που θα “ξεφεύγει” από τη θεωρία, καθώς θα μένει αναπόδεικτη.

Ο Gödel απέδειξε το παραπάνω θεώρημα με έναν εξαιρετικά ευρηματικό, αλλά απλό στην κατανόηση τρόπο, τον εξής: ουσιαστικά χρησιμοποίησε την αριθμητική, τους αριθμούς δηλαδή, σαν ένα σύστημα κωδικοποίησης, μέσω του οποίου μπορούσε να κωδικοποιεί προτάσεις της αριθμητικής. Αφού το έκανε αυτό, κωδικοποίησε μέσω του συστήματός του την εξής πρόταση:

Ας ονομάσουμε G την παραπάνω πρόταση, που μέσω της κωδικοποίησης του Gödel είναι κι αυτή μια πρόταση της αριθμητικής.

Ας υποθέσουμε τώρα οτι το θεώρημα μη πληρότητας δεν ισχύει, δηλαδή υποθέτουμε οτι όλες οι αληθινές προτάσεις της αριθμητικής μπορούν ν’ αποδειχτούν. Είναι η G αλήθεια ή ψέμα; Αν είναι αλήθεια, τότε — σαν αληθινή πρόταση της αριθμητικής — μπορεί ν’ αποδειχτεί. Αλλά αφού είναι αλήθεια αυτό που λέει, βγάζουμε το συμπέρασμα οτι δεν μπορεί ν’ αποδειχτεί. Αλλά αφού δεν μπορεί ν’ αποδειχτεί, πάει να πει οτι είναι ψέμα, γιατί αν ήταν αλήθεια θα μπορούσε ν’ αποδειχτεί. Καταλήγουμε έτσι στο συμπέρασμα οτι η G είναι καί ψέμα, καί αλήθεια — πράγμα άτοπο. Άρα η αρχική-μας υπόθεση οτι το θεώρημα μη πληρότητας δεν ισχύει ήταν λάθος. Άρα το θεώρημα μη πληρότητας ισχύει.

Σπουδαιότητα του θεωρήματος μη πληρότητας

Με μια επιφανειακή επισκόπηση των παραπάνω μπορεί κανείς να μείνει με την εντύπωση: «Ε, και λοιπόν; Γιατί είναι σπουδαίο το οτι θα υπάρχουν πάντα αληθινές προτάσεις στην αριθμητική που δεν θα μπορούν ν’ αποδειχτούν από ένα δοσμένο σύνολο αξιωμάτων;»

Το ζήτημα είναι οτι η αριθμητική είναι μια αρκετά απλή μαθηματική θεωρία. Αν αυτό το πρόβλημα το έχει η αριθμητική, έπεται οτι θα το έχει και κάθε άλλη θεωρία που είναι πιο πολύπλοκη από την αριθμητική — δηλαδή πρακτικά κάθε ενδιαφέρουσα θεωρία. Και ενδιαφέρουσες θεωρίες είναι όχι μόνο αυτές των μαθηματικών, αλλά και άλλες, λογικές θεωρίες που εφαρμόζουν στον κόσμο στον οποίο ζούμε. Με άλλα λόγια, το πρόβλημα της μη πληρότητας το έχει όχι απλά η αριθμητική, αλλά η λογική. Το όνειρο του Russell, που ήταν να χτιστεί ένα στέρεο βάθρο υποθέσεων ώστε μέσω της ορθολογικής σκέψης να μπορεί να απαντηθεί σαν σωστή ή λάθος οποιαδήποτε πρόταση, κατέρρευσε. Εξίσου βέβαια κατέρρευσε και το όνειρο των άλλων μαθηματικών, που ήταν να βάλουν μια για πάντα τα μαθηματικά σε στέρεη, αναλλοίωτη βάση. Τέτοια βάση δεν υπάρχει, όπως απέδειξε ο Gödel.

Το θεώρημα μη πληρότητας του Gödel σημαίνει οτι καμιά μηχανή δεν μπορεί ποτέ να συμπεράνει με λογικό τρόπο όλα όσα είναι αληθινά στον κόσμο. Αρχικά, και για ένα μεγάλο μέρος του 20^ού αιώνα, αυτό ερμηνεύτηκε ως το εξής “χαρμόσυνο μήνυμα”: καμιά μηχανή δεν μπορεί να το κάνει αυτό· άρα εμείς οι άνθρωποι, που είμαστε υπεράνω των μηχανών, μπορούμε να κάνουμε περισσότερα — π.χ. να “ξεφύγουμε” από τις αρχικές-μας υποθέσεις και ν’ αποδείξουμε τη ζητούμενη πρόταση με άλλο, ευφυή τρόπο.

Είναι όμως σωστό το ότι είμαστε “υπεράνω των μηχανών”, δηλαδή των υπολογιστών; Όποιος δεν γνωρίζει αρκετά από τη θεωρία υπολογισμού και από τη νευροβιολογία του εγκεφάλου, μπορεί να πιστεύει αυτό το πράγμα. Όταν όμως μελετούμε τη λειτουργία του εγκεφάλου βλέπουμε οτι αυτός είναι καθαρά μία μηχανή — απλώς με διαφορετική αρχιτεκτονική από τους υπολογιστές του σήμερα. Άλλες γνώσεις από την επιστήμη της νοολογίας μας υποδεικνύουν οτι ο νους του ανθρώπου είναι αποκλειστικά το αποτέλεσμα της λειτουργίας του εγκεφάλου. Ο νους-μας δηλαδή, παρόλο που επιφανειακά μοιάζει να είναι “κάτι παραπάνω από μηχανή”, στην πραγματικότητα δεν είναι παρά μια (“αναφυόμενη”) ιδιότητα μιας σύνθετης μηχανής: του εγκεφάλου. Τα όρια των μηχανών είναι και όρια του εγκεφάλου. Συνεπώς, τα όρια της λογικής των μηχανών μάλλον είναι και όρια του νου του ανθρώπου. Αυτό είναι προς το παρόν το — όχι επιστημονικό, αλλά φιλοσοφικό — συμπέρασμα από το θεώρημα του Gödel.

Το δραματικό τέλος του 2^ου Παγκοσμίου Πολέμου

Όπως όμως λέει ένα αρχαίο ρητό, “ουδέν κακόν αμιγές καλού” (στην αισιόδοξή του έκδοση). Ο 2^ος Παγκόσμιος Πόλεμος έδωσε εξ ανάγκης μια πρωτόγνωρη ώθηση στην επιστημονική έρευνα, αποτέλεσμα της οποίας ήταν μια χωρίς προηγούμενο ανάπτυξη της τεχνολογίας. Ίσως ούτε οι υπολογιστές θα εμφανίζονταν και εξελίσσονταν τόσο γρήγορα, ούτε πολλές από τις άλλες ηλεκτρονικές συσκευές που σήμερα βρίσκονται παντού γύρω-μας θα υπήρχαν.

Η αυγή των υπολογιστών

Κοιτάζοντας τον τεχνολογικό κόσμο με τον οποίο η ζωή-μας είναι σήμερα άρρηκτα δεμένη, μπορεί να μας δημιουργηθεί η εντύπωση οτι διάφορες συσκευές, όπως κινητά τηλέφωνα, ψηφιακές τηλεοράσεις, υπολογιστές, συσκευές αναπαραγωγής ήχου (π.χ. MP3, CD), ή εικόνας (π.χ. DVD), ψηφιακές κάμερες, κ.ά., ανήκουν όλες σε μια κατηγορία: τις “συσκευές υψηλής τεχνολογίας”, αυτές που τις βρίσκουμε συγκεντρωμένες στο τμήμα ηλεκτρονικών ενός πολυκαταστήματος. Και όμως, ανάμεσα σε όλα αυτά τα “ηλεκτρονικά” υπάρχει ένα είδος που είναι ποιοτικά διαφορετικό από οτιδήποτε άλλο έχει υπάρξει μέχρι στιγμής στον πλανήτη, με την εξαίρεση μόνο του ανθρώπινου εγκεφάλου. Το είδος αυτό είναι οι υπολογιστές. Μπορούμε να υποπτευθούμε οτι “κάτι το ιδιαίτερο ισχύει” για τους υπολογιστές αν σκεφτούμε οτι ένας υπολογιστής μπορεί να μιμηθεί τη λειτουργία μιας τηλεόρασης, ενός DVD, μιας κάμερας, ενός ραδιοφώνου, ή μιας οποιασδήποτε άλλης συσκευής, αρκεί να τον προγραμματίσουμε κατάλληλα. Αντίθετα, καμία τηλεόραση δεν μπορεί να μιμηθεί τη λειτουργία ενός υπολογιστή. Το θέμα όμως είναι βαθύτερο. Πολλοί επιστήμονες της εποχής-μας οι οποίοι εργάζονται σε τομείς σχετικούς με υπολογιστές (τεχνητή νοημοσύνη, νοολογία, γνωσιακή ψυχολογία) πιστεύουν οτι οι υπολογιστές μπορούν να μιμηθούν και τη λειτουργία του ανθρώπινου εγκεφάλου· απλώς δεν ξέρουμε ακόμα πώς να τους προγραμματίσουμε ώστε να πετύχουμε κάτι τέτοιο. Αν αυτό είναι σωστό, τότε οι υπολογιστές, όπως και οι ανθρώπινοι εγκέφαλοι, ανήκουν σε μια ιδιαίτερη κατηγορία οντοτήτων στο σύμπαν: των οντοτήτων που υπολογίζουν. Και μάλιστα υπολογίζουν όχι με έναν οποιονδήποτε τρόπο, γιατί μπορεί να υποτεθεί οτι υπολογίζει και μια αριθμομηχανή τσέπης, ή ο εγκέφαλος ενός πιθήκου. Οι οντότητες αυτές λέμε οτι «έχουν την υπολογιστική ισχύ μιας “Μηχανής Τούρινγκ”», την οποία θα γνωρίσουμε στη συνέχεια. Αντίθετα, καμία άλλη οντότητα, όπως αριθμομηχανές τσέπης (εκτός από τις προγραμματιζόμενες), κινητά τηλέφωνα, τηλεοράσεις, ή εγκέφαλοι άλλων ζώων, δεν έχει την υπολογιστική ισχύ μιας Μηχανής Τούρινγκ.

Από τα παραπάνω έπεται οτι μπορούμε να αποφύγουμε και μία ακόμη παρανόηση. Μπορεί οι υπολογιστές να μας φαίνονται πολύ διαφορετικοί μεταξύ-τους. Υπάρχουν υπολογιστές επιτραπέζιοι και laptop, ή τώρα πλέον και μεγέθους παλάμης· υπάρχουν άλλοι που βρίσκονται σε πανεπιστήμια και ερευνητικά κέντρα, υπερυπολογιστές, κλπ., που τους αφιερώνεται μια ολόκληρη αίθουσα για τις συσκευές-τους· υπάρχουν πολλές μάρκες υπολογιστών· κάποιοι που τους λέμε “συμβατούς με PC” (ή απλά PC), και άλλοι της εταιρείας Apple. Παρ’ όλη αυτή τη φαινομενική πολυπλοκότητα, η ουσία είναι οτι όλοι οι υπολογιστές — όχι μόνο αυτοί που έχουμε σήμερα, αλλά κι αυτοί που θα κατασκευάσουμε στο άμεσο μέλλον — είναι ενός τύπου: του τύπου που περιγράφεται μαθηματικά από το υπολογιστικό μοντέλο της Μηχανής Τούρινγκ, που προτάθηκε γύρω στο 1936 από τον θεωρούμενο σήμερα “πατέρα της επιστήμης υπολογιστών”, το Βρετανό Άλαν Μάθισον Τούρινγκ.

Alan Turing (Άλαν Τούρινγκ, 1912 – 1954)

Στη δημοσίευση αυτή εισήγαγε αυτό που αργότερα ονομάστηκε “Μηχανή Τούρινγκ”: ένα μαθηματικό μοντέλο που θεωρούμε σήμερα σαν το “απόσταγμα” της έννοιας “υπολογιστής”. Με τί μοιάζει όμως μια Μηχανή Τούρινγκ;

Βασικό μοντέλο Μηχανής Τούρινγκ, με ταινία άπειρη προς μία διεύθυνση, και αλφάβητο ενός μόνο συμβόλου

Όπως δείχνει το παραπάνω διάγραμμα, μια Μηχανή Τούρινγκ διαθέτει μια ταινία που αποτελείται από κελλιά. Μέσα στο κάθε κελλί μπορεί να γραφεί ένα σύμβολο από ένα “αλφάβητο” (στο παράδειγμά μας, το αλφάβητο περιλαμβάνει ένα μόνο σύμβολο: το “1”)· ή μπορεί το κελλί να είναι κενό. Η ταινία είναι ατέρμονη προς τη μία διεύθυνση, δηλαδή περιλαμβάνει άπειρο αριθμό κελλιών. Πάντως μόνο ένα περιορισμένο πλήθος κελλιών μπορεί να έχει σύμβολα από το αλφάβητο· όλα τα υπόλοιπα κελλιά, δεξιά του τελευταίου συμβόλου, πρέπει να είναι κενά. Η μηχανή έχει επίσης μια “κεφαλή”, η οποία ανά πάσα στιγμή “βλέπει” ένα μόνο κελλί, και μπορεί είτε να γράψει ένα σύμβολο του αλφαβήτου μέσα στο κελλί αυτό, είτε να το σβήσει (να κάνει το κελλί κενό)· ταυτόχρονα, η κεφαλή μπορεί να μετακινηθεί δεξιά, ή αριστερά, ή να μείνει στη θέση-της. Φυσικά δεν μπορεί να πάει πιο αριστερά από το αριστερό άκρο της ταινίας. Το τί ακριβώς θα κάνει η κεφαλή εξαρτάται από ένα “πρόγραμμα” που διαθέτει, που της δίνει απλούστατες εντολές του τύπου: «Αν δεις το σύμβολο 1 στο κελλί και είσαι στην κατάσταση Α, τότε κάνε το κελλί κενό, μετακινήσου μία θέση δεξιά, και να είσαι τώρα στην κατάσταση Β.» Μια σειρά από τέτοιες “εντολές” είναι όλο το πρόγραμμα της Μηχανής Τούρινγκ. Αρχικά της δίνεται μια ταινία με ορισμένα σύμβολα μέσα στα κελλιά-της (αυτό είναι το “input”, το αρχικό δεδομένο της μηχανής). Η μηχανή ξεκινάει, ακολουθεί τις εντολές του προγράμματός της, και όταν τελειώσει (αν ποτέ τελειώσει) αφήνει την ταινία με κάποια σύμβολα στα κελλιά-της (αυτό είναι το “output”, το τελικό αποτέλεσμα της μηχανής).

Όπως βλέπουμε, πρόκειται για έναν απλούστατο υπολογιστή. Αυτός όμως ο υπολογιστής, παρά την απλότητά του, αποδεικνύεται οτι μπορεί να μιμηθεί οποιονδήποτε σημερινό υπολογιστή — τόσο αυτόν με τον οποίο διαβάζετε το παρόν κείμενο, όσο και έναν από τους υπερυπολογιστές που διαθέτουν μόνο ορισμένα ιδρύματα ή πανεπιστήμια στον κόσμο. Η “μίμηση” είναι με την εξής έννοια: δεν υπάρχει καμία μαθηματική λειτουργία που να μπορεί να κάνει ένας υπολογιστής, και που να μην μπορεί να την κάνει και μια Μηχανή Τούρινγκ (Μ.Τ.). Δηλαδή ότι μπορεί να υπολογίσει ένας σημερινός υπολογιστής, μπορεί να το υπολογίσει και μια Μ.Τ. Το αντίθετο μάλιστα συμβαίνει: υπάρχουν κάποιες σπάνιες μαθηματικές λειτουργίες που μπορεί να υπολογίσει η Μ.Τ. αλλά που είναι εκτός των δυνατοτήτων ακόμα και των σημερινών υπερυπολογιστών. (Αυτό συμβαίνει γιατί η Μ.Τ. έχει ταινία — δηλαδή μνήμη — που είναι άπειρη, ενώ ένας υπολογιστής έχει κατ’ ανάγκη πεπερασμένη μνήμη.) Υπόψη οτι όταν λέμε “μαθηματικές λειτουργίες” εννοούμε “οτιδήποτε υπολογίζεται”· δηλαδή και το Word, ή το Excel, ή οποιοδήποτε πρόγραμμα, εκτελούν μαθηματικές λειτουργίες και τίποτα άλλο, στην πραγματικότητα.

Μέσω της Μηχανής Τούρινγκ μπορούμε να μελετήσουμε τις ιδιότητες των υπολογιστών, και να χτίσουμε μια “θεωρία υπολογισμού”, που είναι το πιο θεμελιώδες μάθημα της επιστήμης υπολογιστών. Υπάρχουν και άλλα μαθηματικά μοντέλα που έχουν προταθεί, κανένα όμως δεν έχει την αμεσότητα της Μ.Τ. Επίσης, καθένα από τα άλλα μοντέλα έχει αποδειχτεί οτι είναι ισοδύναμο σε υπολογιστική ικανότητα με τη Μ.Τ. Αυτή η αδυναμία να βρεθεί κάποιο υπολογιστικό μοντέλο που να μπορεί να υπολογίσει κάτι περισσότερο από τη Μ.Τ., οδήγησε τον Τούρινγκ και τον επιβλέποντα καθηγητή-του Alonzo Church (Αλόνζο Τσερτς, 1903 – 1995) στο να διατυπώσουν την περίφημη “θέση Τσερτς–Τούρινγκ” (αγγλ.: “Church–Turing thesis”):

Θέση Τσερτς–Τούρινγκ:
Οτιδήποτε υπολογίζεται, μπορεί να υπολογιστεί από μια Μηχανή Τούρινγκ.

Το παραπάνω ονομάζεται “θέση” (ή υπόθεση, ή τοποθέτηση) και όχι “θεώρημα” γιατί δεν μπορεί να αποδειχτεί μαθηματικά, καθώς δεν είναι δυνατό να εκφράσουμε με μαθηματικό τρόπο την έννοια “οτιδήποτε υπολογίζεται”. Είναι όμως μια σημαντική ιδέα, γιατί αν κάνουμε τη λογική υπόθεση οτι και οι νευρώνες του ανθρώπινου εγκεφάλου κάνουν υπολογισμούς — όπως συμπεραίνεται από την εξέτασή τους μέσω της επιστήμης της νευροβιολογίας — τότε και η λειτουργία του ανθρώπινου εγκεφάλου μπορεί — κατ’ αρχήν, δηλαδή θεωρητικά, όχι στην πράξη — να προσομοιωθεί από μια Μηχανή Τούρινγκ.

Κατά τη διάρκεια του 2^ου Παγκοσμίου Πολέμου ο Τούρινγκ βοήθησε τη χώρα-του στην αποκρυπτογράφηση Γερμανικών μηνυμάτων, που κωδικοποιούνταν τότε μέσω της συσκευής Enigma (Αίνιγμα). Ο Τούρινγκ επινόησε μια μέθοδο μέσω της οποίας τα μηνύματα μπορούσαν να αποκωδικοποιηθούν σε ένα πολύ μικρό κλάσμα του χρόνου από αυτό που θα χρειαζόταν χωρίς τη μέθοδό του. Σύμφωνα με κάποιους υπολογισμούς, η αποκρυπτογράφηση των Γερμανικών μηνυμάτων από τις συμμαχικές δυνάμεις επιτάχυνε τη νίκη των τελευταίων κατά δύο χρόνια.

Δυστυχώς η χώρα-του δεν του ανταπέδωσε ποτέ τα όσα εκείνος προσέφερε. Το 1952 ο Τούρινγκ δικάστηκε με την κατηγορία της ομοφυλοφυλίας, που τότε ήταν αδίκημα στη Βρετανία. Του δόθηκε η επιλογή, είτε να φυλακιστεί, είτε να υποστεί χημική θεραπεία με ορμόνες (οιστρογόνα) που θα του μείωναν τη σεξουαλική δραστηριότητα. Επέλεξε το δεύτερο, που όμως είχε παρενέργειες, όπως την ανάπτυξη στήθους. Τον Ιούνιο του 1954 ο Τούρινγκ βρέθηκε νεκρός στο δωμάτιό του, και από τη νεκροψία διαπιστώθηκε οτι αυτοκτόνησε καταπίνοντας κυάνιο.

Ενδιαφέρον είναι να σημειώσουμε το οτι τόσο οι πρώτοι υπολογιστές (όπως ο ENIAC, φωτ. αριστερά, που είχαν μέγεθος δωματίου, αλλά υπολογιστική ισχύ μηδαμινή συγκριτικά με τον προσωπικό υπολογιστή που χρησιμοποιείτε σήμερα για να διαβάσετε το παρόν κείμενο), όσο και οι σημερινοί υπολογιστές, ανεξαρτήτως μάρκας, μεγέθους, ή χρόνου κατασκευής, ακολουθούν την αρχιτεκτονική von Neumann. Μπορεί δηλαδή να νομίζουμε οτι αγοράζουμε διαφορετικό υπολογιστή κάθε φορά, αλλά στην πραγματικότητα αυτό που κάνουμε είναι οτι αγοράζουμε μια παραλλαγή της υπολογιστικής αρχιτεκτονικής του von Neumann. Υπολογιστές με διαφορετική αρχιτεκτονική υπάρχουν μεν, αλλά βρίσκονται σε ερευνητικά ιδρύματα, όχι στα ράφια των καταστημάτων.

Ανακάλυψη της δομής του DNA

Από τα μέσα του 19^ου αιώνα είχε να πραγματοποιηθεί ένα μεγάλο βήμα στη βιολογία· συγκεκριμένα από το 1859, όταν διατυπώθηκε από τον Charles Darwin ο τρόπος με τον οποίο τα έμβια όντα εξελίσσονται (μέσω του μηχανισμού της φυσικής επιλογής). Σχεδόν έναν αιώνα αργοτερα, το 1953, έγινε το δεύτερο μεγάλο βήμα, όταν αποκρυπτογραφήθηκε η δομή του μορίου του DNA.

Ήταν ήδη γνωστό από τον προηγούμενο αιώνα οτι οι οργανισμοί κληρονομούν από τους προγόνους-τους ορισμένα χαρακτηριστικά. Επίσης ήταν γνωστό οτι αυτή η κληρονομικότητα των γενετικών χαρακτηριστικών βρισκόταν στη βάση του μηχανισμού της εξέλιξης. Αυτό που δεν ήταν ακόμα όμως γνωστό ήταν με ποιον τρόπο ακριβώς κληρονομούνταν τα γενετικά χαρακτηριστικά.

Επίσης, και το DNA ήταν ήδη γνωστό από τον προηγούμενο αιώνα, αλλά τότε ακόμα δεν υπήρχε καν η υποψία οτι αυτό το “οξύ” ήταν υπεύθυνο για την κληρονομική μεταβίβαση των χαρακτηριστικών από πρόγονο σε απόγονο. Η ιστορία εξακρίβωσης του ρόλου του DNA και της ανακάλυψης της δομής-του ακολούθησε τα παρακάτω στάδια:


Rosalind Franklin Ρόζαλιντ Φράνκλιν 1920 – 1958	Raymond Gosling Ρέυμοντ Γκόσλιγκ 1926 – 2015	James D. Watson Τζέιμς Γουάτσον 1928 –	Francis Crick Φράνσις Κρικ 1916 – 2004
Μερικοί από τους πολλούς επιστήμονες που συνεισέφεραν στην κατανόηση του τρόπου με τον οποίο δομείται το μόριο του DNA

Το DNA είναι αρκτικόλεξο που σημαίνει στα αγγλικά: deoxyribonucleic acid, το οποίο στα ελληνικά έχει μεταφερθεί με δύο τρόπους: είτε σαν το παλιότερο δεσοξυριβοζονουκλεϊνικό οξύ, είτε σαν το ελαφρώς πιο σύντομο: δεοξυριβονουκλεϊκό οξύ.

Όπως δείχνει το παραπάνω μοντέλο του DNA στην εικόνα, οι χημικές βάσεις αδενίνη (Α), θυμίνη (Θ), γουανίνη (Γ), και κυτοσίνη (Κ) βρίσκονται στα έγχρωμα ελικοειδή τμήματα που σχηματίζουν τη διπλή έλικα. Τα οριζόντια “σκαλοπάτια” είναι τα σάκχαρα που τις ενώνουν. Η έλικα αυτή συνεχίζεται με χιλιάδες τέτοια “σκαλοπάτια”. Οι Α, Θ, Γ, και Κ είναι που κωδικοποιούν όλα τα γενετικά χαρακτηριστικά όλων των έμβιων όντων. Το αν θα έχουμε μπλε ή καστανά μάτια, ξανθά ή μαύρα μαλλιά, αν θα γίνουμε ψηλοί ή κοντοί, αν ο χαρακτήρας-μας θα είναι πράος ή οξύθυμος, αν θα τείνουμε να γίνουμε θρήσκοι ή άθεοι, και χίλιες-δυο άλλες ιδιότητες της φυσικής και της ψυχολογικής-μας υπόστασης, καθορίζονται εν μέρει από τη σειρά με την οποία εμφανίζονται τα Α, Θ, Γ, και Κ που συνιστούν το DNA του καθενός-μας. (Εν μέρει μόνο, γιατί τα χαρακτηριστικά-μας επίσης επηρεάζονται από το περιβάλλον στο οποίο μεγαλώνουμε· π.χ., καταναλώνοντας τροφές πλούσιες σε κάποια είδη πρωτεϊνών μπορούμε να γίνουμε ελαφρώς πιο ψηλοί απ’ ότι αν δεν καταναλώναμε τέτοιες πρωτεΐνες· μεγαλώνοντας σε μια κοινωνία ισχυρά θρησκευόμενη μπορεί να γίνουμε πιο θρήσκοι απ’ ότι αν μεγαλώναμε σε κοινωνία μη θρήσκων ατόμων· κ.ο.κ.)

Η γνώση της δομής του DNA και του τρόπου με τον οποίο κωδικοποιούνται τα γενετικά χαρακτηριστικά έχει τεράστια σημασία στην κατανόηση του βιολογικού κόσμου, αλλά και επιπτώσεις στην καθημερινή ζωή-μας:

Θεμελίωση της μοντέρνας γλωσσολογίας

Από όλους τους θεμελιωτές ή “πατέρες” μιας επιστήμης που εξετάστηκαν στο παρόν μάθημα, υπάρχει μόνον ένας που είναι ακόμα εν ζωή, τουλάχιστον μέχρι τον καιρό που γράφονται οι παρούσες σημειώσεις. Πρόκειται για το θεμελιωτή της μοντέρνας γλωσσολογίας, Αμερικανό γλωσσολόγο, νοολόγο, φιλόσοφο, και πολιτικό ακτιβιστή Noam Chomsky. (Το όνομά του προφέρεται “Νόουμ” στα αγγλικά, αλλά το “Νόαμ” έχει επικρατήσει στη γλώσσα-μας, οπότε αυτό θα χρησιμοποιήσουμε.)

Noam Chomsky (Νόαμ Τσόμσκι, 1928 –)

Επομένως μια γλώσσα όπως η ελληνική δεν είναι μόνο αυτό που έχει μιληθεί και έχει γραφεί από τους ομιλητές της ελληνικής μέχρι σήμερα, αλλά και αυτό που θα μπορούσε να ομιληθεί, και αυτό που δεν θα ομιληθεί ποτέ — γιατί προτάσεις παρόμοιες με την «Άχρωμες πράσινες ιδέες...» (και μάλιστα με δεκάδες λέξεις αλλά γραμματικά τοποθετημένες) δεν θα παραχθούν ποτέ. Μάλιστα αυτή η “εν δυνάμει ελληνική” (δηλαδή οι προτάσεις που ανήκουν στη γλώσσα αλλά δεν θα παραχθούν ποτέ, είτε γιατί στερούνται νοήματος, είτε γιατί έχουν νόημα αλλά θα χρειάζονταν εκατομμύρια χρόνια για να παραχθούν) έχει γιγαντιαίο μέγεθος συγκρινόμενη με την “ήδη παραχθείσα ελληνική”. (Αν κάνουμε την υπόθεση οτι οι προτάσεις μπορούν να είναι και ατέρμονες, τότε η “εν δυνάμει ελληνική” έχει άπειρο μέγεθος.) Το ίδιο φυσικά ισχύει για κάθε γλώσσα.

Μια από τις ιδέες του Τσόμσκι που επηρέασαν βαθύτατα τη γλωσσολογία ήταν οτι κάθε βρέφος, ερχόμενο στον κόσμο, διαθέτει ήδη (από γεννησιμιού-του) μια “γλωσσολογική μηχανή” (αγγλ.: linguistic module) που περιλαμβάνει μια αφηρημένη, γενικής μορφής γλώσσα. Με τη γενική αυτή γλώσσα, το βρέφος χρειάζεται ν’ ακούσει μόνο λίγα παραδείγματα από τη γλώσσα του περιβάλλοντός του (αυτήν που θα γίνει “μητρική-του” γλώσσα) για να βάλει τις σωστές τιμές στις παραμέτρους της γενικής γλώσσας και να την προσαρμόσει έτσι σ’ αυτήν που ακούει. Παράδειγμα: στην ελληνική βάζουμε συνήθως πρώτα το υποκείμενο [Υ], μετά το ρήμα [Ρ], και μετά το αντικείμενο [Α] (π.χ.: «το ποτάμι [Υ] πλημμύρισε [Ρ] τον κάμπο [Α]»). Επίσης σε γλώσσες όπως η αγγλική η σύνταξη Υ–Ρ–Α είναι υποχρεωτική. Σε γλώσσες όμως όπως τα ιαπωνικά και τα τουρκικά η σειρά είναι: Υ–Α–Ρ, δηλαδή το ρήμα μπαίνει στο τέλος. Η γενική γλώσσα δεν ασχολείται με το με ποια σειρά θα μπουν τα τρία αυτά στοιχεία· απλά γνωρίζει οτι υπάρχουν. Όταν το βρέφος μεγαλώνει στην Ελλάδα ή σε αγγλοσαξωνική χώρα, μαθαίνει οτι η σωστή τιμή της παραμέτρου “σειρά των τριών αυτών στοιχείων” είναι Υ–Ρ–Α· ενώ αντίθετα αν μεγαλώσει στην Ιαπωνία ή Τουρκία θα μάθει οτι η σωστή τιμή είναι η Υ–Α–Ρ. Παρόμοια για δεκάδες ή εκατοντάδες άλλες παραμέτρους που “εξειδικεύουν” τη γενική γλώσσα και την προσαρμόζουν στη μητρική.

Με τον τρόπο αυτόν ο Τσόμσκι εξήγησε το πώς είναι δυνατό τα βρέφη να αποκτούν σε τόσο σύντομο χρονικό διάστημα ένα ποσό γνώσης που μπορεί να πτοήσει οποιονδήποτε ενήλικο· επίσης το πώς μπορούν να παράγουν γραμματικά σωστές ως επί το πλείστον λέξεις και φράσεις, ενώ αν βασίζονταν μόνο σ’ αυτά που ακούνε θα έπρεπε οι παραγωγές-τους να είναι τόσο λανθασμένες όσο και σωστές. Το πρόβλημα αυτό λέγεται “φτώχεια του ερεθίσματος” (αγγλ.: “poverty of the stimulus”), και αναφέρεται στο γεγονός οτι τα γλωσσικά δεδομένα που προσλαμβάνουν τα νήπια από το περιβάλλον-τους είναι πολύ φτωχά για να εξηγήσουν τις εντυπωσιακές γλωσσικές επιδόσεις των νηπίων. Η έμφυτη γενική γραμματική είναι μια λύση στο πρόβλημα αυτό.

Αυτά τα θέματα γλωσσολογίας, όπως και πολλά άλλα, εξετάζονται με περισσότερες λεπτομέρειες στο εισαγωγικό μάθημα Γ1.

Η συνεισφορά του Τσόμσκι στη γλωσσολογία είναι βέβαια πολύ μεγαλύτερη από όσο μπορεί να συνοψιστεί στις παραπάνω γραμμές. Παράλληλα με τη γλωσσολογία, ο Τσόμσκι έχει αναπτύξει και φιλοσοφικές αλλά και πολιτικές θέσεις, που κλίνουν προς την άποψη της αναρχίας. (Με την υποσημείωση οτι με τον όρο “αναρχία” ο Τσόμσκι δεν εννοεί την κατεδάφιση των πάντων, αλλά τη σημαντική ελάττωση των κοινωνικών δομών και του βαθμού στον οποίο ασκείται η εξουσία.) Συγκαταλέγεται ανάμεσα στους δέκα συγγραφείς που αναφέρονται περισσότερο απ’ όλους στις ανθρωπιστικές επιστήμες, μπροστά από τους Χέγκελ και Κικέρωνα, και έπεται μόνο των Μαρξ, Λένιν, Σαίξπηρ, Αριστοτέλη, Πλάτωνα, και Φρόυντ, ενώ σήμερα (2012) είναι ο μόνος ζωντανός από αυτούς (βλ. Στήβεν Πίνκερ, «Το γλωσσικό ένστικτο», σ. 27).

Κατά τις τελευταίες δεκαετίες του 20^ού αιώνα και την αρχή του 21^ου έχουν υπάρξει ενδιαφέροντα επιστημονικά βήματα προόδου, όπως η ανακάλυψη πλανητών σε άλλα ηλιακά συστήματα και η κατανόηση της διαδικασίας δημιουργίας αστέρων και πλανητών στην αστρονομία, η αποκωδικοποίηση του ανθρώπινου γονιδιώματος στη βιολογία (με αναμενόμενα οφέλη στην ιατρική), η καλύτερη κατανόηση της ανθρώπινης νόησης στη νοολογία, η πειραματική επιβεβαίωση της ύπαρξης σωματιδίων που είχαν προταθεί θεωρητικά στην κβαντική φυσική (π.χ. μποζόνιο του Higgs, που μας επιτρέπει να λέμε οτι «κατανοούμε πλέον τί είναι η μάζα»), και άλλα πολλά. Κανένα όμως από αυτά — κατά την κρίση του συγγραφέα του παρόντος — δεν είναι τόσο σημαντικό όσο αυτά που ήδη αναφέρθηκαν ώστε να διεκδικήσει μία ιδιαίτερη παράγραφο στις παρούσες σημειώσεις.

Ιστορία και Εξέλιξη της Επιστήμης

Η επανάσταση της φυσικής του 20ού αιώνα