 |
Ιστορία και Εξέλιξη της ΕπιστήμηςΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ Ε2 ΤΟΥ Δ.Ε.Π. |
Προεπιστήμονες (“φυσικοί φιλόσοφοι”) της αρχαίας Ελλάδας
Στο μάθημα Ε1 είδαμε οτι ο όρος “επιστήμη” έχει πάρει σήμερα διαφορετικό νόημα από αυτό το οποίο είχε στην αρχαιότητα. Όμως η επιστήμη με τη σημερινή-της έννοια δεν ξεπήδησε ξαφνικά κατά την εποχή της Αναγέννησης εκ του μηδενός, αλλά είχε τις ρίζες-της στην αρχαιότητα, και συγκεκριμένα στη σκέψη των “φυσικών φιλοσόφων” της αρχαίας Ελλάδας. Βέβαια ούτε οι αρχαίοι Έλληνες ξεκίνησαν εκ του μηδενός. Θα πρέπει να υπήρξαν διανοητές των μεσανατολικών χωρών που να ξεκίνησαν κάποιες σκέψεις, τους οποίους δεν γνωρίζουμε. Όπως όμως θα δούμε, η φιλοσοφία των Ελλήνων διέφερε από την Ανατολική σε κάποια ουσιαστικά σημεία.
Αυτό το οποίο εισήγαγαν οι αρχαίοι Έλληνες διανοητές, που ήταν η καινοτόμος ιδέα που διαχωρίζει την ελληνική σκέψη από εκείνη όλης της προηγούμενης αρχαιότητας, είναι κυρίως η ιδέα οτι πρέπει να υπάρχει μια φυσική εξήγηση για κάθε φυσικό γεγονός. Δηλαδή ενώ λαοί όπως οι Βαβυλώνιοι, οι Αιγύπτιοι, οι Εβραίοι, κλπ., εξηγούσαν έναν κατακλυσμό (πλημμύρα τοπικού χαρακτήρα) ως το αποτέλεσμα της οργής κάποιου θεού που θύμωσε και έπνιξε όλο τον κόσμο, οι αρχαίοι Έλληνες — ή τουλάχιστον κάποιοι διανοητές μεταξύ αυτών — προσπαθούσαν να βρουν τη φυσική εξήγηση, αποφεύγοντας την επίκληση στο υπερφυσικό, το θείο, το μυστήριο, και κατά συνέπεια το ανεξιχνίαστο. Αυτή είναι λοιπόν η ουσιαστική συμβολή των Ελλήνων: οτι υπέθεσαν πως ο κόσμος είναι κατανοήσιμος από τον ανθρώπινο νου. Αντίθετα, όταν κανείς εισάγει το υπερφυσικό ως εξήγηση, αυτόματα είναι σαν να παραιτείται από την προσπάθεια κατανόησης της φύσης, αφού το “γιατί” είναι θέμα πλέον όχι ανθρώπινο, αλλά υπερφυσικό, άρα άγνωστο στους ανθρώπους (και γνωστό ίσως στους θεούς). Χρειάζεται πραγματικά αρκετή τόλμη για να ξεπεράσει κανείς το φόβο που προκαλεί το άγνωστο, και να σκεφτεί οτι «Ίσως μπορώ να το καταλάβω αυτό το φαινόμενο, και μέσα από την κατανόηση να το δαμάσω, ώστε να μη μου προκαλεί πια φόβο.» Αυτή τη σκέψη μπορεί ενσυνείδητα να μην την έκανε τότε κανείς, αλλά συνάγεται σαν υποσυνείδητη ιδέα μελετώντας τα έργα των αρχαίων Ελλήνων. Έτσι, τους αρχαίους εκείνους διανοητές τους ονομάζουμε “φυσικούς φιλοσόφους”, αφού ήσαν οι πρώτοι που υπέθεσαν τη φυσικότητα της φύσης, και απέρριψαν την υπερφυσικότητά της.
Επίσης τους ονομάζουμε “προεπιστήμονες”, γιατί, ναι μεν δεν γνώριζαν την επιστημονική μέθοδο ώστε να την εφαρμόσουν, αλλά η σκέψη-τους πλησίασε προς κάποια βασικά χαρακτηριστικά της σημερινής επιστήμης. Συγκεκριμένα:
![]() Προσπάθησαν να αναγάγουν την πολυπλοκότητα της φύσης σε κάποιες απλές
και στοιχειώδεις οντότητες. Όπως θα δούμε στη συνέχεια, ο Θαλής είπε οτι
τα πάντα στον κόσμο ανάγονται στο νερό, ο Ηράκλειτος στο πυρ, και ούτω
καθεξής. Αυτή η προσπάθεια αναγωγής του πολύπλοκου κόσμου που μας
περιβάλλει σε λίγα και απλούστερα συστατικά είναι βασικό στοιχείο της
σημερινής επιστημονικής σκέψης (βλ. και “ξυράφι του Όκαμ” στο Ε1).
Προσπάθησαν να αναγάγουν την πολυπλοκότητα της φύσης σε κάποιες απλές
και στοιχειώδεις οντότητες. Όπως θα δούμε στη συνέχεια, ο Θαλής είπε οτι
τα πάντα στον κόσμο ανάγονται στο νερό, ο Ηράκλειτος στο πυρ, και ούτω
καθεξής. Αυτή η προσπάθεια αναγωγής του πολύπλοκου κόσμου που μας
περιβάλλει σε λίγα και απλούστερα συστατικά είναι βασικό στοιχείο της
σημερινής επιστημονικής σκέψης (βλ. και “ξυράφι του Όκαμ” στο Ε1).
![]() Έκαναν
έρευνα και φιλοσοφική σκέψη μόνο και μόνο για χάρη της σκέψης,
χωρίς να περιμένουν κάποιο πρακτικό αποτέλεσμα. Αυτό βρίσκεται σε
κατευθείαν αντίθεση με τη σκέψη άλλων σύγχρονών τους λαών, οι οποίοι
έκαναν τις σκέψεις μόνο όταν έβλεπαν κάποιο πρακτικό αποτέλεσμα. Οι
Αιγύπτιοι, π.χ., προχώρησαν σε μια τελείως πρακτική γνώση της
γεωμετρίας, μέσω της οποίας μπορούσαν να επαναπροσδιορίζουν τα όρια των
αγρών-τους όταν αυτά σκεπάζονταν από λάσπη μετά από τις περιοδικές
πλημμύρες του Νείλου. Οι Βαβυλώνιοι ανέπτυξαν την αστρονομία για να
μπορούν να έχουν ακριβή γνώση του πιο κατάλληλου χρόνου για τη σπορά των
σιτηρών. Αντίθετα, οι Έλληνες διατύπωσαν π.χ. το Πυθαγόρειο θεώρημα, ή
το θεώρημα του Θαλή, χωρίς να έχουν κάποια εφαρμογή κατά νου. Η σημερινή
έρευνα στην επιστήμη έχει επίσης το ίδιο χαρακτηριστικό: συχνά
προηγείται των εφαρμογών, οι οποίες ανακαλύπτονται αργότερα. Όποτε η
έρευνα “σύρεται” από τις εφαρμογές καταντάει να προχωρά στα τυφλά, χωρίς
όραμα και χωρίς ουσιαστικές προοπτικές σε βάθος χρόνου.
Έκαναν
έρευνα και φιλοσοφική σκέψη μόνο και μόνο για χάρη της σκέψης,
χωρίς να περιμένουν κάποιο πρακτικό αποτέλεσμα. Αυτό βρίσκεται σε
κατευθείαν αντίθεση με τη σκέψη άλλων σύγχρονών τους λαών, οι οποίοι
έκαναν τις σκέψεις μόνο όταν έβλεπαν κάποιο πρακτικό αποτέλεσμα. Οι
Αιγύπτιοι, π.χ., προχώρησαν σε μια τελείως πρακτική γνώση της
γεωμετρίας, μέσω της οποίας μπορούσαν να επαναπροσδιορίζουν τα όρια των
αγρών-τους όταν αυτά σκεπάζονταν από λάσπη μετά από τις περιοδικές
πλημμύρες του Νείλου. Οι Βαβυλώνιοι ανέπτυξαν την αστρονομία για να
μπορούν να έχουν ακριβή γνώση του πιο κατάλληλου χρόνου για τη σπορά των
σιτηρών. Αντίθετα, οι Έλληνες διατύπωσαν π.χ. το Πυθαγόρειο θεώρημα, ή
το θεώρημα του Θαλή, χωρίς να έχουν κάποια εφαρμογή κατά νου. Η σημερινή
έρευνα στην επιστήμη έχει επίσης το ίδιο χαρακτηριστικό: συχνά
προηγείται των εφαρμογών, οι οποίες ανακαλύπτονται αργότερα. Όποτε η
έρευνα “σύρεται” από τις εφαρμογές καταντάει να προχωρά στα τυφλά, χωρίς
όραμα και χωρίς ουσιαστικές προοπτικές σε βάθος χρόνου.
![]() Διατύπωσαν για πρώτη φορά την έννοια της απόδειξης, μέσω της
οποίας γινόμαστε 100% βέβαιοι οτι μια μαθηματική πρόταση είναι σωστή.
Δηλαδή: ο Βαβυλώνιος π.χ. παρατηρητής μπορεί να παρατηρούσε οτι όποτε
έφερνε τις διαμέσους ενός τριγώνου (βλ. εικόνα), αυτές φαίνονταν να
τέμνονται (και οι τρεις) σε ένα σημείο. Ήταν αυτό σύμπτωση; Πάντα θα
συμβαίνει, ή μήπως υπάρχει κάποιο τρίγωνο στο οποίο οι διάμεσοι δεν
περνούν και οι τρεις από το ίδιο σημείο;
Διατύπωσαν για πρώτη φορά την έννοια της απόδειξης, μέσω της
οποίας γινόμαστε 100% βέβαιοι οτι μια μαθηματική πρόταση είναι σωστή.
Δηλαδή: ο Βαβυλώνιος π.χ. παρατηρητής μπορεί να παρατηρούσε οτι όποτε
έφερνε τις διαμέσους ενός τριγώνου (βλ. εικόνα), αυτές φαίνονταν να
τέμνονται (και οι τρεις) σε ένα σημείο. Ήταν αυτό σύμπτωση; Πάντα θα
συμβαίνει, ή μήπως υπάρχει κάποιο τρίγωνο στο οποίο οι διάμεσοι δεν
περνούν και οι τρεις από το ίδιο σημείο;
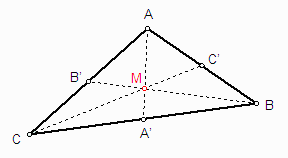
Τρίγωνο ABC και
διάμεσοι AA΄, BB΄,
και CC΄.
Τέμνονται κατά τύχη καί οι τρεις διάμεσοι στο σημείο
Μ, ή πάντα συμβαίνει αυτό;
Αντίθετα, οι Έλληνες κατάφεραν και απέδειξαν οτι αυτό πάντα ισχύει. (Όχι βέβαια μόνο αυτό, αλλά και χιλιάδες άλλα συμπεράσματα της γεωμετρίας.) Από τη στιγμή που βρίσκουμε μια απόδειξη, παύουμε να αμφιβάλλουμε, θεωρούμε το συμπέρασμα σαν δεδομένο, και προχωρούμε σε επόμενα ερωτήματα και συμπεράσματα. Όταν η απόδειξη δεν υπάρχει, διατηρούμε την αμφιβολία, επομένως οτιδήποτε και να συνάγουμε στο μέλλον που να στηρίζεται στο παρόν, θα είναι εξίσου αμφίβολο όσο και το παρόν συμπέρασμα. Αν το παρόν συμπέρασμα καταρριφθεί στο μέλλον, τότε καταρρίπτεται και όλο το οικοδόμημα το οποίο στηρίξαμε πάνω-του. Επομένως χωρίς αποδείξεις, το οποιοδήποτε μαθηματικό οικοδόμημα “τελεί υπό κατάρρευση” ανά πάσα στιγμή. Αυτό το πρόβλημα αποφεύγει η αποδεικτική μέθοδος των Ελλήνων, που εισάγει έτσι τη μαθηματική βεβαιότητα.
Ας εξετάσουμε τώρα έναν-έναν τους κυριότερους φυσικούς φιλοσόφους της αρχαίας Ελλάδας. Θα σταθούμε στις φιλοσοφικές-τους απόψεις περί φύσης, και όχι στις ηθικές ή άλλες απόψεις που τυχόν διατύπωσαν.
Προχωράμε χρονολογικά, ξεκινώντας με τους τρεις “Μιλήσιους”: Θαλής, Αναξίμανδρος, Αναξιμένης, που ο πρώτος υπήρξε δάσκαλος του δεύτερου, και ο δεύτερος του τρίτου.
Θαλής (~624 – ~546 π.Χ.)
Σύμφωνα με τον φιλόσοφο του 20ού αιώνα Bertrand Russell (Μπέρτραντ Ράσσελ), «Η Δυτική φιλοσοφία αρχίζει με τον Θαλή». Την ίδια γνώμη είχε και ο Αριστοτέλης (στα Μεταφυσικά, Α΄).
 |
Ο Θαλής υπέθεσε οτι η πρωταρχική φύση του κόσμου είναι το νερό, και οτι από αυτό προέρχονται όλα τα υπόλοιπα. Ο Ηράκλειτος ο Ομηρικός(*) αναφέρει οτι ο Θαλής έφτασε σ’ αυτό το συμπέρασμα βλέποντας πως τα υγρά μεταβάλλονται σε αέρα, και οτι η υγρή γη μεταβάλλεται σε στερεή (όταν ξεραίνεται). Άρα, κατά τον Θαλή, τόσο τα αέρια οσο και τα στερεά προέρχονται από το νερό. Μάλιστα, ολόκληρη η Γη δεν είναι παρά το στερεοποιημένο νερό του Ωκεανού που την περιβάλλει. Και ποια ήταν η γνώμη-του για τις θεότητες; Μήπως και ο θεός προέρχεται από το νερό; Όχι βέβαια. Ο Θαλής παραδεχόταν το νερό σαν πρωταρχικό στοιχείο των φυσικών πραγμάτων. Για τα θεϊκά, πίστευε οτι ανήκαν σε διαφορετική, μη φυσική σφαίρα. Ο Κικέρων αναφέρει οτι ο Θαλής πίστευε πως ο θεός είναι εκείνος ο Νους που δημιούργησε και έδωσε μορφή σε όλα τα φυσικά αντικείμενα, χρησιμοποιώντας το νερό σαν πρώτη ύλη. |
Ο Θαλής προσπάθησε να δώσει φυσική εξήγηση στους σεισμούς, λέγοντας οτι καθώς η Γη επιπλέει πάνω στον Ωκεανό, οι σεισμοί συμβαίνουν όταν τα κύματα του Ωκεανού χτυπούν και σείουν τη Γη. Μπορεί να είναι λάθος σαν ιδέα, αλλά έχει το πλεονέκτημα της απαγγίστρωσης από την υπερφυσική εξήγηση (π.χ., ο γίγας Εγκέλαδος που σείει τη Γη από τα έγκατα του ηφαιστείου της Αίτνας).
Έκανε και ουσιαστικές συνεισφορές στη γεωμετρία. Προφανώς γνώριζε περί όμοιων τριγώνων, γιατί ο Διογένης ο Λαέρτιος αναφέρει οτι ο Θαλής μέτρησε το ύψος μιας Αιγυπτιακής πυραμίδας από το μήκος της σκιάς-της, κατά την ώρα που το μήκος της δικής-του σκιάς ήταν ίσο με το ύψος-του. (Βέβαια γνωρίζοντας περί ομοίων τριγώνων μπορούμε να κάνουμε τον υπολογισμό χωρίς να περιμένουμε να γίνουν ίσα τα δύο μήκη· ίσως η ιστορία να οφείλεται σε ελλιπή γεωμετρική γνώση από το Διογένη το Λαέρτιο.)
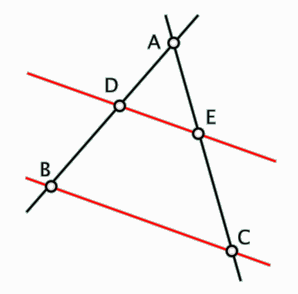
Το “θεώρημα του Θαλή”: AD/AB = AE/AC = DE/BC.
Δύο θεωρήματα της γεωμετρίας αποδίδονται στο Θαλή, με πιο γνωστό εκείνο που φαίνεται στο παραπάνω σχήμα. Υπάρχει και ένα δεύτερο, που αφορά σε τρίγωνο εγγεγραμένο σε κύκλο, όπου μια πλευρά του τριγώνου είναι διάμετρος του κύκλου. Και άλλα θέματα της γεωμετρίας αποδίδονται στον Θαλή, μάλλον όμως λόγω “υπερβάλλοντος ζήλου” για να του αποδοθούν πολλά, καθώς θεωρείτο ένας από τους “επτά σοφούς” της αρχαιότητας.
Αναξίμανδρος (~610 – ~546 π.Χ.)
Ο μαθητής του Θαλή (αλλά μόλις περίπου κατά 14 χρόνια νεώτερός του) Αναξίμανδρος θεώρησε οτι η αρχή του κόσμου είναι το “άπειρο”, και σύμφωνα με τον Αριστοτέλη, ήταν αυτός που εισήγαγε τον όρο “άπειρον”.
 |
Το άπειρο αυτό, σύμφωνα με τον Αναξίμανδρο, ούτε μεγαλώνει σε ηλικία, ούτε αποσυντίθεται, αλλά είναι αιώνιο, δηλαδή δεν έχει αρχή ούτε τέλος. Παράγει όμως συνεχώς καινούρια ύλη από την οποία συντίθενται όλα όσα παρατηρούμε. Ο Αναξίμανδρος διαφώνησε φιλοσοφικά με τον μέντορά του Θαλή, ισχυριζόμενος οτι το νερό δεν μπορεί να είναι η αρχή των πάντων, αφού το νερό είναι πάντα υγρό, ποτέ ξερό όπως η γη, και ποτέ καυτό όπως η φωτιά. Είπε οτι κανένα από τα γνωστά υλικά (αέρας, φωτιά, κλπ.) δεν μπορεί να είναι από μόνο-του υπεύθυνο για όλα όσα παρατηρούμε γύρω-μας, γιαυτό ανέθεσε αυτόν το ρόλο σε μια αφηρημένη έννοια όπως το άπειρο. Οι υλικές οντότητες όταν πεθαίνουν και αποσυντίθενται επιστρέφουν στην αρχική κατάσταση, δηλαδή στο άπειρο. Σύμφωνα με το κοσμολογικό σχέδιο του Αναξίμανδρου, η Γη έχει το σχήμα πεπλατυσμένου κυλίνδρου, με ύψος ίσο με το 1/3 του πλάτους (διαμέτρου)-του. Οι άνθρωποι και η υπόλοιπη ζωντανή φύση κατοικούν στην επάνω επίπεδη επιφάνεια του κυλίδρου, ενώ όλος ο κύλινδρος είναι ακίνητος στο μέσον του απείρου, χωρίς να στηρίζεται πουθενά. Γιατί δεν κινείται; Διότι δεν έχει κανένα λόγο να κινηθεί προς κάπου. |
Εξήγησε τα ουράνια σώματα (Ήλιος, Σελήνη, αστέρες) ως εξής: είπε οτι σε μεγάλη απόσταση από τη Γη υπάρχουν τροχοί ομόκεντροι με τη Γη. Πίσω από αυτούς τους τροχούς υπάρχει το πρωταρχικό πυρ του απείρου από το οποίο δημιουργήθηκε και η Γη. Τα ουράνια σώματα είναι απλώς τρύπες στους τροχούς αυτούς, και μέσα από τις τρύπες αυτές βλέπουμε το αρχέγονο πυρ. Ο Ήλιος, π.χ. είναι μια μεγάλη τρύπα, ίσου μεγέθους με τη Γη, στον πιο απομακρυσμένο τροχό. Ολόκληρος ο τροχός αυτός με την τρύπα του Ήλιου έχει διάμετρο 27 ή 28 φορές τη διάμετρο του κυλίνδρου της Γης. Οι ηλιακές εκλείψεις συμβαίνουν όταν η τρύπα αυτή καλύπτεται. Ο τροχός της οπής της Σελήνης έχει 18 ή 19 φορές τη διάμετρο της Γης, και το φώς πίσω από αυτόν τον τροχό είναι πιο αδύναμο (γιαυτό η Σελήνη δεν είναι τόσο φωτεινή όσο ο Ήλιος). Τέλος, ο τροχός των άστρων είναι ακόμα πιο κοντά στη Γη, με διάμετρο 9 ή 10 φορές τη διάμετρο της Γης. (Είναι άγνωστο το πώς εξήγησε ο Αναξίμανδρος το οτι δεν βλέπουμε ποτέ τα άστρα νε έρχονται εμπρός από το Φεγγάρι.) Φυσικά και τα άστρα είναι οπές στο δικό-τους τροχό.
Άλλες ενδιαφέρουσε απόψεις του Αναξίμανδρου είναι οτι υπάρχουν πολλοί κόσμοι, όχι μόνο αυτός που παρατηρούμε. Κάθε κόσμος δημιουργείται, εξακολουθεί να υπάρχει για κάποιο διάστημα, και κάποτε χάνεται, αλλά αυτό συμβαίνει ταυτόχρονα και με πολλούς άλλους κόσμους.
Σχεδίασε επίσης έναν παγκόσμιο χάρτη, που θα πρέπει να έμοιαζε ως εξής:
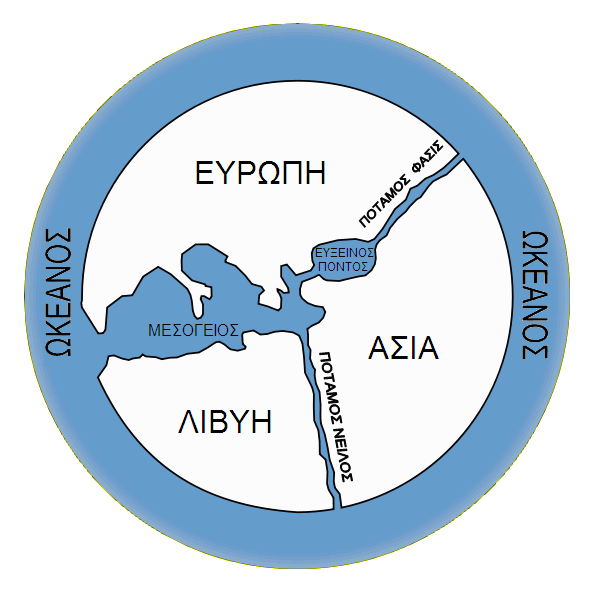
Αυτός ήταν ίσως ένας από τους πρώτους χάρτες ολόκληρου του τότε γνωστού κόσμου. Ας σημειωθεί οτι ο “τεράστιος” ποταμός Φάσις (που αναφέρεται στον Ησίοδο και στον Ηρόδοτο, και που οι αρχαίοι Έλληνες θεωρούσαν σαν το όριο μεταξύ Ευρώπης και Ασίας), είναι στην πραγματικότητα ένας πολύ μικρός ποταμός που σήμερα λέγεται Ριόνι, βρίσκεται εξ ολοκλήρου μέσα στο έδαφος της Γεωργίας, και πηγάζει από τις οροσειρές του Καυκάσου.
Ο Αναξίμανδρος θεωρείται ο πρώτος φιλόσοφος που διατύπωσε μια εξελικτική θεωρία περί προέλευσης του ανθρώπου. Βέβαια η θεωρία-του δεν έχει κανένα χαρακτηριστικό που να μοιάζει με τη φυσική επιλογή, όπως τη γνωρίζουμε σήμερα. Υποστήριξε οτι η ζωή προήλθε από τη θάλασσα (εν μέρει σωστό!) και οτι οι άνθρωποι ήσαν έγκλειστοι στο εσωτερικό μεγάλων ψαριών, όσο οι συνθήκες στη στεριά ήσαν ακατάλληλες για τη διαβίωση των ανθρώπων. Όταν οι συνθήκες έγιναν όπως τις γνωρίζουμε σήμερα, οι άνθρωποι έφυγαν από το εσωτερικό των ψαριών και κατοίκησαν στη στεριά.
Αναξιμένης (~585 – 528 π.Χ.)
Ο τρίτος στη σειρά φυσικός φιλόσοφος που έδρασε στη Μίλητο ήταν ο Αναξιμένης, μαθητής του Αναξίμανδρου. Αντίθετα με τον μέντορά του, ο Αναξιμένης υποστήριξε οτι όντως υπάρχει μια πρωταρχική φύση όλων των πραγμάτων, και αυτή είναι ο αέρας.
 |
Ο Αναξιμένης στήριξε την πεποίθησή του αυτή σε παρατηρήσεις επί φυσικών διεργασιών. Συγκεκριμένα παρατήρησε οτι όταν ο αέρας ψύχεται υγροποιείται και πέφτει στη γη με τη μορφή βροχής — τουλάχιστον έτσι του φαινόταν οτι συμβαίνει. Άρα, συμπέρανε, το νερό προέρχεται από τον αέρα. Και καθώς ο “υγροποιημένος αέρας” (το νερό δηλαδή) ψύχεται ακόμα περισσότερο, γίνεται πάγος. Επομένως ο αέρας μπορεί να πάρει και στερεή μορφή, άρα από αυτόν προέρχονται και οι πέτρες. Όταν ο αέρας ξηρανθεί και αραιωθεί ακόμα πιο πολύ από τη φυσική-του κατάσταση, τότε καίγεται και εμφανίζεται σαν φωτιά. Άρα όλες οι καταστάσεις της ύλης που ήσαν γνωστές στην αρχαιότητα (φωτιά, νερό, γη, και αέρας), προέρχονται τελικά από μία: τον αέρα. Η Γη, είπε, είναι σαν φύλο που μένει μετέωρο μέσα σε ένα ρεύμα αέρα. Τα αστέρια δημιουργήθηκαν όταν η Γη παρήγαγε μια ανάσα αέρα που πήρε φωτιά σε αμέτρητα σημεία στον ουράνιο θόλο. |
Ο Ήλιος όμως δεν αποτελείται από αραιωμένο αέρα όπως τα άστρα, αλλά από γη, όπως και το Φεγγάρι. Ο λόγος που ο Ήλιος είναι τόσο ζεστός είναι οτι κινείται πολύ γρήγορα, οπότε η ταχύτητά του (μέσω της τριβής με τον αέρα) τον κάνει να καίει. Όταν δύει, ο Ήλιος δεν πάει κάτω από τη Γη, απλώς γυρνάει γύρω-γύρω, κρυμένος από τα μακρυνά βουνά, ώσπου να φτάσει στην ανατολή. Τόσο τον Ήλιο όσο και τη Σελήνη τα θεωρούσε επίπεδους δίσκους.
Για τους σεισμούς, ο Αναξιμένης έδωσε την εξήγηση οτι οφείλονται σε ρωγμές στα έγκατα της Γης, που δημιουργούνται είτε λόγω ξηρασίας, είτε — το αντίθετο — λόγω υπερβολικής ποσότητας νερού. Όταν οι ρωγμές γίνονται μεγάλες, ολόκληροι λόφοι πέφτουν μέσα σ’ αυτές και παράγουν τους σεισμούς. Αυτή η εξήγηση, παρόλο που δεν σχετίζεται με τη σύγχρονη θεωρία των τεκτονικών πλακών, εντούτοις όσο αφορά στις ρωγμές και στις κατακρημνίσεις μαζών εδάφους φαίνεται να πετυχαίνει διάνα.
Επίσης ο Αναξιμένης εξήγησε το ουράνιο τόξο σαν το αποτέλεσμα του περάσματος των ακτίνων του Ήλιου μέσα από στρώματα υγροποιημένου αέρα. Αν αντικαταστήσουμε τον “υγροποιημένο αέρα” με τους “υδρατμούς”, έχουμε και πάλι μια ολόσωστη εξήγηση, ή τουλάχιστον σε πολύ πιο σωστή επιστημονική βάση από τη γνωστή αρχαία Εβραϊκή που αναφέρεται στην Παλαιά Διαθήκη.
Πυθαγόρας (~570 – ~495 π.Χ.)
Ο Πυθαγόρας είναι μια από τις πιο αινιγματικές φυσιογνωμίες των διανοητών της αρχαιότητας. Οι πρώτες σωζόμενες αναφορές σ’ αυτόν μας έρχονται από αιώνες αργότερα.
 |
Υποθέτοντας οτι υπήρξε ο άνθρωπος αυτός, μεταξύ αυτών που γνωρίζουμε είναι οτι, σύμφωνα με τον Ηρόδοτο, πατέρας-του ήταν ο Μνήσαρχος, και γεννήθηκε στη Σάμο, αλλά κατά το 530 π.Χ. μετοίκησε στον Κρότωνα, την ελληνική αποικία της νότιας Ιταλίας, όπου ίδρυσε μια θρησκευτική ομάδα πιστών και μαθητών-του. Σύμφωνα με τον Ηράκλειτο, ο Πυθαγόρας ήταν άνθρωπος πολλών γνώσεων αλλά χωρίς βαθειά κατανόηση, ενώ σύμφωνα με τον Ξενοφάνη, πίστευε στη μετεμψύχωση των ψυχών. Αυτό το οποίο είναι ίσως το πιο αξιοσημείωτο από την άποψη της παρούσας ανασκόπησης είναι αυτό που ο Πυθαγόρας (ή ίσως η Πυθαγόρειος Σχολή) υπέθεσε οτι είναι η αρχή του παντός: οι αριθμοί. Μπορεί ο Θαλής να υπέθεσε σαν αρχή των πάντων το νερό, ο Αναξιμένης τον αέρα, και — όπως θα δούμε στη συνέχεια — ο Ηράκλειτος το πυρ, ο Δημόκριτος τα άτομα, κλπ., αλλά σύμφωνα με την πιο μοντέρνα άποψη της φυσικής (απ’ όσο μπορούμε να γνωρίζουμε σήμερα), πιο κοντά στην αλήθεια απ’ όλους τους αρχαίους φιλοσόφους έφτασε ο Πυθαγόρας, ή οι Πυθαγόρειοι. Πράγματι, οι σημερινοί θεωρητικοί φυσικοί ισχυρίζονται οτι όταν αναλύουμε την ύλη μέχρι τέλους, το μόνο το οποίο μένει είναι οι αριθμοί (σαν φυσικές σταθερές ή αρχικές συνθήκες) και οι μαθηματικές εξισώσεις. |
Πάντως στον περισσότερο κόσμο ο Πυθαγόρας είναι πιο γνωστός για το Πυθαγόρειο θεώρημα, σύμφωνα με το οποίο το τετράγωνο της υποτείνουσας ενός ορθογωνίου τριγώνου είναι ίσο με το άθροισμα των τετραγώνων των δύο άλλων καθέτων πλευρών (βλ. διάγραμμα).
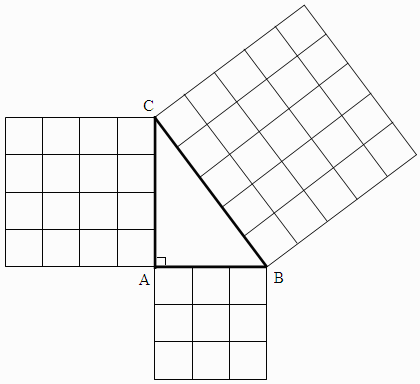
Το Πυθαγόρειο θεώρημα: στο ορθογώνιο
τρίγωνο ABC ισχύει ότι BC2 = AB2
+ AC2.
Αυτό φαίνεται σχηματικά στο διάγραμμα, καθώς το
BC2 = 25, το AB2
= 9, και το AC2 = 16,
οπότε όντως 25 = 9 + 16.
Η σημασία του Πυθαγορείου θεωρήματος (Π.Θ.) δεν είναι οτι μας δίνει απλώς μια μέθοδο υπολογισμού του μήκους της μιας πλευράς ενός ορθογωνίου τριγώνου όταν γνωρίζουμε τα μήκη των άλλων δύο πλευρών. Αν ήταν μόνο αυτό, το Π.Θ. θα ήταν ένα μάλλον ασήμαντο αποτέλεσμα στη γεωμετρία. Η σημασία-του είναι οτι χαρακτηρίζει τον τρόπο με τον οποίο συμπεριφέρονται τα μήκη στην Ευκλείδεια γεωμετρία. Όπως μαθαίνουμε στο μάθημα Μ3 (Γεωμετρίες: Ευκλείδεια – μη Ευκλείδειες), στην Ευκλείδεια γεωμετρία μία ράβδος με μήκος 5 μας φαίνεται να διατηρεί το ίδιο μήκος (οπτικά) όπως και να τη στρέψουμε στο χώρο. Σε μη Ευκλείδειες γεωμετρίες όμως, η ράβδος με μήκος 5 μπορεί να μας φανεί πιο κοντή ή πιο μακριά, ανάλογα με τη γωνία κατά την οποία είναι στραμμένη. Ή για να το πούμε διαφορετικά, η απόσταση μεταξύ δύο σημείων σε μη Ευκλείδειες γεωμετρίες δεν υπολογίζεται μέσω του Π.Θ., αλλά μέσω μιας γενίκευσής του. Αυτό είναι πολύ σημαντικό στη θεωρία της σχετικότητας, γιατί ενώ ο κόσμος μας φαίνεται να ακολουθεί την Ευκλείδεια γεωμετρία, στην πραγματικότητα δεν ισχύει η Ευκλείδεια γεωμετρία, αλλά άλλη, σχετικιστική γεωμετρία (η λεγόμενη υπερβολική γεωμετρία, ή γεωμετρία του Minkowski). Η Ευκλείδεια γεωμετρία είναι μόνο κατά προσέγγιση σωστή (επομένως το ίδιο ισχύει και για το Π.Θ.), όταν οι ταχύτητες είναι πολύ μικρές σε σχέση με την ταχύτητα του φωτός. Αυτά γίνονται καλύτερα κατανοητά στο μάθημα Μ3.
Οι Πυθαγόρειοι είναι επίσης γνωστοί για το οτι αρχικά πίστευαν οτι κάθε αριθμός μπορεί να εκφραστεί σαν κλάσμα δύο ακεραίων. Π.χ., αριθμοί είναι ο 2/3, ο 7/8, ο 87368763/10976088655, κλπ. Κάποτε όμως, ένας από τα μέλη της ομάδας των Πυθαγορείων απέδειξε οτι το μήκος της διαγωνίου ενός τετραγώνου που έχει πλευρά ίση με 1 δεν μπορεί να γραφεί σαν κλάσμα δύο ακεραίων. Τον αριθμό αυτόν σήμερα τον λέμε “τετραγωνική ρίζα του 2” (βλέπε διάγραμμα), αποτέλεσμα που συνάγεται κατευθείαν από το Π.Θ.
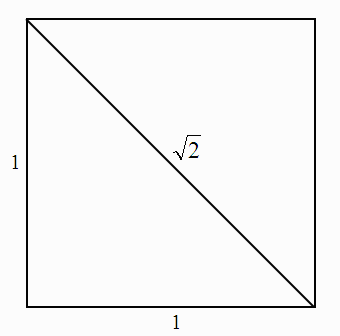
Η διαγώνιος τετραγώνου με πλευρά 1 είναι ίση με την τετραγωνική ρίζα του 2
Εκείνη την εποχή όμως θεώρησαν αυτό το αποτέλεσμα καταστροφικό για την Πυθαγόρεια θεωρία, που έλεγε οτι τα πάντα στο σύμπαν εκφράζονται σαν αναλογίες, δηλαδή είναι κλάσματα ακεραίων. Έτσι αποφάσισαν οτι αυτό έπρεπε να το κρατήσουν μυστικό, και οτι «δεν επιτρέπεται να μιλήσουμε για τους αριθμούς αυτούς», οι οποίοι γιαυτό το λόγο ονομάστηκαν “άρρητοι”, δηλαδή “αυτοί που δεν λέγονται”. Κατ’ αναλογία, οι υπόλοιποι αριθμοί (δηλαδή τα κλάσματα ακεραίων) ονομάστηκαν “ρητοί” (αυτοί που λέγονται). Αργότερα έγινε κατανοητό οτι αριθμοί είναι τόσο οι ρητοί όσο και οι άρρητοι, και όλους μαζί τους λέμε “πραγματικούς αριθμούς”. Βέβαια η θεωρία των Πυθαγορείων οτι τα πάντα στον κόσμο μπορούν να εκφραστούν σαν κλάσματα ακεραίων καταρρίφθηκε από τα δεδομένα, δηλαδή από την παρατήρηση του φυσικού κόσμου). Σύμφωνα με ένα μύθο, τον άνθρωπο που ανακάλυψε τη μη-ρητότητα της τετραγωνικής ρίζας του 2 τον έπνιξαν στη θάλασσα. Αυτό όμως δεν έχουμε ιδέα αν είναι αλήθεια, γιατί αναφέρθηκε σε εποχή πολύ μεταγενέστερη από αυτήν που έδρασαν οι Πυθαγόρειοι.
Ηράκλειτος (~535 – ~475 π.Χ.)
 |
Ο Ηράκλειτος γεννήθηκε στην Έφεσσο της Μικράς Ασίας. Ελάχιστα μόνο αποσπάσματα διασώθηκαν ως τις μέρες-μας σε έργα άλλων φιλοσόφων. Από αυτά που σώθηκαν, μπορούμε να σημειώσουμε δύο σημαντικές ιδέες του Ηράκλειτου για τη φύση του κόσμου: Πρώτο, ο Ηράκλειτος υποστήριξε οτι η αλλαγή (ή αλλιώς θα λέγαμε: η κίνηση) είναι ιδιότητα σύμφυτη με το κάθε τί στον κόσμο. Τα πάντα αλλάζουν, τίποτε δεν μένει το ίδιο. (Αυτή η ρήση περιλαμβάνεται στον Πλάτωνα ως εξής: «πάντα χωρεῖ καὶ οὐδὲν μένει».) Η άποψή του αυτή είναι εκ διαμέτρου αντίθετη με τη μετέπειτα άποψη της Χριστιανικής θεολογίας, που θεωρούσε τον κόσμο στατικό και αναλλοίωτο από τότε που τον δημιούργησε ο Θεός μέχρι σήμερα (πράγμα που εν μέρει ήταν αιτία και της απόρριψης της Δαρβινικής θεωρίας της εξέλιξης). |
Δεύτερο, ο Ηράκλειτος θεώρησε οτι το πρωταρχικό συστατικό του κόσμου είναι το πυρ, πράγμα που συνάγεται από την εξής φράση-του: «Αυτόν τον κόσμο, που είναι ο ίδιος για όλους, κανένας από τους θεούς ή ανθρώπους δεν τον έφτιαξε. Αλλά πάντοτε ήταν και θα είναι: ένα αιώνιο πυρ, με μέρη-του που φλέγονται, και μέρη-του που σβήνουν.» Και επίσης: «Όλα τα πράγματα είναι σε αντάλλαγμα πυρός, και πυρ για όλα τα πράγματα· όπως ανταλλάσονται τα εμπορεύματα για χρυσό, και ο χρυσός για εμπορεύματα.»
Αν θέλαμε να δώσουμε μια κάπως ελεύθερη ερμηνεία των λόγων του Ηράκλειτου, θα μπορούσαμε να πούμε οτι πλησίασε τη μοντέρνα άποψη περί ισοδυναμίας ενέργειας («πυρ») και μάζας («πράγματα») — χωρίς βέβαια αυτό να σημαίνει οτι προανήγγειλε τη γενική θεωρία της σχετικότητας! Απλώς η άποψή του οτι «τα πράγματα είναι σε αντάλλαγμα πυρός» συμβαδίζει με τη σημερινή γνώση της φυσικής που θεωρεί τη μάζα (ύλη) σαν μια μορφή “συμπεπυκνωμένης ενέργειας” (που δίνεται από τον τύπο m = E / c2, όπου m είναι η μάζα, E η ενέργεια, και c2 το τετράγωνο της ταχύτητας του φωτός). Σήμερα θα μπορούσαμε να πούμε: «Η μάζα είναι σε αντάλλαγμα ενέργειας.» Κάποιες ιδέες των αρχαίων Ελλήνων φυσικών φιλοσόφων υπήρξαν πραγματικά εντυπωσιακές.
Εμπεδοκλής (~490 – ~430 π.Χ.)
 |
Γεννήθηκε στον Ακράγαντα της Σικελίας, και θεωρείτο άνθρωπος σοφός και μεγάλων ικανοτήτων από τους συγχρόνους-του. Πρόκειται για το θεμελιωτή της “θεωρίας των τεσσάρων στοιχείων”, που μέσω του Αριστοτέλη επρόκειτο να γίνει η πιο ευρέως αποδεκτή θεωρία για τη σύσταση της ύλης, μέχρι και την Αναγέννηση. Η θεωρία των τεσσάρων στοιχείων (ορολογία που οφείλεται στον Πλάτωνα, καθώς ο Εμπεδοκλής δεν χρησιμοποίησε ποτέ τον όρο “στοιχείο”, αλλά μιλούσε για “ρίζες”), λέει οτι οποιοδήποτε υλικό προέρχεται από μίξη κατάλληλων ποσοτήτων από φωτιά, αέρα, νερό, και γη. Τίποτα το νέο δεν παράγεται πραγματικά στον κόσμο. Οτιδήποτε μας φαίνεται σαν νέο είναι στην πραγματικότητα αποτέλεσμα μιας ανακατανομής των ποσοστών των τεσσάρων στοιχείων. |
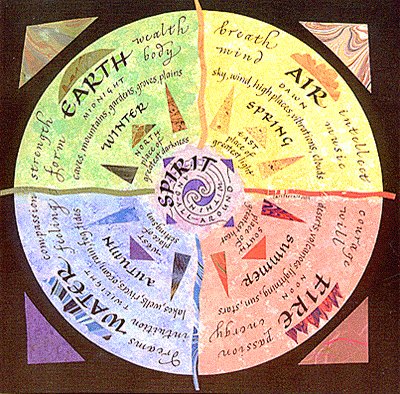
Σημερινός “αστρολογικός χάρτης” βασιζόμενος στη θεωρία των τεσσάρων στοιχείων
Αυτή η άποψη, όπως θα δούμε, είχε συνέπειες πολλούς αιώνες αργότερα, όταν οι αλχημιστές του Μεσαίωνα προσπαθούσαν να φτιάξουν χρυσό. Εφόσον τίποτα δεν δημιουργείται εκ του μηδενός, και κάθε αλλαγή είναι απλώς μια ανακατανομή των τεσσάρων στοιχείων, έπεται οτι και ο χρυσός θα μπορούσε να παραχθεί ανακατεύοντας διάφορα υλικά και αλλάζοντας τις αναλογίες πυρός, αέρα, νερού, και στερεών υλικών. Περισσότερα γι’ αυτό το θέμα όμως θα μάθουμε αργότερα.

Λειτουργία της όρασης κατά τον Εμπεδοκλή: τα μάτια στέλνουν ακτίνες φωτός
Ο Εμπεδοκλής διατύπωσε και μια θεωρία για τις αισθήσεις, και ειδικά για την όραση, που επίσης ήταν λάθος, αλλά επικράτησε λόγω ίσως και πάλι του Αριστοτέλη. Συγκεκριμένα, ο Εμπεδοκλής ισχυρίστηκε οτι τα μάτια-μας στέλνουν φως προς τα αντικείμενα το οποίο τα ακουμπά, οπότε τα βλέπουμε. Δηλαδή “έβαλε το κάρο μπροστά απ’ το άλογο” στη συγκεκριμένη περίπτωση. Σίγουρα δεν θα επέμενε οτι και τον Ήλιο τον βλέπουμε με τον ίδιο τρόπο, αφού είναι περισσότερο από προφανές οτι ο Ήλιος είναι πηγή φωτός, και όχι δέκτης. Είναι όμως ενδιαφέρον οτι για όλα τα υπόλοιπα αντικείμενα πολλοί από τους αρχαίους Έλληνες δεν μπορούσαν να κατανοήσουν οτι τα βλέπουμε γιατί το ηλιακό φως διαχέεται επάνω-τους. (Αναρωτιέται κανείς πώς θα εξηγούσε ο Εμπεδοκλής το γεγονός οτι δεν βλέπουμε τη νύχτα: γιατί παύουν να γίνονται πομποί φωτός τότε τα μάτια-μας;) Η θεωρία οτι τα μάτια-μας είναι πομποί φωτός έχει αφήσει ίχνη στη γλώσσα-μας, όπου λέμε «Ρίξε μια ματιά», και «Άφησε το βλέμμα-της να περιπλανηθεί...».
Δημόκριτος (~460 – ~370 π.Χ.)
 |
Γεννήθηκε στα Άβδηρα της Θράκης. Μαθητής του Λεύκιππου (ενός ακόμα Μιλήσιου), διατύπωσε (ίσως μαζί με τον Λεύκιππο) την ατομική θεωρία, η οποία ουσιαστικά “έμεινε στα αζήτητα” για πάνω από 2.000 χρόνια, μέχρι που άρχισε να γίνεται κατανοητό οτι η θεωρία αυτή βρισκόταν πολύ πιο κοντά στην αλήθεια από τη μέχρι τότε επικρατούσα θεωρία των τεσσάρων στοιχείων του Εμπεδοκλή. Η ατομική θεωρία είχε ομοιότητες, αλλά και διαφορές με τη σημερινή. Τα άτομα των Δημόκριτου και Λεύκιππου ήσαν αδιαίρετα μεν (ά-τομα) αλλά διέφεραν σε γεωμετρικά σχήματα. Ήσαν άπειρα σε αριθμό, αιώνια, άφθαρτα, στερεά, σε αέναη κίνηση, και με κενό χώρο μεταξύ-τους. Εκτός από σχήμα, διέφεραν και σε είδος, και μέγεθος· πιθανώς επίσης και σε βάρος, σύμφωνα με τα γραπτά του Δημόκριτου. Τα άτομα ήσαν στερεά και εφοδιασμένα με μικρούς γάντζους, ώστε να μπορούν να ενώνονται μεταξύ-τους. |
Η ιδέα των “μικρών γάντζων” μπορεί να μας φανεί από πρώτη άποψη αφελής, αλλά αν το καλοσκεφτούμε, τα πραγματικά άτομα όντως έχουν “μικρούς γάντζους”: πρόκειται για τα ηλεκτρόνια της εξωτερικής-τους στοιβάδας, που σχηματίζουν ομοιοπολικούς και ετεροπολικούς δεσμούς, και μ’ αυτόν τον τρόπο επιτρέπουν στα άτομα να ενώνονται σε χημικές ενώσεις. Πάντως η παραδοχή περί “μικρών γάντζων” δείχνει οτι τα άτομα των αρχαίων ατομιστών μπορεί να ήσαν αδιαίρετα, δεν ήσαν όμως στοιχειώδη σε δομή, αφού είχαν διάφορα γεωμετρικά σχήματα και αυτούς τους περίεργους μικρούς γάντζους.
Όλες οι αλλαγές που συμβαίνουν στο μακρόκοσμο δεν είναι παρά αλλαγές στη διαρρύθμιση των ατόμων που αποτελούν τα μακροσκοπικά αντικείμενα, κατά την ατομική θεωρία — άποψη που δεν απέχει και πάρα πολύ από την πραγματικότητα.
Ο Αριστοτέλης διατύπωσε αυστηρή κριτική ενάντια στην ατομική θεωρία, λέγοντας οτι δεν εξηγούσε τί προκάλεσε την πρωταρχική κίνηση των ατόμων. Κατά βάθος ο Αριστοτέλης ήταν οπαδός της τελεολογίας, δηλαδή της άποψης οτι όλα στον κόσμο γίνονται για κάποιο σκοπό. Ο Δημόκριτος πίστευε οτι δεν υπάρχει σκοπός στον κόσμο. Και πώς εξηγούσε το οτι τα πράγματα φαίνονται σαν να γίνονται για κάποιο σκοπό; Πιο συγκεκριμένα, γιατί ο κόσμος δεν είναι ένας ατελείωτος σωρός από άτομα, χωρίς καμιά διαρρύθμιση, αλλά αποτελείται από διακριτά αντικείμενα; Αυτό ο Δημόκριτος το εξηγούσε λέγοντας οτι τα άτομα έχουν την τάση να μαζεύονται “τα όμοια με τα όμοια”. Και από πού προέρχεται αυτή η τάση; Από πουθενά, απαντούσε, και έδινε σαν παράδειγμα τον τρόπο με τον οποίο μαζεύονται τα βότσαλα παρόμοιου μεγέθους μετά από την παλίρροια σε μια παραλία: κανένας δεν “ταξινομεί” τα βότσαλα κατά μέγεθος· απλά υπάρχουν φυσικές δυνάμεις που τα κάνουν να συσσωρεύονται “όμοια με όμοια”. Αφού συσσωρευτούν όμοια άτομα, δημιουργώντας τα μακροσκοπικά αντικείμενα, μας δίνεται η εντύπωση οτι τάχα υπάρχει σκοπός, καθώς και τα μακροσκοπικά αντικείμενα συσσωρεύονται “τα όμοια με τα όμοια” (π.χ., άνθρωποι μεταξύ-τους, ζώα ενός είδους με ζώα του ίδιου είδους, κλπ).
Ο Δημόκριτος ίσως συνάντησε προσωπικά τον κατά μία δεκαετία μεγαλύτερό του Σωκράτη όταν επισκέφτηκε την Αθήνα, αλλά αργότερα “συνάντησε” και την εχθρότητα του Πλάτωνα — που ήθελε τα βιβλία του Δημόκριτου να ριχτούν στην πυρά — όπως και την εχθρική κριτική του Αριστοτέλη.
Πλάτων (~428 – ~348 π.Χ.)
 |
Ο Πλάτων ήταν κυρίως ηθικός παρά φυσικός φιλόσοφος. Κανονικά λοιπόν δεν θα συμπεριλαμβανόταν στην παρούσα ανασκόπηση αν δεν είχε διατυπώσει μια φιλοσοφική ιδέα που περιέχει πολλή “τροφή για σκέψη” και θα πρέπει πάντα να προβληματίζει τους επιστήμονες. Η ιδέα αυτή είναι η “αλληγορία του σπηλαίου”, που τη διηγείται ο Σωκράτης, και βρίσκεται στο έργο του Πλάτωνα “Πολιτεία” (επίσης γνωστού ως “Περί δικαίου”). Σύμφωνα με την αλληγορία αυτή, οι άνθρωποι είναι αλυσσοδεμένοι σε ένα σπήλαιο, έτσι ώστε να μπορούν να βλέπουν μόνο προς τα εμπρός, ποτέ προς τα πίσω. Πίσω-τους ανάβει μια φλόγα που προβάλλει τις φιγούρες των ανθρώπων στο απέναντι τοίχωμα της σπηλιάς. Οι άνθρωποι λοιπόν βλέπουν μόνο τις σκιές-τους, όχι τους πραγματικούς εαυτούς-τους, και εκλαμβάνουν τις σκιές σαν πραγματικότητα. |
Στο δεύτερο μέρος της αλληγορίας, ο Πλάτων προτείνει οτι μπορεί κάποιοι από τους ανθρώπους να λύσουν τα δεσμά-τους και να βγούν έξω από το σπήλαιο, όπου αρχικά θα τυφλωθούν από το φως του Ήλιου (που συμβολίζει την Απόλυτη Αλήθεια). Σιγά-σιγά όμως θα συνηθίσουν στο φως, και θα καταλάβουν οτι όσα έβλεπαν μέσα στο σπήλαιο δεν ήσαν παρά σκιές της πραγματικότητας. Τότε πρέπει να επιστρέψουν στο σπήλαιο και να βοηθήσουν τον υπόλοιπο κόσμο να ελευθερωθεί από τα δεσμά-του. Ίσως έτσι να συναντήσουν το μίσος όσων ανθρώπων θελήσουν να μείνουν δέσμιοι, όπως είναι, αλλά αυτοί που “έχουν δει το φως” (οι φιλόσοφοι) έχουν χρέος να προσπαθήσουν να διαφωτίσουν τους υπόλοιπους.
Αυτή την αλληγορία ο Πλάτων τη διατύπωσε για να εξηγήσει τη λειτουργία και το χρέος του φιλοσόφου στην πολιτεία. Η ιδέα όμως που είναι πολύ σημαντική από φιλοσοφική και επιστημονική άποψη είναι οτι αυτό το οποίο παρατηρούμε είναι αυτό που μεταδίδουν στον εγκέφαλό μας οι αισθήσεις-μας, μέσω των αισθητηρίων οργάνων (τα μάτια, τα αυτιά). Αν τα αισθητήρια όργανα έχουν κάποιους περιορισμούς, τότε έπεται οτι αυτά τα οποία παρατηρούμε είναι μόνο σκιές στον τοίχο του σπηλαίου, ενώ μπορεί να υπάρχει μέρος της πραγματικότητας που είναι για πάντα απλησίαστο από τον εγκέφαλό μας. Βέβαια, η ιδέα αυτή κάνει πολύ μικρή εντύπωση σε όποιον πιστεύει οτι το πνεύμα είναι υπεράνω της ύλης, και άρα μπορεί ο εγκέφαλος να έχει περιορισμούς, αλλά ο νους του ανθρώπου μπορεί πάντα να “σπάσει τα δεσμά-του και να οδηγηθεί στο φως”. Αν όμως συμβαίνει οτι το πνεύμα δεν είναι παρά ένα παράγωγο της ύλης, τότε ο νους προέρχεται από τη λειτουργία του εγκεφάλου· επομένως οι περιορισμοί του εγκεφάλου είναι και περιορισμοί του νου. Αυτή η ιδέα δείχνει να εδραιώνεται όλο και περισσότερο μεταξύ των κορυφαίων επιστημόνων της εποχής-μας.
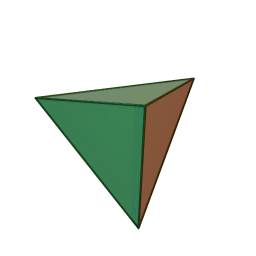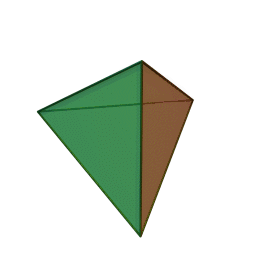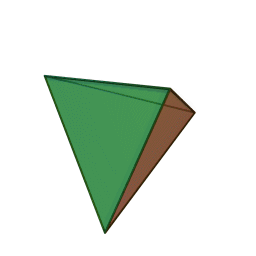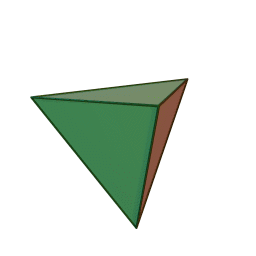
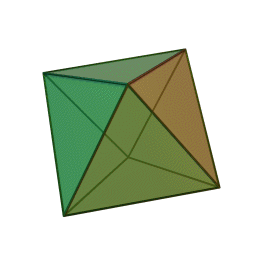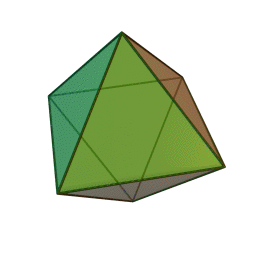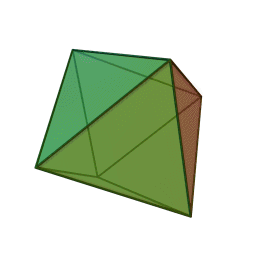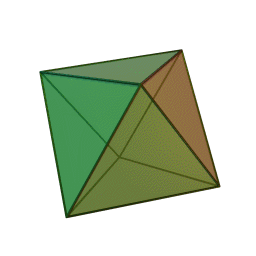
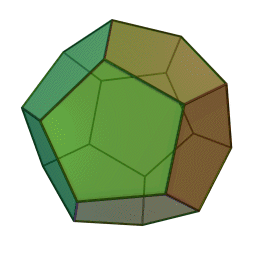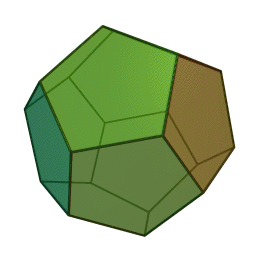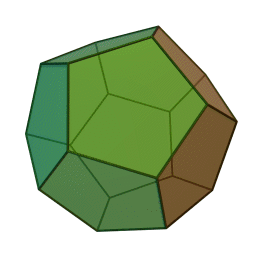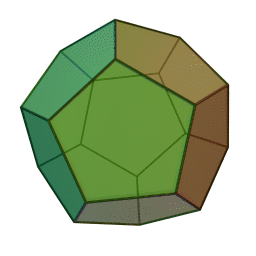
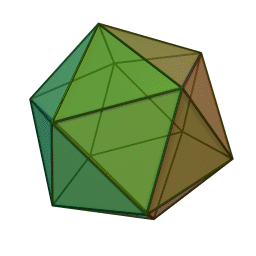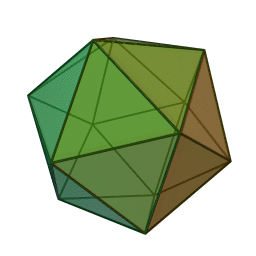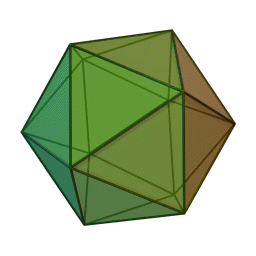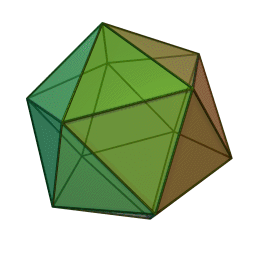
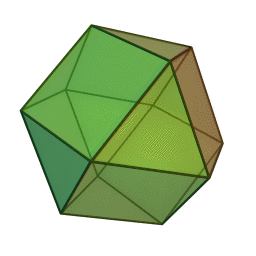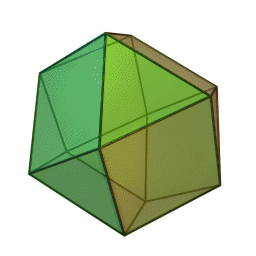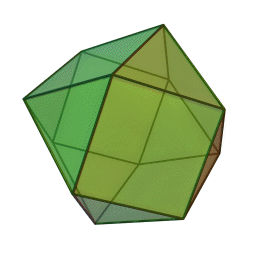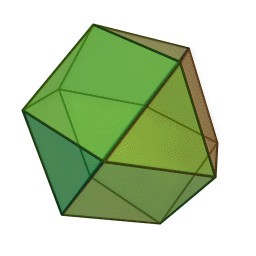
Επίσης, με το όνομα του Πλάτωνα συνδέονται τα πέντε κανονικά πολύεδρα:
|
|||||||||
| Τετράεδρο | Κύβος | Οκτάεδρο | Δωδεκάεδρο | Εικοσάεδρο | |||||
Τα πολύεδρα αυτά είναι τα μόνα “κανονικά”, και λέγονται έτσι επειδή έχουν τον ίδιο τύπο εδρών (π.χ., μόνο τετράγωνα, κλπ), ίσες ακμές, και πανομοιότυπες κορυφές. Συνήθως ονομάζονται “Πλατωνικά πολύεδρα” επειδή ο Πλάτωνας τα συσχέτισε με τα πέντε στοιχεία της φύσης (για το 5ο στοιχείο, βλ. περί Αριστοτέλη, παρακάτω).
Αριστοτέλης (384 – 322 π.Χ.)
 |
Οι φιλοσοφικές αναζητήσεις του Αριστοτέλη τον οδήγησαν σε μια εξέταση του συνόλου της γνώσης της εποχής-του. Βέβαια το ίδιο μπορεί να είχαν κάνει και άλλοι διανοητές τότε, των οποίων τα συγγράμματα δεν σώθηκαν. Ο Αριστοτέλης όμως υπήρξε τυχερός, καθώς οι ιδέες-του συμβάδιζαν σε κάποια ουσιώδη σημεία με τη χριστιανική σκέψη του Μεσαίωνα, με αποτέλεσμα τα έργα-του να διαδοθούν στη Δύση μέσω επιμελών πολλαπλών αντιγραφών, αφού είχαν νωρίτερα σωθεί μέσω αντιγραφών από τους Άραβες διανοητές, την πρώτη χιλιετία μ.Χ. Θεωρείται ο πατέρας της λογικής, η οποία σήμερα μερικές φορές ονομάζεται “Αριστοτέλεια λογική”, ενώ σαν “μαθηματική λογική” αποτελεί θεμελιώδες μάθημα στους τομείς των μαθηματικών, επιστήμης υπολογιστών, και νοολογίας. Ο Αριστοτέλης έκανε παρατηρήσεις επί του φυσικού κόσμου στους τομείς της βοτανολογίας, ζωολογίας, φυσικής, αστρονομίας, χημείας, μετεωρολογίας, και αλλού. Οι παρατηρήσεις-του όμως ήσαν ποιοτικής μάλλον, παρά ποσοτικής μορφής. Έτσι, αντικαταστάθηκαν αργότερα από τη σύγχρονη ποσοτική φυσική. |
Κάποιες από τις απόψεις-του ήσαν εντελώς λαθεμένες, όπως η άποψη οτι οι γυναίκες προέρχονται από παραμόρφωση των ανδρών, και οτι έχουν πιο λίγα δόντια από τους άντρες· ή οτι το κέντρο της ορθολογικής σκέψης βρίσκεται στην καρδιά. Άλλες απόψεις-του όμως αποδείχτηκαν σωστές, όπως π.χ. το οτι ο Ήλιος είναι μεγαλύτερος από τη Γη, και οτι η απόσταση των άστρων από τη Γη είναι πολλές φορές μεγαλύτερη από εκείνη του Ήλιου από τη Γη.
Ο Αριστοτέλης πρόσθεσε ένα πέμπτο στοιχείο στα τέσσερα του Εμπεδοκλή: τον αιθέρα, για τον οποίο είπε οτι αποτελεί την ουσία από την οποία συντίθενται τα ουράνια σώματα. Η ύπαρξη ή ανυπαρξία του αιθέρα επρόκειτο να παίξει σπουδαίο ρόλο στη φυσική του τέλους του 19ου αιώνα, και στην ανατροπή της κλασικής φυσικής του Νεύτωνα από τη σχετικιστική φυσική του Αϊνστάιν.
Έφτιαξε την πρώτη κάμερα, αποτελούμενη από ένα σκοτεινό θάλαμο και μία οπή, από την οποία περνούσε το φως του Ήλιου. Ο Αριστοτέλης παρατήρησε το είδωλο του Ήλιου στο απέναντι τοίχωμα της κάμεράς του, και σημείωσε οτι το είδωλο είναι πάντοτε κυκλικό, ανεξάρτητα από το σχήμα της οπής· όπως και οτι το είδωλο μεγαλώνει ανάλογα με την απόσταση της οπής από το τοίχωμα.
Υποστήριξε επίσης το γεωκεντρικό σύστημα, που ήθελε τη Γη στο κέντρο του σύμπαντος, και όλα τα υπόλοιπα ουράνια σώματα να περιφέρονται γύρω από αυτήν.
Αρίσταρχος ο Σάμιος (~310 – ~230 π.Χ.)
 |
Για τη ζωή του Αρίσταρχου δεν είναι γνωστά πολλά πράγματα, εκτός από το οτι γεννήθηκε στη Σάμο και οτι είχε επηρεαστεί από τις ιδέες του Φιλόλαου, ενός Πυθαγόρειου από τον Κρότωνα της Ν. Ιταλίας. Πάντως ο Αρίσταρχος μας είναι γνωστός ως ο πρώτος διανοητής που πρότεινε την ιδέα οτι ο Ήλιος είναι στο κέντρο του κόσμου, και η Γη, η Σελήνη, και οι πλανήτες περιφέρονται γύρω από αυτόν. Για τους αστέρες ο Αρίσταρχος είχε πιθανώς τη σωστή άποψη οτι βρίσκονται σε πολύ μεγαλύτερες αποστάσεις από αυτές των υπόλοιπων ουρανίων σωμάτων, και άρα δεν σχετίζονται με τα τελευταία. Έτσι μπορούμε να πούμε οτι ο Αρίσταρχος ήταν ίσως ο πρώτος που συνέλαβε την ιδέα του πλανητικού-μας συστήματος, χωρίς βέβαια να διατυπώσει ποτέ αυτόν τον όρο. Για τις απόψεις του Αρίσταρχου γνωρίζουμε μέσω του έργου του Αρχιμήδη “Άμμου Καταμέτρης” (ή “Ψαμμίτης”), το οποίο ο Αρχιμήδης απευθύνει στο βασιλιά Γέλοντα λέγοντάς του σχετικά με τον Αρίσταρχο τα εξής: |
«Εσύ [βασιλιά] γνωρίζεις οτι “κόσμος” είναι το όνομα που οι περισσότεροι αστρονόμοι δίνουν στη σφαίρα που το κέντρο-της είναι στο κέντρο της Γης, ενώ η ακτίνα-της είναι η ευθεία που ενώνει το κέντρο του Ήλιου με το κέντρο της Γης. Αυτή είναι η κοινή άποψη που έχεις ακούσει από αστρονόμους. Αλλά ο Αρίσταρχος έχει γράψει ένα βιβλίο που αποτελείται από ορισμένες υποθέσεις, όπου φαίνεται — σαν συνέπεια των υποθέσεων — οτι ο κόσμος είναι πολλές φορές μεγαλύτερος από τον “κόσμο” που μόλις ανέφερα. Οι υποθέσεις-του είναι οτι οι απλανείς αστέρες και ο Ήλιος παραμένουν ακίνητοι· οτι η Γη γυρίζει γύρω από τον Ήλιο στην περιφέρεια ενός κύκλου· οτι ο Ήλιος βρίσκεται στο κέντρο της τροχιάς αυτής· και οτι η σφαίρα των απλανών αστέρων, που έχει κέντρο ίδιο με το κέντρο του Ήλιου, είναι τόσο μεγάλη που ο κύκλος στον οποίο υποθέτει οτι η Γη περιφέρεται έχει τέτοια αναλογία με την απόσταση των απλανών αστέρων όση έχει το κέντρο της σφαίρας με την επιφάνειά της.»
Έτσι, μέσω της τεράστιας απόστασης των απλανών αστέρων, ο Αρίσταρχος εξήγησε το γιατί δεν βλέπουμε (τουλάχιστον με το μάτι) τα αστέρια να παλινδρομούν στον ουράνιο θόλο στη διάρκεια ενός έτους, φαινόμενο που ονομάζεται παράλλαξη στην αστρονομία. Η εξήγηση του Αρίσταρχου είναι σωστή, και η παράλλαξη των αστέρων γίνεται αισθητή μόνο με ακριβή όργανα μέτρησης. Πάντως η ιδέα περί ηλιοκεντρικού μοντέλου του Αρίσταρχου ξεχάστηκε τους επόμενους αιώνες, και ανασύρθηκε από τη λήθη μόνο κατά το 16ο αιώνα από τον Πολωνό αστρονόμο–ιερέα Νικόλαο Κοπέρνικο, ο οποίος έκανε αναφορά στο ηλιοκεντρικό μοντέλο του Αρίσταρχου σε μία από τις τελευταίες σελίδες του βιβλίου-του.
Αρχαίοι Έλληνες μαθηματικοί και εφευρέτες
Αρχιμήδης (~287 – ~212 π.Χ.)
Ο Αρχιμήδης, που γεννήθηκε στις Συρακούσες της Σικελίας, είναι μία από τις μεγαλύτερες μορφές στον τομέα της επιστήμης. Συγκεκριμένα, θεωρείται ένας από τους μεγαλύτερους μαθηματικούς όλων των εποχών, όπως επίσης και πολύ μεγάλος εφευρέτης.
 |
Από τα έργα του Αρχιμήδη, που δυστυχώς σώθηκαν μόνο λίγα (ενώ τέσσερα απ’ αυτά ανακαλύφθηκαν μόλις το 1906, στον “παλίμψηστο του Αρχιμήδη”), γνωρίζουμε οτι ασχολήθηκε με πολλά προβλήματα γεωμετρίας, τα οποία έλυσε με ιδιοφυείς μεθόδους. Ένα από τα προβλήματα αυτά ήταν ο προσεγγιστικός υπολογισμός του αριθμού π. Ο Αρχιμήδης έλυσε το πρόβλημα αυτό υπολογίζοντας το εμβαδό διάφορων πολυγώνων που είναι εγγεγραμμένα και περιγεγραμμένα σε κύκλο (βλ. σχήμα, παρακάτω). Έτσι, βρήκε οτι η τιμή του π πρέπει να βρίσκεται μεταξύ του 31⁄7 και του 310⁄71, δηλαδή μεταξύ των τιμών 3,1428 και 3,1408. Πράγματι, η τιμή του π είναι περίπου 3,1416. Για τη λύση κάποιων προβλημάτων χρησιμοποίησε τρόπους που θυμίζουν τις μεθόδους του απειροστικού λογισμού, ο οποίος αναπτύχθηκε κατά το 17ο αιώνα. Ο Αρχιμήδης προηγήθηκε κατά περίπου 19 αιώνες. |
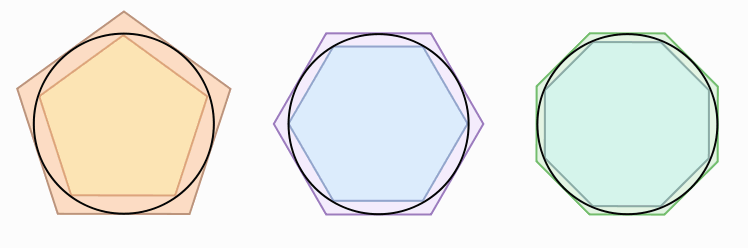
Πολύγωνα εγγεγραμμένα και περιγεγραμμένα σε κύκλο που χρησιμοποίησε ο Αρχιμήδης για τον υπολογισμό του αριθμού π
Όπως βεβαιώνει ο Ρωμαίος ρήτωρ και φιλόσοφος Κικέρων, που ανακάλυψε τον τάφο του Αρχιμήδη στη Σικελία σχεδόν έναν αιώνα μετά το θάνατο του επιστήμονα, πάνω στην πλάκα του τάφου ήταν χαραγμένο το σχήμα ενός γεωμετρικού θεωρήματος που απέδειξε ο Αρχιμήδης· συγκεκριμένα οτι ο όγκος σφαίρας είναι ίσος με τα 2⁄3 του όγκου του κυλίνδρου που την περικλείει (βλ. σχήμα).
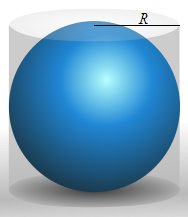
Όγκος σφαίρας = 2⁄3 όγκου περιγεγραμμένου κυλίνδρου
Αυτό το συμπέρασμα του Αρχιμήδη μας επιτρέπει να υπολογίσουμε τον όγκο της σφαίρας, γιατί ο όγκος του κυλίνδρου είναι γνωστός και ίσος με βάση x ύψος, όπου η βάση του κυλίνδρου είναι πR2, και το ύψος ίσο με 2R (όπου R η ακτίνα της σφαίρας). Άρα ο όγκος του κυλίνδρου είναι 2πR3, και της σφαίρας τα 2⁄3 αυτού, δηλαδή 4⁄3πR3. Πράγματι, αυτός είναι ο τύπος του όγκου σφαίρας ακτίνας R.
Ο Αρχιμήδης σε ένα από τα έργα-του, το “Άμμου Καταμέτρης” (ή “Ψαμμίτης”, βλ. προηγούμενη ενότητα περί Αρίσταρχου) επινόησε μια μέθοδο για την έκφραση πολύ μεγάλων αριθμών. Στο έργο αυτό επιχείρησε να βρει τον αριθμό των κόκκων άμμου που θα απαιτούνταν για να γεμίσει μια σφαίρα που θα περιέκλειε το σύμπαν, ανάλογα με τις διαστάσεις που αποδίδονταν στο σύμπαν τότε. Ο μεγαλύτερος αριθμός που ονόμασε με τη μέθοδό του ο Αρχιμήδης ήταν ο 108·1016, δηλαδή το 1 ακολουθούμενο από 80 τετράκις εκατομμύρια μηδενικά. Αν γράφαμε τον αριθμό αυτόν ολογράφως σαν 1000...000, με τα μηδενικά το ένα πίσω από το άλλο, και το καθένα να χρειάζεται 2 χιλιοστά για να τυπωθεί, τότε το μήκος του αριθμού αυτού θα ήταν ίσο με 1067 φορές την απόσταση Ήλιου – Γης, ή 35,4 φορές την απόσταση Ήλιου – Ποσειδώνα.
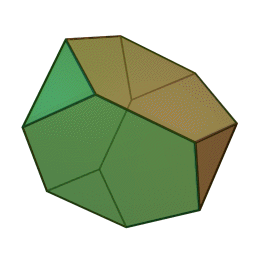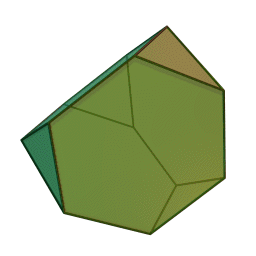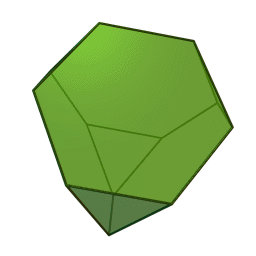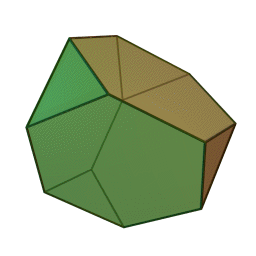
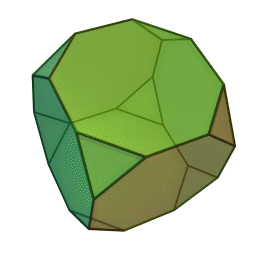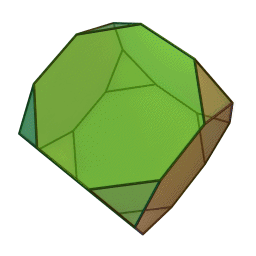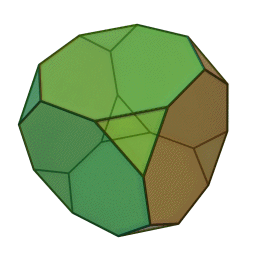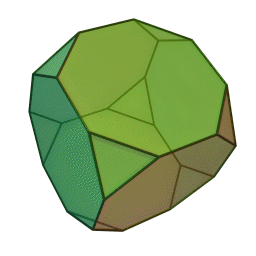
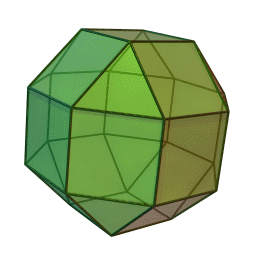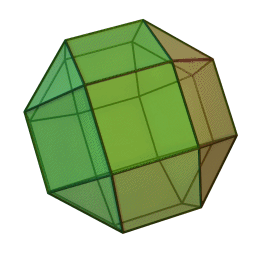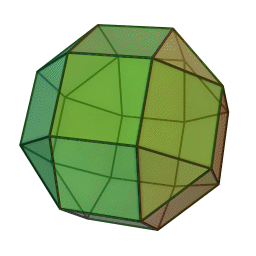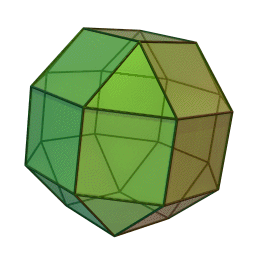
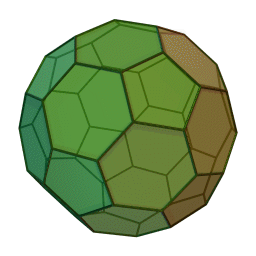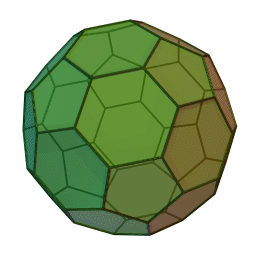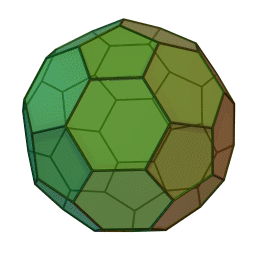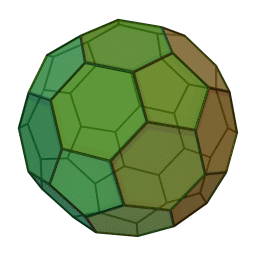
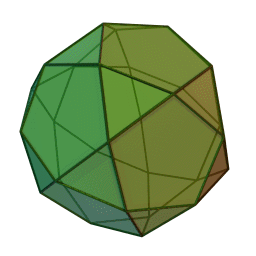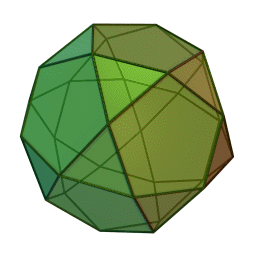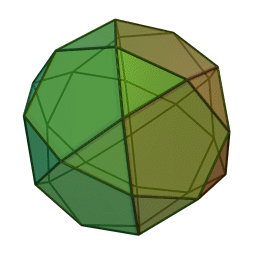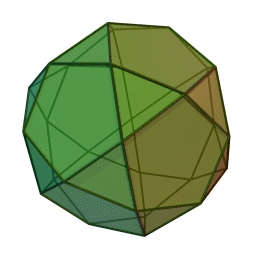
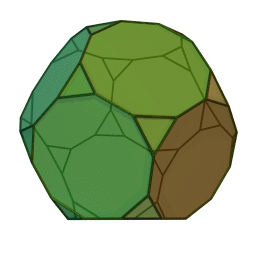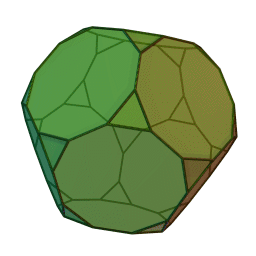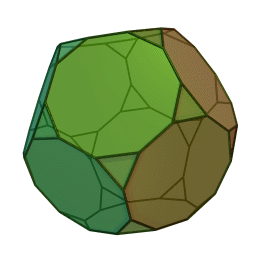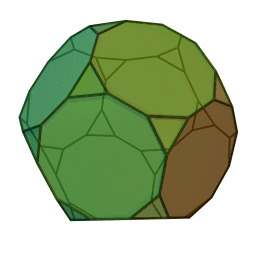
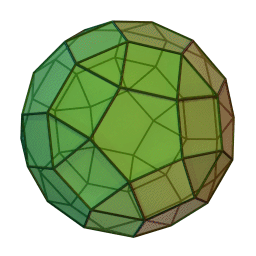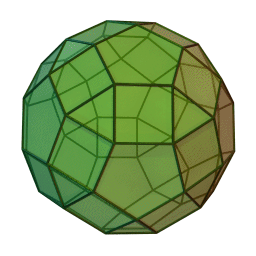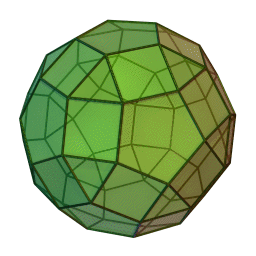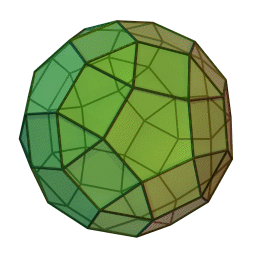
Στη στερεομετρία, τα λεγόμενα “ημικανονικά πολύεδρα” ονομάζονται και “Αρχιμήδεια πολύεδρα”, γιατί τα περιέγραψε ο Αρχιμήδης σ’ ένα έργο-του που δεν διασώθηκε.
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
Τα πολύεδρα αυτά λέγονται “ημικανονικά” γιατί ενώ έχουν ίσες ακμές και πανομοιότυπες κορυφές, εντούτοις, σε αντίθεση με τα “κανονικά” ή “Πλατωνικά” πολύεδρα (βλ. εδάφιο περί Πλάτωνα), έχουν περισσότερα από ένα είδη εδρών (π.χ., τόσο τρίγωνα όσο και τετράγωνα, κλπ). Πάντως όλες οι έδρες-τους είναι κανονικά πολύγωνα. Είναι ακριβώς τα παραπάνω 13, δηλ. δεν υπάρχουν άλλα.
Εκτός από μαθηματικός όμως, ο Αρχιμήδης υπήρξε επίσης και μεγάλος εφευρέτης.
Σύμφωνα με μια ιστορία που αναφέρει ο Ρωμαίος συγγραφέας και αρχιτέκτονας Βιτρούβιος (Vitruvius), ο βασιλιάς Ιέρων ο 2ος έλαβε σαν δώρο ένα χρυσό στεφάνι, το οποίο όμως δεν ήξερε αν ήταν όλο από χρυσό ή ήταν κράμα χρυσού με άλλα μέταλλα, όπως χαλκό ή ασήμι. Ο Ιέρων ζήτησε από τον Αρχιμήδη να λύσει αυτό το πρόβλημα, χωρίς βέβαια να καταστρέψει το στεφάνι. Λέγεται οτι ο Αρχιμήδης εμπνεύστηκε τη λύση καθώς έκανε το λουτρό-του, παρατηρώντας τον όγκο του νερού που εκτόπιζε το σώμα-του.
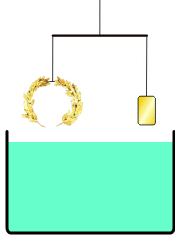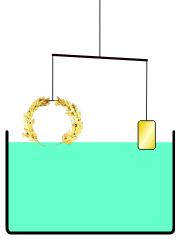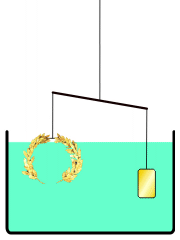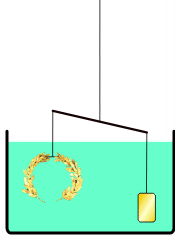
Λύση προβλήματος καθαρότητας χρυσού αντικειμένου ακανόνιστου σχήματος
Το παραπάνω σχήμα δείχνει την αρχή που ακολουθείται για τη λύση. Αρχικά το στεφάνι ζυγίζεται και δημιουργείται ένα αντικείμενο από καθαρό χρυσό (τα “σταθμά”) με ακριβώς ίσο βάρος. Τα σταθμά και το στεφάνι τοποθετούνται στα δύο άκρα ζυγαριάς. Καθώς τα δύο άκρα του ζυγού βυθίζονται σε νερό, αν το στεφάνι δεν είναι από καθαρό χρυσό, τότε η άνωση του νερού θα κάνει το ζυγό να γείρει προς το μέρος των σταθμών, ενώ αν είναι από καθαρό χρυσό τότε η ισορροπία θα παραμείνει. Λέγεται οτι όταν ο Αρχιμήδης ανακάλυψε τη λύση, βγήκε όπως ήταν χωρίς ρούχα από το λουτρό και φώναζε στους δρόμους των Συρακουσών: «Εὕρηκα! Εὕρηκα!»
Σαν εφευρέτης ο Αρχιμήδης πιστώνεται με πολλές εφευρέσεις, κάποιες πρακτικές, ενώ άλλες προς χρήση σε πολεμικές συγκρούσεις. Γνωστός είναι π.χ. ο “κοχλίας του Αρχιμήδη” (βλ. σχήμα), ο οποίος χρησιμοποιείται ακόμη και σήμερα σε μέρη της Αιγύπτου και της Λιβύης για άντληση νερού από πηγάδια.
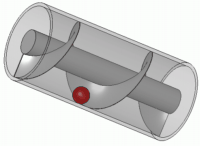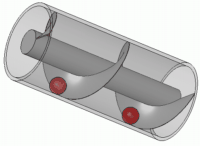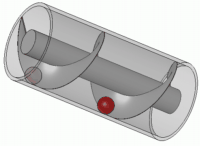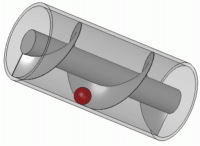
Λέγεται ακόμη οτι ο Αρχιμήδης βοήθησε στην καταστροφή του στόλου των Ρωμαίων κατά την πολιορκία των Συρακουσών (214–212 π.Χ.) εστιάζοντας έναν αριθμό από μεγάλα κάτοπτρα στα πλοία των Ρωμαίων, και καίγοντάς τα με τις ακτίνες του Ήλιου. Αυτή η ιστορία όμως δεν είναι βέβαιο οτι είναι αληθινή. Έχουν γίνει πειράματα για την επαλήθευσή της, αλλά χωρίς θετικά αποτελέσματα, καθώς διαπιστώθηκε οτι θα χρειαζόταν το ξύλινο ομοίωμα πλοίου να μείνει ακίνητο για αρκετά λεπτά προκειμένου να αναφλεγεί. Ο Αρχιμήδης τελικά φονεύθηκε από Ρωμαίο στρατιώτη κατά την κατάληψη των Συρακουσών με τη λήξη εκείνου του πολέμου, όταν ο στρατιώτης, παραβαίνοντας την εντολή του Ρωμαίου στρατηγού Μάρκελλου να μη φονευθεί ο Αρχιμήδης, τον σκότωσε καθώς ο Αρχιμήδης ήταν απασχολημένος στο σπίτι-του με τη λύση κάποιου προβλήματος. Σύμφωνα με την ιστορία, ο Αρχιμήδης είπε στο Ρωμαίο στρατιώτη: «Μὴ μου τοὺς κύκλους τάραττε!» («Μη μου χαλάς τους κύκλους» — που είχε χαραγμένους στο έδαφος), πριν ο στρατιώτης τον σκοτώσει — ιστορία που ανήκει μάλλον στην περιοχή του μύθου.
Ερατοσθένης (~276 – ~195 π.Χ.)
 |
Ο Ερατοσθένης γεννήθηκε στην Κυρήνη της Βόρειας Αφρικής (σημερινή ανατολική Λιβύη), και έζησε κυρίως στην Αλεξάνδρεια της Αιγύπτου. Ήταν αυτός που εισήγαγε τον όρο “γεωγραφία”, και κατά τη διάρκεια της ζωής-του έκανε πολλές γεωγραφικές μετρήσεις, κάποιες από τις οποίες είχαν εκπληκτική ακρίβεια για τα δεδομένα εκείνης της εποχής. Για παράδειγμα, υπολόγισε την περιφέρεια της Γης, και τη βρήκε ίση με 252.000 στάδια. Αν με “στάδιο” εννοούσε το μήκος που χρησιμοποιούσαν τότε στην Αίγυπτο (157,5 μέτρα), τότε η περιφέρεια γίνεται ίση με 39.690.000 μέτρα, που είναι με πολύ μεγάλη ακρίβεια παρόμοια με την αληθινή τιμή: 40.007.860 μ., δηλαδή έπεσε έξω μόνο κατά 318 χιλιόμετρα, ή 8 τοις χιλίοις. Υπολόγισε, επίσης με εντυπωσιακή ακρίβεια, την κλίση του άξονα της Γης, και πιθανώς και την απόσταση της Γης από τον Ήλιο. |
Στον τομέα των μαθηματικών, ο Ερατοσθένης είναι γνωστός για το περίφημο “κόσκινο του Ερατοσθένη”, έναν αλγόριθμο (μέθοδο) για τον υπολογισμό των πρώτων αριθμών. Ένας αριθμός ονομάζεται “πρώτος” όταν δεν διαιρείται ακριβώς από κανέναν άλλον αριθμό εκτός από τη μονάδα και τον εαυτό-του. Π.χ. ο 5 είναι πρώτος, γιατί διαιρείται ακριβώς μόνο από το 1 και το 5, ενώ ο 4 δεν είναι πρώτος, γιατί διαιρείται από το 2 ακριβώς (δηλαδή η διαίρεση αφήνει υπόλοιπο μηδέν).

Το κόσκινο του Ερατοσθένη λειτουργεί σύμφωνα με τα ακόλουθα βήματα 1–4 (βλ. και εικόνα, παραπάνω):
-
Γράφουμε ολους τους ακέραιους αριθμούς στη σειρά, μέχρι το μέγιστο που επιθυμούμε να χαρακτηρίσουμε ως πρώτο ή μη-πρώτο. (Στην παραπάνω εικόνα, μέχρι το 120.) Ξεκινάμε από το 2, γιατί ο 1 είναι εξ ορισμού ούτε πρώτος ούτε μη-πρώτος.
-
Ο πρώτος στη σειρά αριθμός που δεν έχει διαγραφεί ακόμα είναι πρώτος. (Διαγραφές γίνονται στο επόμενο βήμα.)
-
Διαγράφουμε από τη λίστα όλα τα πολλαπλάσια του πρώτου που μόλις βρήκαμε.
-
Επιστρέφουμε στο βήμα 2.
Έτσι, την πρώτη φορά που πηγαίνουμε στο βήμα 2, ο πρώτος αριθμός στη λίστα είναι ο 2. Άρα αυτός είναι πρώτος. Μετά, στο βήμα 3 διαγράφουμε όλα τα πολλαπλάσια του 2 (δηλ. τους άρτιους αριθμούς), και όταν επιστρέφουμε στο βήμα 2 βρίσκουμε σαν πρώτο στη λίστα τον 3· άρα κι αυτός είναι πρώτος. Μετά διαγράφουμε τα πολλαπλάσια του 3, και επιστρέφοντας βρίσκουμε σαν πρώτο αριθμό στη λίστα τον 5· άρα κι ο 5 είναι πρώτος· κ.ο.κ.
Η Ευκλείδεια γεωμετρία, και η σημασία-της στο οικοδόμημα της επιστήμης
Η γεωμετρία άρχισε να αναπτύσσεται αρχικά στη Μέση Ανατολή και στην Αίγυπτο, αλλά μόνο για πρακτκούς σκοπούς, όπως ήδη αναφέρθηκε στην εισαγωγή. Στην Ελλάδα εισήχθη η αποδεικτική μέθοδος, που — επίσης όπως ήδη αναφέρθηκε — μας καθιστά 100% βέβαιους για τα συμπεράσματα που συνάγουμε. Ας δούμε ένα απλούστατο παράδειγμα μαθηματικής απόδειξης.
Κάθε απόδειξη ξεκινάει από κάποιες υποθέσεις, και με χρήση της λογικής, καταλήγει σε κάποιο συμπέρασμα. Στη γεωμετρία, οι πρωταρχικές υποθέσεις που γίνονται δεκτές χωρίς περαιτέρω απόδειξη (γιατί από κάπου πρέπει να ξεκινήσει κανείς) λέγονται αξιώματα, ενώ το συμπέρασμα λέγεται θεώρημα. Ιδού ένα παράδειγμα θεωρήματος που αποδεικνύεται βάσει ενός αξιώματος:
|
Αξίωμα: Από δύο διαφορετικά σημεία διέρχεται μία και μόνο μία ευθεία γραμμή. Θεώρημα: Δύο διαφορετικές ευθείες μπορούν να τέμνονται μόνο σε το πολύ ένα σημείο. |
Το ερώτημα είναι πώς αποδεικνύουμε το θεώρημα βασιζόμενοι στο αξίωμα. Σκεφτόμαστε λογικά, ως εξής: Ας υποθέσουμε οτι, αντίθετα με το θεώρημα, δύο διαφορετικές ευθείες Ε1 και Ε2 μπορούν να τέμνονται σε περισσότερα από ένα σημεία — ας τα πούμε Σ1 και Σ2. Άρα τόσο η Ε1 όσο και η Ε2 διέρχονται από τα Σ1 και Σ2. Όμως αυτό είναι αντίθετο με το αξίωμα, που λέει οτι από τα δύο σημεία Σ1 και Σ2 μπορεί να διέρχεται μία και μόνο μία ευθεία γραμμή, όχι δύο. Άρα η υπόθεση που κάναμε (οτι δηλαδή δύο διαφορετικές ευθείες μπορούν να τέμνονται σε περισσότερα από ένα σημεία), που ήταν αντίθετη του θεωρήματος, δεν είναι σωστή. Άρα είναι σωστή η αντίθετή της, που είναι ακριβώς το θεώρημα που θέλαμε να αποδείξουμε.
Η παραπάνω απόδειξη χρησιμοποιεί τη μέθοδο της “εις άτοπο απαγωγής”· δηλαδή, υποθέτουμε το αντίθετο αυτού που θέλουμε να αποδείξουμε, βρίσκουμε οτι αυτό δεν είναι δυνατό (καταλήγουμε σε άτοπο), άρα συμπεραίνουμε αυτό που θέλουμε να αποδείξουμε.
Τα πέντε αιτήματα του Ευκλείδη είναι τα εξής:
| Αίτημα 1ο: ᾿Ηιτήσθω ἀπὸ παντὸς σημείου ἐπὶ πᾶν σημεῖον εὐθεῖαν γραμμὴν ἀγαγεῖν. Δηλαδή: Έστω οτι από κάθε σημείο προς κάθε σημείο είναι δυνατό να φερθεί ευθεία. |
| Αίτημα 2ο: Καὶ πεπερασμένην εὐθεῖαν κατὰ τὸ συνεχὲς ἐπ’ εὐθείας ἐκβαλεῖν. Και μία πεπερασμένη ευθεία μπορεί να προεκταθεί συνεχώς σε ευθεία κατεύθυνση. |
| Αίτημα 3ο: Καὶ παντὶ κέντρῳ καὶ διαστήματι κύκλον γράφεσθαι. Και με κάθε κέντρο και διάστημα γράφεται κύκλος. |
| Αίτημα 4ο: Καὶ πάσας τὰς ὀρθὰς γωνίας ἴσας ἀλλήλαις εἶναι. Και όλες οι ορθές γωνίες είναι ίσες μεταξύ-τους. |
Τέλος, ακολουθεί το περίφημο πέμπτο αίτημα του Ευκλείδη, που θα δούμε αργότερα ποιο ρόλο έπαιξε κατά το 19ο – 20ό αιώνα:
| Αίτημα 5ο: Καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλομένας τὰς δύο εὐθείας ἐπ’ ἄπειρον συμπίπτειν ἐφ’ ἃ μέρη εἰσὶν αἱ τῶν δύο ὀρθῶν ἐλάσσονες. Και αν ευθεία τέμνει δύο ευθείες και κάνει τις εντός και επί τα αυτά μέρη γωνίες μικρότερες των δύο ορθών, τότε προεκτεινόμενες οι δύο ευθείες επ’ άπειρον τέμνονται στη μεριά όπου είναι οι γωνίες οι μικρότερες των δύο ορθών. |
Όπως βλέπουμε, το 5ο αίτημα ακούγεται πολύπλοκο. Σχηματικά, το καταλαβαίνουμε στο παρακάτω διάγραμμα:
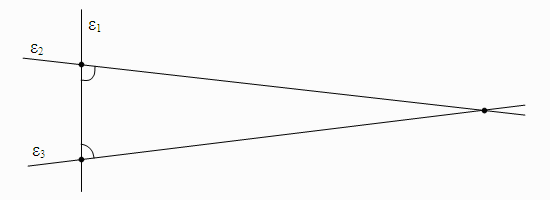
Η ε1 είναι η ευθεία που «τέμνει δύο ευθείες» (τις ε2 και ε3). Εφόσον το άθροισμα των δύο γωνιών (που είναι σημειωμένες με τις μικρές κυρτές γραμμές) είναι μικρότερο από δύο ορθές γωνίες, το 5ο αίτημα λέει οτι οι ε2 και ε3 θα πρέπει να τέμνονται προς τη ίδια πλευρά της ε1 όπου βρίσκονται και οι γωνίες.
Η σημασία της Ευκλείδειας γεωμετρίας για την επιστήμη είναι διπλή.
Πρώτα-πρώτα, μέσω της γεωμετρίας γαλουχήθηκαν στην ορθολογική σκέψη εκατομμύρια νέοι στο Δυτικό κόσμο και πολιτισμό. Όταν εκπαιδεύεται κανείς στη γεωμετρία, δεν μαθαίνει επιφανειακά τα θεωρήματα και τις αποδείξεις-τους μόνο, αλλά εμπεδώνει σε ένα βαθύτερο (πιο αφηρημένο) επίπεδο τον ορθολογικό τρόπο σκέψης, δηλαδή της λογικής εξαγωγής συμπερασμάτων βάσει των δεδομένων υποθέσεων. Η Ευκλείδεια γεωμετρία είναι εξαιρετικό εργαλείο για το σκοπό αυτό.
Και δεύτερο, η Ευκλείδεια γεωμετρία περιγράφει τον κόσμο έτσι όπως μας τον παρουσιάζουν οι αισθήσεις-μας. Δηλαδή, ο κόσμος στον οποίο ζούμε δεν είναι ακριβώς Ευκλείδειος στην πραγματικότητα, αλλά μόνο κατά προσέγγιση Ευκλείδειος. (Εδώ ας θυμηθούμε και την Αλληγορία του Σπηλαίου, του Πλάτωνα: οι αισθήσεις μας παρουσιάζουν μόνο σκιές από την πραγματικότητα στον τοίχο του σπηλαίου.) Αυτό που συνέβει λοιπόν στην επιστήμη είναι οτι αναπτύχθηκε μια ολόκληρη φυσική θεωρία, η λεγόμενη Κλασική Μηχανική, ή Νευτώνεια φυσική, που έμμεσα προϋποθέτει έναν Ευκλείδειο κόσμο (συγκεκριμένα έναν κόσμο όπου ο χρόνος είναι κάτι το ξεχωριστό, ανεξάρτητο από το χώρο). Όταν όμως τα δεδομένα από τις όλο και πιο λεπτομερείς παρατηρήσεις άρχισαν να διαφωνούν με το μοντέλο του Ευκλείδειου κόσμου, έγινε η “επανάσταση” στη φυσική μέσω της θεωρίας της σχετικότητας, του Αϊνστάιν, όπου απορρίφθηκε το Ευκλείδειο μοντέλο για τον κόσμο και χρησιμοποιήθηκαν άλλα μοντέλα, από μη-Ευκλείδειες γεωμετρίες που είχαν ήδη αναπτυχθεί κατά το 19ο αιώνα. (Στη σχετικιστική γεωμετρία ο χρόνος δεν είναι ανεξάρτητος του χώρου, αλλά κάθε χρονικό διάστημα εμπεριέχει ένα χωρικό, και αντίστροφα: κάθε χωρικό διάστημα εμπεριέχει ένα χρονικό. Έτσι μιλάμε για το χωροχρόνο σαν ένα “τετραδιάστατο συνεχές”.) Η πορεία επομένως της γεωμετρικής σκέψης βάδισε παράλληλα με εκείνη της φυσικής, και κατ’ επέκταση και της επιστημονικής σκέψης, καθώς η φυσική βρίσκεται πάντα στο κέντρο, στην κατ’ εξοχήν “καρδιά” της επιστήμης.
Σημειώσεις:
(^) Ο Ηράκλειτος ο Ομηρικός δεν πρέπει να συγχέεται με τον Ηράκλειτο τον Εφέσιο. Ο πρώτος έκανε αναφορά στο έργο του δεύτερου, και είναι αυτός που έγραψε οτι, σύμφωνα με τον Ηράκλειτο τον Εφέσιο, «μέσα στον ίδιο ποταμό μπαίνουμε και δεν μπαίνουμε, είμαστε και δεν είμαστε».
Πίσω στη γενική σελίδα του Διαδικτυακού Επιστημονικού Πανεπιστημίου