 |
Επιστημονική Μέθοδος και ΠαραδοχέςΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ Ε1 ΤΟΥ Δ.Ε.Π.
|
Στόχος και ποιόν του μαθήματος
Στο παρόν μάθημα θα εξετάσουμε τα θεμέλια αυτού που ονομάζουμε “επιστήμη”, αλλά με την έννοια της λέξης που εξηγεί η αμέσως επόμενη ενότητα. Υπόψη οτι το μάθημα αυτό, παρόλο που εξετάζει θεμελιώδεις έννοιες της επιστήμης, δεν είναι επιστημονικό αλλά φιλοσοφικό. Δεν θα μπορούσε να συμβαίνει διαφορετικά άλλωστε. Τα θεμέλια ενός τομέα δεν μπορούν να μπουν μέσα από τον ίδιο τον τομέα, γιατί κάτι τέτοιο θα οδηγούσε σε μια λογικά αστήρικτη, κυκλική κατασκευή· τα θεμέλια βρίσκονται υποχρεωτικά έξω από τον τομέα. Γιαυτό λοιπόν τα θεμέλια της επιστήμης δεν είναι επιστημονικά, αλλά φιλοσοφικά.
Με τί ασχολείται η σημερινή επιστήμη
Στην αρχαία ελληνική γλώσσα η λέξη “επιστήμη” σήμαινε γενικά τη γνώση. Σήμαινε επίσης και την εξειδικευμένη γνώση, όπως π.χ. εκείνη της πολεμικής τέχνης (έτσι χρησιμοποιεί τη λέξη για παράδειγμα ο Θουκυδίδης), και ακόμα και σήμερα μπορούμε να τη χρησιμοποιήσουμε με τον ίδιο τρόπο (π.χ. όταν λέμε: «Α, το τάβλι είναι ολόκληρη επιστήμη!»). Η λέξη αυτή, όπως και τόσες άλλες ελληνικές, πέρασε στη λατινική γλώσσα, και από εκεί έγινε κτήμα των Δυτικοευρωπαϊκών γλωσσών, ιδίως όσων είναι άμεσοι ή έμμεσοι απόγονοι της λατινικής. Έτσι, στα αγγλικά λόγου χάρη, το επίθετο “epistemic” σημαίνει «αυτό που σχετίζεται με τη γνώση»· και “epistemology” είναι «ο κλάδος της φιλοσοφίας που ασχολείται με τη γνώση, τις αρχές, τη θεμελίωση, το εύρος, και την ορθότητά της» (μετάφραση του λήμματος epistemology από το American Heritage Dictionary).
Παράλληλα όμως με την ελληνική ρίζα epistem-, στη λατινική χρησιμοποιήθηκε και η λέξη “scientia”, επίσης αρχικά με την ίδια έννοια, δηλαδή τη γνώση. Αλλά όπως συμβαίνει πολύ συχνά στις γλώσσες, το scientia — από το οποίο προήλθε το αγγλικό “science” — στην πορεία των αιώνων, και ιδίως στην πορεία της εξέλιξης της γνώσης, πήρε ελαφρώς διαφορετική χροιά, δηλαδή απέκτησε κάπως διαφορετικό νόημα. Σήμερα λοιπόν, το αγγλικό science δεν σημαίνει γενικά και αόριστα τη γνώση περί του οτιδήποτε, αλλά τη γνώση περί του φυσικού κόσμου, και ιδίως γνώση που αποκτάται ακολουθώντας μια συγκεκριμένη μέθοδο, την επιστημονική μέθοδο (την οποία θα εξετάσουμε στην αμέσως επόμενη ενότητα).
Αυτός είναι ο σκοπός του παρόντος μαθήματος· να εξετάσουμε δηλαδή τα
θεμέλια της επιστήμης, αλλά με την έννοια του αγγλικού science,
όχι με την έννοια που δίνουμε στη λέξη αυτή στην ελληνική. Και επειδή
στα ελληνικά έχουμε ήδη τη λέξη “γνώση”, θα ήταν χρήσιμο να προσδώσουμε
και στη γλώσσα-μας το ίδιο νόημα στη λέξη “επιστήμη” όπως αυτό που έχει
η αγγλική λέξη “science” — αφού είναι πλεονασμός να χρησιμοποιούμε δύο
λέξεις (γνώση και επιστήμη) εννοώντας περίπου το ίδιο πράγμα. Βέβαια δεν
εννούμε ακριβώς το ίδιο πράγμα. Μπορεί π.χ. να έχω γνώση του
γεγονότος οτι η Μαρία παντρεύτηκε το Γιώργο, αλλά αυτό δεν έχει καμιά
σχέση με επιστήμη. Θεωρούμε όμως στην Ελλάδα οτι ότι διδάσκεται στο
πανεπιστήμιο, συμπεριλαμβανομένων τομέων όπως η θεολογία και η νομική,
είναι επιστήμη, παρόλο που οι διδάσκοντες και διδασκόμενοι στους
συγκεκριμένους τομείς συνήθως έχουν πλήρη άγνοια της επιστημονικής
μεθόδου και των παραδοχών της επιστήμης. Ο δικηγόρος, παραδείγματος χάρη
όπως θα δούμε, είναι ένας τεχνίτης του λόγου και της μνήμης![]() ·
συμβαίνει όμως οτι συγχέουμε την ικανότητα που έχει αποκτήσει με πολύ
κόπο και μετά από πολλά χρόνια σπουδών και πρακτικής εξάσκησης με την
έννοια της επιστήμης, επειδή ο δικηγόρος εκπαιδεύεται στο παν·επιστήμ·ιο,
λέξη που μας ωθεί στο να πιστεύουμε οτι κάθε τί που διδάσκεται εκεί
είναι μέρος της επιστήμης (με την έννοια “science”). Εφόσον οι
επιστημονικές επιρροές και η τεχνολογία εξακολουθούν να μας έρχονται
κυρίως από τη Δύση, κ’ εφόσον η αγγλική γλώσσα εξακολουθεί να κυριαρχεί
παγκόσμια, καλό είναι να γνωρίζουμε οτι με τον όρο “scientist” οι
ομιλητές της αγγλικής δεν εννοούν τον δικηγόρο, το θεολόγο, ή το
φιλόσοφο, αλλά το φυσικό, το χημικό, το βιολόγο, τον αστρονόμο, το
γεωλόγο, το μετεωρολόγο, και όσους άλλους επιστήμονες ασχολούνται με το
φυσικό κόσμο. Βέβαια το τί είναι ακριβώς “φυσικός κόσμος” δεν είναι και
τόσο προφανές. Για παράδειγμα, επιστήμη είναι και η γλωσσολογία, παρόλο
που ασχολείται με τη γλώσσα, μια αφηρημένη και όχι “χειροπιαστή” έννοια,
αλλά προϊόν ενός φυσικού όντος, του ανθρώπου· επιστήμη είναι τα
μαθηματικά, ασχολούμενα με την έννοια “αριθμός”, προϊόν αφαίρεσης
ιδιοτήτων του φυσικού κόσμου, μια αφαίρεση που γίνεται από τον ανθρώπινο
νου· επιστήμη είναι ακόμη η νοολογία, που ασχολείται
ακριβώς με το νου (στην αφηρημένη-του εκδοχή, όχι απλώς με το φυσικό
αντικείμενο που υλοποιεί ένα νου, δηλαδή τον εγκέφαλο).
·
συμβαίνει όμως οτι συγχέουμε την ικανότητα που έχει αποκτήσει με πολύ
κόπο και μετά από πολλά χρόνια σπουδών και πρακτικής εξάσκησης με την
έννοια της επιστήμης, επειδή ο δικηγόρος εκπαιδεύεται στο παν·επιστήμ·ιο,
λέξη που μας ωθεί στο να πιστεύουμε οτι κάθε τί που διδάσκεται εκεί
είναι μέρος της επιστήμης (με την έννοια “science”). Εφόσον οι
επιστημονικές επιρροές και η τεχνολογία εξακολουθούν να μας έρχονται
κυρίως από τη Δύση, κ’ εφόσον η αγγλική γλώσσα εξακολουθεί να κυριαρχεί
παγκόσμια, καλό είναι να γνωρίζουμε οτι με τον όρο “scientist” οι
ομιλητές της αγγλικής δεν εννοούν τον δικηγόρο, το θεολόγο, ή το
φιλόσοφο, αλλά το φυσικό, το χημικό, το βιολόγο, τον αστρονόμο, το
γεωλόγο, το μετεωρολόγο, και όσους άλλους επιστήμονες ασχολούνται με το
φυσικό κόσμο. Βέβαια το τί είναι ακριβώς “φυσικός κόσμος” δεν είναι και
τόσο προφανές. Για παράδειγμα, επιστήμη είναι και η γλωσσολογία, παρόλο
που ασχολείται με τη γλώσσα, μια αφηρημένη και όχι “χειροπιαστή” έννοια,
αλλά προϊόν ενός φυσικού όντος, του ανθρώπου· επιστήμη είναι τα
μαθηματικά, ασχολούμενα με την έννοια “αριθμός”, προϊόν αφαίρεσης
ιδιοτήτων του φυσικού κόσμου, μια αφαίρεση που γίνεται από τον ανθρώπινο
νου· επιστήμη είναι ακόμη η νοολογία, που ασχολείται
ακριβώς με το νου (στην αφηρημένη-του εκδοχή, όχι απλώς με το φυσικό
αντικείμενο που υλοποιεί ένα νου, δηλαδή τον εγκέφαλο).
Ας σημειωθεί οτι η ζητούμενη εξειδίκευση της λέξης “επιστήμη”, ώστε από γενική γνώση να σημαίνει ειδικά τη γνώση του φυσικού κόσμου που αποκτάται μέσω της επιστημονικής μεθόδου, είναι κάτι που παρατηρείται πολύ συχνά στη γλώσσα. Όταν μια έννοια γίνεται πιο πολύπλοκη μέσω της συσσώρευσης γνώσης, η αρχικά χρησιμοποιούμενη λέξη για την έννοια αυτή συνήθως εξειδικεύεται. Παράδειγμα η λέξη μύθος, που στην αρχαία-μας γλώσσα σήμαινε γενικά το λόγο (οποιασδήποτε μορφής), αλλά στην πορεία των αιώνων εξειδικεύτηκε ώστε να σημαίνει τη φανταστική ιστορία, την εξωπραγματική και ιδίως τη λανθασμένη ιστορία (π.χ.: «Αυτό είναι σκέτος μύθος», ή «μυθεύματα»), καθώς έγινε κατανοητό οτι οι αρχαίοι “μύθοι” ήσαν όλοι προϊόντα της ανθρώπινης φαντασίας. Άλλο παράδειγμα είναι η λέξη τέχνη, που ενώ έχει το γνωστό νόημα στη σύγχρονη γλώσσα (καλή τέχνη, όπως ζωγραφική, γλυπτική, μουσική, υποκριτική, κλπ), είχε πολύ πιο γενικό νόημα στην αρχαία ελληνική, όπου σήμαινε τη δεξιότητα, ή τον τρόπο με τον οποίο κάτι μπορούσε να επιτευχθεί, ή ένα σύστημα ή μέθοδο για να φτιάξει κανείς κάτι (από εκεί έχουμε τη ρίζα των λέξεων “τεχνική”, “τεχνίτης”, “τεχνολογία”, κλπ). Ή ακόμη και η λέξη ποίηση, που αρχικά σήμαινε απλώς την κατασκευή, το φτιάξιμο (από το ρήμα ποιέω/ποιῶ). Κάτι ανάλογο θα μπορούσε να γίνει κάποτε και με τη λέξη “επιστήμη” στην ελληνική γλώσσα. Ας δούμε όμως τώρα συγκεκριμένα ποια είναι εκείνα τα ειδικά χαρακτηριστικά της επιστήμης (ως “science”), που δεν τα έχουν όλοι οι τομείς της γνώσης.
Η επιστημονική μέθοδος
Υπάρχει ένας κύκλος ο οποίος ακολουθείται προκειμένου η αποκτούμενη ανθρώπινη γνώση να γίνει μέρος της επιστημονικής γνώσης. Ο κύκλος αυτός περιλαμβάνει τα παρακάτω στάδια:
-
παρατήρηση
-
αρχική θεωρία
-
πείραμα – συλλογή δεδομένων
-
διαμορφωμένη θεωρία
-
δημοσίευση
-
κριτική
Υπόψη οτι δεν είναι όλα τα στάδια του κύκλου υποχρεωτικά. Επίσης, ο κύκλος συνεχίζεται συνήθως ανακυκλούμενος από το σημείο του πειράματος και κάτω. Ας δούμε τώρα τα στάδια αναλυτικά.
Παρατήρηση
Η αρχική παρατήρηση (ή παρατηρήσεις), αναφέρεται σε κάποια ιδιότητα του φυσικού κόσμου που παρατηρεί είτε ένας άνθρωπος, είτε μια ομάδα ατόμων, και είτε κατά τύχη, είτε σαν μέρος μιας συνειδητής προσπάθειας να γίνουν παρατηρήσεις.
Παράδειγμα τυχαίας παρατήρησης, από έναν άνθρωπο:
Το Φεβρουάριο του 1896, ο Γάλλος επιστήμονας Henri Becquerel (Ανρί Μπεκερέλ) εξέταζε κομμάτια ουρανίου, τα οποία άφηνε για μια μέρα εκτεθειμένα στον ήλιο, οπότε όταν τα έβαζε μετά πάνω σε φωτογραφική πλάκα (εκείνης της εποχής), έπαιρνε το αποτύπωμα του πετρώματος πάνω στο φιλμ. Αυτό ο Becquerel το εξήγησε υποθέτοντας οτι η ενέργεια του ηλιακού φωτός μαζευόταν κατά τη διάρκεια της μέρας στο ουράνιο, οπότε μετά αποδιδόταν στο περιβάλλον, και αποτυπωνόταν στο φωτογραφικό φιλμ. Μια μέρα πήρε ένα καινούργιο κομμάτι ουρανίου, αλλά καθώς ήταν συννεφιά και δεν είχε ήλιο, το έβαλε μέσα στο συρτάρι, πάνω στη φωτογραφική πλάκα. Προς μεγάλη-του έκπληξη, όταν ξαναέβγαλε το πέτρωμα από το συρτάρι μετά από κανα-δυό μέρες, είδε οτι αυτό είχε αφήσει το αποτύπωμά του πάνω στην πλάκα, παρόλο που το κομμάτι του ουρανίου δεν είχε εκτεθεί στο ηλιακό φως. Ο Becquerel είχε ανακαλύψει τυχαία το φαινόμενο της ραδιενέργειας.
Παράδειγμα παρατήρησης που προκύπτει μετά από συνειδητή προσπάθεια για ανακάλυψη:
Κατά τα τέλη του 19ου αιώνα είχε γίνει αντιληπτό από τους αστρονόμους οτι υπήρχαν ανωμαλίες στα δεδομένα της κίνησης των πλανητών Ουρανού και Ποσειδώνα, οπότε υποψιάστηκαν οτι θα υπήρχε ένας επιπλέον πλανήτης πέραν του Ποσειδώνα, που ίσως ήταν υπεύθυνος για τις ανωμαλίες αυτές. Τις έρευνες ξεκίνησε και χρηματοδότησε ο Αμερικανός αστρονόμος Percival Lowell (Πέρσιβαλ Λόουελ). Κανένα αποτέλεσμα όμως δεν βρέθηκε μέχρι το θάνατό του (πέθανε το 1916). Μόνο στις 18 Φεβρουαρίου του 1930, ο επίσης Αμερικανός νεαρός αστρονόμος Clyde Tombaugh (Κλάιντ Τόμπο) παρατήρησε ένα αμυδρό αστεράκι που είχε αλλάξει θέση πάνω σε δύο διαδοχικές φωτογραφίες που είχαν παρθεί σε διάστημα δύο εβδομάδων. Το “αστεράκι” αυτό ήταν ο πλανήτης Πλούτωνας. (Τότε, και μέχρι το 2006, ο Πλούτωνας ήταν ο ένατος πλανήτης, αλλά μετά “υποβιβάστηκε” στην κατηγορία των “νάνων πλανητών”.)
Αυτό το είδος της συνειδητής προσπάθειας για παρατήρηση μπορεί κάποτε να καταλήξει και στη σχεδόν κωμική περίπτωση του “σωστό κατά λάθος”! Στην πραγματικότητα περίπου τέτοια είναι η περίπτωση της ανακάλυψης του Πλούτωνα, γιατί το μέγεθος και η τροχιά του Πλούτωνα δεν εξήγησε τις ανωμαλίες που είχαν παρατηρηθεί στις τροχιές του Ουρανού και του Ποσειδώνα. Τελικά αποδείχτηκε οτι οι ανωμαλίες οφείλονταν σε λάθη κατά τις παρατηρήσεις του 19ου αιώνα! Αν δεν είχαν γίνει τα λάθη εκείνα δεν θα είχε ξεκινήσει η έρευνα για τον ένατο πλανήτη. Πιο χαρακτηριστική όμως είναι η περίπτωση της πρώτης “επιβεβαίωσης” της γενικής σχετικότητας, που εκτίναξε το κύρος του Αϊνστάιν στα ύψη. Ενώ η γενική σχετικότητα είναι — απ’ όσο γνωρίζουμε σήμερα — σωστή (και ο Αϊνστάιν δίκαια αξίζει τη φήμη-του), εντούτοις η πρώτη επιβεβαίωση της θεωρίας έγινε με λάθος τρόπο. Συγκεκριμένα, το 1919 ο Sir Arthur Eddington (Σερ Άρθουρ Έντιγκτον) φωτογράφισε την έκλειψη του Ήλιου που έγινε το έτος εκείνο, και υπολόγισε το πόσο καμπυλώθηκε το φως ενός αστεριού που οπτικά ήταν κοντά στον Ήλιο. Ο Eddington βρήκε μια τιμή καμπύλωσης που συμφωνούσε με την πρόβλεψη της γενικής σχετικότητας. Αργότερα προτάθηκε οτι οι υπολογισμοί του Eddington περιείχαν λάθη, που αν δεν είχαν γίνει θα βρισκόταν μια τιμή καμπύλωσης που δεν θα ήταν αρκετή για να επιβεβαιώσει τη θεωρία (ούτε και να την απορρίψει). Εντούτοις τα λάθη έγιναν, και η θεωρία “επιβεβαιώθηκε” το 1919. Βέβαια αργότερα έγιναν (και γίνονται) πάμπολλες άλλες ακριβείς επιβεβαιώσεις της θεωρίας της σχετικότητας.
Βλέπουμε λοιπόν οτι για να γίνουν παρατηρήσεις μετά από συνειδητή προσπάθεια για ανακάλυψη πρέπει συνήθως να υπάρχει ήδη μια θεωρία η οποία να κάνει κάποιες προβλέψεις, θέματα που θα δούμε σε λίγο. Πιο εντυπωσιακές είναι οι παρατηρήσεις που γίνονται κατά τύχη και οδηγούν σε επιστημονική ανακάλυψη. Μάλιστα στα αγγλικά υπάρχει και μια λέξη που περιγράφει αυτή την κατάσταση: serendipity, που σημαίνει το να κάνει κανείς ανακαλύψεις κατά τύχη· στα ελληνικά δεν υπάρχει αντίστοιχη λέξη.
Θεωρία
Οι παρατηρήσεις δημιουργούν ένα σύνολο δεδομένων, και ο σκοπός του επιστήμονα είναι να δημιουργήσει μια θεωρία που να εξηγεί αυτά τα δεδομένα, και να προβλέπει καινούργια. Παραδείγματος χάρη, ας υποθέσουμε οτι βλέπουμε τους παρακάτω αριθμούς:
7, 14, 21, 28, 35, 42, ...
Το ερώτημα είναι: ποιος αριθμός ακολουθεί στη θέση που είναι οι τρεις τελείες;
Συνήθως δεν παίρνει περισσότερο από μερικά δευτερόλεπτα για να δούμε οτι η παραπάνω είναι η ακολουθία των πολλαπλάσιων του επτά, οπότε αφού 42 = 6 x 7, έπεται οτι ο επόμενος αριθμός πρέπει να είναι ο 49 = 7 x 7.
Το παραπάνω παράδειγμα αποτελεί μια υπεραπλουστευμένη αφαίρεση της διαδικασίας παραγωγής μιας θεωρίας από προηγούμενες παρατηρήσεις. Οι παρατηρήσεις, ή “δεδομένα”, είναι οι αριθμοί 7, 14, 21, 28, 35, και 42. Η “θεωρία” που δημιουργούμε από τους αριθμούς αυτούς είναι η πρόταση: «Αυτοί οι αριθμοί είναι τα πολλαπλάσια του 7.» Έχοντας τη θεωρία που εξηγεί τα δεδομένα, μπορούμε να απαντήσουμε στο ερώτημα: «Ποιος είναι ο επόμενος αριθμός;» Μπορούμε δηλαδή να κάνουμε μια πρόβλεψη. Και αυτό είναι ένα χαρακτηριστικό που ξεχωρίζει την επιστήμη από την υπόλοιπη γνώση: μέσω της επιστήμης μπορούμε να προβλέπουμε το μέλλον, τουλάχιστο με κάποιο βαθμό βεβαιότητας (που όμως ποτέ δεν είναι 100%, όπως θα δούμε παρακάτω).
Ας δούμε ένα περισσότερο οπτικό–γεωμετρικό παράδειγμα. Έστω οτι τα δεδομένα είναι οι αριθμοί: 2, 9, 14, 17, 18, 17, 14, 9, 2.
Οι αριθμοί αυτοί θα μπορούσαν να είναι οι θερμοκρασίες που κατέγραψε ένα θερμόμετρο κατά τη διάρκεια μιας ημέρας, σε τακτά διαστήματα — π.χ. ανά ώρα. Δεν έχει σημασία όμως τί αντιπροσωπεύουν ή πώς συνελέγησαν· το σημαντικό είναι οτι πιστεύουμε πως έχουν αρκετά υψηλό βαθμό βεβαιότητας ώστε να τους θεωρούμε δεδομένα. (Το πώς εκτιμώνται οι βαθμοί βεβαιότητας εξηγείται σε επόμενη ενότητα.) Αναζητούμε τώρα μια θεωρία που να εξηγεί τα δεδομένα. Παρατηρούμε οτι αν τοποθετήσουμε τους αριθμούς 2, 9, 14, 17, 18, 17, 14, 9, και 2 ανά τακτά διαστήματα ανάλογα με το μέγεθός τους, παίρνουμε το εξής σχεδιάγραμμα:
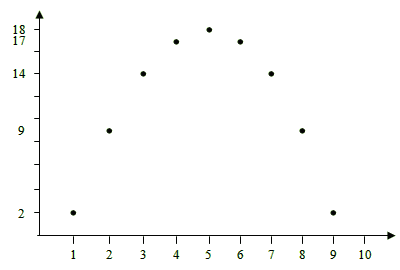
Η κάθε τελεία αντιστοιχεί σε ένα δεδομένο (αριθμό), κ’
έχει τοποθετηθεί
σε ύψος ανάλογο του μεγέθους-του: το πρώτο δεδομένο σε ύψος 2,
το δεύτερο δεδομένο σε ύψος 9, το τρίτο σε ύψος 14, κ.ο.κ.
Βλέπουμε οτι τα δεδομένα δεν είναι τυχαία, αλλά παρουσιάζουν ένα μοτίβο. Συγκεκριμένα, είναι σαν να ζωγραφίζουν μια καμπύλη. Αυτή η καμπύλη είναι η θεωρία που εξηγεί τα δεδομένα. Ας ενώσουμε τα δεδομένα με την καμπύλη που φαίνονται να σχηματίζουν:
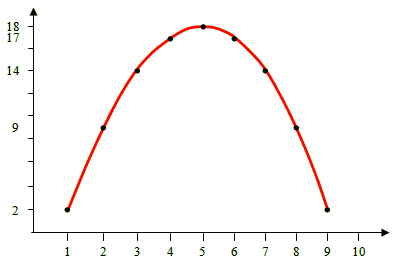
Στην κόκκινη καμπύλη, ή θεωρία, μπορούμε να δώσουμε και μαθηματική μορφή: πρόκειται για τη “συνάρτηση” y = 18 – (x – 5)2. Για κάθε τιμή του x (δηλ. x = 1, x = 2, x = 3, κλπ), παίρνουμε και ένα από τα δεδομένα-μας σαν τιμή του y (y = 2, y = 9, y = 14, κλπ).
Εφοδιασμένοι τώρα με τη θεωρία “y = 18
– (x – 5)2![]() ”,
μπορούμε να κάνουμε μία ή περισσότερες προβλέψεις: μπορούμε να
προβλέψουμε οτι ο 10ος αριθμός
θα πρέπει να είναι ο –7 (μείον επτά). Αυτό προκύπτει αν βάλουμε στη
θεωρία-μας την τιμή 10 στη θέση του x, οπότε για το y βγαίνει η τιμή –7.
Αν λοιπόν τα παραπάνω δεδομένα ήσαν θερμοκρασίες σε βαθμούς Κελσίου, η
θεωρία προβλέπει οτι την επόμενη ώρα η θερμοκρασία θα πέσει στους –7
βαθμούς (επτά υπό το μηδέν). Πάλι βλέπουμε λοιπόν οτι μια θεωρία κάνει
προβλέψεις που μπορεί να αποβούν χρήσιμες στην πράξη. («Αν η
θερμοκρασία πρόκειται να πέσει στους –7 βαθμούς, καλό είναι να εφοδιαστώ
με το βαρύ χειμωνιάτικο παλτό-μου», κλπ.)
”,
μπορούμε να κάνουμε μία ή περισσότερες προβλέψεις: μπορούμε να
προβλέψουμε οτι ο 10ος αριθμός
θα πρέπει να είναι ο –7 (μείον επτά). Αυτό προκύπτει αν βάλουμε στη
θεωρία-μας την τιμή 10 στη θέση του x, οπότε για το y βγαίνει η τιμή –7.
Αν λοιπόν τα παραπάνω δεδομένα ήσαν θερμοκρασίες σε βαθμούς Κελσίου, η
θεωρία προβλέπει οτι την επόμενη ώρα η θερμοκρασία θα πέσει στους –7
βαθμούς (επτά υπό το μηδέν). Πάλι βλέπουμε λοιπόν οτι μια θεωρία κάνει
προβλέψεις που μπορεί να αποβούν χρήσιμες στην πράξη. («Αν η
θερμοκρασία πρόκειται να πέσει στους –7 βαθμούς, καλό είναι να εφοδιαστώ
με το βαρύ χειμωνιάτικο παλτό-μου», κλπ.)
Επίσης, η ανακάλυψη της θεωρίας “y =
18 – (x – 5)2![]() ”
μας δίνει την αίσθηση της ικανοποίησης του οτι τώρα “καταλάβαμε” κάπως
καλύτερα τί είναι αυτοί οι αριθμοί, αφού έχουμε μια συνόψισή τους μέσω
της θεωρίας “y = 18 – (x – 5)2
”
μας δίνει την αίσθηση της ικανοποίησης του οτι τώρα “καταλάβαμε” κάπως
καλύτερα τί είναι αυτοί οι αριθμοί, αφού έχουμε μια συνόψισή τους μέσω
της θεωρίας “y = 18 – (x – 5)2![]() ”.
Η θεωρία λέμε οτι αποτελεί συνόψιση γιατί μπορεί να μας παραγάγει
(προβλέψει) και άλλους αριθμούς, όσους θέλουμε: ενδιάμεσους,
μελλοντικούς, και προηγούμενους, που ποτέ δεν μετρήσαμε με το θερμόμετρό
μας.
”.
Η θεωρία λέμε οτι αποτελεί συνόψιση γιατί μπορεί να μας παραγάγει
(προβλέψει) και άλλους αριθμούς, όσους θέλουμε: ενδιάμεσους,
μελλοντικούς, και προηγούμενους, που ποτέ δεν μετρήσαμε με το θερμόμετρό
μας.
Για να πάμε σε ένα πραγματικό και όχι τεχνητό παράδειγμα, με θεωρία που βγαίνει από παρατηρήσεις και μας δίνει προβλέψεις, ας σκεφτούμε τις εκλείψεις του Ήλιου. Έχοντας στη διάθεσή μας ένα πλήθος από παρατηρήσεις των θέσεων του Ήλιου και της Σελήνης (και των άλλων πλανητών) στο νοητό ουράνιο θόλο, καταστρώνουμε μια θεωρία για το πώς κινούνται τα ουράνια σώματα συν τω χρόνω. Έτσι μπορούμε να προβλέψουμε ποια θα είναι η θέση-τους σε οποιαδήποτε μελλοντική χρονική στιγμή. Άρα μπορούμε να προβλέψουμε επίσης πότε ο δίσκος της Σελήνης θα έρθει να καλύψει ένα μέρος από (ή και ολόκληρο) το δίσκο του Ήλιου, και να προκαλέσει ηλιακή έκλειψη. Έτσι, γνωρίζουμε οτι η επόμενη καλύτερα-ορατή από την Ελλάδα έκλειψη του Ήλιου, σχεδόν ολική, θα συμβεί στις 2 Αυγούστου του 2027, με το μέγιστο σημείο-της γύρω στις 11:30 π.μ.

Ολική έκλειψη του Ήλιου
Ας σημειωθεί οτι εκλείψεις προέβλεπαν και οι αρχαίοι λαοί, παρόλο που είχαν λάθος θεωρία του Ηλιακού συστήματος. Δηλαδή θεωρούσαν οτι η Γη είναι στο κέντρο, και όλα τα άλλα ουράνια σώματα κινούνται γύρω-της. Η θεωρία αυτή, που λέγεται γεωκεντρική, είναι πιο πολύπλοκη από την ηλιοκεντρική (που έχει τον Ήλιο στο κέντρο), και κάνει τους υπολογισμούς πιο δύσκολους. Βέβαια αν το μόνο που μας ενδιαφέρει είναι η κίνηση των ουρανίων σωμάτων όπως τα βλέπουμε από εδώ, από τη Γη, τότε η γεωκεντρική θεωρία (ή “Πτολεμαϊκό μοντέλο”) δεν είναι “λάθος”, αλλά απλώς πιο πολύπλοκη. Αλλά αν μας ενδιαφέρουν τα ταξίδια στο διάστημα, τότε θα διαπιστώσουμε με πολύ οδυνηρό τρόπο οτι η γεωκεντρική θεωρία είναι λάθος όταν το διαστημόπλοιό μας παρασυρθεί από το βαρυτικό πεδίο της κινούμενης Γης και χαθεί στο διάστημα. Στην περίπτωση των διαστημικών ταξιδιών υπάρχουν κι άλλα δεδομένα (π.χ., θέση παρατηρητή στον τριδιάστατο χώρο) με τα οποία δεν ασχολείται η θεωρία που ονομάζουμε “γεωκεντρικό μοντέλο”. Το αν λοιπόν μια θεωρία είναι “καλή” ή όχι εξαρτάται από το πόσα δεδομένα εξηγεί.
Σε επόμενες ενότητες του παρόντος μαθήματος θα εξετάσουμε πιο διεξοδικά τις θεωρίες, αλλά και τη σχέση-τους με τα δεδομένα.
Πείραμα – συλλογή δεδομένων
Συχνά η αρχική θεωρία μπορεί να επιβεβαιωθεί ή να τροποποιηθεί μέσω πειραμάτων στο εργαστήριο (ή στη φύση, ανάλογα με την περίπτωση). Το πείραμα έχει την έννοια οτι κάποιοι παράγοντες (οι “παράμετροι”) διατηρούνται σταθεροί, ενώ κάποιοι άλλοι μεταβάλλονται από αυτόν που εκτελεί το πείραμα, ο οποίος μεταβάλλοντας τις παραμέτρους παρατηρεί την επίδρασή τους.
Ιδού ένα γνωστότατο παράδειγμα, και ίσως ένα από τα πρώτα, με τα οποία εμπεδώθηκε η ιδέα οτι για να εξετάσουμε επιστημονικά τον φυσικό κόσμο πρέπει να πειραματιστούμε μ’ αυτόν. Λέγεται συχνά οτι ο Γαλιλαίος (1564–1642) έριξε δυο μπάλες, μια βαριά (σιδερένια) και μια ελαφριά (ξύλινη), από την κορυφή του κεκλιμένου πύργου της Πίζας, για να αποδείξει οτι και οι δύο μπάλες θα έφταναν ταυτόχρονα στο έδαφος — αντίθετα με την επικρατούσα τότε άποψη του Αριστοτέλη που έλεγε οτι τα βαριά αντικείμενα πέφτουν γρηγορότερα από τα ελαφριά. Το οτι έκανε ο Γαλιλαίος τέτοιο πείραμα είναι μύθος. Άλλωστε και να το έκανε, λόγω της αντίστασης που προβάλλει ο αέρας, η βαριά μπάλα όντως θα έφτανε γρηγορότερα στο έδαφος από την ελαφριά. (Σκεφτείτε π.χ. την ακραία περίπτωση οπου η “ελαφριά μπάλα” είναι ένα κοινό μπαλλόνι.) Για να πετύχει το πείραμα πρέπει να γίνει σε κενό αέρος, πράγμα που γνώριζε ο Γαλιλαίος, γιαυτό και δεν έκανε τέτοιο πείραμα, αλλά μόνο διατύπωσε την άποψη οτι έτσι έπρεπε να συμβεί. Το έκανε όμως ο αστροναύτης David Scott της αποστολής Apollo 15 το 1971 στο Φεγγάρι, όταν έριξε ένα σφυρί και ένα φτερό
| Σημείωση: για ελληνικούς υπότιτλους, αφού ξεκινήσετε το βίντεο, πατήστε το κόκκινο πλήκτρο με την ένδειξη CC → |
|
Βίντεο από την αποστολή Απόλλων 15 στο Φεγγάρι.
Ο αστροναύτης
David Scott εκτελεί το πείραμα του
Γαλιλαίου.
Όπως διαπίστωσε τόσο ο ίδιος ο Scott, όσο και εκατομμύρια τηλεθεατές, χάρη στην έλλειψη αέρα τα δύο αντικείμενα χτύπησαν στο έδαφος της Σελήνης ταυτόχρονα. Βέβαια μια τέτοια “οπτική” επιβεβαίωση δεν είναι επιστημονικά σωστή — ο Scott έκανε το πείραμα στο Φεγγάρι τόσο για λόγους θεάματος, όσο και για να αποτίσει φόρο τιμής στη μνήμη του Γαλιλαίου. Στην επιστημονικά αποδεκτή-του έκδοση, το πείραμα αυτό γίνεται στο εργαστήριο, μέσα σε θάλαμο με κενό αέρος, με χρονόμετρα ακριβείας, κλπ.
Με το πείραμα μπορούμε, όπως ήδη ειπώθηκε, να διατηρήσουμε κάποιες παραμέτρους σταθερές, και να τροποποιήσουμε κάποιες άλλες. Π.χ. στο πείραμα με τα σώματα που αφήνονται να πέσουν, μπορούμε να διατηρήσουμε το ύψος σταθερό και να μεταβάλουμε το βάρος των αντικειμένων. Αφού διαπιστώσουμε οτι — σε κενό αέρος — φτάνουν πάντα την ίδια στιγμή στο έδαφος, μπορούμε να κρατήσουμε σταθερό το βάρος, αλλά να μεταβάλουμε το ύψος από το οποίο πέφτουν, αναρωτιόμενοι ποιο ρόλο ακριβώς παίζει το ύψος. Στη συνέχεια μπορούμε να διατηρήσουμε σταθερά ύψος και βάρος, και να μεταβάλουμε το σχήμα-τους· και ούτω καθεξής.
Σημαντικό είναι να σημειώσουμε οτι οι αρχαίοι Έλληνες συνήθως δεν έκαναν πειράματα, αλλά απλώς διατύπωναν θεωρίες, οι οποίες έτσι έμεναν αστήρικτες. Αυτή ήταν η ουσιαστική διαφορά-τους από την επιστήμη όπως αυτή αναδύθηκε μετά το Μεσαίωνα. Γιαυτό οι αρχαίοι Έλληνες που μελέτησαν τη φύση λέγονται “προεπιστήμονες” (ή “φυσικοί φιλόσοφοι”). Ο Αριστοτέλης για παράδειγμα διατύπωσε την άποψη οτι οι γυναίκες έχουν λιγότερα δόντια από τους άντρες. Θα αρκούσε μια απλή εξέταση των δοντιών μερικών γυναικών (αρχίζοντας π.χ. από τη σύζυγό του Πυθιάδα) ώστε να απορρίψει την ιδέα αυτή. Και όμως δεν το έκανε, γιατί η πειραματική εξέταση της φύσης δεν ήταν μέρος της σκέψης των Ελλήνων. Η εξέταση της φύσης ήταν η “καινοτόμος ιδέα” που εισήχθηκε στην Ευρώπη κατά την Αναγέννηση και οδήγησε στην ανάπτυξη της επιστήμης με την έννοια του science. Και το μη-πείραμα του Γαλιλαίου απέκτησε μυθική διάσταση γιαυτόν ακριβώς το λόγο: επειδή έγινε κατανοητό οτι με ένα πείραμα θα μπορούσε να διακρίνει κανείς μεταξύ μιας λανθασμένης και μιας σωστής θεωρίας.
Για παράδειγμα, το γεωκεντρικό μοντέλο που αναφέρθηκε στην προηγούμενη ενότητα, μπορεί να ελεγχθεί μέσω πειράματος. Το πείραμα είναι οτι φτιάχνουμε ένα διαστημόπλοιο, ταξιδεύουμε στο διάστημα, και διαπιστώνουμε άμεσα ποια θεωρία είναι σωστή: η γεωκεντρική ή η ηλιοκεντρική. Βέβαια ένα τέτοιο πείραμα πρέπει να περιμένει την ανάπτυξη της τεχνολογίας που θα κάνει δυνατά τα διαστημικά ταξίδια. Τέτοια τεχνολογία δεν υπήρχε την εποχή του αρχαίου Αρίσταρχου του Σάμιου, που πρότεινε το ηλιοκεντρικό μοντέλο αντί για το γεωκεντρικό, ούτε αργότερα κατά την εποχή του Κοπέρνικου, ο οποίος πρότεινε το ίδιο πράγμα. Εκείνες τις εποχές οι άνθρωποι έπρεπε να αρκεστούν στο πόσο “ελκυστική” τους φαινόταν η μια θεωρία ή η άλλη, πράγμα για το οποίο θα μιλήσουμε αργότερα. Υπάρχουν όμως και σήμερα θεωρίες για τις οποίες δεν διαθέτουμε την απαραίτητη τεχνολογία για τα πειράματα που είτε θα τις επιβεβαιώσουν, είτε θα τις απορρίψουν. Τέτοιο παράδειγμα είναι η λεγόμενη θεωρία των υπερχορδών, στην κβαντική φυσική, που εξηγεί τις ιδιότητες των υποατομικών σωματιδίων. Για να ελέγξουμε πειραματικά τη θεωρία αυτή χρειαζόμαστε ποσότητα ενέργειας τόσο μεγάλη που δεν διαθέτουμε με τη σημερινή τεχνολογία. Άρα η θεωρία των υπερχορδών παραμένει προς το παρόν πειραματικά ανεπιβεβαίωτη.
Τελική θεωρία – δημοσίευση – κριτική
Μετά από τα τυχόν πειράματα και τη συλλογή των δεδομένων, καταστρώνεται μια τελική θεωρία, που είτε αποτελεί βελτίωση της αρχικής, είτε δημιουργείται εκ του μηδενός. Το σημαντικό είναι οτι η τελική θεωρία πρέπει να εξηγεί όλα τα δεδομένα: καί τις αρχικές (και πιθανά τυχαίες) παρατηρήσεις, καί τα όσα παρατηρήθηκαν μέσω πειραμάτων.
Απομένει πλέον η συγγραφή ενός άρθρου προς δημοσίευση (paper), που περιγράφει τα δεδομένα και τη θεωρία που τα εξηγεί. Αυτό στέλνεται προς δημοσίευση σε περιοδικά με κατάλληλο περιεχόμενο, ή προς αναγγελία σε συνέδρια που γίνονται πάνω σε σχετικό αντικείμενο, και είτε γίνεται αποδεκτό από τους εκδότες του περιοδικού (ή τους διοργανωτές του συνεδρίου), ή απορρίπτεται. Στην πραγματικότητα δεν είναι οι εκδότες ή διοργανωτές που αποφασίζουν, αλλά άλλοι συν-επιστήμονες, που διαβάζουν το άρθρο, και ο καθένας-τους λέει τη γνώμη-του στον εκδότη για το αν το κείμενο που τους δόθηκε κρίνεται κατάλληλο για δημοσίευση ή όχι. Οι συν-επιστήμονες υποτίθεται οτι κρίνουν αμερόληπτα, και στα πιο σοβαρά περιοδικά δεν έχουν γνώση του ονόματος του συγγραφέα, γιατί δεν τους το αποκαλύπτει ο εκδότης. Έτσι, κρίνουν αυστηρά βάσει του περιεχομένου, και δεν επηρεάζονται από το κύρος ή την αυθεντία του συγγραφέα — που είναι κάτι που επίσης θα συζητήσουμε αργότερα. Επίσης, ούτε ο συγγραφέας έχει γνώση του ποιοι είναι αυτοί που κρίνουν το κείμενό του, οπότε η πρακτική αυτή λέγεται “διπλά τυφλή” (“double blind”). Αφού λάβει τη γνώμη των άλλων επιστημόνων, ο εκδότης (που συνήθως είναι κι αυτός επιστήμονας) παίρνει την τελική απόφαση για το αν το κείμενο θα δημοσιευτεί ή όχι. Σχεδόν πάντα, η απόφαση, όταν είναι θετική, δεν είναι οτι το κείμενο δημοσιεύεται ως έχει, αλλά οτι πρέπει να γίνουν αλλαγές σύμφωνα με τις υποδείξεις των συν-επιστημόνων. Ο επιστήμονας-συγγραφέας κάνει τις αλλαγές μέσα στο προτεινόμενο χρονικό περιθώριο, και ξαναστέλνει το κείμενο. Αν το κείμενο λάβει την τελική έγκριση, τότε εμφανίζεται τυπωμένο σε κάποιο τεύχος του περιοδικού (ή στα πρακτικά του συνεδρίου, όταν γίνει αυτό).
Από κει και πέρα, όταν το κείμενο έχει δημοσιευτεί, υφίσταται την κριτική της ευρύτερης επιστημονικής κοινότητας, εφόσον μπορούν πλέον να το διαβάσουν όλοι. Η κριτική — που γίνεται πάλι μέσω δημοσιεύσεων — για να είναι επιστημονική, δεν μπορεί να βασίζεται στην υποκειμενική κρίση κανενός, αλλά στη συλλογή νέων δεδομένων από παρατηρήσεις. Δηλαδή, εφόσον μια θεωρία κάνει προβλέψεις, μπορεί κανείς να την ελέγξει πειραματικά και να δει αν τα νέα πειραματικά δεδομένα συμφωνούν με τις προβλέψεις. Εφόσον συμφωνούν, η θεωρία επιβεβαιώνεται. Εφόσον διαφωνούν, η θεωρία καθίσταται επισφαλής, και συνήθως απορρίπτεται. Έτσι δημιουργείται ένας κύκλος με νέα δεδομένα, νέα (βελτιωμένη) θεωρία, νέα δημοσίευση, κλπ. Βέβαια υπάρχει πάντοτε το ερώτημα για το κατά πόσο έγιναν σωστά τα νέα πειράματα, γιαυτό η θεωρία δεν απορρίπτεται αλόγιστα με την πρώτη δημοσίευση πειραματικών δεδομένων που αποφαίνεται οτι είναι λάθος. Όσο όμως εξακολουθούν να γίνονται παρατηρήσεις που αντίκεινται στις προβλέψεις της θεωρίας, τόσο αυξάνει η βεβαιότητα των επιστημόνων οτι η θεωρία είναι λανθασμένη.
Για το ερώτημα του ποιος είναι αυτός που αποδέχεται ή απορρίπτει μια θεωρία, η απάντηση είναι πως δεν πρόκειται για έναν συγκεκριμένο άνθρωπο, αλλά για ολόκληρη την επιστημονική κοινότητα. Η αποδοχή ή απόρριψη είναι πάντα έμμεση: αν οι άλλοι επιστήμονες κάνουν θετική αναφορά στη δημοσίευση με τη θεωρία αυτή, σημαίνει οτι την αποδέχονται σαν σωστή. Αν κάνουν αρνητική αναφορά, ή — πιο συχνά — όταν δεν αναφέρονται σ’ αυτήν καθόλου, η θεωρία δεν γίνεται αποδεκτή. Φυσικά όλη αυτή η διαδικασία περιλαμβάνει έναν υποκειμενικό παράγοντα: την κρίση των άλλων επιστημόνων. Επειδή όμως οι άλλοι επιστήμονες είναι πολλοί σε αριθμό, βάσει των νόμων της στατιστικής, η υποκειμενικότητα του ενός και η τυχόν προκατειλημένη κρίση-του δεν έχει αποτέλεσμα, γιατί χάνεται μέσα στο πλήθος της κρίσης των πολλών. Υποτίθεται οτι οι επιστήμονες σαν σύνολο δεν κρίνουν υποκειμενικά, γιατί έχουν γνώση της επιστημονικής μεθόδου και των αρχών που εξηγούνται στο παρόν μάθημα. Κρίνουν δηλαδή βάσει δεδομένων, και όχι βάσει της προκατειλημένης άποψης ή της φαντασίας-τους.
| Με βάση τα παραπάνω, ο αναγνώστης μπορεί εύκολα να απαντήσει (σαν άσκηση) το ακόλουθο ερώτημα: κατά πόσο είναι επιστήμονας ο δικηγόρος; Κατά πόσο ακολουθεί την επιστημονική μέθοδο; Πόσα από αυτά με τα οποία ασχολείται σχετίζονται με τα όσα αναφέρθηκαν μέχρι τώρα; |
Κριτική της επιστημονικής μεθόδου
Ο αναγνώστης θα σημείωσε ασφαλώς αρκετά σημεία, στα όσα αναφέρθηκαν, όπου υπάρχει η λέξη “υποτίθεται”. Η παραπάνω περιγραφή της επιστημονικής μεθόδου είναι η ιδεατή. Στην πράξη πάντα υπάρχουν ατέλειες — άλλωστε, πώς θα ήταν δυνατό να είναι διαφορετικά; Οι επιστήμονες, σαν άνθρωποι που είναι, κάνουν τα ίδια λάθη που κάνουν όλοι οι άνθρωποι.
Η προκατάληψη του επιστήμονα που προτείνει
Ο επιστήμονας που διαμορφώνει μια θεωρία, “κανονικά” πρέπει να την κρίνει αμερόληπτα, βάσει των δεδομένων και μόνο. Στην πράξη όμως, συχνά ο επιστήμονας αισθάνεται οτι η θεωρία-του είναι το “πνευματικό-του τέκνο”, και όπως ο γονέας υπερασπίζεται την υγεία και την ευημερία των βιολογικών παιδιών-του, κάτι παρόμοιο κάνει και όποιος επιστήμονας υπερασπίζεται τη “θεωρία-του”, ιδίως όταν αρχίσουν να συσσωρεύονται δεδομένα από παρατηρήσεις που την καταρρίπτουν. Κοιτώντας όμως τη γενική εικόνα της επιστήμης, δεν έχει και πολλή σημασία το αν κάποιος επιστήμονας υπερασπίζεται το “μωρό-του” ενάντια στις ενδείξεις, γιατί αυτό που μετράει είναι η μέση άποψη όλης της επιστημονικής κοινότητας, η οποία είναι πολύ πιο αντικειμενική, γιατί δεν έχει συναισθηματικό δεσμό με τη θεωρία του ενός ανθρώπου. Ας δούμε τί έγραφε για το θέμα αυτό ο Γάλλος χημικός Αντουάν-Λωράν Λαβουαζιέ (Antoine-Laurent Lavoisier, 1743–1794), το 18ο αιώνα:
“Η φαντασία, που μας παρασύρει διαρκώς πέρα από την πραγματικότητα, μαζί με τη φιλαυτία και την αυτοπεποίθηση που τόσο καλά ξέρουν να μας κατευθύνουν, μας ωθούν σε συμπεράσματα που δεν συνάγονται άμεσα από τα γεγονότα, με αποτέλεσμα να προσπαθούμε κατά κάποιον τρόπο να ξεγελάσουμε τον εαυτό μας. Δεν είναι λοιπόν παράξενο που γενικά στις επιστήμες της φύσης διατυπώνονται συχνά υποθέσεις αντί για τεκμηριωμένα συμπεράσματα [...]” “Ο μόνος τρόπος για να αποφύγουμε τέτοια παραστρατήματα είναι να απαλείψουμε ή τουλάχιστον να απλοποιήσουμε όσο μπορούμε τον συλλογισμό που είναι υποκειμενικός και ο οποίος είναι από μόνος του ικανός να μας παραπλανήσει, να τον υποβάλλουμε συνεχώς στον έλεγχο του πειράματος, να μην κρατούμε παρά τα γεγονότα εκείνα που είναι δεδομένα της φύσης και τα οποία δεν μπορούν να μας εξαπατήσουν, να αναζητούμε την αλήθεια μόνο στη φυσική αλληλουχία των πειραμάτων και των παρατηρήσεων [...]” Antoine-Laurent Lavoisier, 1789: Πρόλογος από το “Στοιχειώδης πραγματεία χημείας” (Traité élémentaire de chimie). Απόσπασμα από το βιβλίο: “Η «εντολή» του Γαλιλαίου”, Edmund Blair Bolles· απόδοση στα ελληνικά: Διονύσης Γιαννίμπας· Πανεπιστημιακές Εκδόσεις Κρήτης, Ηράκλειο 2004. |
Περισσότερα θα δούμε επίσης στην ενότητα περί διαψευσιμότητας.
Και το αντίθετο μπορεί να συμβεί: ένας επιστήμονας μπορεί να καταφέρεται ενάντια σε μια θεωρία που εχουν αναπτύξει άλλοι, παρόλο που τα δεδομένα δείχνουν να υποστηρίζουν τη θεωρία εκείνη. Παράδειγμα η θεωρία της Μεγάλης Έκρηξης (“Big Bang”) σαν εξήγηση των αρχικών σταδίων της εξέλιξης του σύμπαντος, την οποία πολέμησε “με νύχια και με δόντια” ο διάσημος αστρονόμος Fred Hoyle μέχρι το θάνατό του, παρόλο που τα δεδομένα που συσσωρεύονταν υποστήριζαν τη θεωρία αυτή, που αποτελεί σήμερα ακρογωνιαίο λίθο σχεδόν κάθε μοντέρνας κοσμολογικής θεωρίας. (Μάλιστα, ήταν ο Hoyle που εισήγαγε τον όρο “Big Bang” — «το Μεγάλο Μπαμ» — εμφανώς υποτιμητικά, θέλοντας να καταφέρει ένα “χτύπημα κάτω απ’ τη ζώνη” στη θεωρία, αλλά τελικά ο υποτιμητικός-του όρος ήταν αυτός ακριβώς που επικράτησε.)
Η προκατάληψη των επιστημόνων που κρίνουν
Όταν ένα άρθρο δίνεται προς κρίση από άλλους συν-επιστήμονες προκειμένου αυτοί να αποφασίσουν αν είναι άξιο για δημοσίευση ή όχι, συμβαίνει μερικές φορές το άρθρο ν’ απορριφθεί όχι για αντικειμενικούς λόγους, αλλά γιατί διαφωνεί με την “καθεστηκυία τάξη των πραγμάτων” στο νου των επιστημόνων–κριτών. Δηλαδή οι κριτές έχουν ήδη μια προαποφασισμένη άποψη για το ποια θεωρία είναι σωστή, και αντί να κοιτάξουν αμερόληπτα τα δεδομένα και ν’ αφήσουν τη θεωρία να δημοσιευτεί προκειμένου να κριθεί από την ευρύτερη επιστημονική κοινότητα, δεν το κάνουν αυτό αλλά απορρίπτουν το άρθρο, που δεν δημοσιεύεται. Αυτή η περίπτωση είναι πιο σπάνια από την προηγούμενη, γιατί οι κριτές είναι συνήθως τρεις ή περισσότεροι· πάντως δεν είναι καθόλου ανήκουστη. Αρκετοί επιστήμονες παραπονούνται γι’ αυτό, άλλοτε δίκαια, και άλλοτε άδικα.
Λάθη κατά τη συλλογή δεδομένων
Υπάρχει φυσικά η περίπτωση τα δεδομένα από τις παρατηρήσεις να έχουν λάθη. Αυτό είναι κάτι που δεν προκαλεί ιδιαίτερο πρόβλημα, γιατί άλλοι επιστήμονες θα κάνουν άλλες παρατηρήσεις, που θα διορθώσουν τις αρχικές. Στην παλαιοντολογία συμβαίνει κάποιες φορές να γίνεται όχι πολύ ακριβής αρχική εκτίμηση της ηλικίας ενός απολιθώματος. Με την επανάληψη των μετρήσεων όμως, το λάθος τελικά διορθώνεται. Άλλο ένα παράδειγμα από την αστρονομία: είναι γνωστή η λανθασμένη ηλικία μερικών αστέρων που υπολογιζόταν μέχρι και τη δεκαετία του 1990, όταν τα άστρα αυτά έβγαιναν να έχουν ηλικία μεγαλύτερη από αυτή του σύμπαντος! Τελικά η μέθοδος υπολογισμού της ηλικίας βελτιώθηκε, και αποδείχθηκε το προφανές, οτι δηλαδή τα άστρα αυτά είναι νεότερα από το ίδιο το σύμπαν.
Πολύ χειρότερη από τις παρατηρήσεις με λάθη είναι η σκόπιμη νόθευση των δεδομένων, ώστε αυτά να υποστηρίζουν τη θεωρία που προτείνεται. Αυτό δεν συμβαίνει συχνά, γιατί όταν συμβαίνει έχει σαν αποτέλεσμα την απομάκρυνση του ψευτοεπιστήμονα από την επιστημονική κοινότητα. Ο επιστήμονας που νοθεύει δεδομένα είναι σαν τον αστυνομικό που “λαδώνεται” από τον κακοποιό, ή σαν το μοναχό που όταν είναι μόνος-του καταριέται το Θεό που πιστεύει· πρόκειται δηλαδή για πράξη που καταφέρεται εναντίον ενός θεμελίου της επιστήμης, που είναι το εξής:
|
Από τα
δεδομένα φτιάχνονται οι θεωρίες, |
Όπως και με τα λάθη που γίνονται μη σκόπιμα, έτσι και με τα νοθευμένα δεδομένα, αργά ή γρήγορα κάποιοι άλλοι επαναλαμβάνουν τη διαδικασία συλλογής δεδομένων και έρχονται αντιμέτωποι με τη νοθεία. Τελικά για στατιστικούς λόγους τα λανθασμένα δεδομένα (τα σκόπιμα ή μη) μπαίνουν στο περιθώριο και αντικαθίστανται από τα σωστά.
Λάθη κατά την κατάστρωση της θεωρίας
Τέλος είναι δυνατό να είναι σωστά τα δεδομένα, αντικειμενική και η αντίληψη του επιστήμονα, αλλά η θεωρία που θα προκύψει να μην είναι σωστή. Αργά ή γρήγορα όμως κάποιος άλλος θα ανακαλύψει το λάθος και θα διορθώσει τη θεωρία. Παράδειγμα, η θεωρία του “αιθέρα”, κατά τα τέλη του 19ου αιώνα. Τα δεδομένα έρχονταν σε αντίφαση με τη θεωρία αυτή, που προσπαθούσε να “σώσει” την κλασική φυσική του Νεύτωνα, όπου η τελευταία συγκρουόταν με τις παρατηρήσεις για ηλεκτρομαγνητικά φαινόμενα, και συγκεκριμένα για την ταχύτητα του φωτός στο κενό. Τελικά ήρθε ο Αϊνστάιν, και από το 1905 και μετά πρότεινε την ορθότερη θεωρία της σχετικότητας, που κατέρριψε τη θεωρία περί αιθέρα και διόρθωσε την κλασική φυσική του Νεύτωνα.
Παρά τα παραπάνω ελαττώματα της επιστημονικής μεθόδου, η επιστήμη εν γένει μπορούμε να πούμε οτι καταφέρνει και ξεπερνάει τα προβλήματά της μέχρι σήμερα, παράγοντας αποτελέσματα που είναι αντικειμενικά σωστά, και που έχουν συνήθως ωφέλημα αποτελέσματα στην ποιότητα της ζωής των ανθρώπων.
Δεδομένα – Γεγονότα
Ποιες είναι οι ιδιότητες της έννοιας “επιστημονικό δεδομένο”
Υπάρχουν δύο είδη δεδομένων: τα δεδομένα μέτρησης, και τα δεδομένα ύπαρξης. (Εναλλακτικά, μπορούμε να μιλάμε για γεγονότα μέτρησης, και γεγονότα ύπαρξης. Για τους σκοπούς του παρόντος κειμένου, η λέξη “δεδομένο” θα χρησιμοποιείται σαν συνώνυμο της λέξης “γεγονός”, παρόλο που σε ένα γενικότερο πλαίσιο συμφραζομένων οι δύο λέξεις δεν έχουν ταυτόσημο νόημα.)
![]() Δεδομένα μέτρησης
προκύπτουν όποτε είναι δυνατό να μετρήσουμε μια ποσότητα και να της
εκχωρήσουμε μια τιμή. Π.χ., μετράμε διάφορα μήκη και γωνίες πάνω στην
επιφάνεια της Γης (όπως έκανε ο
Ερατοσθένης στην αρχαιότητα) και από
αυτά υπολογίζουμε τον όγκο της Γης, που είναι μια ποσότητα που
εκφράζεται σε μονάδες (π.χ. κυβικά χιλιόμετρα).
Δεδομένα μέτρησης
προκύπτουν όποτε είναι δυνατό να μετρήσουμε μια ποσότητα και να της
εκχωρήσουμε μια τιμή. Π.χ., μετράμε διάφορα μήκη και γωνίες πάνω στην
επιφάνεια της Γης (όπως έκανε ο
Ερατοσθένης στην αρχαιότητα) και από
αυτά υπολογίζουμε τον όγκο της Γης, που είναι μια ποσότητα που
εκφράζεται σε μονάδες (π.χ. κυβικά χιλιόμετρα).
![]() Δεδομένα ύπαρξης
προκύπτουν όποτε κάνουμε παρατηρήσεις από τις οποίες προκύπτει σαν
συμπέρασμα οτι “υπάρχει το Χ”, όπου το Χ είναι συνήθως αντικείμενο,
ή μπορεί επίσης να είναι μια σχέση μεταξύ αντικειμένων, ή
ιδιότητα αντικειμένου, ή ακόμη και ιδιότητα σχέσης. Π.χ.,
χρησιμοποιούμε ένα τηλεσκόπιο και βλέπουμε οτι υπάρχουν δορυφόροι γύρω
από τον πλανήτη Δία (όπως έκανε ο
Γαλιλαίος στην αυγή της Αναγέννησης).
Οι δορυφόροι είναι αντικείμενα. Με την ίδια παρατήρηση θα δούμε
οτι οι δορυφόροι αυτοί περιφέρονται γύρω από το Δία, και η περιφορά είναι σχέση μεταξύ
αντικειμένων. Βλέπουμε επίσης οτι ο κάθε δορυφόρος έχει μια ορισμένη
λαμπρότητα, που είναι ιδιότητα αντικειμένου. Τέλος, με
επαναληπτικές μετρήσεις βρίσκουμε οτι η περιφορά διαρκεί ορισμένες
ημέρες, που είναι ιδιότητα της σχέσης. Οι ιδιότητες είναι όλες
μετρήσιμα δεδομένα, ενώ τα αντικείμενα και οι σχέσεις είναι αποκλειστικά
δεδομένα ύπαρξης.
Δεδομένα ύπαρξης
προκύπτουν όποτε κάνουμε παρατηρήσεις από τις οποίες προκύπτει σαν
συμπέρασμα οτι “υπάρχει το Χ”, όπου το Χ είναι συνήθως αντικείμενο,
ή μπορεί επίσης να είναι μια σχέση μεταξύ αντικειμένων, ή
ιδιότητα αντικειμένου, ή ακόμη και ιδιότητα σχέσης. Π.χ.,
χρησιμοποιούμε ένα τηλεσκόπιο και βλέπουμε οτι υπάρχουν δορυφόροι γύρω
από τον πλανήτη Δία (όπως έκανε ο
Γαλιλαίος στην αυγή της Αναγέννησης).
Οι δορυφόροι είναι αντικείμενα. Με την ίδια παρατήρηση θα δούμε
οτι οι δορυφόροι αυτοί περιφέρονται γύρω από το Δία, και η περιφορά είναι σχέση μεταξύ
αντικειμένων. Βλέπουμε επίσης οτι ο κάθε δορυφόρος έχει μια ορισμένη
λαμπρότητα, που είναι ιδιότητα αντικειμένου. Τέλος, με
επαναληπτικές μετρήσεις βρίσκουμε οτι η περιφορά διαρκεί ορισμένες
ημέρες, που είναι ιδιότητα της σχέσης. Οι ιδιότητες είναι όλες
μετρήσιμα δεδομένα, ενώ τα αντικείμενα και οι σχέσεις είναι αποκλειστικά
δεδομένα ύπαρξης.
Είναι λάθος να νομίζουμε οτι κάτι μπορεί να χαρακτηριστεί είτε σαν “γεγονός” (που μας δίνει δεδομένα), είτε σαν “όχι γεγονός” (π.χ. “μια θεωρία”), χρησιμοποιώντας λογική άσπρου–μαύρου. Υπάρχουν διαβαθμίσεις στο πόσο μπορεί να θεωρείται κάτι σαν δεδομένο. Μερικά παραδείγματα θα ξεκαθαρίσουν αμέσως την ιδέα αυτή.
![]() Ας
ξεκινήσουμε με ένα παράδειγμα που μοιάζει να μας δίνει αναμφισβήτητα
ένα “δεδομένο μέτρησης”:
έστω οτι μας ζητούν τη θερμοκρασία του νερού σε έναν κουβά γεμάτο με
νερό. Πολύ απλά λοιπόν, εισάγουμε ένα κοινό θερμόμετρο στο νερό, και
δεδομένου οτι το νερό δεν είναι τόσο καυτό που να ξεπερνά τη μέγιστη
ένδειξη του θερμομέτρου, απλά διαβάζουμε την ένδειξη. Έστω οτι λέει: 25
βαθμοί. Είναι αυτό ένα δεδομένο; Έχουμε δηλαδή τώρα σαν δεδομένο οτι το
νερό έχει θερμοκρασία 25°C;
Ας
ξεκινήσουμε με ένα παράδειγμα που μοιάζει να μας δίνει αναμφισβήτητα
ένα “δεδομένο μέτρησης”:
έστω οτι μας ζητούν τη θερμοκρασία του νερού σε έναν κουβά γεμάτο με
νερό. Πολύ απλά λοιπόν, εισάγουμε ένα κοινό θερμόμετρο στο νερό, και
δεδομένου οτι το νερό δεν είναι τόσο καυτό που να ξεπερνά τη μέγιστη
ένδειξη του θερμομέτρου, απλά διαβάζουμε την ένδειξη. Έστω οτι λέει: 25
βαθμοί. Είναι αυτό ένα δεδομένο; Έχουμε δηλαδή τώρα σαν δεδομένο οτι το
νερό έχει θερμοκρασία 25°C;

Καταρχήν, μπορεί το θερμόμετρό μας να είναι ελαττωματικό. Αυτό όμως μπορούμε να το αντιμετωπίσουμε: εξετάζουμε το όργανο πριν από το πείραμα, συγκρίνοντάς το με άλλα παρόμοια. Κάνουμε λοιπόν το πείραμα μόνο εφόσον βεβαιωθούμε οτι το θερμόμετρό μας δεν είναι εμφανώς ελαττωματικό αλλά συμπεριφέρεται σαν όλα τ’ άλλα.
Και πάλι όμως υπάρχει πρόβλημα, γιατί δεν είναι δυνατόν όλα τα θερμόμετρα να είναι πανομοιότυπα και να δίνουν ακριβώς τις ίδιες μετρήσεις. Αυτό συμβαίνει γιατί λόγω μικροσφαλμάτων και μικροδιαφορών στην κατασκευή-τους (που ίσως και να χρειαζόμαστε μεγεθυντικό φακό για να τις δούμε) θα παρουσιάζουν μερικές μικρές αποκλίσεις. Οπότε γιατί να εμπιστευτούμε το θερμόμετρο που διαλέξαμε ανάμεσα από τα πολλά παρόμοια, και όχι κάποιο άλλο; Επίσης, η θερμοκρασία είναι ελαφρά διαφορετική σε διαφορετικά σημεία του νερού, γιατί ο κουβάς θερμαίνεται ή ψυχραίνει ανομοιόμορφα σε κάθε πλευρά-του, παρουσιάζοντας μικρο-ρεύματα μέσα στο υγρό, που μεταφέρουν αυτές τις διαφορές θερμοκρασίας, με αποτέλεσμα να υπάρχει ανομοιομορφία εφόσον επιθυμούμε μια αρκούντως ακριβή μέτρηση.
Κι αυτό το πρόβλημα όμως λύνεται εύκολα: ας μη βάλουμε ένα, αλλά 10, ή 100 θερμόμετρα μέσα στο νερό του κουβά. Συλλέγουμε τις θερμοκρασίες που δείχνουν (25,1°C, 24,8°C, 25,2°C,... κλπ), δηλαδή παίρνουμε ένα στατιστικό δείγμα, και παίρνουμε έτσι όχι μία απλή τιμή, αλλά ένα στατιστικό μέσο όρο. Π.χ. ο μέσος όρος των θερμοκρασιών του δείγματος μπορεί να είναι 25,073°C. Μάλιστα, μέσω πολύ απλών μεθόδων στατιστικής, μπορούμε να πούμε οτι βάσει του δείγματος η θερμοκρασία του νερού είναι μεταξύ 24,7°C και 25,3°C με βεβαιότητα 95%. Αν θέλουμε να μεγαλώσουμε τη βεβαιότητα, θα μεγαλώσει αντίστοιχα και το εύρος των δυνατών τιμών. (Π.χ., με βεβαιότητα 99% ο μέσος όρος των θεμοκρασιών ίσως να βρίσκεται μεταξύ 24,6°C και 25,4°C, τιμές που πάλι μας δίνουν οι ίδιοι απλοί τύποι της στατιστικής.)
Έτσι, το δεδομένο που προκύπτει από μετρήσεις δεν πρέπει να είναι ένας “σκέτος” αριθμός, αλλά μια στατιστική περιγραφή, συνοδευόμενη από κάποιο βαθμό βεβαιότητας. Όπως συνάγεται από τα παραπάνω, ο βαθμός βεβαιότητας μιας μέτρησης δεν μπορεί ποτέ να είναι απόλυτος, δηλαδή 100%.
![]() Ας
προχωρήσουμε τώρα σε “δεδομένα ύπαρξης”, που θα μας απασχολήσουν λίγο περισσότερο. Ένα
απλούστατο παράδειγμα είναι το εξής: είναι δεδομένο (γεγονός) το οτι ο
Παρθενώνας
υπάρχει;
Ας
προχωρήσουμε τώρα σε “δεδομένα ύπαρξης”, που θα μας απασχολήσουν λίγο περισσότερο. Ένα
απλούστατο παράδειγμα είναι το εξής: είναι δεδομένο (γεγονός) το οτι ο
Παρθενώνας
υπάρχει;

Εφόσον ζούμε στην πόλη της Αθήνας, είναι πολύ απλό να εξακριβώσουμε με τα μάτια-μας την αλήθεια αυτού του γεγονότος, καθώς αρκεί μια σύντομη βόλτα στην πόλη. (Ο Παρθενώνας φαίνεται από πάμπολλα σημεία των Αθηνών γιατί έτσι είναι κατασκευασμένη η πόλη.) Αν δεν ζούμε στην Αθήνα, αρκεί ένα ταξίδι στην Αθήνα για να διαπιστώσουμε την ύπαρξη του αρχαίου μνημείου με τα μάτια-μας και να δεχτούμε σαν δεδομένο οτι “ο Παρθενώνας υπάρχει”· άρα οτι τα βιβλία που τον απεικονίζουν (οι ιστοσελίδες, οι εικόνες της τηλεόρασης, κλπ) δεν συνομωτούν ώστε να μας παρουσιάσουν σαν αληθινό κάτι το ανύπαρκτο. Το πόσους κόπους, θυσίες, και έξοδα θα υποστούμε εξαρτάται από το πού βρισκόμαστε στον πλανήτη και πόσο πολύ επιθυμούμε να επιβεβαιώσουμε το δεδομένο. Αν ζούμε στην Αυστραλία θα πρέπει να υποστούμε μεγάλες θυσίες (οικονομικές, κλπ). Πάντως σε κάθε περίπτωση είμαστε καταρχήν σε θέση να αποφασίσουμε για το δεδομένο αυτό με τα ίδια-μας τα μάτια.
Αξίζει να σημειώσουμε οτι όταν έχουμε ένα αντικείμενο μπροστά στα μάτια-μας και αναρωτιόμαστε για το αν υάρχει, η βεβαιότητα με την οποία απαντάμε “ναι” και πάλι δεν μπορεί να είναι ακριβώς 100%. Π.χ. υπάρχουν άνθρωποι που αισθάνονται την ύπαρξη υπερφυσικών οντοτήτων γύρω-τους. Βέβαια ο Παρθενώνας δεν είναι υπερφυσική οντότητα, αλλά εντελώς φυσική. Και πάλι όμως, υπάρχουν άνθρωποι που βλέπουν εντελώς φυσικά αντικείμενα γύρω-τους (βλ. μάθημα Ν4, και συγκεκριμένα το “σύνδρομο Σαρλ Μπονέ”), και οι άνθρωποι αυτοί είναι απόλυτα φυσιολογικοί. Θα μπορούσαμε να είμαστε ένας απ’ αυτούς. Γνωρίζουμε βέβαια οτι οι πιθανότητες είναι μάλλον συντριπτικά υπέρ του οτι δεν είμαστε, αλλά ποτέ δεν μπορεί να είναι κανείς απόλυτα σίγουρος. Οπότε η βεβαιότητα δεν πρέπει να είναι ακριβώς 100% ούτε και για αντικείμενα που βρίσκονται “μπροστά στη μύτη-μας”.
![]() Ας
κάνουμε τώρα λίγο πιο δύσκολη την ερώτηση ύπαρξης δεδομένου: ο πλανήτης
Ποσειδώνας υπάρχει;
Ας
κάνουμε τώρα λίγο πιο δύσκολη την ερώτηση ύπαρξης δεδομένου: ο πλανήτης
Ποσειδώνας υπάρχει;

Ποσειδώνας
Για να απαντήσουμε αυτό το ερώτημα δεν αρκεί μια βόλτα στην πόλη, ούτε ένα ταξίδι με αυτοκίνητο ή αεροπλάνο. Πρέπει να εφοδιαστούμε (1) με τεχνολογία (τηλεσκόπιο ή δυνατά κυάλια) και (2) με τεχνογνωσία, ώστε να ξέρουμε σε ποιο σημείο του ουρανού και ποια ώρα της νύχτας να ψάξουμε. Κι αυτό όμως το ερώτημα δεν είναι πέρα από τις δυνατότητες του μέσου ανθρώπου που θέλει να δει με τα μάτια-του τον Ποσειδώνα: ούτε το τηλεσκόπιο ή τα ισχυρά κυάλια κοστίζουν πολύ, ούτε η πληροφορία είναι δύσκολο να βρεθεί (π.χ. μέσω διαδικτύου). Ισχύουν λοιπόν κ’ εδώ περίπου τα όσα είπαμε για το παράδειγμα του Παρθενώνα.
![]() Από
τη στιγμή όμως που τίθεται θέμα τεχνολογίας προκειμένου να διαπιστώσουμε
την ύπαρξη αντικειμένου, γίνεται αντιληπτό οτι το ερώτημα μπορεί να
είναι τέτοιο που να ξεπερνάει την ικανότητα του μέσου ανθρώπου να το
διαπιστώσει με τα δικά-του μάτια, ακόμα κι αν αυτός είναι διατεθειμένος
να υποστεί θυσίες και να μπει σε έξοδα. Π.χ.: ο δορυφόρος
Σαώ του Ποσειδώνα, υπάρχει;
Από
τη στιγμή όμως που τίθεται θέμα τεχνολογίας προκειμένου να διαπιστώσουμε
την ύπαρξη αντικειμένου, γίνεται αντιληπτό οτι το ερώτημα μπορεί να
είναι τέτοιο που να ξεπερνάει την ικανότητα του μέσου ανθρώπου να το
διαπιστώσει με τα δικά-του μάτια, ακόμα κι αν αυτός είναι διατεθειμένος
να υποστεί θυσίες και να μπει σε έξοδα. Π.χ.: ο δορυφόρος
Σαώ του Ποσειδώνα, υπάρχει;
(Αναπαράσταση της Σαούς, όχι πραγματική εικόνα)
Ελάχιστοι μόνο άνθρωποι στον κόσμο μπορούν να δώσουν απάντηση στο ερώτημα αυτό χρησιμοποιώντας τα ίδια-τους τα μάτια, γιατί η Σαώ του Ποσειδώνα είναι ένας μικροσκοπικός δορυφόρος ενός ήδη πολύ μακρινού πλανήτη. Χρειάστηκε επίσκεψη του Voyager-2 στην περιοχή του Ποσειδώνα το 1989 για να ανακαλυφθούν έξι δορυφόροι-του (όχι ακόμη η Σαώ) πέρα από τους μέχρι τότε δύο γνωστούς, ενώ ο συγκεκριμένος δορυφόρος ανακαλύφθηκε το 2002 από μια ομάδα Αμερικανών αστρονόμων. Ο “κοινός θνητός” έχει ελάχιστες ελπίδες να δει ποτέ με τα μάτια-του τη μικροσκοπική Σαώ.
Επομένως υπάρχουν “δεδομένα” (αμέτρητα σε πλήθος μάλιστα) για τα οποία δεν μπορούμε να βασιστούμε στην προσωπική-μας παρατήρηση για το αν θα τα δεχτούμε ή όχι. Πρέπει να βασιστούμε σε παρατηρήσεις άλλων ανθρώπων, που έχουν τα τεχνικά μέσα. Για το λόγο αυτόν ο βαθμός βεβαιότητας για την ύπαρξη της Σαούς θα πρέπει να είναι μικρότερος εκείνου που έχουμε για την ύπαρξη του Παρθενώνα ή του Ποσειδώνα. Όμως τί είδους παρατηρήσεις μπορούμε να κάνουμε δεκτές; Όλες οι παρατηρήσεις “μετράνε” σαν επιστημονικές; Και ποιους μπορούμε άραγε να εμπιστευόμαστε για την αποδοχή δεδομένων από παρατηρήσεις που έκαναν εκείνοι; Πώς γνωρίζουμε οτι δεν προσπαθούν να μας παραπλανήσουν, ή οτι δεν πλανώνται οι ίδιοι στο κάτω-κάτω;
Κριτήρια αποδοχής παρατηρήσεων: ποιου είδους παρατηρήσεις παράγουν επιστημονικά δεδομένα
Εφόσον τα “δεδομένα” που προκύπτουν από παρατηρήσεις παίζουν θεμελιώδη ρόλο στην επιστημονική μέθοδο, λογικό είναι να απαιτούμε να γνωρίζουμε τί είδους παρατηρήσεις μας δίνουν επιστημονικά δεδομένα. Θεωρείστε τα ακόλουθα παραδείγματα σαν κίνητρα προς σκέψη:
-
Βρίσκομαι σ’ ένα σκοτεινό δάσος, απομονωμένος από όλους τους άλλους ανθρώπους, και ξαφνικά ακούω μια φωνή να μου ψιθυρίζει στ’ αυτί «Πρόσεχε!». Κοιτάω γύρω-μου και βεβαιώνομαι οτι δεν υπάρχει κανένας εκεί κοντά. Είναι παρατήρηση αυτή; Είναι δεδομένο το οτι κάποιος ψιθύρισε στ’ αυτί-μου;
-
Μια αρχαία επιγραφή ενός λαού που έχει εξαφανιστεί 1000 χρόνια πριν γράφει οτι όλα τα μέλη της φυλής (που συμπεραίνουμε οτι αριθμούσαν πάνω από 1000 άτομα) είδαν με τα μάτια-τους μια γιγάντια αράχνη να κατεβαίνει από τον ουρανό και να προσγειώνεται σε κοντινό λόφο. Πρόκειται για παρατήρηση;
-
Τα μέλη μιας μικρής θρησκευτικής κοινότητας που ζουν απομονωμένα σε κάποια έρημο ισχυρίζονται οτι ο ηγέτης-τους έχει επανειλημένα κάνει θαύματα, γιατρεύοντας αρρώστους και ακόμα και ανασταίνοντας νεκρούς. Αυτό είναι παρατήρηση;
-
Οι μοναχοί ενός μοναστηριού κάνουν παρόμοιους ισχυρισμούς περί γιατρειάς (αλλά όχι περί αναστάσεων) που αποδίδουν σε μια θαυματουργή εικόνα. Αυτή μήπως είναι δεδομένο ή παρατήρηση;
-
Τα μέλη μιας θρησκείας που αριθμεί πάνω από ένα δισεκατομμύριο πιστούς ισχυρίζονται οτι, σύμφωνα με το ιερό-τους βιβλίο, ο ιδρυτής της θρησκείας-τους περπάτησε πάνω στην επιφάνεια του νερού. Μέλη άλλης θρησκείας, επίσης με πάνω από ένα δισεκατομμύριο πιστούς, ισχυρίζονται οτι το ιερό βιβλίο-τους είναι ο κατευθείαν λόγος του Θεού, όπως δόθηκε στον ιδρυτή της θρησκείας-τους. Μπορούμε να ονομάσουμε αυτά τα γεγονότα “δεδομένα”;
-
Οι κάτοικοι μιας σημερινής πόλης, με πληθυσμό πάνω από 20.000, ισχυρίζονται οτι είδαν φωτιές να διασχίζουν τον ουρανό μια συγκεκριμένη ημέρα και ώρα. Αυτό μήπως;
Οι παράγραφοι που ακολουθούν θα μας βοηθήσουν ν’ απαντήσουμε αυτά τα ερωτήματα.
Σε κάθε παρατήρηση δίνουμε ένα
βαθμό βεβαιότητας, ανάλογα με το κατά πόσο πιστεύουμε οτι είναι
αληθινή ή λανθασμένη. Η παρατήρηση δηλαδή δεν παίρνει μόνο δύο τιμές,
σωστή ή λάθος, αλλά ένα βαθμό βεβαιότητας, βάσει τεσσάρων κριτηρίων που
περιγράφονται αμέσως παρακάτω: επαληθευσιμότητα, αντικειμενικότητα, ανεξαρτησία, και πολλαπλότητα. Ο βαθμός είναι η πιθανότητα του
να είναι σωστή η παρατήρηση, δηλ. να αποτελεί “δεδομένο”. Μπορεί να
είναι σχεδόν 0, αν είμαστε σχεδόν βέβαιοι πως η παρατήρηση είναι λάθος![]() ·
ή μπορεί να είναι σχεδόν 1, αν είμαστε σχεδόν βέβαιοι οτι είναι σωστή· ή
μπορεί να έχει οποιαδήποτε τιμή μεταξύ 0 και 1, αλλά μη
συμπεριλαμβανομένων των δύο αυτών τιμών. Όσο πιο κοντά στο 1 είναι ο
βαθμός βεβαιότητας για μια παρατήρηση, τόσο πιο άνετα μπορούμε να
ονομάσουμε την παρατήρηση αυτή δεδομένο. Επομένως δεν λέμε οτι
μια παρατήρηση ή είναι δεδομένο ή δεν είναι, αλλά οτι κάποιες
παρατηρήσεις αξίζουν να λαμβάνονται σαν δεδομένα πιο πολύ από κάποιες
άλλες. Ιδού τώρα τα κριτήρια βάσει των οποίων εκχωρούμε ένα βαθμό
βεβαιότητας σε κάθε παρατήρηση.
·
ή μπορεί να είναι σχεδόν 1, αν είμαστε σχεδόν βέβαιοι οτι είναι σωστή· ή
μπορεί να έχει οποιαδήποτε τιμή μεταξύ 0 και 1, αλλά μη
συμπεριλαμβανομένων των δύο αυτών τιμών. Όσο πιο κοντά στο 1 είναι ο
βαθμός βεβαιότητας για μια παρατήρηση, τόσο πιο άνετα μπορούμε να
ονομάσουμε την παρατήρηση αυτή δεδομένο. Επομένως δεν λέμε οτι
μια παρατήρηση ή είναι δεδομένο ή δεν είναι, αλλά οτι κάποιες
παρατηρήσεις αξίζουν να λαμβάνονται σαν δεδομένα πιο πολύ από κάποιες
άλλες. Ιδού τώρα τα κριτήρια βάσει των οποίων εκχωρούμε ένα βαθμό
βεβαιότητας σε κάθε παρατήρηση.
Επαληθευσιμότητα
Το ουσιαστικότερο ίσως γνώρισμα που πρέπει να έχει μια παρατήρηση για να χαρακτηριστεί σαν επιστημονική είναι οτι πρέπει να είναι επαληθεύσιμη. Δηλαδή πρέπει να μπορούν και άλλοι παρατηρητές να κάνουν την ίδια παρατήρηση αφού αυτή ανακοινωθεί οτι έγινε (ή και ταυτόχρονα, αν αυτή αφορά σε αναμενόμενο, παγκόσμια παρατηρήσιμο γεγονός, όπως ένα αστρονομικό φαινόμενο).
Αυτή η απαίτηση απορρίπτει αμέσως την περίπτωση του ψιθύρου στο δάσος. Κανείς άλλος δεν μπορεί να επιβεβαιώσει το συμβάν εκτός από τον ίδιο τον άνθρωπο που είχε την εμπειρία. Μάλιστα, ούτε καν ο ίδιος ο άνθρωπος μπορεί να την επαληθεύσει, γιατί δεν μπορεί να την επαναλάβει. Όσο λοιπόν βέβαιος και αν είναι ο ίδιος οτι άκουσε έναν ψίθυρο ή μια φωνή, η εμπειρία-του δεν είναι επαληθεύσιμη, άρα δεν είναι ούτε επιστημονική. Η βεβαιότητα του ίδιου του ατόμου δεν έχει καμιά σημασία, γιατί αν ο άνθρωπος αυτός μελετήσει π.χ. νοολογία, θα μάθει οτι ο εγκέφαλος έχει μια περιοχή μέσω της οποίας εκχωρεί στον ίδιο-μας τον εαυτό την εσωτερική φωνή που ακούμε όταν σκεφτόμαστε (ή και όταν διαβάζουμε)· γνωρίζουμε δηλαδή κανονικά οτι η φωνή αυτή είναι δικό-μας παράγωγο. Όταν όμως για διάφορους λόγους η περιοχή αυτή του εγκεφάλου “σβήσει” (δηλαδή δεν δουλέψει σωστά και σιγήσει), όπως συμβαίνει σε κάποιες σπάνιες περιπτώσεις, τότε νομίζουμε οτι τη φωνή αυτή την παρήγαγε το εξωτερικό περιβάλλον, και όχι ο εαυτός-μας. Το ίδιο ακριβώς ισχύει και για οπτικές πληροφορίες: μπορεί κάποιος να δει ένα αντικείμενο, μια φιγούρα, μια “οντότητα” που να μοιάζει απόλυτα πραγματική σ’ αυτόν που νομίζει οτι τη βλέπει, και όμως αυτό να είναι προϊόν του εγκεφάλου κάτω από ιδιαίτερες συνθήκες λειτουργίας (π.χ.: κούραση, άγχος, στρες, πείνα), όταν “σιγήσει” ένα εγκεφαλικό κέντρο που μας επιτρέπει να καταλαβαίνουμε πότε αυτό που βλέπουμε είναι αληθινό, και πότε προϊόν της φαντασίας-μας. (Τα θέματα αυτά εξετάζονται αρκετά διεξοδικά στο μάθημα Ν4.) Εν πάση περιπτώσει, αυτή είναι μια εξήγηση του φαινομένου· ανεξάρτητα από την εξήγηση αυτή, η παρατήρηση είναι μη επιστημονική ως μη επαληθεύσιμη.
Η απαίτηση του να μπορεί να γίνει επαλήθευση της παρατήρησης μπορεί να δώσει την εντύπωση οτι ένα σωρό γεγονότα που συνέβησαν στο παρελθόν και που δεν μπορούν να συμβούν στο μέλλον είναι μη επιστημονικά ως μη επαληθεύσιμα. Για παράδειγμα, είναι η γνώση-μας περί των απολιθωμάτων μη επιστημονική, αφού κάθε απολίθωμα έγινε μια φορά στο παρελθόν, και εξ ορισμού δεν μπορεί να ξαναγίνει; Η απάντηση είναι οτι αν ενδιαφερόμαστε π.χ. για την ηλικία του απολιθώματος, όποιος επιστήμονας θέλει (και γνωρίζει πώς να το κάνει), μπορεί να υπολογίσει την ηλικία όσες φορές το επιθυμεί. (Στο μάθημα Β1 μαθαίνουμε πώς βρίσκονται οι ηλικίες των απολιθωμάτων.) Άρα το δεδομένο στην προκειμένη περίπτωση δεν είναι “το απολίθωμα” αλλά μια πέτρα με συγκεκριμένο σχήμα, χρώμα, βάρος, κλπ., και συγκεκριμένη ηλικία. Αυτά ασφαλώς και είναι επιστημονικά δεδομένα, καθώς είναι όλα επαληθεύσιμα. Αυτό το οποίο δεν είναι επαληθεύσιμο είναι η εξέλιξη του είδους Α στο είδος Β. Άρα η βιολογική εξέλιξη ενός είδους σε άλλο δεν αποτελεί δεδομένο (εκτός αν πρόκειται για εξέλιξη βακτηρίων ή ιών, που μπορεί να παρατηρηθεί στο εργαστήριο), αλλά θεωρία που εξηγεί τα δεδομένα (π.χ. των απολιθωμάτων, ή των διαφορών στο DNA). Αυτό που εννοούν κάποιοι επιστήμονες όταν λένε οτι «η εξέλιξη είναι γεγονός» είναι πως, δεδομένων των συντριπτικών ενδείξεων που είναι διαθέσιμες στον καθέναν που μελετά βιολογία, ο βαθμός βεβαιότητας για το οτι η θεωρία της εξέλιξης είναι σωστή είναι τόσο μεγάλος που η έννοια της εξέλιξης τοποθετείται μάλλον προς τη μεριά των “γεγονότων” στο φάσμα γεγονότα–θεωρίες, παρά προς τη μεριά των θεωριών. Αυτή η ιδέα θα γίνει ξεκάθαρη όταν ασχοληθούμε πιο διεξοδικά με τις θεωρίες, σε λίγο.
Τί θα μπορούσαμε να πούμε για τα ιστορικά γεγονότα, όπως το Ολοκαύτωμα κατά τον 2ο Παγκόσμιο Πόλεμο; Παίρνοντας υπόψη όλους τους παράγοντες που περιγράφονται στην ενότητα αυτή (και όχι μόνο την επαληθευσιμότητα) μπορούμε να αποκτήσουμε ένα βαθμό βεβαιότητας για ιστορικά γεγονότα. Για τη βεβαιότητα λαμβάνονται υπόψη παράγοντες όπως η πολλαπλότητα των πηγών, το πόσο μπορούμε να τις εμπιστευτούμε, κλπ (βλ. παρακάτω). Το Ολοκαύτωμα συγκεκριμένα, έχει καταγραφεί από τέτοιες πηγές και τόσο αντικειμενικά, ώστε μπορούμε να είμαστε σχεδόν απόλυτα βέβαιοι οτι συνέβη (ίσως τόσο βέβαιοι όσο και οτι ο 2ος Παγκόσμιος Πόλεμος συνέβη). Άλλα ιστορικά γεγονότα όμως, όπως π.χ. η “γενοκτονία των Αρμενίων” (του 1915), αμφισβητούνται από κάποιους (π.χ. Τούρκους) και υποστηρίζονται από άλλους (π.χ. Αρμένιους). Μπορούμε να έχουμε ένα βαθμό βεβαιότητας εξετάζοντας τις ιστορικές πηγές. Έτσι, η ιστορία είναι επιστημονικό πεδίο στο βαθμό που ασχολείται με την αντικειμενική περιγραφή των γεγονότων (βλ. αμέσως επόμενη υποενότητα), και παράγει θεωρίες που ερμηνεύουν τα γεγονότα και επιχειρούν να προβλέψουν το μέλλον.
Αντικειμενικότητα
Άλλη σημαντική απαίτηση είναι ο παρατηρητής να είναι αντικειμενικός. Για να καταλάβουμε γιατί, αρκεί να σκεφτούμε ένα πολύ γνωστό παράδειγμα: ας υποθέσουμε οτι ζητάμε από έναν πιστό της θρησκείας Χ να κρίνει αν η θρησκεία Ψ είναι ορθή ή όχι. Τότε, ανεξάρτητα από το αν η θρησκεία Χ είναι σωστή ή λάθος, ο πιστός της θρησκείας Χ θα απορρίψει τη θρησκεία Ψ, λέγοντας πως είναι λαθεμένη. (Αλλιώς ο πιστός της θρησκείας Χ θα έπρεπε να αλλάξει την πίστη-του και να πιστέψει στην Ψ.) Έτσι, αυτό το παράδειγμα δείχνει οτι, κατά βάθος, η έλλειψη αντικειμενικότητας σχετίζεται στενά με το πρόβλημα που εξετάσαμε πρωτύτερα, που είναι το να μπαίνουν οι γνώμες (θεωρίες) μπροστά από τις παρατηρήσεις και τα δεδομένα. Το να είναι κανείς αντικειμενικός σημαίνει να κοιτά τις ενδείξεις χωρίς προαποφασισμένες απόψεις, και να βγάζει συμπεράσματα μόνο από τις ενδείξεις, και όχι επειδή κάποια πράγματα θέλει να είναι αλήθεια.
Η αντικειμενικότητα είναι κι αυτή μια πολύ υψηλής σημασίας απαίτηση, όπως και η επαληθευσιμότητα. Χωρίς αντικειμενικότητα ουσιαστικά καταστρατηγείται ο σκοπός της παρατήρησης, που είναι να καταγράψουμε το τί συμβαίνει αντικειμενικά στον κόσμο, ανεξάρτητα από την προσωπική άποψη, ή τις προκαταλήψεις του παρατηρητή. Στην πράξη, ένας επιστήμονας μπορεί να είναι μη αντικειμενικός, ιδίως όταν αυτό το οποίο υποστηρίζει είναι προϊόν της δικής-του σκέψης. Όπως όμως ήδη αναφέρθηκε, το σύνολο των επιστημόνων πάσχει κατά πολύ λιγότερο από το πρόβλημα αυτό. Κατά συνέπεια, όταν έχουμε να κάνουμε με θεωρίες που κρίνονται σωστές από τη συντριπτική πλειοψηφία των επιστημόνων — όπως π.χ. η θεωρία της σχετικότητας, η θεωρία της εξέλιξης των ειδών, η θεωρία της κίνησης των τεκτονικών πλακών, κλπ. — τότε μπορούμε να είμαστε αρκετά βέβαιοι οτι η κρίση της επιστημονικής κοινότητας στο σύνολό της είναι αντικειμενική.
Μερικές φορές διατυπώνεται η
λανθασμένη άποψη — αποκλειστικά από άτομα που δεν συμμετέχουν στην
επιστημονική έρευνα και που αγνοούν την επιστημονική μέθοδο — οτι οι επιστήμονες σαν σύνολο είναι μη
αντικειμενικοί, οτι έχουν τάχα μια κρυφή ατζέντα, ή οτι βλέπουν τα
πράγματα από τη δική-τους, “επιστημονική σκοπιά”, που είναι μόνο μία από
τις διαθέσιμες προσεγγίσεις της πραγματικότητας. Πράγματι, η
επιστημονική είναι μόνο μία από τις διαθέσιμες προσεγγίσεις![]() ·
το θέμα όμως είναι οτι πρόκειται μάλλον για την κατά τεκμήριο
καλύτερη δυνατή, την πιο επιτυχημένη προσέγγιση, αν κρίνουμε
από την τεχνολογία — τον “καρπό” της επιστήμης — και τους χιλιάδες
τρόπους με τους οποίους η τεχνολογία βελτιώνει το βιοτικό επίπεδο των
ανθρώπων. Δεν είναι τυχαίο άλλωστε το οτι όταν επιζητείται επιβεβαίωση
κάποιας παρατήρησης ή ιδέας, αυτό που τονίζεται (όταν είναι δυνατό)
είναι οτι «είναι επιστημονικά αποδεδειγμένο...»· κανείς δεν
ισχυρίζεται οτι κάτι, π.χ., «είναι αστρολογικά αποδεδειγμένο».
·
το θέμα όμως είναι οτι πρόκειται μάλλον για την κατά τεκμήριο
καλύτερη δυνατή, την πιο επιτυχημένη προσέγγιση, αν κρίνουμε
από την τεχνολογία — τον “καρπό” της επιστήμης — και τους χιλιάδες
τρόπους με τους οποίους η τεχνολογία βελτιώνει το βιοτικό επίπεδο των
ανθρώπων. Δεν είναι τυχαίο άλλωστε το οτι όταν επιζητείται επιβεβαίωση
κάποιας παρατήρησης ή ιδέας, αυτό που τονίζεται (όταν είναι δυνατό)
είναι οτι «είναι επιστημονικά αποδεδειγμένο...»· κανείς δεν
ισχυρίζεται οτι κάτι, π.χ., «είναι αστρολογικά αποδεδειγμένο».
Ανεξαρτησία
Η βαρύτητα των παρατηρήσεων είναι μεγαλύτερη όταν οι παρατηρήσεις είναι ανεξάρτητες μεταξύ-τους.
Παράδειγμα: Σε μια περίπτωση, μια ομάδα τριών ανθρώπων ισχυρίζεται οτι καί οι τρεις είδαν έναν ιπτάμενο δίσκο να διασχίζει τον ουρανό, την ώρα που οι τρεις-τους είχαν ένα πικ-νικ στην εξοχή. Σε μια άλλη περίπτωση, τρεις άγνωστοι μεταξύ-τους άνθρωποι, από τρία διαφορετικά σημεία ενός τόπου, ισχυρίζονται οτι είδαν το ίδιο φαινόμενο: έναν ιπτάμενο δίσκο να διασχίζει τον ουρανό. Στη δεύτερη περίπτωση η παρατήρηση έχει μεγαλύτερη βαρύτητα, εφόσον διαπιστωθεί η ανεξαρτησία των παρατηρητών. (Π.χ. πρέπει να εξακριβωθεί το οτι οι τρεις-τους όντως δεν γνωρίζονταν και δεν ήσαν συνεννοημένοι.)
Πάντως, στο προηγούμενο παράδειγμα, σε καμία από τις δυο περιπτώσεις δεν έχουμε επιστημονική παρατήρηση, γιατί το γεγονός δεν είναι επαληθεύσιμο· εκτός εάν πάρθηκαν φωτογραφίες ή βίντεο του γεγονότος, οπότε τίθεται θέμα εξέτασης της γνησιότητας του υλικού, κλπ.
Παράδειγμα ανεξαρτησίας παρατηρήσεων από την επιστημονική πραγματικότητα: υπάρχουν δύο τρόποι για να συνάγουμε το πότε έζησε ο πιο πρόσφατος κοινός πρόγονος όλων των ανθρώπων που βρίσκονται σήμερα εν ζωή. Ένας τρόπος είναι εξετάζοντας την ηλικία των απολιθωμάτων που έχουν τα ίδια ανατομικά χαρακτηριστικά με τα δικά-μας, δηλαδή του είδους στο οποίο ανήκουμε: τον Άνθρωπο τον σοφό (Homo sapiens). Η ηλικία αυτή υπολογίζεται με διάφορες μεθόδους κβαντικής φυσικής (μέτρηση εναπομείνασας ποσότητας ισοτόπων κάποιων ατόμων), και βρίσκεται οτι είναι μεταξύ 150.000 και 200.000 χρόνια. Πρόσφατα (τις τελευταίες λίγες δεκαετίες) έχει αναπτυχθεί και μια δεύτερη μέθοδος: το “μοριακό ρολόι”. Αυτό αφορά σε εξέταση του DNA ενός αντιπροσωπευτικού δείγματος ανθρώπων που είναι εν ζωή σήμερα, και στη συνέχεια “πηγαίνοντας πίσω στο χρόνο”, χρησιμοποιώντας το ρυθμό με τον οποίο εμφανίζονται μεταλλάξεις στο DNA, και βρίσκοντας το πότε όλα τα μόρια DNA του δείγματος θα γίνονταν σχεδόν ίδια, συγκλίνοντας στο DNA του κοινού προγόνου όλων των μελών του δείγματος. Κι αυτή η μέθοδος μας δίνει μια παρόμοια ηλικία για τον πιο πρόσφατο κοινό-μας πρόγονο, πάλι μεταξύ 150.000 και 200.000 χρόνια. Επειδή οι δύο μέθοδοι είναι εντελώς ανεξάρτητες μεταξύ-τους, κ’ επειδή καταλήγουν στο ίδιο συμπέρασμα, έχουμε πολύ μεγαλύτερη βεβαιότητα για το συμπέρασμα απ’ ότι θα είχαμε αν ήμασταν γνώστες της μιας μόνο μεθόδου.
Πολλαπλότητα (ή πλήθος)
Το πλήθος των παρατηρήσεων παίζει κι αυτό ρόλο στο κατά πόσο μπορούμε να βασιστούμε σ’ αυτές. Στο παράδειγμα της θέασης του “ιπτάμενου δίσκου”, άλλη βαρύτητα έχει αν είδαν το φαινόμενο τρεις άνθρωποι (έστω και ανεξάρτητοι μεταξύ-τους), και άλλη αν το είδαν σχεδόν όλοι οι ενήλικοι μιας πόλης που αριθμεί 20.000 κατοίκους. Από μόνο-του όμως το μεγάλο πλήθος παρατηρητών δεν αρκεί για να θεωρηθεί σωστή μια παρατήρηση, καθώς υπάρχουν πασίγνωστα παραδείγματα περιπτώσεων όπου σχεδόν ολόκληρη η ανθρωπότητα πίστευε κάτι που φαινόταν σωστό επειδή αυτό έδειχνε η άμεση παρατήρηση, και όμως ήταν λάθος. Π.χ. κατά την αρχαιότητα σχεδόν όλοι πίστευαν οτι η Γη είναι επίπεδη, γιατί αυτό παρατηρούσαν με τα μάτια-τους. Επίσης έβλεπαν τα ουράνια σώματα να διαγράφουν τροχιές στον ουράνιο θόλο, και θεωρούσαν οτι η Γη είναι ακίνητη στο κέντρο του κόσμου, ενώ τα υπόλοιπα σώματα περιφέρονται γύρω-της· αλλά και ο “ουράνιος θόλος” καθαυτό είναι μια οφθαλμαπάτη. Επομένως, ναι μεν παίζει ρόλο το πλήθος των παρατηρήσεων/παρατηρητών, αλλά δεν μπορούμε να βασιστούμε αποκλειστικά σ’ αυτό (όσο μεγάλο κι αν είναι) για να πούμε οτι έχουμε ένα επιστημονικό δεδομένο.
Στο παράδειγμα του υπολογισμού της ηλικίας του πιο πρόσφατου κοινού-μας προγόνου, π.χ. μέσω DNA (“μοριακό ρολόι”), όσο πιο μεγάλο είναι το πλήθος των ατόμων του δείγματος (των οποίων εξετάζεται το DNA), τόσο πιο ασφαλές και ακριβές συμπέρασμα εξάγουμε για την υπολογιζόμενη ηλικία.
| Άσκηση: Με βάση τα παραπάνω, προσπαθήστε να απαντήσετε ένα-ένα τα παραδείγματα που αναφέρθηκαν στην αρχή αυτής της ενότητας. Η απαντήσεις-σας δεν πρέπει να καταλήγουν στο «ναί, είναι δεδομένο» ή «όχι, δεν είναι δεδομένο», αλλά στο με πόση βεβαιότητα (πάνω-κάτω) θα μπορούσατε να δεχτείτε τον ισχυρισμό σαν ορθό. |
Υποτιθέμενα “δεδομένα” που είναι στην πραγματικότητα θεωρίες
Στην επόμενη ενότητα θα εξετάσουμε προσεκτικά την έννοια της “θεωρίας”. Πρέπει όμως ήδη από το σημείο αυτό να πούμε οτι σε κάποια επιστημονικά πεδία γίνεται παραδεκτή η ύπαρξη ορισμένων “αντικειμένων” (ή και σχέσεις μεταξύ αντικειμένων), τα οποία ποτέ κανείς δεν έχει δει με τα μάτια-του, είτε γιατί δεν υπάρχει ακόμα η απαραίτητη τεχνολογία, είτε γιατί περιοριζόμαστε από τον τρόπο που λειτουργεί η ανθρώπινη όραση (οπότε δεν πρόκειται ποτέ να δούμε τα αντικείμενα αυτά, ανεξαρτήτως τεχνολογίας). Και όμως, δεχόμαστε οτι “υπάρχουν”, γιατί έτσι εξηγούνται ως ένα βαθμό (μερικές φορές πολύ μεγάλο) άλλες παρατηρήσεις που μπορούμε να κάνουμε επί άλλων αντικειμένων. Πρέπει να καταλάβουμε οτι τα “αντικείμενα” που δεν έχουν παρατηρηθεί απευθείας είναι στην πραγματικότητα θεωρίες, αλλά θεωρίες που κανείς επιστήμονας δεν μπορεί να απορρίψει· στο κάτω-κάτω δεν υπάρχει κάτι καλύτερο με το οποίο να μπορούν να αντικατασταθούν. Ας δούμε μερικά παραδείγματα.
![]() Υποατομικά σωματίδια:
Υποατομικά σωματίδια:
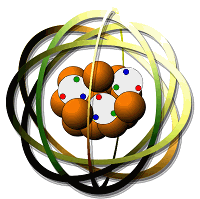

Σχηματικά μοντέλα ατόμου (αριστερά) και πρωτονίου
(δεξιά).
Μόνο σχηματικά μπορούν να παρασταθούν, με διαγράμματα που απέχουν πολύ
από την πραγματικότητα.
Κανείς δεν πρόκειται να δει ποτέ απευθείας ένα ηλεκτρόνιο, κουόρκ, γλουόνιο, νετρίνο, ή κάποιο άλλο από τα σωματίδια που αποτελούν την ύλη. Ο λόγος είναι οτι όταν βλέπουμε ένα αντικείμενο το βλέπουμε επειδή ένα ή περισσότερα φωτόνια εκπέμπονται από το αντικείμενο αυτό και συλλαμβάνονται από τον αμφιβληστροειδή χιτώνα του ματιού (όπου ενεργοποιούν ορισμένα φωτο-ευαίσθητα κύτταρα, τα “κωνία” και τα “ραβδία”). Όταν όμως το αντικείμενο που θέλουμε να δούμε είναι τόσο μικρό όσο ένα υποατομικό σωματίδιο, τότε το φωτόνιο είναι πολύ “χονδροειδές” σαν εργαλείο προκειμένου να δούμε το σωματίδιο. Όταν ένα ηλεκτρόνιο εκπέμπει ένα φωτόνιο, το ηλεκτρόνιο αλλάζει τις ιδιότητές του (π.χ. την ορμή-του, τη θέση-του στο χώρο), οπότε το φωτόνιο που συλλαμβάνει το μάτι-μας δεν μας δίνει ορθή πληροφορία για την τωρινή κατάσταση του ηλεκτρονίου. Με άλλα λόγια, η όραση (παρατήρηση μέσω φωτονίων) επηρεάζει το παρατηρούμενο αντικείμενο (το υποατομικό σωματίδιο). Για να μπορέσουμε να δούμε πραγματικά κάτι, πρέπει αυτό το κάτι να έχει αρκετά μεγάλη μάζα ώστε να μην επηρεάζεται σημαντικά από τα φωτόνια. Εφόσον λοιπόν βλέπουμε μόνο μέσω φωτονίων, δεν έχουμε καμιά ελπίδα να δούμε ποτέ ένα υποατομικό σωματίδιο· του οποίου η ύπαρξη επομένως μπορεί να συναχθεί μόνο έμμεσα: πρώτο επειδή εξηγεί ικανοποιητικά ένα πλήθος άλλων δεδομένων (μεταξύ των οποίων και το οτι λειτουργούν σωστά οι τηλεοράσεις, οι υπολογιστές, τα κινητά τηλέφωνα, τα GPS, και οποιοδήποτε άλλο προϊόν υψηλής τεχνολογίας), και δεύτερο επειδή προκύπτει σαν λύση εξισώσεων της κβαντικής φυσικής. Και τα επόμενα δύο παραδείγματα της γκρίζας ζώνης μεταξύ δεδομένων και θεωριών έχουν το χαρακτηριστικό αυτό: προκύπτουν σαν λύσεις εξισώσεων.
![]() Μαύρες τρύπες:
Μαύρες τρύπες:

Προσομοίωση εικόνας μαύρης τρύπας μέσω προγράμματος
υπολογιστή
Κανείς δεν έχει δει απευθείας μια μαύρη τρύπα στο διάστημα, γιατί, όντας μαύρη, θα μπορούσε να γίνει ορατή μόνο αν το υπόβαθρο ήταν κάποιο φωτεινό νεφέλωμα αντί για το (επίσης μαύρο) συνηθισμένο υπόβαθρο του διαστήματος. Επιπλέον όμως η μαύρη τρύπα έχει από τη φύση-της εξαιρετικά μικρές διαστάσεις στο χώρο· π.χ. διάμετρο μόλις μερικών χιλιομέτρων. Έτσι, δεν έχει παρατηρηθεί μέχρι σήμερα απευθείας μια μαύρη τρύπα. Ασφαλώς υπάρχουν άλλες παρατηρήσεις που συνηγορούν στην ύπαρξη μαύρης τρύπας, όπως ισχυρή εκπομπή ακτίνων Χ (λόγω της γειτονικής ύλης που “καταπίνεται” από τη μαύρη τρύπα, και που ακτινοβολεί ακτίνες Χ όταν πλησιάζει στον λεγόμενο “ορίζοντα γεγονότων” της τρύπας), ή περιφορά αστέρα γύρω από αόρατο αλλά με μεγάλη μάζα αντικείμενο — την υποτιθέμενη μαύρη τρύπα. Αυτά όμως είναι τα καθαυτό δεδομένα, που εξηγούνται καλύτερα από τη θεωρία οτι εκεί υπάρχει μια μαύρη τρύπα. Πρέπει να πούμε επίσης οτι οι μαύρες τρύπες δεν είναι αυθαίρετες επινοήσεις ευφάνταστων επιστημόνων, αλλά προκύπτουν σαν λύσεις εξισώσεων της θεωρίας της γενικής σχετικότητας.
![]() Βαρυτόνια: Τα βαρυτόνια, ή γκραβιτόνια (αγγλ.:
gravitons) είναι οι υποτιθέμενοι φορείς της βαρύτητας. Υποτίθεται
δηλαδή οτι δύο σώματα έλκονται βαρυτικά μεταξύ-τους επειδή ανταλλάσουν
βαρυτόνια. Κι αυτά προκύπτουν σαν λύσεις κβαντομηχανικών εξισώσεων αλλά η
ύπαρξή τους δεν έχει ανιχνευθεί ποτέ. Κι αυτό είναι αναμενόμενο, καθώς
για να έχουμε ελπίδες να ανιχνεύσουμε ένα βαρυτόνιο θα έπρεπε να έχουμε
μια ανιχνευτική συσκευή του μεγέθους του πλανήτη Δία (του μεγαλύτερου
πλανήτη του ηλιακού-μας συστήματος), να την τοποθετήσουμε σε στενή
τροχιά γύρω από έναν αστέρα νετρονίων (ένα σχετικά σπάνιο είδος αστέρα
που έχει εξαιρετικά μεγάλη πυκνότητα ύλης), και πάλι θα ελπίζαμε να
ανιχνεύσει η τερατώδης αυτή συσκευή μόνο ένα βαρυτόνιο κάθε δέκα χρόνια,
αν το ανίχνευε (πηγή).
Επειδή ένα τέτοιο σενάριο επιστημονικής φαντασίας είναι τεχνικά αδύνατο
να πραγματοποιηθεί, θα πρέπει να υποθέσουμε την ύπαρξη των βαρυτονίων
μόνο επειδή προκύπτουν σαν λύσεις εξισώσεων. Εδώ μάλιστα μπορούμε να
πούμε επιπλέον οτι δεν έχουμε ακόμη ούτε καν τα έμμεσα δεδομένα που θα
εξηγούνταν μέσω των βαρυτονίων (αν και γίνονται προσπάθειες με αυτόν
το στόχο). Άρα το “βαρυτόνιο” μοιάζει προς το παρόν περισσότερο με
θεωρία παρά με δεδομένο.
Βαρυτόνια: Τα βαρυτόνια, ή γκραβιτόνια (αγγλ.:
gravitons) είναι οι υποτιθέμενοι φορείς της βαρύτητας. Υποτίθεται
δηλαδή οτι δύο σώματα έλκονται βαρυτικά μεταξύ-τους επειδή ανταλλάσουν
βαρυτόνια. Κι αυτά προκύπτουν σαν λύσεις κβαντομηχανικών εξισώσεων αλλά η
ύπαρξή τους δεν έχει ανιχνευθεί ποτέ. Κι αυτό είναι αναμενόμενο, καθώς
για να έχουμε ελπίδες να ανιχνεύσουμε ένα βαρυτόνιο θα έπρεπε να έχουμε
μια ανιχνευτική συσκευή του μεγέθους του πλανήτη Δία (του μεγαλύτερου
πλανήτη του ηλιακού-μας συστήματος), να την τοποθετήσουμε σε στενή
τροχιά γύρω από έναν αστέρα νετρονίων (ένα σχετικά σπάνιο είδος αστέρα
που έχει εξαιρετικά μεγάλη πυκνότητα ύλης), και πάλι θα ελπίζαμε να
ανιχνεύσει η τερατώδης αυτή συσκευή μόνο ένα βαρυτόνιο κάθε δέκα χρόνια,
αν το ανίχνευε (πηγή).
Επειδή ένα τέτοιο σενάριο επιστημονικής φαντασίας είναι τεχνικά αδύνατο
να πραγματοποιηθεί, θα πρέπει να υποθέσουμε την ύπαρξη των βαρυτονίων
μόνο επειδή προκύπτουν σαν λύσεις εξισώσεων. Εδώ μάλιστα μπορούμε να
πούμε επιπλέον οτι δεν έχουμε ακόμη ούτε καν τα έμμεσα δεδομένα που θα
εξηγούνταν μέσω των βαρυτονίων (αν και γίνονται προσπάθειες με αυτόν
το στόχο). Άρα το “βαρυτόνιο” μοιάζει προς το παρόν περισσότερο με
θεωρία παρά με δεδομένο.
Τα παραπάνω παραδείγματα μας δείχνουν οτι δεν υπάρχει σαφής διαχωρισμός μεταξύ “δεδομένου” και “θεωρίας”. Υπάρχει μια “γκρίζα ζώνη” όπου οι δύο έννοιες συγχέονται. Στην πραγματικότητα υπάρχει ένα συνεχές φάσμα του οποίου το ένα άκρο ονομάζουμε “δεδομένα” και το άλλο άκρο “θεωρίες”. Για κάθε μέλος αυτού του φάσματος έχουμε απλώς ένα ποσοστό βεβαιότητας για το οτι “ισχύει”. Για κάποια μέλη (π.χ. “ύπαρξη Παρθενώνα”) έχουμε εξαιρετικά υψηλή βεβαιότητα, και δεν διστάζουμε να τα ονομάσουμε “δεδομένα”· για άλλα μέλη έχουμε μικρότερη βεβαιότητα, οπότε προτιμούμε να τα ονομάζουμε “θεωρίες”· δεν υπάρχει όμως κάτι που να διακρίνει ακριβώς το δεδομένο από τη θεωρία.
Ας δούμε όμως τώρα πιο προσεκτικά τί ιδιότητες απαιτούμε να έχουν αυτά που ονομάζουμε “επιστημονικές θεωρίες”.
Θεωρίες
Αν όλο κι όλο που μας ενδιέφερε ήταν η παρατήρηση και η συλλογή δεδομένων, η επιστήμη σήμερα θα ήταν ανύπαρκτη, και θα βρισκόμασταν ακόμα σε αρχαϊκό, προεπιστημονικό στάδιο. Για παράδειγμα, οι αριθμοί 7, 14, 21, 28, 35, και 42, από μόνοι-τους είναι άχρηστοι, δεν μας βοηθούν σε τίποτα. Το ζήτημα είναι να παρατηρήσουμε οτι «είναι τα πολλαπλάσια του 7», δηλαδή να διατυπώσουμε αυτή τη “θεωρία”, ή “υπόθεση”, ώστε να είμαστε σε θέση να προβλέψουμε ποιος αριθμός έπεται. Αυτός είναι και ένας από τους κύριους στόχους της επιστήμης: να προβλέπει το μέλλον. Όταν π.χ. ο μετεωρολόγος μας ανακοινώνει τί καιρό θα κάνει αύριο, δεν έχει αρκεστεί σε μια απλή καταγραφή των αριθμών που έστειλε ο δορυφόρος, αλλά έχει δώσει τους αριθμούς αυτούς σε κάποιο μετεωρολογικό μοντέλο (τη “θεωρία”), και από το μοντέλο αυτό προέκυψε μια πρόγνωση.
Πότε όμως λέμε οτι έχουμε μια επιστημονική θεωρία; Μπορεί π.χ. να ισχυριστεί κανείς οτι βάσει των παρατηρήσεών μας σχετικά με το πώς είναι οργανωμένος ο φυσικός κόσμος, έπεται οτι κάποια Υπέρτατη Δύναμη πρέπει να τον δημιούργησε. Είναι επιστημονικά αποδεκτή η θεωρία αυτή;
Διαψευσιμότητα
Η πιο σημαντική ιδιότητα που απαιτείται να έχει μια θεωρία για να μπορεί να χαρακτηριστεί “επιστημονική” είναι οτι πρέπει να είναι διαψεύσιμη.
Παράδειγμα: Αν, δοθέντων των αριθμών 7, 14, 21, 28, 35, και 42, διατυπώσουμε τη θεωρία οτι «είναι τα πολλαπλάσια του 7», και επομένως κάνουμε την πρόβλεψη οτι ο επόμενος αριθμός θα είναι ο 49, τότε έχουμε μια διαψεύσιμη, και άρα επιστημονική θεωρία. “Διαψεύσιμη” σημαίνει “ικανή να αποδειχτεί λανθασμένη”, εξαρτώμενη από τα δεδομένα που θα παρατηρηθούν στο μέλλον. Για παράδειγμα, αν ο επόμενος αριθμός τύχει να μην είναι ο 49, τότε η θεωρία-μας θα έχει διαψευστεί, και θα πρέπει να την αλλάξουμε ώστε η νέα θεωρία να περιλάβει τόσο τους παλιούς όσο και το νέο αριθμό, που είναι απροσδόκητος σύμφωνα με την παλιά θεωρία. Π.χ., αν ο επόμενος αριθμός τύχει να είναι ο 50, ιδού μια νέα, βελτιωμένη θεωρία: «Είναι τα πρώτα έξι πολλαπλάσια του 7· από κει και πέρα πρέπει να προσθέτουμε 1 σε κάθε επόμενο πολλαπλάσιο του 7.» (Υπόψη οτι φαίνεται πολύπλοκη η νέα θεωρία, αλλά ένας μαθηματικός μπορεί εύκολα να γράψει έναν τύπο που να συνοψίζει την παραπάνω πρόταση μέσα σε λίγες πράξεις.)
Τί γίνεται αν δεν πρόκειται να παραχθεί κανένα νέο δεδομένο (νέος αριθμός); Τότε η θεωρία-μας δεν μπορεί να διαψευστεί, γιατί ναι μεν κάνει μια πρόβλεψη (οτι ο επόμενος αριθμός θα είναι ο 49), αλλά αφού δεν πρόκειται να υπάρξει επόμενος αριθμός, κανείς δεν θα μπορέσει ποτέ να διαψεύσει τη θεωρία αυτή, δηλαδή να δει αν είναι σωστή ή όχι. Μπορεί π.χ. οι δοσμένοι αριθμοί (7, 14, 21, 28, 35, και 42) να παρήχθησαν από κάποια άλλη, πιο πολύπλοκη μέθοδο από τα πολλαπλάσια του 7, πράγμα που δεν θα το μάθουμε ποτέ αφού δεν θα παραχθεί κανένα νέο δεδομένο. Στην περίπτωση λοιπόν αυτή, εφόσον δεν μπορούμε να εξετάσουμε λεπτομερειακά τη μέθοδο μέσω της οποίας παρήχθησαν οι αριθμοί αυτοί, παύουμε να έχουμε μια θεωρία. Έχουμε να κάνουμε με ένα δεδομένο: τους έξι αυτούς αριθμούς και τίποτ’ άλλο. Εφόσον όμως μπορούμε να εξετάσουμε τη μέθοδο (π.χ. ένα πρόγραμμα υπολογιστή που υπολογίζει και παράγει αυτούς τους έξι αριθμούς, έναν-έναν), τότε και πάλι δεν έχουμε μια θεωρία, αλλά μια πλήρη κατανόηση του βαθύτερου μηχανισμού, του υπεύθυνου για την παραγωγή των δεδομένων αυτών.
Ας προχωρήσουμε σε πιο πραγματικά παραδείγματα. Έστω οτι παρατηρούμε τους κύκνους που υπάρχουν στον κόσμο. Βρισκόμαστε ακόμα στα 1600, όταν η Αμερική έχει ήδη ανακαλυφθεί, αλλά όχι ακόμα και η Αυστραλία. Όλοι οι κύκνοι που έχουν παρατηρηθεί σε όλα τα μέρη του κόσμου, περιλαμβανομένης και της Αμερικής, είναι λευκοί.
 |
 |
 |
 |
| Cygnus buccinator | Cygnus olor | Cygnus melanocorypha | Coscoroba coscoroba |
Παραδείγματα ειδών λευκών κύκνων, από Ευρώπη, Αμερική (Βόρεια και Νότια) και Ασία.
Διατυπώνουμε λοιπόν τη θεωρία οτι «οι κύκνοι είναι πάντοτε λευκοί», που συμφωνεί με όλα τα μέχρι στιγμής δεδομένα. Η θεωρία είναι διαψεύσιμη, γιατί αν βρεθεί ποτέ ένας μη λευκός κύκνος, θα έχει διαψευστεί. Πράγματι, μετά την ανακάλυψη της Αυστραλίας παρατηρούμε οτι υπάρχει το είδος του μαύρου κύκνου Cygnus atratus, οπότε η θεωρία-μας διαψεύδεται.

Το είδος του μαύρου κύκνου της Αυστραλίας, Cygnus atratus (βλ. πληροφορίες εδώ)
Σημαντικό είναι να ξεχωρίσουμε την έννοια “διαψεύσιμη” από την έννοια “σωστή/λάθος”. Μια θεωρία μπορεί να είναι σωστή, και να παραμένει διαψεύσιμη. (Πάντοτε πρέπει να παραμένει διαψεύσιμη για να είναι επιστημονική.) Για παράδειγμα, αν ακόμα και οι κύκνοι της Αυστραλίας ήσαν λευκοί, η θεωρία περί μόνο λευκών κύκνων θα ήταν σωστή, αλλά θα παρέμενε διαψεύσιμη, γιατί πάντα μπορεί να βρίσκαμε κάποιον μέχρι πρότινος ανεξιχνίαστο βιότοπο στη Γη με μη-λευκούς κύκνους. Τώρα, αν έχουμε ψάξει όλες τις “γωνιές” της Γης (και είμαστε απόλυτα βέβαιοι οτι δεν υπάρχει μέρος που δεν ψάξαμε), και δεν έχουμε βρει παρά μόνο λευκούς κύκνους, τότε πλέον δεν έχουμε μια θεωρία, αλλά ένα δεδομένο: «όλοι οι κύκνοι είναι λευκοί».
Όσο τα νέα δεδομένα που έρχονται εξακολουθούν να υποστηρίζουν τη θεωρία, δηλαδή να μην τη διαψεύδουν, τόσο μεγαλώνει η βεβαιότητά μας οτι η θεωρία είναι σωστή. Ποτέ όμως η βεβαιότητά μας δεν γίνεται ίση με 100%, εκτός αν γνωρίζουμε οτι τελείωσαν τα δεδομένα, όπως στο παραπάνω υποθετικό παράδειγμα με τους κύκνους.
Ας προχωρήσουμε την παραπάνω σκέψη, “τραβώντας-τη στα άκρα”. Γνωρίζουμε οτι όταν αφήνουμε ένα αντικείμενο ελεύθερο από κάποιο ύψος, αυτό πέφτει προς την επιφάνεια της Γης. Για το φαινόμενο αυτό έχουμε μια θεωρία: τη θεωρία της βαρύτητας, που ήταν μέρος της κλασικής φυσικής του Νεύτωνα, και τώρα μέρος της θεωρίας της σχετικότητας του Αϊνστάιν. Όσες φορές και να έχουμε αφήσει ένα αντικείμενο να πέσει, αυτό έχει κατευθυνθεί επιταχυνόμενο προς τα κάτω, πάντα επιβεβαιώνοντας τη φυσική θεωρία. Ποτέ δεν είδαμε ένα αντικείμενο να ανεβαίνει προς τα πάνω, ή να πηγαίνει προς άλλη διεύθυνση. (Αντικείμενο βαρύτερο του αέρα· ας αποκλείσουμε μπαλόνια ηλίου ή θερμού αέρα — που άλλωστε κι αυτά επιβεβαιώνουν τη θεωρία, αφού είναι ο βαρύτερος απ’ αυτά αέρας που “πέφτει” γύρω-τους.) Τί σημαίνει αυτό; Οτι η θεωρία της βαρύτητας έχει επιβεβαιωθεί πλήρως; Είναι διαψεύσιμη ή όχι;
Ασφαλώς και δεν έχει επιβεβαιωθεί 100% η θεωρία, και φυσικά είναι διαψεύσιμη. Η θεωρία προβλέπει οτι την επόμενη φορά που θ’ αφήσουμε ελεύθερο ένα αντικείμενο βαρύτερο του αέρα, θα πάει κι αυτό επιταχυνόμενο προς τα κάτω. Αν όμως δούμε ποτέ, έστω και μία φορά, να μη συμβαίνει αυτό — κ’ εφόσον βεβαιωθούμε οτι δεν έχουμε πέσει θύματα ταχυδακτυλουργίας, αυθυποβολής, κλπ. — η τρέχουσα θεωρία της βαρύτητας θα έχει διαψευστεί, και θα πρέπει να τη συμπληρώσουμε, ώστε η νέα θεωρία να περιλαμβάνει και το νέο δεδομένο. Φυσικά, αυτό το παράδειγμα είναι “των άκρων” γιατί τα φυσικά αντικείμενα πέφτουν εκατομμύρια φορές κάθε ημέρα σε όλη τη Γη, και ποτέ κανείς δεν παραπονέθηκε οτι κάποιο-τους έφυγε προς τα πάνω και χάθηκε στο διάστημα. Άρα έχουμε αντίστοιχη βεβαιότητα, που πλησιάζει το σχεδόν ακριβώς 100%. Δεν πρέπει όμως να είναι ποτέ ακριβώς 100%.
|
Άσκηση:
Ο αναγνώστης ας προσπαθήσει να φανταστεί ένα νέο νόμο
βαρύτητας, που να είναι συμβατός με όλες τις παρατηρήσεις
που έχουν γίνει μέχρι σήμερα· δηλαδή να εξηγεί γιατί όλα τα
αντικείμενα που παρατηρούμε καθημερινά κατευθύνονται προς το
κέντρο της Γης (ή του πλανήτη γενικότερα), αλλά ο νέος νόμος
να προβλέπει κάποιες καινούργιες παρατηρήσεις που, αν τις
κάναμε, θα διέψευδαν το σημερινά αποδεκτό νόμο της
βαρύτητας. Εννοείται οτι ο νέος νόμος πρέπει να είναι
συμβατός με τους άλλους φυσικούς νόμους, δηλαδή να μη
γίνεται επίκληση σε υπερφυσικές δυνάμεις. |
Ας πάμε στη θεωρία της εξέλιξης των ειδών. Θα μπορούσε να ισχυριστεί κανείς οτι η θεωρία αυτή αφορά σε πράγματα που συνέβησαν στο παρελθόν. Είναι μια θεωρία που αφορά αποκλειστικά στο παρελθόν, επομένως δεν κάνει προβλέψεις για το μέλλον που να μπορούν να ελεγχθούν, τουλάχιστον σε εύθετο χρόνο και όχι μετά από εκατομμύρια χρόνια· άρα δεν είναι διαψεύσιμη· άρα ούτε επιστημονική. Είναι σωστή αυτή σαν σκέψη;
Όχι, είναι λάθος. Η θεωρία της εξέλιξης των ειδών πράγματι κάνει ελεγχόμενες προβλέψεις. Για παράδειγμα, κάνει την πρόβλεψη οτι ποτέ δεν πρόκειται να βρούμε ένα απολίθωμα θηλαστικού με ηλικία μεγαλύτερη από 400 εκατομμύρια έτη (γιατί τόσο παλιά δεν είχαν εξελιχθεί ακόμα σε θηλαστικά τα ζώα)· ποτέ δεν πρόκειται να βρούμε απολίθωμα του δικού-μας είδους (Homo sapiens) με ηλικία μεγαλύτερη από 1 εκατομμύριο έτη· κ.ο.κ. Τη στιγμή που θα βρούμε ένα απολίθωμα με ηλικία που δεν μπορεί να εξηγηθεί από την εξελικτική θεωρία (και αφού γίνουν επανειλημμένες εκτιμήσεις της ηλικίας του απολιθώματος, ώστε να βεβαιωθούμε οτι δεν πρόκειται για λάθος μετρήσεων), θα έχουμε καταρρίψει τη θεωρία της εξέλιξης, την οποία θα πρέπει να διορθώσουμε ώστε να περιλαμβάνει και το νέο εύρημα. Κάνοντας στην πραγματικότητα χιλιάδες προβλέψεις σαν αυτές που αναφέρθηκαν, ασφαλώς και είναι διαψεύσιμη η θεωρία της εξέλιξης των ειδών, άρα και επιστημονική. Απλά δεν έχει διαψευστεί μέχρι σήμερα.
Τί μπορούμε όμως να πούμε για τη λεγόμενη θεωρία του “ευφυούς σχεδιασμού”, που λέει πάνω-κάτω οτι τα έμβια όντα μπορεί μεν να εξελίχθηκαν και να εξελίσσονται ως ένα βαθμό, αλλά σε κάποια κρίσιμα σημεία επενέβη ένας “ευφυής σχεδιαστής” ο οποίος παρήγαγε τα πιο πολύπλοκα από τα όργανα (όπως π.χ. τα μάτια), και χωρίς τον οποίο δεν θα υπήρχαμε σήμερα; Είναι αυτή η θεωρία διαψεύσιμη;
Αν το καλοσκεφτούμε, θα δούμε πως δεν είναι. Όποιος διαφωνεί δεν έχει παρά να προτείνει μια πρόβλεψη που κάνει η θεωρία αυτή, την οποία να μπορούμε να τη διαψεύσουμε μέσω μιας παρατήρησης, ακόμα κι αν στο τέλος αποτύχουμε να τη διαψεύσουμε· θα πρέπει να μας δίνεται η ευκαιρία όμως. Η θεωρία του ευφυούς σχεδιασμού δεν δίνει καμιά δυνατότητα διάψευσης κάποιας πρόβλεψής της — γιατί δεν κάνει προβλέψεις. Προσοχή: η υπόδειξη ενός ακόμη οργάνου που φαίνεται αρκετά πολύπλοκο (π.χ., το αυτί) δεν αποτελεί πρόβλεψη, αλλά απλώς υπόδειξη ενός αντικειμένου για το οποίο αυτός που το υποδεικνύει έχει άγνοια του πώς δημιουργήθηκε. Η προσωπική άγνοια ενός ατόμου για κάποιο γεγονός δεν συνεπάγεται το οτι το γεγονός αυτό συνέβη μέσω ενός θαύματος (δηλαδή καταστρατήγησης των φυσικών νόμων). Στην πραγματικότητα όταν κάποιος ισχυρίζεται οτι κάτι συνέβη μέσω θαύματος, δεν αφήνει περιθώριο για να διαψευστεί αυτός ο ισχυρισμός-του, γιατί η οντότητα που προκάλεσε το υποτιθέμενο θαύμα θα μπορούσε κάλλιστα να λάβει μέτρα ώστε να αποφευχθεί η οποιαδήποτε διάψευση. Άρα οποιαδήποτε θεωρία επικαλείται κάποια ανώτερη και εξωκοσμική ευφυΐα που έχει τη δύναμη και τις ικανότητες να παρακάμψει τον επιστημονικό έλεγχο, είναι αναγκαστικά μη επιστημονική.
Επίσης σημαντικό είναι να καταλάβουμε οτι το βάρος της υπόδειξης οτι μια θεωρία είναι διαψεύσιμη το σηκώνει εκείνος που προτείνει τη θεωρία. Δηλαδή, όποιος προτείνει τη θεωρία του “ευφυούς σχεδιασμού” για να εξηγήσει το πώς δημιουργήθηκαν τα έμβια όντα, αυτός είναι εκείνος που πρέπει να δείξει το πώς μπορεί να διαψευστεί η θεωρία-του, αν θέλει να ισχυριστεί οτι η θεωρία είναι επιστημονική. Αν δεν μπορεί να προτείνει κάποιον τρόπο με τον οποίο να διαψεύδεται η θεωρία, τότε δεν έχει μια επιστημονική θεωρία αλλά απλώς μια γνώμη. (Εγκυκλοπαιδικά, κανείς υποστηρικτής του “ευφυούς σχεδιασμού” δεν έχει προτείνει ποτέ το πώς η θεωρία αυτή μπορεί να διαψευστεί.)
Η λανθασμένη τάση προς επαλήθευση, παρά προς διάψευση
Είναι παρατηρημένο και γνωστό ψυχολογικό φαινόμενο οτι ο άνθρωπος τείνει να επιδιώκει την επιβεβαίωση μάλλον των απόψεών του (ή των επιστημονικών θεωριών-του), παρά τη διάψευσή τους. Αυτή η τάση και πρακτική είναι τελείως λανθασμένη, γιατί όσες επαληθεύσεις και να κάνουμε, δεν μπορούμε παρά να είμαστε προσεγγιστικά μόνο βέβαιοι για την αλήθεια της άποψης· ενώ αντίθετα αρκεί μία και μόνη διάψευση για να βεβαιωθούμε αμέσως για το λάθος. Επομένως, ο τίμιος επιστήμονας (αλλά και ο τίμιος νους που έχει κάποια άποψη γενικά για κάτι) πρέπει να επιδιώκει κυρίως τη διάψευση.
Ενδιαφέρον είναι οτι για το θέμα αυτό έγραψε ο Άγγλος φιλόσοφος Francis Bacon (Φράνσις Μπέικον, 1561–1626) από το 17ο αιώνα ακόμη (η τελευταία πρόταση μπήκε σε έντονη γραφή από το συγγραφέα του παρόντος):
“Η ανθρώπινη διάνοια, από τη στιγμή που θα υιοθετήσει μια άποψη (είτε επειδή είναι η κοινώς παραδεκτή είτε επειδή της είναι αρεστή), διαμορφώνει το καθετί κατά τρόπον ώστε να στηρίζει και να επιβεβαιώνει την άποψη αυτή. Όσο ισχυρές και πολλές και να είναι οι αποδείξεις περί του αντιθέτου, με μια βαριά και ολέθρια προκατάληψη τις αγνοεί και τις περιφρονεί ή τις εξαιρεί και τις απορρίπτει, επικαλούμενη κάποια διάκριση, προκειμένου να διαφυλαχθεί το κύρος των πρώτων παραδοχών. [...]” “Έτσι λειτουργούν όλες οι προλήψεις, είτε πρόκειται για την αστρολογία, τα όνειρα, τους οιωνούς, τη θεία δίκη, είτε για άλλο τι παρόμοιο· οι άνθρωποι, που αρέσκονται σε τέτοιες κενότητες, δίνουν σημασία στα γεγονότα όταν αυτά επαληθεύουν τις προβλέψεις τους, ενώ όταν κάτι τέτοιο δεν συμβαίνει — πράγμα που αποτελεί και τον κανόνα — τα παραβλέπουν και τα προσπερνούν. Αυτό το κακό, όμως, παρεισφρέει με πολύ πιο ύπουλο τρόπο στη φιλοσοφία και στις επιστήμες, όπου η αρχική άποψη αλλοιώνει και υποτάσσει εκείνην που έπεται, ακόμη και αν η τελευταία είναι ορθότερη και καλύτερα θεμελιωμένη. Εξάλλου, ανεξάρτητα από αυτή την τέρψη και την ελαφρότητα που περιέγραψα, είναι μόνιμο και χαρακτηριστικό σφάλμα της ανθρώπινης διάνοιας να συγκινείται και να διεγείρεται περισσότερο από την κατάφαση παρά από την άρνηση, ενώ κανονικά θα έπρεπε να αντιμετωπίζει καί τα δύο με τον ίδιο τρόπο. Για τη θεμελίωση μάλιστα ενός πραγματικού αξιώματος, μεγαλύτερη ισχύ έχει το αρνητικό παράδειγμα.” Francis Bacon, 1620: “Τα είδωλα της φυλής”, από το Νέο όργανο (Novum Organum). Απόσπασμα από το βιβλίο: “Η «εντολή» του Γαλιλαίου”, Edmund Blair Bolles· απόδοση στα ελληνικά: Διονύσης Γιαννίμπας· Πανεπιστημιακές Εκδόσεις Κρήτης, Ηράκλειο 2004. |
Κύρος επιστημόνων
Κανονικά υποτίθεται οτι το κύρος των επιστημόνων δεν πρέπει να παίζει κανένα ρόλο στο αν θα γίνει αποδεκτή η θεωρία ή όχι. Δεν έχει σημασία δηλαδή το ποιος είναι κανείς, αλλά το τί ισχυρίζεται. Αυτό είναι σημαντικό σαν κανόνας, γιατί απορρίπτει την αυθεντία σαν πηγή αλήθειας και πληροφόρησης. Ας θυμηθούμε οτι οι θρησκείες βασίζονται κατά κύριο λόγο στο κύρος της αυθεντίας προκειμένου να δεχτούν κάτι σαν σωστό. (Π.χ., «Εφόσον το είπε ο Μέγας [άγιος της Εκκλησίας], έπεται οτι είναι αλήθεια.») Στην επιστήμη δεν έχει σημασία το πρόσωπο που διατυπώνει μια άποψη, αλλά τα δεδομένα, και το αν αυτά συμφωνούν με την άποψη. Τα δεδομένα προηγούνται, οι απόψεις έπονται.
Στην πράξη όμως, όντως οι απόψεις επιστημόνων με κύρος προσέχονται περισσότερο από εκείνες άλλων που είναι άγνωστοι. Δεν αποφασίζεται βέβαια η αλήθεια βάσει του κύρους, αλλά δίνεται περισσότερη προσοχή όταν προτείνεται κάτι. Αυτό συμβαίνει γιατί είναι διαισθητικά κατανοητό οτι ο επιστήμονας δεν απέκτησε το κύρος-του αυθαίρετα, χωρίς λόγο, αλλά χάρη στις ικανότητές του. Το οτι έχει κύρος σημαίνει οτι οι προηγούμενες απόψεις-του έγιναν δεκτές ως επιστημονικά έγκυρες. Άρα υπάρχει αυξημενη πιθανότητα να είναι έγκυρες και οι τωρινές-του απόψεις. Το ζήτημα είναι οτι ο άρτια εκπαιδευμένος επιστήμονας γνωρίζει πώς να συνάγει έγκυρα συμπεράσματα, και η αυξημένη πιθανότητα του να συμβεί κάτι τέτοιο γίνεται σιωπηρά αποδεκτή από την υπόλοιπη επιστημονική κοινότητα. Πάντως πρόκειται απλώς για θέμα πιθανοτήτων να είναι σωστές οι απόψεις, και όχι για θέμα άκριτης αποδοχής-τους λόγω κύρους του παρατηρητή.
Ad hominem επιθέσεις
Ένα θέμα σχετικό με το κύρος των επιστημόνων είναι και οι ad hominem επιθέσεις. Στα λατινικά, ad hominem σημαίνει “κατά του ανθρώπου”. Η έκφραση χρησιμοποιείται όταν, αντί να επιχειρηματολογήσει κανείς βάσει της λογικής, ή βάσει των δεδομένων, κάνει επίθεση εναντίον του προσώπου που διατύπωσε μια θεωρία ή άποψη. Τυπικό παράδειγμα ad hominem επιθέσεων είναι οι προσπάθειες να αμαυρωθεί το όνομα του Charles Darwin (Δαρβίνου), προκειμένου να καταρριφθεί η θεωρία της εξέλιξης των ειδών. Μπορεί π.χ. να λεχθεί οτι ο Darwin τάχα αποκήρυξε τη θεωρία της εξέλιξης προς το τέλος της ζωής-του. Κάτι τέτοιο δεν συνέβη, αλλά σε κάθε περίπτωση είναι άσχετο με την ορθότητα ή μη της θεωρίας της εξέλιξης. Οι επιθέσεις αυτές γίνονται συνήθως από ανθρώπους που δεν έχουν ολοκληρωμένη εκπαίδευση στην επιστήμη, και γιαυτό δεν έχουν κατανοήσει οτι δεν έχει καμιά σημασία το τί πίστευε προσωπικά ο Χ επιστήμονας που πρότεινε μια θεωρία. Συνηθισμένοι στην “αλήθεια λόγω αυθεντίας” σε άλλους, μη επιστημονικούς τομείς, νομίζουν οτι το ίδιο ισχύει και στην επιστήμη. Στην πραγματικότητα, από τη στιγμή που μια ιδέα, άποψη, ή θεωρία διατυπωθεί, παύει να ανήκει πλέον σ’ εκείνον που τη διατύπωσε· ανήκει σ’ ολόκληρη την ανθρωπότητα, η οποία είναι σε θέση να ελέγξει το κατά πόσο είναι σωστή, ανεξάρτητα από το τί πιστεύει πλέον αυτός ο οποίος έκανε την αρχική διατύπωση.
Έλεγχος ισχυρισμών μέσω αναφοράς σε πηγές
Όταν ένας επιστήμονας γράφει ένα άρθρο προς δημοσίευση, οφείλει να υποστηρίζει κάθε σημείο το οποίο ισχυρίζεται μέσω αναφορών σε προηγούμενες δημοσιεύσεις (άλλων, ή και δικές-του). Ακόμη και αν είναι σίγουρος για την ορθότητα των ισχυρισμών-του, και πάλι πρέπει να κάνει αναφορές σε δημοσιεύσεις, για δύο λόγους:
-
μπορεί παρά τη βεβαιότητά του, να κάνει λάθος
 · ή
· ή -
μπορεί να μην είναι βέβαιος ο αναγνώστης
Αυτό το δεύτερο σημείο έχει μεγάλη σημασία, καθώς δεν γνωρίζουμε ποτέ το τί γνωρίζει ο αναγνώστης· επομένως πρέπει να του δίνουμε την ευκαιρία να ανατρέξει στις πηγές ώστε να διαλυθεί κάθε-του αμφιβολία. Επιπλέον, με την αναφορά σε πηγές ο συγγραφέας “αίρει από τους ώμους-του” την ευθύνη των όσων υποστηρίζει· υπεύθυνοι είναι πλέον οι συγγραφείς της πηγαίας δημοσίευσης, και όσοι την αποδέχτηκαν ως δημοσιεύσιμη. Φυσικά, αν η πηγή έχει λάθος, έπεται οτι αντίστοιχα λάθος είναι και το άρθρο που αναφέρεται σ’ αυτές. Άρα δεν κάνουμε άκριτα αναφορές σε πηγές, αλλά επιλέγουμε προσεκτικά τις δημοσιεύσεις στις οποίες βασιζόμαστε.
Γιατί ο επιστήμονας είναι σκεπτικιστής
Ας υποθέσουμε οτι μαθαίνουμε πως σε κάποια συγκέντρωση μερικών ανθρώπων σε ένα σπίτι, κάποιος από την παρέα έκανε επίδειξη “ψυχικών δυνάμεων” (χωρίς να δηλώσει οτι «είμαι ταχυδακτυλουργός»), είτε λυγίζοντας κουτάλια “με τη δύναμη του πνεύματος”, είτε κάνοντας αντικείμενα να υψωθούν από το έδαφος και να μείνουν μετέωρα, και πάλι με την ίδια δύναμη.
Γιατί οι επιστήμονες ακούνε τέτοιους ισχυρισμούς με πολύ σκεπτικισμό;
Διότι ο επιστήμονας, ιδίως αν είναι φυσικός, γνωρίζει ποιες δυνάμεις υπάρχουν στη φύση. Είναι ακριβώς τέσσερις: η βαρυτική, η ηλεκτρομαγνητική, η ασθενής, και η ισχυρή πυρηνική. Αυτές είναι, δεν υπάρχει καμία άλλη που να γνωρίζουμε μέχρι στιγμής, και βέβαια σ’ αυτές δεν περιλαμβάνεται καμία υποτιθέμενη “ψυχική” δύναμη.
Είπαμε όμως «καμία άλλη που να γνωρίζουμε μέχρι στιγμής». Κι αν υπάρχει “ψυχική δύναμη” που δεν τη γνωρίζουμε μέχρι τώρα;
Εδώ, η σκέψη του επιστήμονα (που είναι υποσυνείδητη και δημιουργεί το σκεπτικισμό) είναι η εξής: «Είναι δυνατόν ποτέ, εκατομμύρια επιστήμονες σ’ όλο τον κόσμο, Νομπελίστες φυσικοί, ή άλλοι που υπήρξαν από τους πιο ευφυείς ανθρώπους που περπάτησαν ποτέ στη γη — συμπεριλαμβανομένων διανοιών της φυσικής όπως ο Αϊνστάιν, ο Bohr, ο Heisenberg, ο Feynman, ο Hawking, και τόσοι άλλοι — να έχουν κάνει λάθος πιστεύοντας οτι οι δυνάμεις στη φύση είναι μόνο τέσσερις, ενώ ο Χ που ισχυριζεται οτι έχει “ψυχικές δυνάμεις” να έχει δίκιο;» Ασφαλώς η υποτιθέμενη “ψυχική” δύναμη, αν υπήρχε, θα ήταν κι αυτή μια δύναμη της φύσης, εφόσον κινεί φυσικά αντικείμενα· άρα θα μπορούσε να εξεταστεί στο εργαστήριο. Έλα όμως που κανένας φυσικός δεν έχει μπορέσει ποτέ να την παρατηρήσει! Η υποσυνείδητη επιστημονική σκέψη λοιπόν είναι πως είναι εξαιρετικά περιορισμένες οι πιθανότητες να έχουν λάθος όλοι οι φυσικοί και οι πιο νοήμονες άνθρωποι του κόσμου, και να έχει δίκιο ο Χ άνθρωπος που ισχυρίζεται οτι έχει — άγνωστες μέχρι τώρα — “ψυχικές δυνάμεις”. Άλλωστε, αν είχε πράγματι τέτοιες δυνάμεις, θα μπορούσε να ανοίξει ένα άγνωστο μέχρι στιγμής κεφάλαιο της φυσικής, κερδίζοντας τεράστια φήμη, ένα βραβείο Νόμπελ, και πάρα-πάρα πολλά χρήματα. Άρα “κάποιο λάκκο έχει η φάβα” — που είναι το απόφθεγμα του σκεπτικιστή.
Παράδειγμα περίπτωσης ανθρώπου που ισχυρίζεται οτι έχει υπερφυσικές (“ψυχικές”) δυνάμεις αποτελεί ο γνωστός “πνευματιστής” Ούρι Γκέλλερ (Uri Geller). Στο παρακάτω βίντεο, που σχολιάζει ο Καναδός “ξεσκεπαστής τσαρλατάνων” Τζέιμς Ράντι (James Randi), βλέπουμε τον Γκέλλερ να είναι καλεσμένος στο “The Tonight Show” του Αμερικανού τηλεπαρουσιαστή και κωμικού Τζόννυ Κάρσον (Johnny Carson — απεβίωσε το 2005). Ο Κάρσον, που κάποτε ήταν και ο ίδιος ταχυδακτυλουργός, και πίστευε οτι ο Γκέλλερ ήταν ένας μεγάλος απατεώνας, πήρε τηλέφωνο τον Ράντι πριν από τα γυρίσματα της εκπομπής, και ζήτησε τη συμβουλή-του. Ακολουθώντας τις συμβουλές του Ράντι, ο Κάρσον και οι συνεργάτες-του ετοίμασαν στο στούντιο μια σειρά από μικρά βαζάκια, όλα ερμητικά κλειστά, τα οποία βλέπουμε στο τραπεζάκι μπροστά στον Γκέλλερ. Ένα από τα βαζάκια είχε νερό, ενώ τα άλλα ήσαν άδεια. Ο Γκέλλερ θα έπρεπε απλώς να μαντέψει ποιο βαζάκι είχε το νερό, κάτι το οποίο είχε επιδείξει πολλές φορές μέχρι τότε (αλλά πάντοτε με δικά-του βαζάκια και φυσικά με δικούς-του όρους διεξαγωγής του θεάματος). Ας δούμε τη συνάντηση Κάρσον–Γκέλλερ:
| Σημείωση: για ελληνικούς υπότιτλους, αφού ξεκινήσετε το βίντεο, πατήστε το κόκκινο πλήκτρο με την ένδειξη CC → |
|
Το προηγούμενο παράδειγμα με τις “ψυχικές δυνάμεις” γενικεύεται σε οποιονδήποτε παρόμοιο ισχυρισμό. Κάθε ισχυρισμός που αντίκειται στους νόμους της φύσης, στην πραγματικότητα αντίκειται σ’ ένα γιγαντιαίο οικοδόμημα. Το πόσο γιγαντιαίο είναι αυτό το οικοδόμημα — και κατά συνέπεια πόσο δύσκολη η ανατροπή-του — είναι πολύ δύσκολο να το καταλάβει ο μη-επιστήμονας. Γιαυτό και οι αιτιάσεις περί μυστηριωδών δυνάμεων γίνονται πολύ πιο εύκολα αποδεκτές από το μη ειδικό. Αντίθετα, ο ειδικός γνωρίζει οτι αυτός που υποστηρίζει οτι πήγε ενάντια στους γνωστούς νόμους της φυσικής κάνει το ανάλογο ενός ανθρώπου που ισχυρίζεται οτι με μια κλωτσιά κατέρριψε ένα οικοδόμημα που στεκόταν μπροστά-του, χωρίς να αντιλαμβάνεται οτι το οικοδόμημα που τάχα κατέρριψε έχει μέγεθος ουρανοξύστη, και οτι τέτοια οικοδομήματα είναι πλέον μάλλον αδύνατο να κατεδαφιστούν με τη δύναμη ενός ανθρώπου.
Η θεμελιώδης παραδοχή περί φυσικότητας
Το προηγούμενο παράδειγμα με τον ισχυρισμό περί ύπαρξης “ψυχικών δυνάμεων” που κινούν αντικείμενα μας οδηγεί σε μια επιπλέον σημαντική ιδέα:
|
Οτιδήποτε είναι σε θέση να επιδράσει πάνω σε φυσικά αντικείμενα υπόκειται σε επιστημονική έρευνα. |
Αυτό σημαίνει οτι εάν κάποιος ισχυρίζεται οτι λυγίζει κουτάλια “με τη δύναμη του πνεύματος”, και αφού μπορεί να το κάνει αυτό κατ’ επανάληψη (άρα αυτό που κάνει είναι επαληθεύσιμο), είναι ελεύθερος να περάσει από το εργαστήριο του φυσικού για να ελεγχθούν τα φυσικά φαινόμενα που προκαλεί κάτω από εργαστηριακές συνθήκες.
Στην πράξη βέβαια κανείς απ’ όσους ισχυρίζονται κατάρριψη ή ανεπάρκεια των γνωστών νόμων της φυσικής δεν πηγαίνει ποτέ στο εργαστήριο, ή δεν αφήνει το εργαστήριο να εγκατασταθεί κοντά-του, γιατί έχει να χάσει πολλά από την αποκάλυψη του τεχνάσματός του, ενώ κερδίζει πολύ περισσότερα όσο οι “δυνάμεις-του” παραμένουν ανεξιχνίαστες, στη σφαίρα του μυστηρίου.
Φυσικά η παραπάνω πρόταση εντός του πλαισίου δεν αφορά μόνο στις υποτιθέμενες “ψυχικές δυνάμεις”, αλλά και σε οτιδήποτε το “μεταφυσικό”: εφόσον το μεταφυσικό έχει κάποιο αποτέλεσμα στον φυσικό κόσμο, έπεται οτι και το μεταφυσικό είναι υποψήφιο για να υποστεί την επιστημονική έρευνα. Αν π.χ. κάποιος άνθρωπος ισχυρίζεται οτι ακούει φωνές, ή βλέπει οράματα, ή επικοινωνεί με τους νεκρούς, ή με το Θεό, κλπ., δεν ισχυρίζεται πράγματα που είναι “εκτός ορίων” της επιστήμης, αφού ο εγκέφαλός του που είναι τάχα δέκτης τέτοιων μηνυμάτων είναι μέρος της φύσης. Άρα οι επιστήμονες έχουν τη δυνατότητα να εξετάσουν τον εγκέφαλό του την ώρα που ο άνθρωπος έχει τις εμπειρίες αυτές, ώστε να προσπαθήσουν να εξηγήσουν πώς αυτές συμβαίνουν. Και πράγματι, έχουν γίνει και γίνονται τέτοιες έρευνες, και τα συμπεράσματα είναι μέχρι στιγμής πολύ ενδιαφέροντα. (Το ενδιαφέρον βρίσκεται στην κατανόηση του πώς ο εγκέφαλος καταφέρνει να δημιουργεί παραισθήσεις, και να ξεγελάει τον εαυτό-του — αυτά εξετάζονται στο μάθημα Ν4.) Δεν ισχύει λοιπόν το οτι υπάρχουν κάποια υποτιθέμενα “όρια” τα οποία δεν πρέπει να υπερβεί η επιστήμη. (Γιατί “δεν πρέπει” άραγε;) Τα όρια αυτά φαίνονται να τα θέτουν μόνο όσοι φοβούνται την απομυθοποίηση των όσων πιστεύουν.
Η “φιλοσοφία” του επιστήμονα, και οι επιστημονικές “πίστεις”
Οι επιστήμονες έχουν κάποιες βαθειά ριζωμένες αρχές, που κανείς δεν τους τις διδάσκει άμεσα, αλλά τις μαθαίνουν έμμεσα από την ενασχόλησή τους με την επιστήμη.
Εδώ όμως να ανοίξουμε μια μικρή παρένθεση για να τονίσουμε οτι όταν λέμε “πίστη” (την οποία σημειώνουμε σε εισαγωγικά) δεν εννοούμε στην κυριολεξία την πίστη του θρησκευόμενου ανθρώπου, που δεν αμφιβάλλει ποτέ αυτό που πιστεύει· εννοούμε “πίστη” όπως “παραδοχή με μεγάλη — όχι όμως απόλυτη — βεβαιότητα”.
Η “πίστη” στην αντικειμενικότητα της φύσης
Βαθιά ριζωμένη στο υποσυνείδητο του επιστήμονα είναι η ιδέα οτι ο φυσικός κόσμος υπάρχει “εκεί έξω”, εκτός του παρατηρητή, και οτι είναι αντικειμενικά παρατηρήσιμος. Δηλαδή, αν δύο παρατηρητές παρατηρούν τον κόσμο, θα πρέπει να συμφωνήσουν με την ένδειξη των επιστημονικών οργάνων. Το αν, για παράδειγμα, μια πέτρα είναι πιο ζεστή από μια άλλη, δεν είναι κάτι που αποφασίζει ο Χ ή ο Ψ επιστήμονας, αλλά ένα θερμόμετρο. Το θερμόμετρο, στην προκειμένη περίπτωση, έχει μεγαλύτερο “κύρος” από την άποψη του οποιουδήποτε, όσο ιδιοφυής κι αν είναι αυτός — αυτό σημαίνει “αντικειμενικότητα”.
Γενικά, λόγω της πίστης στην αντικειμενικότητα της φύσης, ο επιστήμονας εμπιστεύεται τις ενδείξεις των εργαλείων-του και των μετρητών-του περισσότερο από τη γνώμη του οποιουδήποτε. Γιαυτό λέμε οτι στην επιστήμη “τα δεδομένα προηγούνται, οι θεωρίες έπονται”.
Ας σημειωθεί οτι στο 2ο μισό του 20ού αιώνα εμφανίστηκε μια αποκλίνουσα άποψη μεταξύ κυρίως φιλοσόφων, αλλά και μεταξύ αρκετών επιστημόνων του τομέα της κβαντικής φυσικής. Δηλαδή επικράτησε η λανθασμένη άποψη οτι “ο παρατηρητής επηρεάζει μέσω της παρατήρησής του το αποτέλεσμα του πειράματος”, και άρα “ο ανθρώπινος νους δημιουργεί την πραγματικότητα”. Σήμερα όμως έχει γίνει κατανοητό οτι “παρατηρητής” δεν είναι υποχρεωτικά ένας νους, δηλαδή ένα συνειδητό ον· “παρατηρητής” μπορεί να είναι και ένα μόριο ύλης, το οποίο επίσης “δημιουργεί την πραγματικότητα”. Οι απόψεις των κβαντικών φυσικών του 20ού αιώνα βασίστηκαν σε μια απλοϊκή και λαθεμένη άποψή τους περί “συνειδητότητας”, μια έννοια που ποτέ δεν όρισαν — επόμενο είναι, αφού βγαίνει εκτός των ορίων της κβαντικής φυσικής. Το ένα λάθος λοιπόν βρίσκεται στο οτι δεν υπάρχει τρόπος να βάλουμε μια διαχωριστική γραμμή και να ορίσουμε το ποιος παρατηρητής είναι συνειδητός και ποιος όχι (άρα το ποιος υποτιθέμενα δημιουργεί την πραγματικότητα και ποιος όχι)· και το δεύτερο λάθος είναι οτι, όπως ειπώθηκε, την ιδιότητα του “παρατηρείν” την έχει γενικά η ύλη, άρα είναι άτοπο να τίθεται θέμα συνειδητής παρατήρησης, και άρα υποκειμενικής τάχα δημιουργίας της πραγματικότητας. Το θέμα αυτό εξετάζεται διεξοδικότερα στο μάθημα Φ3 του Δ.Ε.Π. (“Εισαγωγή στην κβαντική φυσική”).
Η “πίστη” στην κατανοησιμότητα της φύσης
Μια άλλη “πίστη” των επιστημόνων είναι οτι ο κόσμος είναι κατά βάθος κατανοήσιμος. Δηλαδή κάθε ερώτημα που αφορά στον κόσμο έχει κάποια επιστημονική απάντηση. Μπορεί την απάντηση αυτή να μην την έχουμε βρει μέχρι τώρα, αλλά προσπαθώντας και ψάχνοντας, κάποτε θα τη βρούμε. Παράδειγμα: μπορεί να μη γνωρίζουμε σήμερα πώς ο μουσικοσυνθέτης δημιουργεί μια καινούργια μελωδία, ή πώς έρχεται η έμπνευση στο ζωγράφο που ζωγραφίζει έναν πίνακα, οπότε λέμε οτι η τέχνη είναι μέχρι στιγμής εκτός ορίων της επιστήμης. Είναι όμως γενικά παραδεκτό μεταξύ των επιστημόνων οτι κάποτε, μετά από πολλές δεκαετίες ίσως, θα πλησιάσουμε τις απαντήσεις σε όλα τα ερωτήματα που αφορούν στον φυσικό κόσμο.
Ας σημειωθεί οτι η πίστη στην κατανοησιμότητα μπορεί να είναι και λάθος. Μπορεί (και ίσως έτσι είναι) ο ανθρώπινος νους να έχει κάποια όρια από τη φύση-του τα οποία δεν μπορεί να υπερνικήσει. Ίσως ζούμε στην εποχή που μόλις έχουν αρχίσει να γίνονται ορατά τα όρια αυτά. Προς το παρόν όμως οι περισσότεροι επιστήμονες επιμένουν στην ιδέα οτι ο κόσμος είναι κατανοήσιμος.
Η “πίστη” στη λιτότητα της φύσης
Μια άλλη παρόμοια “πίστη” όπως η προηγούμενη είναι και η εξής: ο επιστήμονας πιστεύει οτι η φύση είναι κατά βάθος απλή, και οτι όταν κάτι μας φαίνεται πολύπλοκο, αυτό γίνεται γιατί το μυαλό-μας μας “μπερδεύει” προσωρινά, γιατί δεν μπορεί να δει τα πράγματα “από άλλη οπτική γωνία”, από την οποία θα φαίνονταν απλούστερα.
Τυπικό παράδειγμα η αντικατάσταση του γεωκεντρικού μοντέλου (που ήθελε τη Γη στο κέντρο του σύμπαντος), από το ηλιοκεντρικό μοντέλο, που έχει τη Γη να περιφέρεται γύρω από τον Ήλιο. Το γεωκεντρικό μοντέλο ήθελε τις τροχιές των πλανητών όπως ο Ερμής, η Αφροδίτη, ο Άρης, κλπ., να είναι εξαιρετικά πολύπλοκες: όπως φαίνονται από τη Γη (αν τη θεωρήσουμε ακίνητη), οι πλανήτες αυτοί κάποτε κινούνται προς μία διεύθυνση, κάποτε όμως μοιάζουν να “φρενάρουν”, να σταματούν, και να γυρίζουν ανάποδα, κινούμενοι προς την αντίθετη διεύθυνση· μετά ξαναφρενάρουν, και γυρίζουν πάλι προς την αρχική διεύθυνση· κ.ο.κ. Στην πραγματικότητα αυτό είναι μια οπτική απάτη, που συμβαίνει επειδή οι “εσωτερικοί” πλανήτες (δηλαδή ο Ερμής και η Αφροδίτη, που είναι πιο κοντά στον Ήλιο από τη Γη) κινούνται ταχύτερα από τη Γη, την οποία φτάνουν και ξεπερνούν· μόλις φτάσουν στην ανώτατη απόσταση από τον Ήλιο (από τη δική-μας οπτική γωνία), φαίνονται σαν να κάνουν στροφή και να κινούνται προς την αντίθετη διεύθυνση στον ουράνιο θόλο. Αντίστοιχα, η Γη κινείται ταχύτερα από τους “εξωτερικούς” πλανήτες Άρη, Δία, και Κρόνο, τους οποίους “προσπερνάει”, οπότε έχουμε το αντίστροφο φαινόμενο. Οι αρχαίοι Έλληνες (π.χ. ο Αριστοτέλης και μετέπειτα ο Πτολεμαίος), επειδή είχαν το γεωκεντρικό μοντέλο κατά νου, συμπέραναν οτι οι πλανήτες κινούνται βάσει πολύπλοκων καμπυλών που ονομάζονται “επικυκλοειδείς” στα μαθηματικά. Αυτές είναι οι καμπύλες που διαγράφουν σημεία ενός κύκλου που κυλάει πάνω σε έναν άλλον κύκλο.
Παράδειγμα επικυκλοειδούς καμπύλης
Με το πιο σωστό ηλιοκεντρικό μοντέλο όμως, οι τροχιές απλοποιούνται κατά πολύ, και από επικυκλοειδείς γίνονται απλοί κύκλοι, όπως υπέθεσαν ο Αρίσταρχος ο Σάμιος και ο Κοπέρνικος· ή σχεδόν κύκλοι, δηλαδή ελλείψεις, όπως συμπέρανε λίγο αργότερα ο Κέπλερ, αφού εξέτασε προσεκτικά τα δεδομένα.
Παράδειγμα έλλειψης
Αυτή η απλοποίηση της φυσικής θεωρίας συνέβη άλλη μια φορά μόλις έναν αιώνα πριν, όταν ο Αϊνστάιν διατύπωσε τη θεωρία της γενικής σχετικότητας. Με τη θεωρία αυτή, οι τροχιές των πλανητών ενώ μας φαίνονται σαν “αργά περιστρεφόμενες ελλείψεις” — αν θέλουμε να είμαστε ακριβείς — στην πραγματικότητα είναι απλώς ευθείες γραμμές, αλλά “ευθείες” σε ένα χώρο τεσσάρων διαστάσεων (το χωροχρόνο). Δηλαδή συνέβη και πάλι μια απλοποίηση, αλλά για να κατανοήσουμε την απλοποίηση αυτή πρέπει να ξεφύγουμε από το πώς αντιλαμβάνεται τα πράγματα ο νους μέσω της καθημερινής εμπειρίας, και να πάμε σε ένα χώρο μαθηματικό, του οποίου δεν έχουμε άμεση γεωμετρική αντίληψη.
Τροχιές πλανητών σαν περιστρεφόμενες ελλείψεις, βάσει της θεωρίας της γενικής σχετικότητας
Αντίστοιχες απλοποιήσεις συνέβησαν στη φυσική όταν έγινε κατανοητό οτι ο ηλεκτρισμός και ο μαγνητισμός στην πραγματικότητα είναι δυο όψεις του ίδιου φαινομένου: αποτελέσματα της ηλεκτρομαγνητικής δύναμης. Στον αιώνα που πέρασε έγινε άλλη μια “ενοποίηση” (διάβαζε: απλοποίηση), όταν και η ισχυρή και η ασθενής πυρηνική δύναμη έγιναν κατανοητές σαν εκφάνσεις της ίδιας θεμελιώδους δύναμης που αποτέλεσμά της είναι και η ηλεκτρομαγνητική. Έτσι τώρα έχουμα μία θεωρία που εξηγεί τις τρεις από τις τέσσερις δυνάμεις της φύσης, και έχει μείνει έξω από τη θεωρία αυτή μόνο η τέταρτη δύναμη: η βαρυτική. Οι επιστήμονες, με την πίστη που έχουν στην απλότητα της φύσης, προσπαθούν κατά τις δεκαετίες που διανύουμε να ενοποιήσουν και τη βαρυτική δύναμη στο ίδιο μοντέλο, ώστε να έχουμε μια και μοναδική θεωρία που να εξηγεί καί τις τέσσερις δυνάμεις (τη λεγόμενη “θεωρία των πάντων”). Το αν θα το πετύχουν ή όχι είναι άσχετο με το παρόν θέμα· αυτό που παρατηρούμε είναι οτι η πίστη-τους στην απλότητα της φύσης τους οδηγεί στο να προσπαθούν ν’ ανακαλύψουν την απλούστερη δυνατή θεωρία. Το πρακτικό αντίκτυπο είναι οτι ξοδεύονται ποσά κατά εκατομμύρια επειδή υπάρχει η πίστη αυτή, που οδηγεί την έρευνα προς συγκεκριμένες κατευθύνσεις.
Η πίστη στην απλότητα έχει εκφραστεί ήδη από το 14ο αιώνα, από τον Άγγλο φιλόσοφο William of Ockham ή Occam (Όκαμ), που διατύπωσε το περίφημο “ξυράφι του Όκαμ”, το οποίο λέει το εξής:
|
Ξυράφι
του Όκαμ: |
Παραδείγματα σχετιζόμενα με θρησκευτικές απόψεις:
-
Κατά το Μεσαίωνα οι χριστιανοί θεολόγοι πίστευαν οτι οι πλανήτες κινούνται πάνω στις τροχιές-τους επειδή υπάρχουν άγγελοι που τους σπρώχνουν. Από τη στιγμή που έγινε κατανοητή όμως η θεωρία της κίνησης των πλανητών (μέσω των νόμων του Κέπλερ και της βαρυτικής θεωρίας του Νεύτωνα, αλλά και της μετέπειτα συμπλήρωσής της από τον Αϊνστάιν), οι άνθρωποι κατάλαβαν οτι οι άγγελοι δεν χρειάζονται, γιατί και χωρίς την ύπαρξή τους, πάλι οι πλανήτες θα κινούνταν όπως τους βλέπουμε να κινούνται. Οι άγγελοι λοιπόν “κόπηκαν” από τη θεωρία με το ξυράφι του Όκαμ.
-
Ακόμη και μέχρι τις ημέρες-μας, ο μέσος άνθρωπος πιστεύει οτι ο Θεός έφτιαξε τα άστρα (ή εξακολουθεί να τα φτιάχνει, όταν μαθαίνουν οτι άστρα εξακολουθούν να δημιουργούνται διαρκώς στο γαλαξία-μας). Όταν όμως γίνεται κατανοητό το πώς η διαστρική σκόνη κατακρημνίζεται κάτω από της επίδραση του ίδιου-της του βάρους, και συγκεντρώνεται σε μερικά σημεία όπου δημιουργούνται τα άστρα (σε διάρκεια πολλών εκατομμυρίων ετών), τότε η δράση του Θεού περιττεύει, γιατί και τίποτα να μην κάνει ο Θεός (αν υπάρχει), και πάλι θα δημιουργηθούν άστρα, όπως δημιουργούνται οι σταγόνες της βροχής μέσα σε ένα πυκνό σύννεφο, και πέφτουν προς τη γη. Το ξυράφι του Όκαμ λοιπόν “κόβει” και το Θεό απο τη δημιουργία των άστρων. (Φυσικά συγκεκριμένα από τη δημιουργία των άστρων — ας μην παρερμηνευθεί αυτή η παρατήρηση, γενικευόμενη αβάσιμα.)
Ας δούμε και ένα πιο αφηρημένο παράδειγμα. Είδαμε σε προηγούμενη ενότητα οτι έχοντας τους αριθμούς 2, 9, 14, 17, 18, 17, 14, 9, και 2, και τοποθετώντας-τους σαν κουκκίδες ανά τακτά διαστήματα ανάλογα με το ύψος-τους, μπορούμε να τους “συνοψίσουμε” με μια καμπύλη:

Η καμπύλη αυτή είναι η “θεωρία” που περιγράφει (και συνοψίζει) τους αριθμούς, και φαίνεται αρκετά λιτή. Μπορεί όμως να πει κανείς οτι αντί για την παραπάνω, θα μπορούσαμε να περιγράψουμε τα δεδομένα με την εξής καμπύλη:
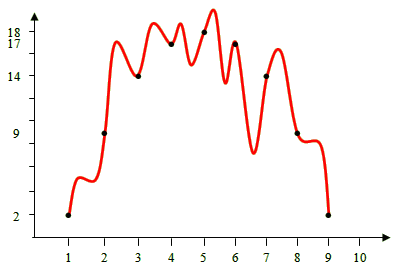
Κι αυτή η καμπύλη, στο κάτω-κάτω, περνάει από όλα τα δεδομένα, άρα τα περιγράφει σωστά. Απλώς είναι λίγο “αλλοπρόσαλλη” σε όλα τα άλλα σημεία εκτός των δεδομένων. Γιατί όμως να μην είναι αυτή η σωστή θεωρία που να περιγράφει όλα τα δεδομένα;
Εάν έχουμε τη δυνατότητα να συλλέξουμε
επιπλέον δεδομένα, μπορούμε να δούμε ποια από τις δύο θεωρίες — η απλή ή
η πολύπλοκη — τα περιγράφει σωστά. Αν όμως δεν έχουμε αυτή τη
δυνατότητα, ή ξέρουμε οτι για να συλλέξουμε επιπλέον δεδομένα πρέπει να
περιμένουμε για τεχνολογία του μέλλοντος, τότε κανείς δεν μπορεί να
αποκλείσει οτι η πολύπλοκη είναι η σωστή θεωρία. Μπορούμε όμως,
χάρη στην πίστη για τη λιτότητα της φύσης, να απορρίψουμε με το ξυράφι
του Όκαμ — προς το παρόν τουλάχιστον — την πολύπλοκη, προτιμώντας την
απλούστερη καμπύλη. Επίσης, αυτό που συζητάμε δεν είναι θέμα απλώς μιας
απλής ή μιας πολύπλοκης καμπύλης. (Γιατί τί σημαίνει άλλωστε “απλή” ή
“πολύπλοκη” καμπύλη;) Ο αναγνώστης θα θυμάται ίσως οτι η πρώτη καμπύλη
(η απλή) περιγράφεται από τη συνάρτηση: “y = 18 – (x – 5)2![]() ”.
Η δεύτερη καμπύλη (η πολύπλοκη) περιγράφεται κι αυτή από κάποια
συνάρτηση, που όμως αν προσπαθήσουμε να καταγράψουμε, θα διαπιστώσουμε
οτι ξεπερνάει σε μήκος μία σειρά αυτής της σελίδας. (Για όσους έχουν το
μαθηματικό υπόβαθρο, είναι ένα πολυώνυμο 16ου
βαθμού.) Δεν είναι λοιπόν μόνο η καμπύλη οπτικά πιο πολύπλοκη,
αλλά πολύπλοκος είναι και οποιοσδήποτε άλλος τρόπος περιγραφής της θεωρίας αυτής (π.χ.
μέσω συναρτήσεων). Αυτό συμβαίνει γιατί η δεύτερη θεωρία είναι
εγγενώς πιο πολύπλοκη από την πρώτη. Το σκεπτικό της απόρριψής της
είναι οτι εφόσον το ξυράφι του Όκαμ έχει δουλέψει σωστά πάμπολλες φορές
στο παρελθόν, επόμενο είναι να αναμένουμε να δουλέψει και πάλι στο
μέλλον — χωρίς όμως ποτέ να είμαστε βέβαιοι οτι έτσι πρέπει να
είναι.
”.
Η δεύτερη καμπύλη (η πολύπλοκη) περιγράφεται κι αυτή από κάποια
συνάρτηση, που όμως αν προσπαθήσουμε να καταγράψουμε, θα διαπιστώσουμε
οτι ξεπερνάει σε μήκος μία σειρά αυτής της σελίδας. (Για όσους έχουν το
μαθηματικό υπόβαθρο, είναι ένα πολυώνυμο 16ου
βαθμού.) Δεν είναι λοιπόν μόνο η καμπύλη οπτικά πιο πολύπλοκη,
αλλά πολύπλοκος είναι και οποιοσδήποτε άλλος τρόπος περιγραφής της θεωρίας αυτής (π.χ.
μέσω συναρτήσεων). Αυτό συμβαίνει γιατί η δεύτερη θεωρία είναι
εγγενώς πιο πολύπλοκη από την πρώτη. Το σκεπτικό της απόρριψής της
είναι οτι εφόσον το ξυράφι του Όκαμ έχει δουλέψει σωστά πάμπολλες φορές
στο παρελθόν, επόμενο είναι να αναμένουμε να δουλέψει και πάλι στο
μέλλον — χωρίς όμως ποτέ να είμαστε βέβαιοι οτι έτσι πρέπει να
είναι.
Από την αρχαιότητα, η ελληνική σκέψη εξέφραζε την πίστη στη λιτότητα της φύσης, καθώς οι αρχαίοι Έλληνες φυσικοί φιλόσοφοι προσπαθούσαν να εξηγήσουν την εξαιρετική πολυπλοκότητα που παρατηρούμε στη φύση μέσω της αναγωγής σε απλές στοιχειώδεις ουσίες: ο Θαλής μέσω του νερού, ο Ηράκλειτος μέσω της φωτιάς, ο Πυθαγόρας μέσω των αριθμών, ο Εμπεδοκλής — και αργότερα ο Αριστοτέλης — μέσω της θεωρίας των τεσσάρων στοιχείων (πυρ, αέρας, γη, νερό), ο Δημόκριτος μέσω των ατόμων, κλπ. Αυτή η ελληνική παράδοση της πίστης στη λιτότητα συνεχίστηκε και αργότερα στη Δυτική σκέψη, με την ανακάλυψη των 92 φυσικών στοιχείων (ατόμων), την ενοποίηση των δυνάμεων (βλ. παραπάνω), κλπ. Τα θέματα αυτά εξετάζονται πιο διεξοδικά στο μάθημα Ε2.
Άσκηση
Με βάση τα όσα έγιναν κατανοητά συνολικά από το μάθημα αυτό, προσπαθήστε να απαντήσετε το παρακάτω ερώτημα:
| Εφόσον οι επιστήμονες έχουν — όπως όλοι οι άνθρωποι — υποκειμενική αντίληψη, δεν είναι το επιστημονικό οικοδόμημα κι αυτό αναγκαστικά υποκειμενικό, και ίσως φτιαγμένο από την κοινωνικά κατασκευασμένη αντίληψη των επιστημόνων; |
Σημείωση: η παραπάνω είναι επίσης γνωστή ως “θέση του Φάιεράμπεντ (
Feyerabent)”.Πίσω στη γενική σελίδα του Διαδικτυακού Επιστημονικού Πανεπιστημίου