 |
Ιστορία και Εξέλιξη της ΕπιστήμηςΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ Ε2 ΤΟΥ Δ.Ε.Π. |
Η “χειμερία νάρκη του πνεύματος” κατά το Μεσαίωνα
Μετά από την εκπληκτική άνθηση του πνεύματος κατά την προεπιστημονική εποχή των αρχαίων Ελλήνων, η μετέπειτα περίοδος 15 περίπου αιώνων μοιάζει — μετά από σύγκριση — σαν ένα απέραντο χρονικό τέλμα, όπου πρακτικά καμία κοσμοϊστορική ανακάλυψη δεν έγινε, καμία νέα θεωρία της φύσης δεν προτάθηκε, καμία από τις παλαιές θεωρίες δεν βελτιώθηκε. Οι λόγοι για τους οποίους συνέβει αυτή η “πνευματική καθίζηση” είναι κοινωνικοπολιτικοί, και ίσως θρησκευτικοί, πάντως εκτός του εύρους του παρόντος μαθήματος. Δύο είναι τα πιο σημαντικά γεγονότα που σχετίζονται με την εξέλιξη της επιστήμης την περίοδο αυτή: η μετατόπιση του κέντρου της πνευματικής δραστηριότητας στον Ισλαμικό κόσμο, και η ανάπτυξη της αλχημείας.
Ισλαμικός πολιτισμός
Από τον 8ο μέχρι τον 13ο αιώνα, και για μερικούς μελετητές μέχρι και το 15ο, σημειώθηκε μια κάποια ανάπτυξη του πνεύματος στον Ισλαμικό κόσμο, ο οποίος εκτεινόταν από την Ισπανία μέχρι το σημερινό Πακιστάν κατά τον 8ο αιώνα, αποτελώντας έτσι μια από τις μεγαλύτερες αυτοκρατορίες όλων των εποχών.
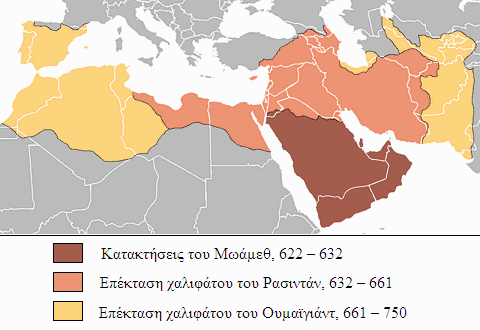
Η ανάπτυξη αυτή οφείλεται, σύμφωνα με μελετητές, στο οτι πολλοί Μουσουλμάνοι λόγιοι εστίασαν στον ανθρωπισμό και στη λογική και επιστημονική μελέτη, ενώ ήσαν ανοιχτοί στην ελευθερία του πνεύματος και στο σκεπτικισμό, δίνοντας έμφαση στο άτομο και όχι στους θεσμούς και στην εξουσία. Αυτά τα χαρακτηριστικά δυστυχώς εξαφανίστηκαν αργότερα, μετά από την παρακμή του Ισλαμικού κόσμου. Στο απόγειο του Ισλαμικού πολιτισμού, οι Μουσουλμάνοι λόγιοι έκαναν μεγάλο αριθμό μεταφράσεων Δυτικών κειμένων στα Αραβικά, και είναι μέσω των μεταφράσεων αυτών που τα αρχαία κείμενα (συμπεριλαμβανομένων και των Ελληνικών) διασώθηκαν και διαδόθηκαν αργότερα στην Ευρώπη. Πάντως καμιά θεμελιώδης επιστημονική ανακάλυψη δεν αποδίδεται στους Μουσουλμάνους αυτής της εποχής. Διέδωσαν τη χρήση του χαρτιού — γεγονός πολύ σημαντικό για τη μετέπειτα καταγραφή και διάδοση της γνώσης — αλλά τη μέθοδο κατασκευής του χαρτιού την έμαθαν (σύμφωνα με μια άποψη) από αιχμάλωτους Κινέζους, όταν νίκησαν τον Κινεζικό στρατό σε μια μάχη στο σημερινό Κιργιστάν. Το βέβαιο είναι οτι οι Κινέζοι γνώριζαν την κατασκευή και χρήση του χαρτιού από αιώνες πριν. Οι Μουσουλμάνοι επίσης παρέλαβαν από τους Ινδούς και διέδωσαν τη χρήση αυτών που σήμερα ονομάζουμε αραβικά ψηφία (0,1,2,3,4,5,6,7,8,9), και που χρησιμοποιούνται σχεδον παγκόσμια. Επίσης ανέπτυξαν την άλγεβρα, που αντικατέστησε τη γεωμετρία των αρχαίων Ελλήνων ως το κατ’ εξοχήν εργαλείο των μαθηματικών. Ίδρυσαν τα πρώτα πανεπιστήμια, και το αρχαιότερο εν λειτουργία πανεπιστήμιο βρίσκεται σήμερα στην πόλη Φεζ του Μαρόκου, και χρονολογείται από το 859 μ.Χ.
Αλχημεία
Η αλχημεία ήταν γνωστή σαν τέχνη από τους προχριστιανικούς χρόνους, και η ρίζα του ονόματος είναι ελληνική (από το χημία, που σημαίνει τη μετάλλαξη των μετάλλων, ενώ το αλ- είναι το αραβικό άρθρο). Ασχολήθηκαν μ’ αυτήν όχι μόνο στην Ευρώπη, αλλά και στην Ανατολή. Εικάζεται οτι πολλές πρακτικές ανακαλύψεις έχουν τη ρίζα-τους στις γνώσεις των αλχημιστών του Μεσαίωνα, χωρίς όμως αυτό να είναι επιβεβαιωμένο από έγκυρες μελέτες.

Πίνακας του Joseph Wright of
Derby (1734–1797):
«Ο αλχημιστής, ψάχνοντας για τη
φιλοσοφική λίθο, ανακαλύπτει τον φωσφόρο»
Η αλχημεία είχε το “θεωρητκό-της υπόβαθρο” στη θεωρία των τεσσάρων στοιχείων του Εμπεδοκλή (φωτιά, αέρας, νερό, γη). Εφόσον, σύμφωνα με τη θεωρία εκείνη, τίποτε το νέο δεν παράγεται στον κόσμο, αλλά καθετί που μας φαίνεται καινούριο προέρχεται από μια ανακατανομή των τεσσάρων στοιχείων στο “νέο” υλικό, έπεται οτι και ένα υλικό όπως ο χρυσός θα μπορούσε να παραχθεί μέσω μιας ανακατανομής των τεσσάρων στοιχείων. Εκτός από χρυσό, οι αλχημιστές συχνά προσπαθούσαν να φτιάξουν φάρμακα που να γιατρεύουν κάθε ασθένεια ή που να επαναφέρουν τη νεότητα. Επίσης στόχος-τους ήταν η λεγόμενη “φιλοσοφική λίθος”, που υποτίθεται οτι χάριζε την αθανασία στον κάτοχό της.
Γνώση μετάλλων και μεταλλουργίας μέχρι και το Μεσαίωνα
Η γνώση της εξόρυξης μετάλλων και της χρήσης-τους έπαιξε σπουδαίο ρόλο στην ανάπτυξη της επιστήμης διαχρονικά, γιατί με τα μέταλλα κατασκευάζονται ανθεκτικά εργαλεία, κατάλληλα για πειράματα που απαιτούν ακρίβεια.
Από την αρχαιότητα (προ Χριστού εποχή) ήσαν γνωστά τα εξής μέταλλα: χαλκός, χρυσός, άργυρος, κασσίτερος, σίδηρος, υδράργυρος, μόλυβδος, και ψευδάργυρος (ο τελευταίος ήταν άγνωστος σε καθαρή μορφή). Επίσης ήσαν γνωστά και τα αμέταλλα άνθρακας και θείο, καθώς βρίσκονται ελεύθερα στη φύση. (Βεβαίως κανένα από αυτά δεν αναγνωριζόταν σαν απλό χημικό στοιχείο, έννοια που θα έπαιρνε αρκετούς αιώνες για να εμφανιστεί.) Από τα μέταλλα, μόνο ο σίδηρος και κράματα χαλκού είναι κατάλληλα για κατασκευή εργαλείων. Με τον ψευδάργυρο και το χαλκό κατασκευάζεται ο ορείχαλκος, ενώ από χαλκό και κασσίτερο γίνεται ο μπρούντζος. Πέρα από αυτά, άλλα μέταλλα (στοιχειώδη ή κράματα) δεν ήσαν γνωστά στην αρχαιότητα. Μέχρι επομένως την προ Χριστού εποχή ήσαν γνωστά ακριβώς 9 στοιχεία (ή 10 αν συμπεριλάβουμε και τον ψευδάργυρο). Ενδιαφέρον παρουσιάζει οτι κατά τους επόμενους 15 αιώνες δεν απομονώθηκε από τη φύση παρά μόνο ένα επιπλέον στοιχείο, κι αυτό όχι ακριβώς μέταλλο (το αρσενικό, το 1250 μ.Χ.). Όλα τα υπόλοιπα φυσικά στοιχεία (περί τα 80) ανακαλύφθηκαν και απομονώθηκαν από το 15ο αιώνα και μετά.
Κατά τη Μεσαιωνική Εποχή της Ευρώπης όχι μόνο δεν ανακαλύφθηκαν νέα μέταλλα, αλλά ξεχάστηκε κ’ η τεχνογνωσία της εξόρυξης μετάλλων από τις ενώσεις-τους (δηλ. από τα πετρώματα που τα εμπεριέχουν), με αποτέλεσμα τα μεταλλικά αντικείμενα ν’ αρχίσουν να σπανίζουν. Η σιδερένια τσάπα κ’ η αξίνα έγιναν είδη πολυτελείας, ενώ το υνί για το όργωμα ήταν συχνά ξύλινο. Έτσι, κατά το Μεσαίωνα εξέλιπε όχι μόνο το ενδιαφέρον για τη μελέτη του φυσικού κόσμου (αφού αντί να μελετούν τη φύση οι λόγιοι μελετούσαν τις Γραφές), αλλά και η υλικοτεχνική υποδομή που θα υποβοηθούσε στη μελέτη αυτή. Χρειάστηκε να έρθουν οι πρώτοι αιώνες της Αναγέννησης (από το 15ο και μετά) για να επανεμφανιστούν τα μέταλλα και να κατασκευαστούν ανθεκτικά επιστημονικά εργαλεία.
Η αυγή της Αναγέννησης
Ενώ σε άλλα μέρη του κόσμου οι πολιτισμοί προχωρούσαν με βήμα σημειωτόν (π.χ. Κίνα), ή παρήκμαζαν και οπισθοδρομούσαν (π.χ. Ισλαμικός κόσμος, Βυζάντιο), στη Δυτική Ευρώπη άρχισαν να εμφανίζονται τα πρώτα σημάδια προόδου από το 15ο αιώνα. Όταν στα μέσα του 16ου αιώνα ο Κοπέρνικος πρότεινε το ηλιοκεντρικό σύστημα, δόθηκε ουσιαστικά το έναυσμα για μια αναθεώρηση δοξασιών που είχαν επικρατήσει απαράλλαχτες και χωρίς αμφισβήτηση για πάνω από μιάμιση χιλιετία.
Νικόλαος Κοπέρνικος (1473 – 1543)
Ο Πολωνός αστρονόμος και ιερέας Mikołaj Kopernik (Νικόλαος Κοπέρνικος), που η μητρική-του γλώσσα ήταν μάλλον τα Γερμανικά και όχι τα Πολωνικά, γεννήθηκε στο Τορούν της Πρωσσίας, που ήταν τότε μέρος του Βασιλείου της Πολωνίας. Το επώνυμό του προέρχεται από ένα χωριό της Σιλεσίας, το Kopernik, ή Köppernig, ή (σήμερα) Koperniki, απ’ όπου ήταν η καταγωγή της οικογένειάς του, και το πρόθεμα koper- ή köpper- πρέπει να σχετίζεται με την παραγωγή χαλκού (αγγλ.: copper) που γινόταν στην περιοχή εκείνη. Άλλωστε ο πατέρας-του ήταν έμπορος χαλκού.
 |
Ο Κοπέρνικος, που υπέγραφε το όνομά του άλλοτε ως Copernik, άλλοτε ως Kopperlingk, άλλοτε ως Coppernicus, κι άλλοτε ως N Copernic, σπούδασε αστρονομία και μαθηματικά αρχικά στην ακαδημία της Κρακοβίας, και αργότερα νομική στη Μπολόνια της Ιταλίας, με τα λεφτά του πλούσιου θείου-του, που κατείχε υψηλή θέση (“πρίγκηψ–επίσκοπος”) στην κοινωνία της χώρας-του. Ήταν μάλλον τα τέσσερα χρόνια στην Κρακοβία που του έδωσαν ένα γερό επιστημονικό υπόβαθρο. Μελέτησε τους αρχαίους Έλληνες φιλοσόφους, έμαθε ελληνικά, λατινικά, και αργότερα ιταλικά. Έτσι έκανε κτήμα-του την αντίφαση του Αριστοτέλειου συστήματος, που ήθελε τους πλανήτες, τον Ήλιο, και τη Σελήνη να περιφέρονται σε κύκλους (σφαίρες) γύρω από τη Γη, με το Πτολεμαϊκό σύστημα, που ήθελε τους πλανήτες να κινούνται σε επικυκλοειδείς τροχιές (βλ. μάθημα Ε1) γύρω από τη Γη. Τελειώνοντας τις σπουδές-του, ο Κοπέρνικος επέστρεψε στην Πολωνία, στην πόλη Φρόμπορκ (γερμανικά: Frauenburg), όπου αγόρασε έναν πυργίσκο, τον οποίο χρησιμοποίησε σαν αστρονομικό παρατηρητήριο, αλλά και κατοικία. |
Προς το τέλος της ζωής-του έγραψε τις απόψεις-του περί κίνησης των ουρανίων σωμάτων σ’ ένα βιβλίο, το “De revolutionibus orbium coelestium”, το οποίο δεν ήταν βέβαιος οτι ήθελε να εκδώσει. Τελικά πείσθηκε να το στείλει προς έκδοση μέσω ενός φίλου-του, και λέγεται οτι παρέλαβε το πρώτο τυπωμένο αντίτυπο όταν ήταν πια ετοιμοθάνατος.
 |
Στο εξώφυλλο του βιβλίου, που φαίνεται στην ανατύπωση αριστερά, διακρίνεται η ελληνική φράση: «ἀγεωμέτρητος οὐδεὶς ἐσίτω» (παραλλαγή της Πλατωνικής επιγραφής πάνω από την είσοδο της αρχαίας Ακαδημίας)· όπως και η χρονολογία έκδοσης: M.D.XLIII = 1543. Το De Revolutionibus χωρίζεται σε έξι “βιβλία” (ή κεφάλαια), ως εξής:
Στο αρχικό χειρόγραφο του βιβλίου, το οποίο διασώζεται, ο Κοπέρνικος αναφέρει οτι ήταν γνώστης των απόψεων περί ηλιοκεντρισμού των αρχαίων Ελλήνων (Φιλολάου, Αριστάρχου, και Ικέτα). Το σημείο όμως αυτό αφαιρέθηκε από το κείμενο που δόθηκε προς έκδοση, από τον φίλο του Κοπέρνικου Tiedemann Giese. Ξαναπροστέθηκε αργότερα, σε μεταγενέστερες εκδόσεις, όταν το ηλιοκεντρικό σύστημα είχε πια πάρει και την ονομασία “Κοπερνίκειο”. |
Πάντως, προς υπεράσπιση του Κοπέρνικου, πρέπει να τονιστεί οτι η συνεισφορά-του δεν είναι ταυτόσημη με αυτή του Αρίσταρχου του Σάμιου. Ο Αρίσταρχος έκανε απλώς την υπόθεση οτι η Γη και οι άλλοι πλανήτες περιφέρονται γύρω από τον Ήλιο, ενώ ο Κοπέρνικος χρησιμοποίησε μαθηματικούς (τριγωνομετρικούς) τύπους και τα δεδομένα από αστρονομικές παρατηρήσεις που ήσαν γνωστές στην εποχή-του (και από άλλες που έκανε ο ίδιος), δίνοντας έτσι ποσοτική μορφή στην ηλιοκεντρική θεωρία, ενώ η θεωρία του Αρίσταρχου ήταν — απ’ όσο γνωρίζουμε μέσω του Αρχιμήδη — ποιοτικής μορφής. Η ποσοτική διατύπωση μιας θεωρίας είναι σημαντικότατη, γιατί μέσω αυτής μπορούμε να κάνουμε προβλέψεις, που είναι ένα θεμελιώδες χαρακτηριστικό μιας επιστημονικής θεωρίας, αφού αν οι προβλέψεις δεν επαληθευτούν από τις μελλοντικές παρατηρήσεις, τότε η θεωρία διαψεύδεται και απορρίπτεται.
Το De Revolutionibus θεωρήθηκε επαναστατικό για την εποχή εκείνη. Μάλιστα στις γλώσσες με λατινική προέλευση ή επιρροές, η λέξη “περιφορά” (π.χ., αγγλ./γαλλ.: revolution) απέκτησε και την έννοια “επανάσταση”. Το βιβλίο δεν ξεσήκωσε αμέσως κάποιο κύμα αντίδρασης από την Ρωμαιοκαθολική Εκκλησία (της οποίας άλλωστε ο Κοπέρνικος ήταν επίσκοπος). Η αντίδραση ήρθε αργότερα, την εποχή του Γαλιλαίου, που έδρασε στην Ιταλία περίπου μισό αιώνα μετά το θάνατο του Κοπέρνικου.
Η αυγή της νεώτερης φάσης της επιστήμης
Όπως τονίστηκε στο μάθημα Ε1, η επιστήμη με τη σημερινή έννοια στηρίζεται στην επιστημονική μέθοδο, και αυτή με τη σειρά-της περιλαμβάνει ορισμένα “βήματα” (αποτυπωμένα στο λογότυπο του Δ.Ε.Π.), τα πρώτα από τα οποία είναι η παρατήρηση και το πείραμα. Κατά το 16ο αιώνα άρχισαν να εμφανίζονται με μεγαλύτερη συχνότητα ερευνητές της φύσης που δεν δέχονταν ασυζητητί το κύρος της αυθεντίας προκειμένου να δεχτούν κάτι σαν σωστό, αλλά έκαναν παρατηρήσεις, θέλοντας να βεβαιωθούν με τα ίδια-τους τα μάτια. Ένας από τους ανθρώπους αυτούς ήταν ο Γαλιλαίος, που από πολλούς θεωρείται ο “πατέρας της σύγχρονης επιστήμης”.
Γαλιλαίος (Galileo Galilei, 1564 – 1642)
 |
Ο Γαλιλαίος γεννήθηκε στην Πίζα, στο Δουκάτο της Φλωρεντίας. (Δεν υπήρχε ακόμα το κράτος της Ιταλίας.) Ξεκίνησε τις σπουδές-του με την ιατρική, γρήγορα όμως τον τράβηξαν τα μαθηματικά, οπότε αφοσιώθηκε στη μελέτη των μαθηματικών και της “φυσικής φιλοσοφίας” όπως λεγόταν τότε η μελέτη της φυσικής, της αστρονομίας, αλλά και της αστρολογίας, που δεν είχε γίνει ακόμη κατανοητή σαν ένα σύνολο αντιλήψεων στερούμενων κάθε επιστημονικής βάσης. Το στοιχείο το οποίο συσχετίζουμε πιο έντονα με τη μορφή του Γαλιλαίου είναι οτι με μια σειρά παρατηρήσεων και πειραμάτων κατέδειξε οτι ένας αριθμός αρχαίων αντιλήψεων (θα δούμε στη συνέχεια ποιες) ήσαν λαθεμένες. Έτσι, ήρθε σιγά-σιγά σε σύγκρουση με την Καθολική Εκκλησία, γιατί η τελευταία είχε ορισμένα παγιωμένα δόγματα για το πώς υποτίθεται οτι είναι πλασμένος ο κόσμος, που ήσαν απόρροια των Γραφών και των αρχαίων φιλοσοφικών αντιλήψεων του Πλάτωνα και κυρίως του Αριστοτέλη, οι οποίες βρίσκονταν σε σύμπνοια με τις Χριστιανικές Γραφές. Ο Γαλιλαίος υποστήριξε το ηλιοκεντρικό σύστημα του Κοπέρνικου, στο οποίο είχε ήδη εναντιωθεί η Εκκλησία. Τα τελευταία χρόνια της ζωής-του υποχρεώθηκε να τα περάσει σε κατ’ οίκον περιορισμό. |
Ο Γαλιλαίος είχε έφεση στο να φτιάχνει χρήσιμες συσκευές, ήταν δηλαδή και εφευρέτης. Έτσι, ακούγοντας απλώς την περιγραφή του τηλεσκοπίου (που δεν είχε τότε ακόμη όνομα) από έναν Ολλανδό που είχε κατασκευάσει ένα, σκάρωσε το δικό-του, που του έδινε εικόνα τρεις φορές μεγαλύτερη από την πραγματική, και “ορθή” (δηλαδή μη ανεστραμμένη). Επειδή η εικόνα ήταν ορθή, η συσκευή κίνησε το ενδιαφέρον των θαλασσοπόρων εμπόρων, που μπορούσαν τόσο να χρησιμοποιούν το τηλεσκόπιο στη θαλασσοπλοΐα, όσο και να το πουλούν στα μέρη που ταξίδευαν. Ο Γαλιλαίος όμως δεν ενδιαφερόταν τόσο για το εμπόριο, όσο γι’ αυτά που έβλεπε όταν έστρεφε το τηλεσκόπιό του στον ουρανό.
Αυτά που έβλεπε τον εντυπωσίαζαν πολύ. Κατ’ αρχήν, στις 7 Ιανουαρίου του 1610 παρατήρησε πολύ κοντά στο Δία «τρεις απλανείς αστέρες, εντελώς αόρατους [με γυμνό μάτι] λόγω του μικρού μεγέθους-τους», που κείτονταν σε μια ευθεία με τον πλανήτη. Τις επόμενες ημέρες, με έκπληξη διαπίστωσε οτι οι υποτιθέμενοι “απλανείς” αστέρες άλλαζαν θέση στον ουρανό, παραμένοντας όμως πάντα πολύ κοντά στο Δία, και πάντα σε μια ευθεία γραμμή. Στις 10 Ιανουαρίου διαπίστωσε οτι το ένα αστεράκι εξαφανίστηκε, πράγμα που τον έκανε να συμπεράνει οτι κρύφτηκε πίσω από το Δία. Στις 13 Ιανουαρίου ανακάλυψε και τον τέταρτο από αυτούς που σήμερα ονομάζουμε “Γαλιλαιικούς δορυφόρους” του Δία, δηλαδή τους τέσσερις μεγαλύτερους, και σύντομα συμπέρανε οτι οι αστέρες αυτοί περιφέρονταν γύρω από τον πλανήτη. Αυτό το συμπέρασμα ερχόταν σε σύγκρουση με την επικρατούσα Πτολεμαϊκή άποψη οτι όλα τα ουράνια σώματα κινούνται σε σφαίρες με κέντρο τη Γη, αφού ξαφνικά ανακαλύφθηκε ένα άλλο κέντρο: ο Δίας.
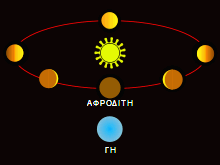
Ακόμα πιο ανατρεπτική για τις επικρατούσες αντιλήψεις ήταν η παρατήρησή του οτι η Αφροδίτη παρουσιάζει φάσεις, ακριβώς όπως το φεγγάρι (βλ. διάγραμμα, παραπάνω). Οι φάσεις της Αφροδίτης δεν μπορούσαν να εξηγηθούν παρά μόνο αν ο πλανήτης περιφερόταν γύρω από τον Ήλιο. Αντίθετα, το γεωκεντρικό σύστημα των Αριστοτέλη–Πτολεμαίου ήθελε, όπως είπαμε, κέντρο όλων των τροχιών να είναι η Γη. Αν όμως η φαινόμενη κίνηση της Αφροδίτης στον ουρανό μπορούσε να εξηγηθεί σαν περιφορά γύρω από τον Ήλιο, τότε το ίδιο έπρεπε να συμβαίνει και με τον Ερμή, που είχε φαινόμενη τροχιά με ιδιότητες παρόμοιες με εκείνες της τροχιάς της Αφροδίτης — κι ας μην είχε το τηλεσκόπιο του Γαλιλαίου τη δύναμη να του δείξει τις φάσεις του Ερμή.
Τις παρατηρήσεις περί Αφροδίτης ο Γαλιλαίος τις έκανε το Σεπτέμβριο του 1610. Εντωμεταξύ είχε ήδη παρατηρήσει τις κηλίδες στον Ήλιο και την κίνησή τους πάνω σ’ αυτόν (δεν έδωσε όμως τη σωστή ερμηνεία οτι ο Ήλιος περιστρέφεται)· τα βουνά της Σελήνης, που έδειχναν μια επιφάνεια ανάγλυφη σαν της Γης (αντίθετα με την Αριστοτέλεια άποψη της τέλειας Σεληνιακής σφαίρας)· και το οτι ο “Γαλαξίας” αποτελείται από εκατομμύρια διακριτά άστρα, που λόγω της πολύ μεγάλης απόστασής τους δεν μπορούμε να τα δούμε ξεχωριστά. Συμπέρανε, σωστά, οτι κάθε άστρο είναι σαν ένας Ήλιος.
Το 1616 ο Γαλιλαίος ταξίδεψε στη Ρώμη, προσπαθώντας να πείσει την Εκκλησία να μην εναντιωθεί στις απόψεις-του. Εντωμεταξύ όμως η αντίθεση στο ηλιοκεντρικό σύστημα είχε φτάσει στο κατακόρυφο. Η αντίθεση αυτή οφειλόταν σε έναν αριθμό φράσεων της Παλαιάς Διαθήκης, όπως π.χ. οτι «Ο Κύριος [...] την οικουμένην εστερέωσεν ώστε δεν θέλει σαλευθεί» (Ψαλ. 93:1 και 96:10, Χρον. 16:30), οτι «ο θεμελιών την γην επί την βάσιν αυτής, ίνα μη σαλευθή εις τον αιώνα του αιώνος» (Ψαλ. 104:5), ή οτι «Και ανατέλλει ο Ήλιος, και δύει ο Ήλιος, και σπεύδει προς τον τόπον αυτού όθεν ανέτειλεν» (Εκκλ. 1:5). Ας σημειωθεί οτι η Αγία Γραφή εκείνο τον καιρό εκλαμβανόταν κατά κυριολεξία, σαν ο αυτούσιος και αμετάκλητος λόγος του Θεού. Το ταξίδι του Γαλιλαίου είχε το αντίθετο αποτέλεσμα, όταν ο καρδινάλιος Bellarmine, ακολουθώντας οδηγίες της Ιεράς Εξέτασης, τον υποχρέωσε να μην υποστηρίζει πλέον το ηλιοκεντρικό σύστημα. Πάντως ο Γαλιλαίος συνέχισε να συζητεί τις ιδέες-του, χωρίς όμως να έρχεται σε ανοιχτή σύγκρουση με την Εκκλησία.
Το 1623, Πάπας έγινε ο Ουρβανός ο 8ος, που ήταν προσωπικός γνωστός του Γαλιλαίου. Έτσι ο τελευταίος ενθαρρύνθηκε να γράψει ένα βιβλίο, το «Διάλογος περί των δύο κύριων συστημάτων του κόσμου», που εκδόθηκε το έτος 1632, και ουσιαστικά προέκρινε το ηλιοκεντρικό σύστημα σαν το σωστό. Μάλιστα ο ίδιος ο Ουρβανός παρώτρυνε τον Γαλιλαίο να καταγράψει τα επιχειρήματα, τόσο τα κατά όσο και τα υπέρ του ηλιοκεντρικού συστήματος, αλλά και να συμπεριλάβει τις απόψεις του Πάπα σ’ αυτό. Ατυχώς, ο Γαλιλαίος συμπεριέλαβε μεν τις απόψεις του Ουρβανού, αλλά τις έβαλε στο στόμα του χαρακτήρα του βιβλίου Σιμπλίσιου (Simplicio), που στα Ιταλικά έχει επίσης και την έννοια του “απλοϊκός”. Και πράγματι, ο Simplicio μ’ αυτά που υποστήριζε στο βιβλίο δεν εμφανιζόταν ιδιαίτερα έξυπνος. Αυτό έκανε τον Πάπα να εξοργιστεί και να γίνει εχθρός του Γαλιλαίου. Έτσι, το 1633 ο Γαλιλαίος κλήθηκε στη Ρώμη για να δικαστεί ως ύποπτος αίρεσης. Πράγματι, δικάστηκε και καταδικάστηκε με ποινή φυλάκισης, που αργότερα μετατράπηκε σε κατ’ οίκον περιορισμό. Επίσης διατάχθηκε να «αποταχθεί, καταραστεί, και αναθεματίσει» τις απόψεις-του. Σύμφωνα με ένα μύθο, αφού ο Γαλιλαίος δήλωσε επίσημα οτι η Γη είναι ακίνητη, ψιθύρισε χωρίς να τον ακούσουν οι δικαστές: «Και όμως, γυρίζει» (Ιταλ.: «E pur si muove»)· δεν υπάρχει όμως καμιά ένδειξη οτι αυτός ο μύθος έχει βάση στην πραγματικότητα, καθώς αναφέρεται για πρώτη φορά έναν αιώνα μετά το θάνατό του. Σίγουρα ο Γαλιλαίος δεν ήθελε να έχει την τύχη του φιλοσόφου Τζιορντάνο Μπρούνο (Giordano Bruno), που το 1600 κάηκε στην πυρά από την Ιερά Εξέταση, επειδή υποστήριζε οτι ούτε καν ο Ήλιος είναι ακίνητος, αλλά οτι τόσο ο Ήλιος όσο και τα άστρα (που είναι άλλοι Ήλιοι) βρίσκονται σε αέναη κίνηση, και οτι το σύμπαν είναι άπειρο.
Αν όμως ο Γαλιλαίος ήταν γνωστός μόνο σαν υποστηρικτής του ηλιοκεντρικού συστήματος, δεν θα θεωρούνταν σαν μια από τις πιο σημαντικές φυσιογνωμίες στην ιστορία της επιστήμης. Έβαλε επίσης και τα θεμέλια της φυσικής, καθώς διατύπωσε αυτό που αργότερα έγινε γνωστό σαν “1ος νόμος του Νεύτωνα”· οτι δηλαδή αν σε ένα σώμα δεν ασκείται καμία δύναμη, αυτό τείνει να συνεχίσει να κινείται σε ευθεία γραμμή με σταθερή ταχύτητα — εφόσον δεν υπάρχει τριβή ή αντίσταση του αέρα. (Αντίθετα, η άποψη του Αριστοτέλη ήταν οτι τα κινούμενα σώματα σταματούν μετά από λίγο — άποψη που είναι σύμφωνη με την καθημερινή εμπειρία, αλλά λανθασμένη ως προς τη φυσική πραγματικότητα.) Ο Γαλιλαίος, όσο ήταν σε κατ’ οίκον περιορισμό, έγραψε το βιβλίο “Δύο νέες επιστήμες”, που πραγματεύεται την κίνηση των σωμάτων και την αντοχή των υλικών, και που αποτέλεσε θεμελιακή αναφορά στον νεοαναπτυσσόμενο τομέα της φυσικής. Πέθανε το 1642 στο σπίτι-του, έχοντας χάσει εντελώς την όρασή του, πιθανώς λόγω των παρατηρήσεων του Ήλιου που έκανε χωρίς προφυλάξεις.
Με τον Γαλιλαίο παρατηρούμε την εκκίνηση μιας διαδικασίας “τριβής” της επιστήμης με τη θρησκεία, που συνεχίζεται (αλλά με πολύ μειωμένη ένταση) ως τις μέρες-μας. Η τριβή οφείλεται στο οτι η θρησκεία (όχι μόνο ο Χριστιανισμός, αλλά η κάθε θρησκεία) έχει αρχές που βρίσκονται σε σύγκρουση με τις επιστημονικές. Συγκεκριμένα, για να ανακαλύψει την αλήθεια η θρησκεία εξετάζει όχι την πραγματικότητα (τον φυσικό κόσμο), αλλά τα ιερά-της κείμενα που συνήθως έχουν γραφεί πολλούς αιώνες πριν, και την “αλήθεια” αυτή την εκλαμβάνει ως απόλυτη. Αντίθετα, η επιστήμη κάνει παρατηρήσεις επί του φυσικού κόσμου για να βρει ποιο είναι το σωστό, και όταν οι παρατηρήσεις διαφωνούν με την “αλήθεια” (τη θεωρία), τότε απορρίπτεται η θεωρία, όχι οι παρατηρήσεις. Αυτή είναι και η ουσία της “τριβής” του Γαλιλαίου με την Καθολική Εκκλησία, αφού οι παρατηρήσεις-του κατέρριπταν την παραδεκτή “αλήθεια”. Από τότε μέχρι σήμερα η ιστορία περιγράφει μια σειρά από συμβιβασμούς της Εκκλησίας, ώστε οι απόψεις-της να μη συγκρούονται με τις επιστημονικές παρατηρήσεις.
Johannes Kepler (Γιοχάννες Κέπλερ, 1571 – 1630)
Ο Γερμανός μαθηματικός, αστρονόμος, και αστρολόγος Johannes Kepler
 |
Γεννημένος πρόωρα, ήταν ασθενικός σαν παιδί, και όταν πέρασε την ανεμοβλογιά έχασε ένα μέρος της οξύτητας της όρασής του και της επιδεξιότητας των χεριών-του, πράγμα που τον εμπόδισε αργότερα στις αστρονομικές-του παρατηρήσεις. Όταν ήταν έξι χρονών είδε το Μεγάλο Κομήτη του 1577, αυτόν που παρατήρησε ο Δανός αστρονόμος Τύχο Μπράχε (που όπως θα δούμε έπαιξε ρόλο στη ζωή του Κέπλερ· ο κομήτης αυτός πιστεύεται οτι σήμερα βρίσκεται σε απόσταση περίπου ίση με 300 φορές την απόσταση Γης-Ηλίου). Επίσης όταν ήταν εννέα χρονών παρατήρησε μια έκλειψη Σελήνης. Αυτά τα γεγονότα του έκαναν μεγάλη εντύπωση, και ίσως να δρομολόγησαν το μέλλον-του. Πάντως ο Κέπλερ είχε από μικρός μεγάλη έφεση και ικανότητες στα μαθηματικά. Ξεκίνησε τις σπουδές-του στο πανεπιστήμιο του Tübingen σαν φοιτητής της θεολογίας, όπου σπούδασε φιλοσοφία, μαθηματικά, και διακρίθηκε στην κατασκευή αστρολογικών ωροσκόπων για τους συμφοιτητές-του. Αυτή η ενασχόλησή του με την αστρολογία επρόκειτο να συνεχιστεί και αργότερα. |
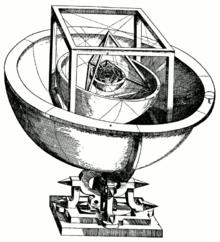
Η πρώτη-του αστρονομική εργασία, το “Mysterium Cosmographicum” («Κοσμογραφικό μυστήριο») ήταν ένα μείγμα επιστημονικών παρατηρήσεων και “ευσεβών πόθων”. Συγκεκριμένα, ο Κέπλερ θεώρησε οτι μεταξύ των τροχιών των έξι τότε γνωστών πλανητών (Ερμή, Αφροδίτης, Γης, Άρη, Δία, και Κρόνου), μπορούσαν να παρεμβληθούν τα πέντε Πλατωνικά πολύεδρα (οκτάεδρο, εικοσάεδρο, δωδεκάεδρο, τετράεδρο, και κύβος, μ’ αυτή τη σειρά — βλέπε σχήμα).
 |
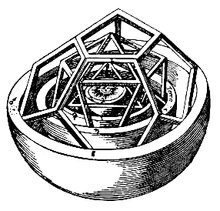 |
| Το εξωτερικό του μοντέλου του ηλιακού συστήματος σύμφωνα με τον Κέπλερ: κύβος εγγεγραμμένος μεταξύ των τροχιών Κρόνου και Δία, και τετράεδρο μεταξύ των τροχιών Δία και Άρη. | Πιο εσωτερικά, το μοντέλο του Κέπλερ περιλάμβανε δωδεκάεδρο μεταξύ των τροχιών Άρη και Γης, εικοσάεδρο μεταξύ Γης και Αφροδίτης, και ένα οκτάεδρο μεταξύ Αφροδίτης και Ερμή. |
Φυσικά, αυτά τα πολύεδρα που φαντάστηκε ο Κέπλερ καμία σχέση δεν είχαν με την πραγματικότητα, και μάλιστα το ταίριασμά-τους ήταν δυνατό μόνο λόγω των ελλιπών δεδομένων που διέθετε ο Κέπλερ. Εκείνος όμως θεώρησε οτι κατάφερε να δει ένα μέρος από το πλάνο του Θεού για το σύμπαν. Πιο σημαντικό ήταν οτι το μοντέλο-του προϋπέθετε το ηλιοκεντρικό σύστημα του Κοπέρνικου, που είχε ήδη αρχίσει να σηκώνει θύελλα αντίδρασης, κυρίως από τη μεριά της Εκκλησίας. Ο Κέπλερ πάντως ήταν προστατευόμενος του αυτοκράτορα Ροδόλφου του Β΄, ως προσωπικός-του αστρολόγος, και γιαυτό δεν κινδύνεψε ιδιαίτερα.
|
Χρειαζόταν όμως μεγαλύτερη ακρίβεια παρατηρήσεων για την εγκυρότητα του πλανητικού-του μοντέλου, και ο ίδιος δεν μπορούσε να κάνει πιο ακριβείς παρατηρήσεις με τα μέσα που διέθετε. Έτσι ήρθε σε επαφή με το Δανό αστρονόμο Τύχο Μπράχε, στον οποίο έστειλε ένα αντίγραφο του έργου-του. Ο Τύχο τον προσκάλεσε στην Πράγα όπου εργαζόταν στο παρατηρητήριό του, και ο Κέπλερ τον επισκέφτηκε εκεί τον Φεβρουάριο του 1600. Στην αρχή ο Τύχο δεν ήθελε να του αποκαλύψει τα λεπτομερή δεδομένα των παρατηρήσεών του. Σιγά-σιγά όμως εμπιστεύθηκε τον Κέπλερ, και τελικά ήρθαν σε μια συμφωνία όπου ο Κέπλερ προσλήφθηκε από τον Τύχο για να εργαστεί στο παρατηρητήριο. Τον Οκτώβριο του 1601 όμως ο Τύχο πέθανε αιφνίδια, και ο Κέπλερ διορίστηκε διάδοχός του στο παρατηρητήριο. Έτσι τα πλήρη δεδομένα του Τύχο έγιναν προσβάσιμα στον Κέπλερ, για τον οποίο τα επόμενα 11 χρόνια υπήρξαν τα πιο παραγωγικά της ζωής-του. Με τα δεδομένα του Τύχο, ο Κέπλερ κατάλαβε οτι το μοντέλο-του με τα εγγεγραμμένα κανονικά πολύεδρα δεν μπορούσε να είναι σωστό. Έτσι άρχισε να εξετάζει την περίπτωση οι τροχιές των πλανητών να μην είναι κύκλοι, όπως ήταν γενικά παραδεκτό μέχρι τότε, αλλά να είχαν το σχήμα... αυγού! (Δηλαδή μιας έλλειψης πιο μυτερής στο ένα άκρο.) Την περίπτωση του να είναι απλώς ελλείψεις, αρχικά δεν τη θεώρησε άξια προσοχής. |
|
Τελικά, μετά από πολλές προσπάθειες, και αφού τα δεδομένα δεν ταίριαζαν σε καμία άλλη υπόθεση, κατέληξε στο συμπέρασμα οτι οι πλανητικές τροχιές είναι ελλείψεις που έχουν τον Ήλιο στη μια από τις δυο “εστίες” της έλλειψης (βλ. σχήμα που ακολουθεί).
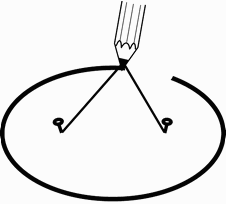
Κατασκευή έλλειψης από τις δύο εστίες-της
Το παραπάνω σχήμα δείχνει πώς μπορούμε να κατασκευάσουμε μια έλλειψη από τις δύο εστίες-της: καρφώνουμε από ένα καρφί σε κάθε μία από τις δύο εστίες (που επιλέγουμε αυθαίρετα σαν δυο σημεία στο επίπεδο) και δένουμε ένα χαλαρό σπάγγο στις δύο εστίες. Τεντώνουμε το σπάγγο με ένα μολύβι, όπως στο σχήμα, και καθώς κινούμε το μολύβι, αυτό διαγράφει μια έλλειψη, περιοριζόμενο από το σπάγγο. Σε ένα πλανητικό σύστημα, ο ήλιος βρίσκεται στη μια από τις δυο εστίες, και ο πλανήτης κινείται πάνω στην έλλειψη.
Στην πραγματικότητα όμως, οι τροχιές των πλανητών του συστήματός μας, ενώ είναι ελλείψεις, μοιάζουν πάρα πολύ με κύκλους (και οι εστίες-τους είναι πολύ κοντά η μία στην άλλη). Το παρακάτω διάγραμμα δείχνει τις πραγματικές τροχιές των τεσσάρων “γήινων” πλανητών (Ερμή, Αφροδίτης, Γης, και Άρη), στις σχετικές μεταξύ-τους αποστάσεις:
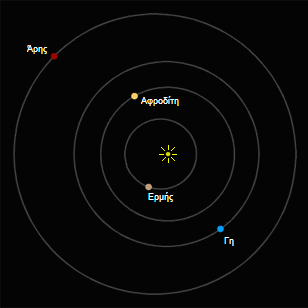
Με κλικ στην εικόνα μεταφέρεστε σε ιστοσελίδα που
δείχνει τους πλανήτες περιφερόμενους
γύρω από τον Ήλιο, με τις πραγματικές σχετικές μεταξύ-τους ταχύτητες
περιφοράς.
Βλέπουμε λοιπόν οτι παρόλο που πρόκειται για ελλείψεις, οι τροχιές των πλανητών που ήσαν γνωστοί την εποχή του Κέπλερ (συμπεριλαμβανομένων και των Δία και Κρόνου) είναι τόσο κοντά στο σχήμα του κύκλου που μόνο με τα λεπτομερειακά δεδομένα του Τύχο Μπράχε μπόρεσε ο Κέπλερ να αναγνωρίσει τη διαφορά, και να συμπεράνει οτι πρόκειται για ελλείψεις και όχι κύκλους.
Τελικά, αυτή η παρατήρηση έγινε γνωστή ως “1ος νόμος του Κέπλερ”:
| 1ος
νόμος του Κέπλερ: Η τροχιά κάθε πλανήτη είναι μια έλλειψη, με τον Ήλιο να βρίσκεται στη μια εστία της έλλειψης. |
Ο Κέπλερ διατύπωσε επίσης άλλους δύο νόμους που αφορούν στην κίνηση των πλανητών:
| 2ος
νόμος του Κέπλερ: Η γραμμή που ενώνει τον πλανήτη με τον Ήλιο σαρώνει ίσες επιφάνειες σε ίσους χρόνους. |
Το τί σημαίνει ο 2ος νόμος μας το δείχνει παραστατικά το σχήμα που ακολουθεί:

Όπως φαίνεται στο σχήμα, όλες οι κίτρινες και πορτοκαλί επιφάνειες υποτίθενται ίσες μεταξύ-τους σε εμβαδό. Ο πλανήτης διανύει το κυρτό μέρος της κάθε επιφάνειας στον ίδιο χρόνο. Για να συμβεί αυτό, προφανώς ο πλανήτης πρέπει να “τρέχει πιο γρήγορα” όταν είναι κοντά στον Ήλιο, αφού τότε η επιφάνεια είναι πιο “κοντή”, άρα για να γίνει ίση με τις άλλες (τις επιμήκεις) πρέπει να έχει πιο μεγάλη κυρτή πλευρά. Και πράγματι έτσι συμβαίνει, με τη διαφορά οτι επειδή οι πραγματικές τροχιές των πλανητών είναι σχεδόν σαν κύκλοι, οι διαφορές στην ταχύτητα του πλανήτη είναι ελάχιστες. Οι κομήτες όμως, που συνήθως έχουν πολύ ελλειπτικές τροχιές, παρουσιάζουν εμφανώς αυτή τη συμπεριφορά, δηλαδή επιταχύνουν πολύ καθώς πλησιάζουν τον Ήλιο, και επιβραδύνουν πολύ καθώς απομακρύνονται.
Ο τρίτος νόμος είναι λίγο πιο δύσκολος στην κατανόηση:
| 3ος
νόμος του Κέπλερ: Το τετράγωνο της περιόδου ενός πλανήτη είναι ανάλογο του κύβου του κύριου ημιάξονα της ελλειπτικής τροχιάς-του. |
Τί είναι ο “κύριος ημιάξονας”; Κάθε έλλειψη έχει ένα μέγιστο μήκος. Αυτό το μήκος είναι ο “κύριος άξονας” της έλλειψης. Το μισό του μήκους αυτού είναι ο “κύριος ημιάξονας”. Τώρα, ο 3ος νόμος του Κέπλερ λέει το εξής: ας πούμε οτι ο χρόνος μιας πλήρους περιφοράς του πλανήτη γύρω από τον Ήλιο είναι Τ (π.χ., για τη Γη: Τ = 1 έτος), και έστω R το μήκος του κύριου ημιάξονα. Τότε ισχύει οτι Τ2 = k·R3, όπου το k είναι μία σταθερά. Η φράση «είναι ανάλογο» σημαίνει «είναι πολλαπλάσιο επί μια σταθερά».
Το πρακτικό αποτέλεσμα του τρίτου νόμου είναι οτι όσο πιο κοντά στον Ήλιο είναι ο πλανήτης, τόσο πιο γρήγορα γυρίζει (δηλ. τόσο πιο μικρό είναι το “έτος” του πλανήτη). Π.χ., ο Ερμής, που είναι πιο κοντά στον ήλιο από όλους τους πλανήτες, συμπληρώνει μια πλήρη περιφορά σε 88 ημέρες (τόσο διαρκεί το “Ερμήειο έτος”)· το Γήινο έτος, όπως ξέρουμε, διαρκεί 365 ημέρες· το Αρειανό έτος 687 ημέρες· κ.ο.κ., ενώ το Ποσειδώνειο έτος διαρκεί περίπου 165 Γήινα έτη.
Φυσικά, οι παραπάνω νόμοι δεν ισχύουν μόνο για τους πλανήτες, αλλά και για τους δορυφόρους-τους, και για τους κομήτες, και γενικά για οποιοδήποτε ουράνιο σώμα περιφέρεται γύρω από ένα άλλο που έχει πολύ μεγαλύτερη μάζα. Αυτή λοιπόν είναι η μεγάλη συνεισφορά του Κέπλερ: οτι διατύπωσε τους νόμους που διέπουν την κίνηση των ουρανίων σωμάτων.
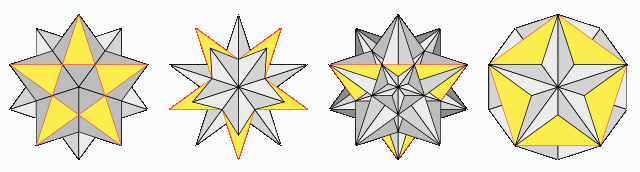
Έκανε όμως και άλλες ανακαλύψεις στη ζωή-του. Για παράδειγμα, κατασκεύασε έναν τύπο τηλεσκοπίου που έδινε καλύτερη ανάλυση από το τηλεσκόπιο του Γαλιλαίου, αλλά με την εικόνα ανεστραμμένη. Ο Γαλιλαίος όμως δεν υιοθέτησε το τηλεσκόπιο του Κέπλερ και συνέχισε να χρησιμοποιεί το δικό-του. Επίσης ο Κέπλερ περιέγραψε τα πολύεδρα που σήμερα είναι γνωστά ως “πολύεδρα Κέπλερ–Πουανσό” (Poinsot):
 |
|||
|
Μικρό αστεροειδές δωδεκάεδρο |
Μεγάλο αστεροειδές δωδεκάεδρο |
Μεγάλο |
Μεγάλο |
|
Τα πολύεδρα Κέπλερ – Πουανσό |
|||
Πρόκειται, κατά μία άποψη, για “κανονικά πολύεδρα”! Αντίθετα όμως με τα Πλατωνικά κανονικά πολύεδρα, τα πολύεδρα Κέπλερ–Πουανσό επιτρέπουν στις έδρες-τους να τέμνουν το πολύεδρο. Η έδρα των δύο πολυέδρων στ’ αριστερά είναι το πεντάκτινο αστέρι (γνωστό και ως “πεντάλφα”, κίτρινο χρώμα)· η έδρα του τρίτου είναι το ισόπλευρο τρίγωνο, και του τέταρτου το κανονικό πεντάγωνο.
René Descartes (Ρενέ Ντεκάρτ, ή Καρτέσιος, 1596 – 1650)
 |
Ο René Descartes Ο Ντεκάρτ γεννήθηκε στη Γαλλία, σε ένα μικρό χωριό που σήμερα φέρει το όνομά του προς τιμήν-του, αλλά έζησε τα πιο παραγωγικά χρόνια της ζωής-του στην Ολλανδία. Πολλές από τις πιο σημαντικές ιδέες-του του ήρθαν στο νου κατά τη διάρκεια ονείρων ή οραμάτων, όπως περιέγραψε ο ίδιος στα συγγράμματά του. Σαν φιλόσοφος υπήρξε υποστηρικτής του ορθολογιστικού κινήματος (αγγλ.: rationalism), που θεωρεί το λογικό σαν την πηγή της γνώσης, και αντιτίθεται στον εμπειρισμό, που θεωρεί οτι η γνώση προέρχεται από την εμπειρική εξέταση του κόσμου μέσω των αισθήσεων. |
Η συνεισφορά του Ντεκάρτ στα μαθηματικά είναι τόσο θεμελιακή που σήμερα ακόμη και οι μαθητές Γυμνασίου έρχονται σε επαφή με το έργο-του, όταν μαθαίνουν περί καρτεσιανού συστήματος συντεταγμένων (βλ. σχήμα).
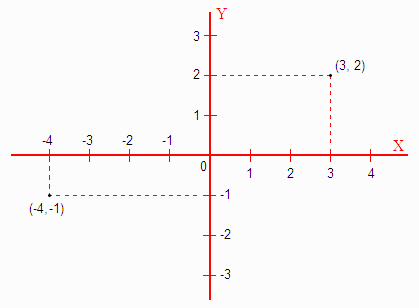
Καρτεσιανό σύστημα συντεταγμένων
Ένα καρτεσιανό σύστημα συντεταγμένων για το επίπεδο (που είναι ένας διδιάστατος χώρος) τοποθετεί δύο άξονες πάνω σ’ αυτό: έναν οριζόντιο που ονομάζεται “Χ”, και έναν κατακόρυφο που ονομάζεται “Υ”. (Στον τριδιάστατο χώρο έχουμε και τρίτο άξονα, τον άξονα “Ζ”.) Οι δύο άξονες Χ και Υ συνήθως είναι κάθετοι μεταξύ-τους, αν και αυτό δεν είναι απαραίτητο. Ο κάθε άξονας έχει διαβαθμίσεις επάνω-του, όπως η μεζούρα ή το μέτρο (το εργαλείο). Έτσι, κάθε “πραγματικός αριθμός” (δηλαδή όχι μόνο οι ακέραιοι, αλλά και οι δεκαδικοί, και οι αρνητικοί αριθμοί) αποτυπώνεται σε καθέναν από τους δύο άξονες. Με τον τρόπο αυτόν, κάθε σημείο του επιπέδου αποκτά ένα “όνομα”, δηλαδή μια ετικέττα. Π.χ., στο σχεδιάγραμμα φαίνονται τα σημεία (3, 2) και (–4, –1). Αυτή είναι και η βάση του “παντρέματος” της γεωμετρίας με την άλγεβρα, γιατί με τον παραπάνω τρόπο το κάθε γεωμετρικό σημείο αποκτά μια αλγεβρική παράσταση (π.χ.: (3, 2)). Δεν πρόκειται όμως για τα σημεία μόνο, αλλά για κάθε γεωμετρικό αντικείμενο. Π.χ., αν τραβήξουμε μια οποιαδήποτε ευθεία γραμμή στο επίπεδο, αυτή θα περιγράφεται από μια “πρωτοβάθμια εξίσωση” της μορφής αx + β = 0. Ένας κύκλος περιγράφεται από μια “δευτεροβάθμια εξίσωση”, κλπ. Οπότε είναι δυνατό να εξάγουμε γεωμετρικά συμπεράσματα μεταχειριζόμενοι αλγεβρικά αντικείμενα. Π.χ. είναι δυνατό να βρούμε σε ποια σημεία τέμνει μια ευθεία έναν κύκλο λύνοντας απλώς το σύστημα των δύο εξισώσεών τους — και η λύση συστημάτων εξισώσεων είναι ένα στοιχειώδες πρόβλημα άλγεβρας. Αυτή είναι και η ουσία της αναλυτικής γεωμετρίας: οτι δηλαδή προβλήματα γεωμετρίας λύνονται με χρήση γνωστών μεθόδων άλγεβρας.
Ο Ντεκάρτ πέθανε σε ηλικία 54 χρονών στη Στοκχόλμη, ενώ ήταν μέλος της αυλής της βασίλισσας Χριστίνας της Σουηδίας. Εικάζεται οτι ο θάνατός του οφείλεται σε πνευμονία, καθώς η Χριστίνα τον υποχρέωνε να ξυπνάει πολύ νωρίς και να της κάνει διδασκαλία σε πρωινούς περιπάτους· ή, κατ’ άλλους, οφείλεται σε δηλητηρίαση. Ένα σημαντικό μέρος του έργου-του κινδύνεψε να χαθεί κατά τη μεταφορά-του από τη Στοκχόλμη στη Γαλλία, καθώς το πλοίο που το μετέφερε βυθίστηκε στον ποταμό Σηκουάνα, και το μπαούλο που περιείχε τα συγγράμματα του Ντεκάρτ περιμαζεύτηκε επιπλέοντας στα νερά του ποταμού.
Isaac Newton (Ισαάκ Νιούτον, ή Νεύτων, 1643 – 1727)
Τη χρονιά που πέθανε ο Γαλιλαίος, γεννήθηκε μια άλλη μεγάλη μορφή στο χώρο της επιστήμης, και για κάποιους ίσως η μεγαλύτερη όλων των εποχών: ο Άγγλος Isaac Newton (Άιζαακ Νιούτον, ή Ισαάκ Νεύτων — όπως παραδοσιακά επικράτησε να λέγεται στην ελληνική μεταφορά του ονόματός του).
|
|
Ορφανός από πατέρα από τη στιγμή που γεννήθηκε, ο Νιούτον μεγάλωσε με τη γιαγιά-του από την ηλικία των τριών ετών, γιατί η μητέρα-του παντρεύτηκε άλλον άντρα και πήγε να ζήσει μαζί-του. Όταν έγινε 16, η μητέρα-του ήθελε να πείσει το γιο-της να ασχοληθεί με τη γεωργία, αλλά ο διευθυντής του σχολείου-του την έπεισε να τον αφήσει να ολοκληρώσει τη μόρφωσή του. Το 1661 μπήκε στο κολλέγιο, το Trinity College του Cambridge, όπου διδάχθηκε κλασική φιλοσοφία. Το νεαρό Ισαάκ όμως προσήλκυε όχι τόσο ο Αριστοτέλης, όσο οι νεώτεροι φιλόσοφοι και διανοητές, όπως ο Κοπέρνικος, ο Γαλιλαίος, ο Κέπλερ, και ο Ντεκάρτ. Το 1665, όταν εμφανίστηκε μια επιδημία πανούκλας, το πανεπιστήμιό του έκλεισε για λίγο διάστημα, και ο Νιούτον — που είχε στο μεταξύ αποφοιτήσει — αποσύρθηκε στο πατρικό-του σπίτι για τα επόμενα δύο χρόνια. Στη διάρκεια των δύο εκείνων ετών έβαλε τα θεμέλια για αυτά που αργότερα έγιναν γνωστά σαν απειροστικός λογισμός στα μαθηματικά, και νόμος της βαρύτητας στη φυσική. Επίσης τότε ανέπτυξε και τη φυσική θεωρία της οπτικής. Ο Νιούτον, εκτός από τα επιστημονικά-του ενδιαφέροντα, είχε και περίεργες θεολογικές αντιλήψεις, πολύ διαφορετικές από τις ορθόδοξες (με την έννοια της “ορθής δοξασίας”) του κοινωνικού περίγυρού του. Ασχολήθηκε με την αλχημεία, και μετά το θάνατό του βρέθηκε οτι είχε υποστεί δηλητηρίαση από υδράργυρο, χρόνιας μορφής, που μπορεί εν μέρει να εξηγεί τις περίεργες αντιλήψεις-του. |
|
|
 Gottfried Wilhelm von Leibniz (1646 – 1716) |
Στη φυσική, η συμβολή-του είναι εξίσου θεμελιακή. Ουσιαστικά αυτό που ονομάζουμε “κλασική φυσική”, δηλαδή η κινηματική, κλασική μηχανική, και οπτική, φέρει τη σφραγίδα του Νιούτον· γιαυτό και μερικές φορές ονομάζεται “Νευτώνεια φυσική”, ώστε να ξεχωρίζει από τη “σχετικιστική φυσική” του Αϊνστάιν. Μέσω της κλασικής, Νευτώνειας φυσικής, γίνονται σήμερα τα περισσότερα τεχνολογικά επιτεύγματα: από την κατασκευή ενός πολυόροφου κτιρίου μέχρι την πλοήγηση ενός διαστημοπλοίου. Παρόλο που η σχετικιστική φυσική του Αϊνστάιν είναι “πιο σωστή”, στον καθημερινό-μας κόσμο η Νευτώνεια φυσική “φτάνει και περισσεύει” για να δίνει τις λύσεις που χρειαζόμαστε. Η κλασική φυσική του Νιούτον θεωρεί οτι ο τριδιάστατος χώρος είναι “ένα πράγμα”, ενώ ο χρόνος είναι “άλλο πράγμα”, και βασίζεται στην Ευκλείδεια γεωμετρία. Αντίθετα, η σχετικιστική φυσική του Αϊνστάιν θεωρεί οτι χώρος και χρόνος είναι “ένα πράγμα” (ο χωροχρόνος), και βασίζεται σε μη-Ευκλείδεια γεωμετρία. Αυτά όμως θα τα δούμε αργότερα.
Στην κινηματική (κλάδος της φυσικής) είναι γνωστοί οι τρεις νόμοι του Νιούτον. Οι νόμοι αυτοί είναι οι εξής:
| 1ος
νόμος του Νιούτον: Όταν δεν εξασκείται καμία δύναμη σε ένα σώμα, το σώμα είτε είναι ακίνητο, είτε κινείται με σταθερή ταχύτητα. |
Ο πρώτος νόμος εμπεριέχει μια λεπτή φιλοσοφική παραδοχή, που χαρακτηρίζει την κλασική φυσική: το σώμα κινείται ως προς τί; Ο Νιούτον θεώρησε έμμεσα (όπως και όλοι οι φυσικοί μέχρι τον Αϊνστάιν) οτι υπάρχει ο Απόλυτος (και ακίνητος) τριδιάστατος Χώρος, και μέσα σ’ αυτόν κινείται οτιδήποτε κινείται. Επίσης θεώρησε (και πάλι έμμεσα) οτι υπάρχει ο Απόλυτος Χρόνος, που μπορούμε να τον φανταστούμε σαν ένα παγκόσμιο ρολόι, που όταν δίνει έναν χτύπο εδώ στη Γη, δίνει ακαριαία τον ίδιο ακριβώς χτύπο παντού στο σύμπαν, ακόμη και στον πιο απομακρυσμένο γαλαξία. Αυτές οι παραδοχές απορρίφθηκαν αργότερα από τον Αϊνστάιν ως μη συμβατές με τις παρατηρήσεις του 19ου αιώνα.
| 2ος
νόμος του Νιούτον: Ένα σώμα μάζας m στο οποίο εξασκείται μία δύναμη F επιταχύνεται με σταθερή επιτάχυνση a, και η σχέση μεταξύ των τριών ποσοτήτων είναι: F = m · a. |
Στην πραγματικότητα τα F και a είναι διανύσματα, που σημαίνει οτι το σώμα θα επιταχυνθεί (κατά a) κατά την ίδια διεύθυνση κατά την οποία εξασκείται η δύναμη F.
Ο δεύτερος νόμος μας εξηγεί γιατί τα Ι.Χ.-αυτοκίνητα φεύγουν πιο γρήγορα από τα φορτηγά στο πράσινο: παρόλο που η μηχανή του φορτηγού παράγει μεγαλύτερη δύναμη F από αυτήν που παράγει η μηχανή του αυτοκινήτου, εντούτοις το φορτηγό έχει τεράστια μάζα m σε σχέση με το αυτοκίνητο, οπότε η επιτάχυνσή του a είναι πολύ μικρότερη.
| 3ος
νόμος του Νιούτον: Όταν ένα σώμα εξασκεί δύναμη F σε ένα άλλο σώμα, τότε και το δεύτερο σώμα εξασκεί δύναμη –F στο πρώτο σώμα, δηλαδή δύναμη ίσου μεγέθους αλλά αντίθετης φοράς. |
Ο τρίτος νόμος μας λέει για ποιο λόγο δεν μπορούμε να σηκωθούμε στον αέρα τραβώντας τα μαλλιά-μας: παρολο που το τράβηγμα των μαλλιών εξασκεί (μέσω των τριχών) μια δύναμη F στο κρανίο προς τα πάνω, εντούτοις και το κρανίο εξασκεί (πάλι μεσω των τριχών) μια ίση και αντίθετη δύναμη –F στα χέρια προς τα κάτω· οι δύο δυνάμεις αλληλοαναιρούνται, οπότε μένουμε στη θέση-μας.
Ο Νιούτον ήταν ο πρώτος που αντιλήφθηκε οτι η κίνηση του Φεγγαριού γύρω από τη Γη και η πτώση ενός αντικειμένου στη Γη είναι ουσιαστικά το ίδιο φαινόμενο που εμφανίζεται με δύο διαφορετικές όψεις.
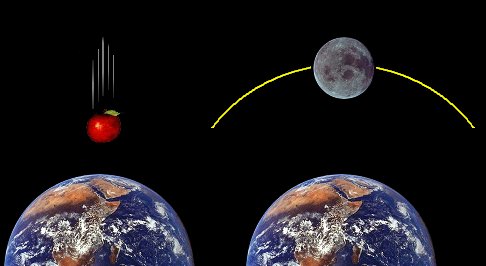
Πτώση μήλου και “πτώση” Σελήνης
Η μόνη διαφορά είναι οτι ένα μήλο, π.χ., που πέφτει προς τη Γη, κατευθύνεται κατακόρυφα κατευθείαν προς το κέντρο της Γης, ενώ η Σελήνη έχει ήδη μια αρχική ταχύτητα παράλληλη με την επιφάνεια της Γης (από τότε που πρωτοδημιουργήθηκε). Ο συνδυασμός αυτής της αρχικής ταχύτητας και της έλξης της Γης κάνει τη Σελήνη να περιφέρεται γύρω από τη Γη (στην πραγματικότητα γύρω από το κοινό κέντρο μάζας του συστήματος Γη–Σελήνη, το οποίο όμως βρίσκεται αρκετά κοντά στο κέντρο της Γης). Αν δώσουμε και στο μήλο μια κατάλληλη αρχική ταχύτητα, τότε και αυτό θα γίνει δορυφόρος της Γης.
Στην οπτική (επίσης κλάδος της φυσικής), ο Νιούτον ασχολήθηκε με τη φύση του φωτός. Κατ’ αρχήν παρατήρησε οτι όταν μια δέσμη ακτίνων λευκού φωτός περνάει μέσα από ένα πρίσμα, παράγεται το φάσμα των χρωμάτων του ουράνιου τόξου (σχήμα).
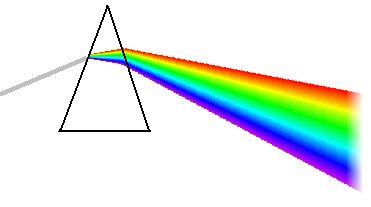
Διάθλαση του φωτός καθώς περνάει μέσα από πρίσμα
Αυτό ο Νιούτον το εξήγησε θεωρώντας οτι το λευκό φως αποτελείται ήδη από όλα αυτά τα χρώματα, και περνώντας μέσα από το πρίσμα το κάθε χρώμα υφίσταται διάθλαση υπό διαφορετική γωνία, οπότε το λευκό φως “αναλύεται” στα συστατικά-του χρώματα. Σήμερα γνωρίζουμε οτι η εξήγηση αυτή είναι κατά βάση σωστή. Το φως δεν αποτελείται από χρώματα, αλλά από φωτόνια, που το καθένα έχει ένα συγκεκριμένο μήκος κύματος, και το μάτι-μας ερμηνεύει το μήκος κύματος σαν χρώμα. Περνώντας μέσα από το πρίσμα, τα φωτόνια υφίστανται τόσο μεγαλύτερη διάθλαση όσο μικρότερο είναι το μήκος κύματός τους. Επειδή το ιώδες χρώμα έχει το μικρότερο μήκος κύματος, αυτά τα φωτόνια διαθλώνται περισσότερο από όλα τα άλλα, ακολουθούμενα από αυτά με μήκος κύματος που ερμηνεύουμε σαν μπλε, κλπ.
Τελικά, σήμερα αναγνωρίζουμε οτι καί ο Νιούτον καί ο Χάιχανς είχαν ο καθένας-τους “από λίγο δίκιο”. Το φως (τόσο το ορατό όσο και το αόρατο, όπως τα μικροκύματα, το υπέρυθρο, το υπεριώδες, οι ακτίνες Χ, οι ακτίνες γάμμα, κλπ) έχει τόσο σωματιδιακή όσο και κυματική φύση. Αποτελείται από φωτόνια, τα οποία όσο διαδίδονται στο χώρο παρουσιάζουν κυματικές ιδιότητες, όταν όμως αλληλεπιδρούν με στοιχειώδη σωμάτια (π.χ. ηλεκτρόνια) τότε συμπεριφέρονται σαν σωματίδια.
Στα 1696 ο Νιούτον διορίστηκε διευθυντής του Βασιλικού Νομισματοκοπείου της Αγγλίας, και το 1705 η βασίλισσα Άννα τον έχρισε “ιππότη”, οπότε πλέον ο Νιούτον έφερε τον τίτλο του Sir. Πρόκειται για τον πρώτο επιστήμονα που ονομάστηκε Sir. Πέθανε το 1727 χωρίς να έχει παντρευτεί ποτέ-του, και χωρίς ν’ αφήσει διαθήκη.
Ο Νιούτον είπε για τον εαυτό-του: «Αν μπόρεσα να δω λίγο μακρύτερα, είναι γιατί στάθηκα πάνω στους ώμους γιγάντων.» Επίσης είπε και το εξής: «Δεν ξέρω με τί μοιάζω για τον υπόλοιπο κόσμο, αλλά στον εαυτό-μου μοιάζω μόνο σαν ένα αγόρι που παίζει στην παραλία, και διασκεδάζει βρίσκοντας τη μια ένα πιο λείο βότσαλο, και την άλλη ένα κοχύλι πιο όμορφο από τα συνηθισμένα, ενώ ο μεγάλος ωκεανός της αλήθειας κείται ολόκληρος και ανεξερεύνητος μπροστά-του.»
Κατασκευή μικροσκοπίου, και η αυγή της βιολογίας
Παρατηρήσεις επί των ιδιοτήτων των έμβιων όντων είχαν γίνει από την αρχαιότητα ακόμα — π.χ. είδαμε οτι ο Αριστοτέλης έγραψε για ζωικά είδη της εποχής-του και του τόπου-του. Όπως όμως και με την αστρονομία, υπάρχουν κάποια όρια μέχρι τα οποία μπορεί να προχωρήσει η παρατήρηση με γυμνό οφθαλμό. Οι πραγματικά κοσμοϊστορικές αστρονομικές ανακαλύψεις έγιναν όταν ο Γαλιλαίος έστρεψε το τηλεσκόπιό του στον ουρανό. Αντίστοιχα, όταν ένας Ολλανδός έμπορος έβαλε κάτω από το μεγεθυντικό φακό-του ύλη που κανείς άλλος δεν είχε σκεφτεί (ή ενδιαφερθεί) να μεγεθύνει πρωτύτερα, ανακάλυψε έναν καινούριο, ανεξιχνίαστο κόσμο: τον κόσμο των μικροοργανισμών (τα πρώτιστα και τα βακτήρια).
 Antonie van Leeuwenhoek (1632 – 1723) |
Ο Ολλανδός έμπορος λεγόταν Antonie van Leeuwenhoek Ο Λέουνχουκ απέκτησε μια σχετική οικονομική άνεση από το εμπόριο κουρτινών που ανέπτυξε στο Ντελφτ (Delft) της Ολλανδίας, και αυτό του επέτρεψε ν’ ασχοληθεί με το χόμπυ-του, που ήταν η κατασκευή φακών μεγάλης μεγέθυνσης και η παρατήρηση του μικρόκοσμου. Μάλιστα δεν ήθελε ν’ αποκαλύψει το μυστικό της τεχνικής με την οποία έφτιαχνε τους φακούς-του, κι άφηνε τον κόσμο να πιστεύει οτι έτριβε το γυαλί μέρα-νύχτα, γιατί έτσι φτιάχνονταν οι φακοί τότε: με διαρκές και υπομονετικό τρίψιμο του γυαλιού με άμμο πολύ λεπτής υφής. |
 Ένα μικροσκόπιό του |
Ο Λέουνχουκ όμως είχε ανακαλύψει μια νέα τεχνική: επαιρνε μια λεπτή βέργα γυαλιού, και τη θέρμαινε στη μέση. Όταν έλιωνε το μέσον-της, το αφαιρούσε, και τραβούσε τα δύο άκρα, κάνοντάς τα να αποκτήσουν στις άκρες-τους δύο πολύ λεπτά “μουστάκια”. Στη συνέχεια πλησίαζε το κάθε “μουστάκι” πάλι στη φλόγα, οπότε εκεί δημιουργιόταν ένα μικρό γυάλινο καθαρό σφαιρίδιο. Αυτό το σφαιρίδιο ήταν ο φακός του μικροσκοπίου-του, με το οποίο πιστεύεται οτι πετύχαινε μεγεθύνσεις ίσως και 500 φορές.
Οι παρατηρήσεις-του άρχισαν να γίνονται γνωστές στη Βασιλική Εταιρεία του Λονδίνου, μέσω της αλληλογραφίας-του. Από κάποιο σημείο και μετά όμως, τα μέλη της Βασιλικής Εταιρείας πέρασαν από τον αρχικό θαυμασμό στην αμφιβολία, γιατί αυτά που τους περιέγραφε ο Λέουνχουκ ήταν πέρα απ’ οτιδήποτε είχαν δει μέχρι τότε οι επιστήμονες της εποχής-του. Για παράδειγμα, ο Λέουνχουκ ισχυριζόταν οτι μέσα σε μια σταγόνα νερό έβλεπε χιλιάδες μικροσκοπικά “ζωύφια” (τα βακτήρια — που τότε αφθονούσαν στο πόσιμο νερό αφού η χλωρίωση του ύδατος ήταν εντελώς άγνωστη). Προβληματισμένη από τις απίστευτες περιγραφές του Λέουνχουκ η Βασιλική Εταιρεία, έστειλε μια επιτροπή στο Ντελφτ, για να ελέγξει την αλήθεια των κειμένων του Ολλανδού. Πράγματι, τα μέλη της επιτροπής είδαν με τα ίδια-τους τα μάτια μερικά από τα “ζωύφια” που παρατηρούσε ο Λέουνχουκ. Όταν επέστρεψαν στο Λονδίνο τον ανακήρυξαν επίτιμο μέλος-τους.
Αυτά που ανακάλυψε ο Λέουνχουκ ήταν ουσιαστικά άλλα είδη ζωής, πέρα από τα φυτά και ζώα (παρόλο που αυτό δεν έγινε κατανοητό στην εποχή-του, παρά μόνο πολύ αργότερα). Η κοινή γνώση των ανθρώπων για την έμβια φύση είναι οτι αυτή αποτελείται από φυτά και ζώα, και τίποτ’ άλλο. Κανένα θρησκευτικό κείμενο (π.χ., Παλαιά ή Καινή Διαθήκη, Κοράνι) δεν αναφέρει οτι ο Θεός έφτιαξε κάτι άλλο εκτός από φυτά και ζώα. Και όμως, τα βακτήρια και τα πρώτιστα που παρατήρησε ο Λέουνχουκ δεν είναι ούτε φυτά ούτε ζώα· είναι δύο άλλα βιολογικά “βασίλεια”, που αποτελούνται από μονοκύτταρους οργανισμούς, συνήθως αόρατους στο γυμνό οφθαλμό. (Υπάρχει και πέμπτο βασίλειο, αυτό των μυκήτων, που περιλαμβάνει ορατούς οργανισμούς όπως οι μούχλες και τα μανιτάρια.) Όμως την εποχή του Λέουνχουκ αυτό δεν ήταν κατανοητό. Έτσι ο Λέουνχουκ δεν ήρθε σε σύγκρουση με την Εκκλησία, αφού υπετίθετο οτι παρατηρούσε απλώς πολύ μικρά φυτά και ζώα.
 |
 |
| Βακτήρια που επιζούν στη
ραδιενέργεια
|
Βακτήρια που ζουν στα έντερα
θηλαστικών
|
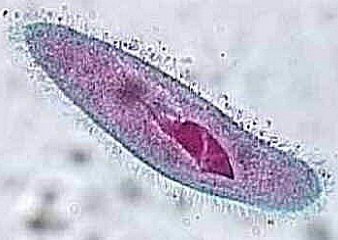 |
 |
| Πρώτιστο (“παραμήκιο”) | Ωκεάνια πρώτιστα (“διάτομα”) |
Οι παραπάνω εικόνες δείχνουν βακτήρια και πρώτιστα (όχι βέβαια σαν εκείνα που παρατήρησε ο Λέουνχουκ)
Ο Λέουνχουκ δεν έγραψε κανένα βιβλίο, μόνο γράμματα τα οποία έστελνε σε γνωστούς και ενδιαφερόμενους, όπου κατέγραφε τις παρατηρήσεις-του, τις οποίες συνέχισε μέχρι το τέλος της ζωής-του. Σήμερα θεωρείται ο πατέρας της μικροβιολογίας.
 Robert Hooke (1635 – 1703) |
Σημαντική μορφή επίσης για την απαρχή της βιολογίας θεωρείται ο Άγγλος επιστήμονας Robert Hooke (Ρόμπερτ Χουκ), του οποίου δυστυχώς δεν σώζεται καμιά προσωπογραφία. (Η εικόνα στ’ αριστερά είναι μια αναπαράσταση του Χουκ που επιχείρησε η ζωγράφος Rita Greer το 2010, βάσει περιγραφών της φυσιογνωμίας-του.) Ο Χουκ ήταν σύγχρονος του Λέουνχουκ, και χρησιμοποίησε μικροσκόπιο του τύπου που χρησιμοποιούμε και σήμερα, δηλαδή αυτό που έχει δύο κύριους φακούς: έναν “αντικειμενικό” (κοντά στο αντικείμενο), και έναν “προσοφθάλμιο” (κοντά στο μάτι). Παρόλο που οι μεγεθύνσεις που πετύχαινε ήσαν κατώτερες εκείνων του Λέουνχουκ, ο Χουκ κατόρθωσε να κάνει σημαντικές παρατηρήσεις. Συγκεκριμένα, ήταν ο πρώτος που διαπίστωσε το γεγονός οτι όλη η έμβια ύλη αποτελείται από κύτταρα, και καθιέρωσε τον όρο αυτόν (αγγλ.: “cell”). |
 Μικροσκόπιο του Χουκ |
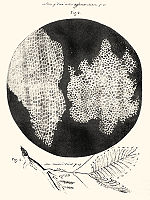
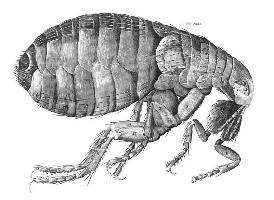
Εικόνες από το έργο του Χουκ, “Μικρογραφία”: κύτταρα φελλού, και ψύλλος
Το γνωστότερο έργο βιολογίας του Χουκ είναι η “Μικρογραφία” (“Micrographia”), όπου βρίσκονται και τα σχέδια που εικονίζονται παραπάνω: η κυτταρική δομή του φελλού, και το σκίτσο ενός ψύλλου. Ο Χουκ όμως έκανε ανακαλύψεις και σε άλλες επιστήμες. Υπάρχει ένας νόμος στη φυσική, ο νόμος της ελαστικότητας, που φέρει το όνομά του. Ο νόμος αυτός επέτρεψε για πρώτη φορά την κατασκευή ωρολογιών με ελατήρια, που μπορούσαν να μετρούν το χρόνο με αποδεκτή ακρίβεια. Περιέγραψε επίσης το νόμο της βαρύτητας, και για το λόγο αυτόν ήρθε σε σύγκρουση με τον Νιούτον, σχετικά με την πατρότητα του νόμου. Παρατήρησε επίσης τους κρατήρες στη Σελήνη, τους δακτύλιους του Κρόνου, και ανακάλυψε τον πρώτο διπλό αστέρα, το γ του Κριού.
Στα χρόνια του Διαφωτισμού
Ο Διαφωτισμός είναι μια περίοδος που — όπως είναι φυσικό — δεν έχει συγκεκριμένη χρονική στιγμή αρχής και τέλους, αλλά οι περισσότεροι ιστορικοί τον τοποθετούν κάπου στον 18ο αιώνα, εκτεινόμενο μέχρι και τον 19ο, φυσικά με ρίζες που φτάνουν όχι μόνο στους αμέσως προηγούμενους αιώνες, αλλά ως την ελληνική αρχαιότητα. Σαν ιδέα, ο Διαφωτισμός χαρακτηρίζεται από την έμφαση στη χρήση του λογικού, δηλαδή του ορθολογισμού, για τη στήριξη απόψεων και τη λήψη αποφάσεων, παρά στην αυθεντία της αρχαίας σοφίας. Κατά τους διανοητές του Διαφωτισμού, η άποψη “όσο πιο αρχαίο τόσο πιο σοφό” είναι λάθος· η σωστή άποψη είναι: “όσο πιο λογικό, τόσο πιο σωστό”. Δεδομένου οτι λογικό είναι επίσης αυτό που είναι συμβατό με την παρατήρηση (αφού είναι παράλογο το να πιστεύουμε κάτι που δεν συμβαδίζει με αυτά που βλέπουμε, ακούμε, πιάνουμε, κλπ.), έπεται η άμεση αλληλοεξάρτηση του Διαφωτισμού με την επιστήμη και με την ανάπτυξη που αυτή παρουσίασε κατά την εποχή εκείνη.
John Dalton (Τζον Ντάλτον, 1766 – 1844), και η θεμελίωση της νεώτερης ατομικής θεωρίας
Όπως είδαμε, η ιδέα οτι η ύλη αποτελείται από διακριτά μικροσκοπικά στοιχεία, αόρατα στο γυμνό οφθαλμό, τα άτομα, είχε ήδη προταθεί από την αρχαιότητα, από τον Δημόκριτο και τον Λεύκιππο. Χρειάστηκε να γίνουν πολλές νέες παρατηρήσεις για να γίνει κατανοητό οτι κάποια υλικά είναι στοιχειώδη (π.χ. το υδρογόνο, το οξυγόνο, ο άνθρακας, κ.ά.), ενώ άλλα υλικά είναι χημικές ενώσεις που αποτελούνται από τα στοιχειώδη υλικά (π.χ. το νερό, η αμμωνία, το μεθάνιο, κ.ά.). Τα θεμέλια της νεώτερης ατομικής θεωρίας (άρα και της χημείας) έβαλε ο Άγγλος επιστήμονας John Dalton (Τζον Ντάλτον).
 |
Ο Ντάλτον δεν υπήρξε μόνο χημικός, αλλά και μετεωρολόγος. Επίσης είναι γνωστός για τη θεωρία περί αχρωματοψίας, δηλαδή την ανικανότητα κάποιων ανθρώπων να βλέπουν ένα ή περισσότερα χρώματα, που λέγεται επίσης “δαλτωνισμός”, προς τιμήν-του. Ο Ντάλτον έπασχε πράγματι από ένα είδος αχρωματοψίας (έβλεπε το κόκκινο σαν γκρίζο, και τα χρώματα πορτοκαλί–κίτρινο–πράσινο του φαίνονταν σαν αποχρώσεις ενός χρώματος, αυτού που ονόμαζε “κίτρινο”), και περιέγραψε την κατάστασή του σε μια εποχή που δεν είχε γίνει ακόμη κατανοητό οτι κάποιοι άνθρωποι δεν βλέπουν όλα τα χρώματα. Πιο γνωστός πάντως έγινε για το οτι διατύπωσε νόμους για τη χημική σύσταση της ύλης. Πρέπει να σημειώσουμε οτι από την αρχαιότητα μέχρι την εποχή του Ντάλτον είχαν ανακαλυφθεί αρκετά νέα στοιχεία, τα περισσότερα μάλιστα τον 18ο αιώνα. Έτσι, είχαν ήδη γίνει γνωστά το άζωτο, ο φωσφόρος, το κοβάλτιο, ο λευκόχρυσος (πλατίνα), το νικέλιο, το υδρογόνο, το φθόριο, το οξυγόνο, το χλώριο, και μερικά άλλα. Ήταν επίσης γνωστό οτι κάποιες άλλες ουσίες (και μερικές πολύ κοινές όπως το νερό), είναι σύνθετες, δηλαδή αποτελούνται από άλλα στοιχεία. |
Κατά τις αρχές του 19ου αιώνα, δηλαδή στα 1800, ο Ντάλτον διατύπωσε τους εξής νόμους. Πρώτα, ένα νόμο που μας έρχεται από την αρχαιότητα:
-
Τα υλικά αποτελούνται από μικροσκοπικά σωματίδια που ονομάζονται άτομα. Τα άτομα δεν μπορούν να δημιουργηθούν, ούτε να χωριστούν σε μικρότερα μέρη. Οι χημικές αντιδράσεις αλλάζουν απλώς τον τρόπο που τα άτομα ενώνονται μεταξύ-τους.
Και στη συνέχεια, τέσσερις επιπλέον νόμους:
-
Κάθε υλικό στοιχείο (π.χ.: υδρογόνο) αποτελείται από ένα και μοναδικό είδος ατόμου.
-
Όλα τα άτομα του ίδιου στοιχείου είναι ταυτόσημα μεταξύ-τους (δεν διαφέρουν σε τίποτα).
-
Άτομα ενός στοιχείου μπορούν να συνδυαστούν με άτομα άλλου στοιχείου και να σχηματίσουν χημικές ενώσεις. Κάθε χημική ένωση αποτελείται πάντα από τον ίδιο αριθμό και είδος ατόμων. (Σήμερα τη στοιχειώδη μονάδα μιας χημικής ένωσης τη λέμε μόριο· δηλαδή ένα μόριο μιας ένωσης αποτελείται από τον ίδιο αριθμό και είδος ατόμων.)
-
Τα άτομα των στοιχείων μπορούν να διαχωριστούν το ένα από το άλλο μέσω των διαφορετικών ατομικών βαρών-τους.
Ο τελευταίος νόμος σημαίνει οτι κάθε άτομο έχει ένα συγκεκριμένο βάρος, που μπορούμε να μετρήσουμε. Ο Ντάλτον έδωσε κατά σύμβαση το βάρος 1 στο άτομο του υδρογόνου, που είναι το ελαφρότερο απ’ όλα τα άτομα. Συνεπώς κάθε άλλο άτομο πρέπει να έχει βάρος μεγαλύτερο από 1.
Δεν είναι όλοι οι νόμοι του Ντάλτον σωστοί από μοντέρνα άποψη. Π.χ. τα άτομα ενός στοιχείου δεν είναι ακριβώς ταυτόσημα μεταξύ-τους, γιατί υπάρχουν τα ισότοπα, δηλαδή άτομα με διαφορετικό αριθμό νετρονίων στον πυρήνα. (Ο αριθμός των πρωτονίων είναι που δίνει την ταυτότητα στο άτομο· τα νετρόνια μπορούν να διαφέρουν.) Εντούτοις για την εποχή εκείνη οι νόμοι του Ντάλτον ήσαν “αρκετά σωστοί” ώστε να βάλουν σε μια στέρεη βάση την περαιτέρω έρευνα στη χημική σύσταση της ύλης.
Carl Friedrich Gauss (Καρλ-Φρίντριχ Γκάους, 1777 – 1855), ο “πρίγκηπας των μαθηματικών”
 Carl Friedrich Gauss |
Οι περισσότεροι μεγάλοι επιστήμονες δεν δείχνουν το οτι θα γίνουν διάσημοι από μικρή ηλικία, και όσοι εμφανίζονται σαν “παιδιά–θαύματα” συνήθως χάνουν σύντομα τη λάμψη-τους μετά την εφηβεία. Ο Γερμανός Καρλ-Φρίντριχ Γκάους όμως αποτελεί εξαίρεση, γιατί υπήρξε τόσο “παιδί–θαύμα”, όσο και ένας από τους μεγαλύτερους μαθηματικούς — ίσως και ο μεγαλύτερος — όλων των εποχών. Είναι δύσκολο να βρεθεί τομέας των μαθηματικών στον οποίον ο Γκάους να μη συνεισέφερε. Σε ηλικία τριών μόλις ετών, λέγεται οτι εξέπληξε τον πατέρα-του όταν υπέδειξε ένα λάθος στις λογιστικές αριθμητικές πράξεις του τελευταίου. Επίσης ο ίδιος ο Γκάους διηγιόταν αργότερα ένα περιστατικό από τη σχολική-του ηλικία: ο δάσκαλος της τάξης είχε βάλει στα παιδιά να αθροίσουν όλους τους αριθμούς από το 1 ως το 100, προφανώς για να βρει λίγη ώρα ησυχίας. Πριν προλάβει όμως να καθίσει καλά-καλά πάλι στην έδρα-του, ο μικρός Καρλ-Φρίντριχ ήρθε με το αποτέλεσμα γραμμένο πάνω στην πλάκα-του: 2050. Πώς το βρήκε; Παρατήρησε οτι αθροίζοντας τους αριθμούς ανά ζεύγη και από τα δύο άκρα δίνει πάντα το ίδιο αποτέλεσμα, δηλαδή: 1+100=101, 2+99=101, 3+98=101, κ.ο.κ. Υπάρχουν 50 τέτοια ζεύγη ως το 50+51=101, επομένως το άθροισμα πρέπει να είναι: 50·101=2050. |
Το περιστατικό αυτό ξεκίνησε μια αλυσσίδα γεγονότων που βοήθησαν τον Γκάους να προχωρήσει στις σπουδές-του. Οι μαθηματικές-του ικανότητες τράβηξαν το ενδιαφέρον του Δούκα του Μπράουνσβάικ (της πόλης όπου ο Γκάους γεννήθηκε και μεγάλωσε), ο οποίος τον έστειλε με υποτροφία στο κολλέγιο, και μετά στο πανεπιστήμιο. Ο Δούκας πέτυχε διάνα στην επιλογή-του, γιατί απο τα χρόνια του πανεπιστημίου ακόμα ο Γκάους άρχισε ν’ αποδεικνύει μια σειρά σημαντικών θεωρημάτων, μεταξύ αυτών και ένα πρόβλημα κατασκευής κανονικών πολυγώνων — προβλήματα που είχαν μείνει άλυτα από την αρχαιότητα. Έμεινε τόσο πολύ ικανοποιημένος από τα αποτελέσματα αυτά, που αφενός αποφάσισε τελειωτικά ν’ ακολουθήσει καριέρα στα μαθηματικά αντί για τη φιλολογία, και αφετέρου — σε προχωρημένη πλέον ηλικία — ζήτησε να χαραχτεί πάνω στον τάφο-του ένα κανονικό δεκαεπτάγωνο (αποτέλεσμα του θεωρήματός του, αφού απέδειξε οτι ένα τέτοιο πολύγωνο μπορεί να κατασκευαστεί με τον “αρχαιοελληνικό περιορισμό”, δηλαδή με τον κανόνα και το διαβήτη). Όμως ο χαράκτης αρνήθηκε, λέγοντας οτι ένα τέτοιο πολύγωνο (με 17 πλευρές!) θα έμοιαζε με κύκλο. Από την αποφοίτησή του το 1799, και μέχρι το θάνατό του το 1855, συνέχισε να παράγει αποτελέσματα όχι μόνο σε όλους τους τομείς των μαθηματικών, αλλά και στην αστρονομία και στη φυσική. Ας δούμε όμως λίγα από τα αμέτρητα ευρήματά του.
Στη στατιστική, η ακόλουθη καμπύλη, η οποία ονομάζεται “Γκαουσιανή” (ή “κανονική”), είναι θεμελιώδους σημασίας:
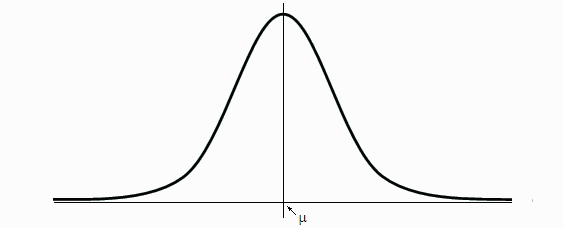
Η καμπύλη αυτή μας δείχνει με ποιον τρόπο κατανέμονται συνήθως οι τυχαίες τιμές μιας μεταβλητής. Παράδειγμα: ας θεωρήσουμε τα ύψη των Ελλήνων ανδρών. Ας μετρήσουμε τα ύψη ενός μεγάλου αριθμού ατόμων, κι ας τα βάλουμε σε κατηγορίες (π.χ.: κατηγορία 1: ύψη μικρότερα του 1,30· κατηγορία 2: ύψη μεταξύ 1,31 και 1,35· κατηγορία 3: ύψη μεταξύ 1,36 και 1,40· κ.ο.κ.). Αν δούμε τώρα πόσα άτομα έπεσαν σε κάθε κατηγορία, και αραδιάσουμε τις κατηγορίες τη μία δίπλα στην άλλη, με μια μπάρα για κάθε κατηγορία που το ύψος-της είναι ανάλογο του αριθμού των ατόμων της κατηγορίας, τότε θα δούμε οτι οι μπάρες σχηματίζουν την Γκαουσιανή καμπύλη, ή “κανονική κατανομή” όπως αλλιώς λέγεται (βλ. σχήμα που ακολουθεί).
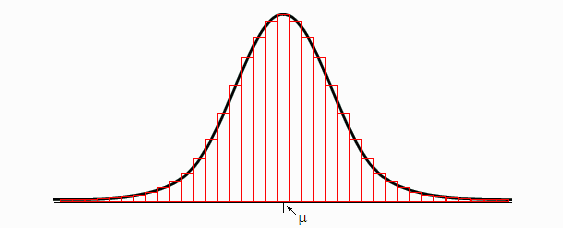
Η κάθε κόκκινη μπάρα, στο παραπάνω διάγραμμα, αντιστοιχεί σε μια κατηγορία ύψους. Η πιο ψηλή μπάρα (δηλαδή η κατηγορία με τα περισσότερα άτομα) βρίσκεται στο μέσο όρο ύψους, που σημειώνεται με το μ. (Π.χ. θα μπορούσε να είναι τα ύψη μεταξύ 1,75 και 1,80 για τους Έλληνες.) Όσο απομακρυνόμαστε από το μέσο όρο, τόσο μικραίνει το πλήθος τον ατόμων ανά κατηγορία. Φυσικά, αυτό δεν ισχύει μόνο για τους άντρες, αλλά και για τις γυναίκες (απλώς ο μέσος όρος των υψών-τους θα είναι μικρότερος). Ούτε μόνο για τα ύψη, αλλά και για τα βάρη. Ούτε μόνο για μετρήσεις ιδιοτήτων ατόμων, αλλά πρακτικά για οποιαδήποτε τυχαία μεταβλητή, όπως για την κατανάλωση νερού ή ηλεκτρικού ανά ημέρα, ή για τον αριθμό των ηλεκτρονικών μηνυμάτων που λαμβάνουμε ανά εβδομάδα. Κάθε τέτοια μεταβλητή ακολουθεί την “κανονική κατανομή”, ή “κατανομή του Γκάους”. Η καμπύλη μπορεί να είναι πιο πλατιά ή πιο στενή, πάντα όμως έχει αυτό το σχήμα, της “κωδωνοειδούς” όπως λέγεται (επειδή μοιάζει με καμπάνα).
Η κανονική κατανομή ήταν μια μόνο από τις συνεισφορές του Γκάους στη στατιστική. (Υπήρξαν κι άλλες, όπως η μέθοδος των ελαχίστων τετραγώνων.) Απέδειξε επίσης θεμελιώδη συμπεράσματα στη θεωρία αριθμών, μιγαδική ανάλυση, γραμμική άλγεβρα, απειροστικό λογισμό, γεωμετρία, διαφορική γεωμετρία, τοπολογία, κ.ά. Πρακτικά, “όποια (μαθηματική) πέτρα κι αν σηκώσει” κανείς, από κάτω θα δει να εμφανίζεται το όνομα του Γκάους. Ασχολήθηκε επίσης με την αστρονομία και τη φυσική. Στην αστρονομία, προέβλεψε και καθόρισε την τροχιά της Δήμητρας, του μεγαλύτερου αστεροειδούς. Ένας κρατήρας στο Φεγγάρι φέρει το όνομά του. Στη φυσική, η μονάδα μαγνητικής επαγωγής (στο σύστημα cgs) ονομάζεται gauss, προς τιμήν-του.
Ο Γκάους, αντίθετα με άλλους μαθηματικούς και επιστήμονες που υπήρξαν πολυγραφότατοι, προτιμούσε να παρουσιάζει λίγα μόνο από τα ευρήματά του στην ευρύτερη μαθηματική κοινότητα, γιατί ήθελε η κάθε δημοσίευσή του να είναι σημαντική και τεχνικά άρτια. Το 1898 (43 χρόνια μετά το θάνατό του) ανακαλύφθηκε το μαθηματικό σημειωματάριό του, το οποίο περιείχε τόσα μαθηματικά αποτελέσματα που έστω και μόνο αυτό το σημειωματάριο να είχε σωθεί, ο Γκάους θα συγκαταλεγόταν μεταξύ των σπουδαίων μαθηματικών. Πολλά συμπεράσματα στα οποία έφτασαν οι μαθηματικοί κατά το δεύτερο μισό του 19ου αιώνα ήσαν ήδη γνωστά στον Γκάους, καθώς περιλαμβάνονταν σ’ εκείνο το σημειωματάριο, παραμένοντας αδημοσίευτα.
Ανάπτυξη μη-Ευκλείδειων γεωμετριών
Όπως είδαμε στην ενότητα περί Ευκλείδειας γεωμετρίας (που είναι αυτή που διδασκόμαστε στο Γυμνάσιο–Λύκειο), ο Ευκλείδης διατύπωσε πέντε αιτήματα, και σημειώσαμε οτι το 5ο αίτημα ακουγόταν αρκετά πιο πολύπλοκο σε σχέση με τα υπόλοιπα τέσσερα. Οι μαθηματικοί λογικά αναρωτιόνταν αν το 5ο αίτημα είναι απαραίτητο, δηλαδή μήπως τυχόν μπορεί ν’ αποδειχτεί σαν συνέπεια των υπόλοιπων 4. (Γιατί αυτό το ερώτημα; Διότι οι μαθηματικοί προσπαθούν πάντα — σύμφωνα με το ξυράφι του Όκαμ — να βρουν την πιο λιτή διατύπωση, και μια θεωρία γεωμετρίας με 4 αιτήματα είναι πιο λιτή από μια με 5, όταν μάλιστα το 5ο αίτημα ακούγεται τόσο πολύπλοκο.) Έγιναν πολλές προσπάθειες ανά τους αιώνες ν’ αποδειχτεί το 5ο αίτημα, όλες όμως άκαρπες. Πολλοί μαθηματικοί νόμισαν οτι κατάφεραν να το αποδείξουν, για να φανεί μετά από λίγο καιρό οτι η απόδειξη ήταν λάθος. Στην πορεία αυτής της έρευνας ανακαλύφθηκαν διάφορες προτάσεις ισοδύναμες με το 5ο αίτημα, δηλαδή προτάσεις που θα μπορούσε να είχε χρησιμοποιήσει κι ο Ευκλείδης αντί για τον τρόπο που διατύπωσε το 5ο αίτημά του. (“Ισοδυναμία” μαθηματικών προτάσεων σημαίνει οτι η μία πρόταση είναι λογική συνέπεια της άλλης, και αντιστρόφως.) Ίσως η απλούστερη πρόταση που είναι ισοδύναμη με το 5ο αίτημα μπορεί να περιγραφεί όπως φαίνεται σχηματικά στο παρακάτω διάγραμμα:
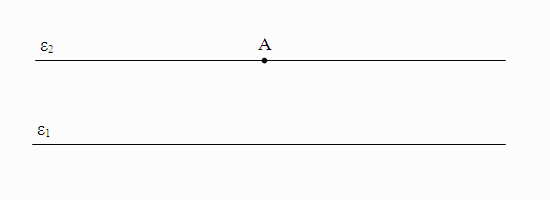
Η πρόταση λέει το εξής: «Από ένα σημείο Α που βρίσκεται εκτός μιας ευθείας ε1 μπορούμε να φέρουμε ακριβώς μία ευθεία ε2 που να περνάει από το Α και να μην τέμνει την ε1 (δηλ. να είναι παράλληλη με την ε1).» Αυτή η διατύπωση, η ισοδύναμη του 5ου αιτήματος, είναι γνωστή σαν “αξίωμα του Playfair”, από τον Σκωτσέζο μαθηματικό John Playfair (Τζον Πλέυφαιρ, 1748 – 1819), που απέδειξε την ισοδυναμία-της με το Ευκλείδειο αίτημα. Επίσης είναι γνωστή και σαν το “αξίωμα της παραλληλίας”.
Ήδη όμως από τις αρχές του 19ου αιώνα, ο Γκάους θεώρησε οτι υπήρχε λόγος που τόσοι και τόσοι μαθηματικοί ανά τους αιώνες είχαν αποτύχει ν’ αποδείξουν το 5ο αίτημα: ο λόγος ήταν οτι δεν υπάρχει απόδειξη, δηλαδή το 5ο αίτημα είναι ανεξάρτητο των άλλων τεσσάρων. Επιπλέον, ο Γκάους άρχισε να εξετάζει τί συμβαίνει όταν το 5ο αίτημα (ή το ισοδύναμό του, “αξίωμα της παραλληλίας”) αντικατασταθεί από κάποιο άλλο, που να λέει π.χ. οτι από ένα σημείο Α εκτός ευθείας ε1 δεν μπορούμε να φέρουμε καμία ευθεία ε2 που να είναι παράλληλη με την ε1· ή οτι μπορούμε να φέρουμε δύο παράλληλες· ή άπειρες στον αριθμό. Καταλήγουμε τότε σε άλλες, μη-Ευκλείδειες γεωμετρίες. Την εργασία-του όμως αυτή δεν τη δημοσίευσε, γιατί φοβόταν την αντίδραση που θα συναντούσε, καθώς επικρατούσε η φιλοσοφική άποψη του Καντ οτι η Ευκλείδεια γεωμετρία ταιριάζει κατά φυσιολογικό τρόπο στο ανθρώπινο πνεύμα, και κατά συνέπεια, αυτή θα πρέπει να είναι η γεωμετρία που καθόρισε ο Θεός για το σύμπαν, ώστε ο κόσμος να είναι συμβατός με —και κατανοητός από — τον ανθρώπινο νου. Ο Γκάους δεν ήθελε ν’ αντιπαρατεθεί με τις θρησκευτικές πεποιθήσεις της εποχής-του.
 János Bolyai |
Το 1831 όμως ο Γκάους έγινε αποδέκτης του βιβλίου ενός νεαρού Μαγυάρου, του János Bolyai (Γιάνος Μπόλιαϊ, 1802 – 1860), μέσω του πατέρα του János και φίλου του Γκάους, Farkas Bolyai. Στο βιβλίο εκείνο ο János Bolyai ανέπτυσσε μια μη Ευκλείδεια γεωμετρία. Ο Γκάους αναγνώρισε τότε τις δικές-του ιδέες, και είπε στον πατέρα Farkas οτι προς την κατεύθυνση αυτή είχε δουλέψει και ο ίδιος τα τελευταία 30 ή 35 χρόνια — πράγμα που εξόργισε τον János, ο οποίος νόμισε οτι ο Γκάους ήθελε να οικειοποιηθεί την εργασία-του. Όπως έγινε όμως γνωστό από την παλαιότερη αλληλογραφία του Γκάους, όντως ο τελευταίος είχε φτάσει σε μη-Εκλείδειες γεωμετρίες από πολλά χρόνια πριν. Εκτός από τον János Bolyai, σε μια μη-Ευκλείδεια γεωμετρία έφτασε το 1829 επίσης ο Ρώσσος Nikolai Ivanovich Lobachevsky. Οι Lobachevsky και Bolyai ανέπτυξαν τις ιδέες-τους προφανώς ανεξάρτητα ο ένας από τον άλλον. |
 N. I. Lobachevsky |
Μπορεί ν’ αναρωτηθεί κανείς τί νόημα έχει να εξετάζονται προτάσεις εναλλακτικές του αξιώματος της παραλληλίας. Δεν είναι προφανές οτι από ένα σημείο εκτός ευθείας μπορούμε να φέρουμε μία και μόνο μία παράλληλη προς την ευθεία; Ποιος ο σκοπός του ν’ αναρωτιόμαστε τί συμβαίνει αν δεν μπορούμε να φέρουμε καμιά παράλληλη, ή αν μπορούμε να φέρουμε δύο ή περισσότερες, όταν αυτά δεν ισχύουν στην πραγματικότητα;
Και όμως, η “πραγματικότητα” που μας φαίνεται οτι “προφανώς ισχύει” (οτι δηλ. μπορούμε να φέρουμε ακριβώς μία παράλληλη), μπορεί να είναι η προσέγγιση μόνο μιας άλλης πραγματικότητας, την οποία αδυνατούμε να συλλάβουμε. Μπορεί να είμαστε σαν τους δέσμιους στην αλληγορία του σπηλαίου του Πλάτωνα. Ας δούμε ένα παράδειγμα: μπορεί αυτό που νομίζουμε οτι είναι επίπεδο να είναι στην πραγματικότητα η επιφάνεια μιας σφαίρας, που είναι όμως εξαιρετικά μεγάλη — τόσο μεγάλη ώστε δεν αντιλαμβανόμαστε την καμπυλότητά της, και νομίζουμε οτι ο χώρος στον οποίο κινούμαστε είναι επίπεδος (βλ. εικόνα που ακολουθεί).
_geometry.jpg)
Ας υποθέσουμε οτι είμαστε “επίπεδα μικρόβια” που ζουν στην επιφάνεια της Γης. Δηλαδή έχουμε εξαιρετικά μικρό μέγεθος σε σχέση με το σύνολο του χώρου στον οποίο θα μπορούσαμε να κινηθούμε (την επιφάνεια της Γης), και είμαστε τόσο επίπεδα όντα που δεν αντιλαμβανόμαστε την τρίτη διάσταση· για μας, ο χώρος έχει μόνο δύο διαστάσεις: μήκος και πλάτος, δηλ. δεν αντιλαμβανόμαστε το ύψος.
Όταν όντα με αυτές τις ιδιότητες μετρούν “μικρά” τρίγωνα, όπως αυτό που φαίνεται στο ένθετο πλαίσιο στα δεξιά, δηλαδή τρίγωνα με μήκη πλευρών τέτοια ώστε τα όντα να είναι τεχνικά σε θέση να τα μετρήσουν, τότε το άθροισμα των γωνιών των τριγώνων βγαίνει οτι είναι πάντα ίσο με 180 μοίρες (180°). Στο σχήμα, στο ένθετο τρίγωνο έχουμε: 40° + 50° + 90° = 180°. Αυτό ακριβώς είναι και το χαρακτηριστικό της Ευκλείδειας γεωμετρίας: οτι κάθε τρίγωνο έχει άθροισμα γωνιών 180°. Μάλιστα η πρόταση αυτή είναι ένα άλλο ισοδύναμο του αξιώματος της παραλληλίας, δηλαδή θα μπορούσαμε να αντικαταστήσουμε το αξίωμα της παραλληλίας (ή το 5ο αίτημα του Ευκλείδη) με την πρόταση: «Το άθροισμα των γωνιών κάθε τριγώνου είναι ίσο με 180°.» Συνεπώς, τα “επίπεδα μικρόβια” νομίζουν οτι ζουν σε ένα χώρο Ευκλείδειας γεωμετρίας δύο διαστάσεων (μήκους και πλάτους).
Το πρόβλημα για τα μικρόβια αυτά είναι οτι δεν μπορούν να ταξιδέψουν πολύ μακριά πάνω στη Γη. Αν μπορούσαν, τότε θα έβλεπαν οτι ένα τρίγωνο όπως αυτό που φαίνεται ζωγραφισμένο πάνω στην επιφάνεια της Γης (αριστερά) μπορεί να έχει άθροισμα γωνιών μεγαλύτερο των 180°. Π.χ. στο σχήμα: 50° + 90° + 90° = 230°. Τα μικρόβια θα καταλάβαιναν τότε οτι κάθε τρίγωνο έχει άθροισμα γωνιών μεγαλύτερο των 180° — ακόμα και τα μικρά τρίγωνα του άμεσου περιβάλλοντός τους, μόνο που για τέτοια τρίγωνα το άθροισμα των γωνιών είναι τόσο λίγο πάνω από τις 180° που τα όργανα μέτρησης των μικροβίων δεν έχουν την απαιτούμενη τεράστια ακρίβεια για να μετρήσουν ένα άθροισμα όπως π.χ. το 180.00000005°, και να δουν οτι αυτό διαφέρει από το “ακριβώς 180°”. Επίσης, αν τα μικρόβια μπορούσαν να ταξιδέψουν μακριά πάνω στη Γη, θα διαπίστωναν οτι όλες οι γραμμές που τους φαίνονται ευθείες έχουν μια κύρτωση, και άρα όλες οι ευθείες που τους φαίνονται παράλληλες τέμνονται· όμως στο άμεσο περιβάλλον-τους η κύρτωση αυτή είναι αμελητέα και δεν μπορούν να την αντιληφθούν, νομίζοντας οτι οι παράλληλες ευθείες δεν τέμνονται πουθενά, προεκτεινόμενες έως το άπειρο.
Έτσι τα μικρόβια αυτά σιγά-σιγά (μετά από πολλαπλές και όλο πιο ακριβείς παρατηρήσεις) θα καταλάβαιναν οτι ο χώρος-τους είναι κυρτωμένος μέσα σε μια τρίτη διάσταση, κι οτι η γεωμετρία που ισχύει στην πραγματικότητα είναι η σφαιρική γεωμετρία (όπως ονομάζεται αυτή η μη-Ευκλείδεια γεωμετρία)· και οτι ο χώρος του άμεσου περιβάλλοντός τους τους φαίνεται να είναι “προφανώς Ευκλείδειος” (όπως θα νόμιζε ο δικός-τους Καντ), κι οτι αυτό συμβαίνει επειδή η σφαιρική γεωμετρία πλησιάζει την Ευκλείδεια όταν η περιοχή του χώρου στην οποία γίνονται οι μετρήσεις είναι πολύ μικρή σε σχέση με την όλη σφαίρα.
Τώρα, ποια από τα στοιχεία αυτής της “αλληγορίας των μικροβίων” μεταφέρονται και ισχύουν στη δική-μας περίπτωση;
Ισχύει το οτι ο χώρος του άμεσου περιβάλλοντός μας είναι πολύ μικρός, οπότε αν το σύμπαν έχει μια καμπυλότητα, δεν μπορούμε να την αντιληφθούμε, και νομίζουμε οτι ο χώρος-μας είναι “επίπεδος σε 3 διαστάσεις”, δηλαδή οι ευθείες μας φαίνονται ευθείες και όχι καμπύλες. Ισχύει επομένως το οτι νομίζουμε πως ζούμε σε Ευκλείδειο χώρο, ενώ ο χώρος μπορεί και να είναι μη-Ευκλείδειος. Στην περίπτωση αυτή όμως δεν ισχύει το οτι η γεωμετρία του χώρου-μας είναι υποχρεωτικά σφαιρική. Πρόσφατες παρατηρήσεις δείχνουν ένα χώρο επίπεδο, με προσέγγιση 99%. Μπορεί να είναι όντως επίπεδος (Ευκλείδειος) με καμπυλότητα μηδέν, ή να έχει μια εξαιρετικά μικρή καμπυλότητα που δεν μπορούμε ακόμα να παρατηρήσουμε. Π.χ. μπορεί να είναι σφαιρικός, με σφαιρική γεωμετρία που έχει όπως λέμε θετική καμπυλότητα· ή να έχει αρνητική καμπυλότητα, οπότε η γεωμετρία που του ταιριάζει είναι η υπερβολική γεωμετρία. Σε γεωμετρίες με αρνητική καμπυλότητα, όπως η υπερβολική, τα τρίγωνα έχουν άθροισμα γωνιών μικρότερο των 180°, και από ένα σημείο εκτός ευθείας μπορούμε να φέρουμε άπειρες παράλληλες προς την ευθεία. Αντίθετα, στη σφαιρική γεωμετρία (που πιο γενικά λέγεται ελλειπτική) δεν μπορούμε να φέρουμε καμία παράλληλη γιατί όλες οι ευθείες τέμνονται. Μπορούμε να συνοψίσουμε όλα αυτά στον παρακάτω πίνακα:
|
Καμπυλότητα | Αξίωμα παραλληλίας | Άθροισμα γωνιών τριγώνου | ||
| Σφαιρική (ή ελλειπτική) | θετική ( > 0 ) | καμία παράλληλη | > 180° | ||
| Ευκλείδεια | μηδέν ( = 0 ) | μία παράλληλη | = 180° | ||
| Υπερβολική | αρνητική ( < 0 ) | άπειρες παράλληλες | < 180° |
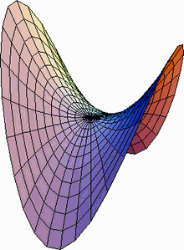
Υπάρχει καμιά επιφάνεια στην οποία να μπορούμε να “δούμε” την υπερβολική γεωμετρία, όπως υπάρχει η σφαίρα για τη σφαιρική γεωμετρία; Βεβαίως. Υπάρχει το “υπερβολικό παραβολοειδές”, γνωστό και ως “σαμάρι”, λόγω του σχήματός του που μοιάζει με σέλλα (διάγραμμα, αριστερά).
 |
 |
| Υπερβολικό παραβολοειδές, μια
επιφάνεια με μεταβλητή αρνητική καμπυλότητα |
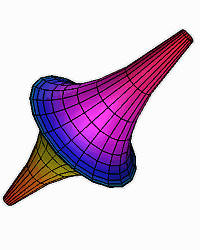
Ψευδοσφαίρα, μια επιφάνεια με
σταθερή αρνητική καμπυλότητα, π.χ. ίση με –1 |
Το σχήμα στα δεξιά έχει κι αυτό αρνητική καμπυλότητα, και μάλιστα με σταθερή τιμή. Λέγεται “ψευδοσφαίρα”, γιατί η κανονική σφαίρα έχει επίσης σταθερή αλλά θετική καμπυλότητα, π.χ. ίση με 1, ενώ η ψευδοσφαίρα μπορεί να έχει καμπυλότητα ίση με –1. Δεν είναι δύσκολο να δούμε οτι τα τρίγωνα πάνω στις επιφάνειες αυτές έχουν άθροισμα γωνιών μικρότερο των 180°. Βέβαια στις παραπάνω επιφάνειες η γεωμετρία είναι δύο διαστάσεων. Όταν μιλάμε για το χωροχρόνο του σύμπαντός μας, μιλάμε για γεωμετρία τεσσάρων διαστάσεων.

Bernhard Riemann
Μεταξύ των μαθηματικών που ασχολήθηκαν με μη-Ευκλείδειες γεωμετρίες, εξέχουσα θέση κατέχει ο Γερμανός Bernhard Riemann (Μπέρναρντ Ρίμαν, 1826 – 1866), μαθητής του Γκάους, που δυστυχώς πέθανε πολύ νέος. Πρόλαβε όμως, στη σύντομη σταδιοδρομία-του, να γενικεύσει τη γεωμετρία ώστε η νέα θεωρία να περιλαμβάνει σαν ειδικές περιπτώσεις όλες τις γεωμετρίες που συζητήθηκαν μόλις παραπάνω (ελλειπτική, Ευκλείδεια, υπερβολική), και μάλιστα σε ένα χώρο ν-διαστάσεων. Η θεωρία αυτή λέγεται Ριμάνεια γεωμετρία, και αποτελεί τη μαθηματική βάση της θεωρίας της γενικής σχετικότητας.
Τα παραπάνω όμως, περί μη-Ευκλείδειων γεωμετριών, θεωρούνταν απλώς μια “μαθηματική παραξενιά” κατά το 19ο αιώνα, γιατί κανένας δεν φανταζόταν οτι η γεωμετρία του σύμπαντός μας μπορεί να μην είναι Ευκλείδεια. Μόνο με την έλευση του 20ού αιώνα και τη διατύπωση της θεωρίας της γενικής σχετικότητας από τον Αϊνστάιν (το 1915–16) έγινε κατανοητό οτι η “μαθηματική παραξενιά” ήταν η ίδια η πραγματικότητα. Γι’ αυτά όμως θα μάθουμε αργότερα. Ο 19ος αιώνας γνώρισε κι άλλα κοσμοϊστορικά επιτεύγματα.
Ηλεκτρομαγνητική θεωρία: Michael Faraday και James Clerk Maxwell
Από την αρχαιότητα είχαν παρατηρηθεί τα φαινόμενα του ηλεκτρισμού και του μαγνητισμού. Μάλιστα οι δύο λέξεις έχουν αρχαία ελληνική προέλευση (ο “ηλεκτρισμός” από το ήλεκτρο, ή κεχριμπάρι, επειδή όταν το τρίβουμε π.χ. πάνω σε μάλλινη επιφάνεια δημιουργείται “στατικός ηλεκτρισμός” — όπως τον ονομάζουμε σήμερα — μέσω του οποίου το ήλεκτρο έλκει μικρά και ελαφρά αντικείμενα, π.χ. τρίχες, ή κομματάκια χαρτί· και ο “μαγνητισμός” από την “μαγνήτιν λίθον”, ένα σιδηρούχο ορυκτό που εξορυσσόταν στην περιοχή της Μαγνησίας της Μικράς Ασίας, και παρουσιάζει έντονα φαινόμενα μαγνητισμού). Τα δύο φαινόμενα όμως, του ηλεκτρισμού και του μαγνητισμού, δεν είχαν συνδεθεί μεταξύ-τους και θεωρούνταν διαφορετικά.
 Michael Faraday (1791 – 1867) |
Η σύνδεση μεταξύ των δύο φαινομένων έγινε κατά το 19ο αιώνα, κυρίως από δύο Βρετανούς: τον Άγγλο Michael Faraday (Μάικλ Φάραντέυ, 1791 – 1867), και τον Σκωτσέζο James Clerk Maxwell (Τζέιμς Κλερκ Μάξουελ, 1831 – 1879). Ο Faraday σαν επιστήμονας ήταν αυτοδίδακτος. Γιος σιδηρουργού, έπρεπε να ξεπεράσει πολύ μεγάλα κοινωνικά εμπόδια στη Βικτωριανή εποχή της Βρετανίας προκειμένου να ανελιχθεί και να γίνει αποδεκτός από τους άλλους επιστήμονες. Διέθετε όμως εξαιρετικό πάθος και ικανότητα στην πειραματική έρευνα. Έτσι, παρατήρησε το φαινόμενο της ηλεκτρικής επαγωγής, όταν, τυλίγοντας δύο μονωμένα καλώδια γύρω από ένα σιδερένιο δακτύλιο, και διοχετεύοντας ρεύμα στο ένα καλώδιο, παρατήρησε ένα στιγμιαίο ηλεκτρικό ρεύμα στο άλλο καλώδιο. Σύντομα παρατήρησε και οτι ηλεκτρικό πεδίο μπορούσε να δημιουργηθεί επίσης όταν κινούσε ένα μαγνήτη κοντά σε τυλιγμένο καλώδιο. |
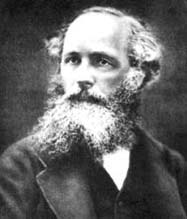 James Clerk Maxwell (1831 – 1879) |
Η γενικευμένη αρχή της ηλεκτρομαγνητικής επαγωγής λέει οτι ένα ηλεκτρικό πεδίο που αλλάζει τιμή προκαλεί τη δημιουργία ενός μαγνητικού πεδίου (όσο αλλάζει)· αλλά επίσης και οτι ένας κινούμενος μαγνήτης προκαλεί τη δημιουργία ενός ηλεκτρικού πεδίου. Αυτή είναι η αρχή πάνω στην οποία στηρίζονται οι ηλεκτρομαγνήτες, που χρησιμοποιούνται σήμερα ευρέως, από απλές ηλεκτρικές συσκευές που περιλαμβάνουν πηνία (ψυγεία, πλυντήρια, κουζίνες, κλπ), μέχρι τους γιγάντιους γερανούς που ανυψώνουν φορτία σε οικοδομικές εργασίες.
Άλλη σπουδαιότατη εφεύρεση του Faraday (μεταξύ πολλών) ήταν το ηλεκτρικό δυναμό, δηλαδή η μετρατροπή της κινητικής ενέργειας σε ηλεκτρική ενέργεια. Το δυναμό το βλέπουμε σε άμεση εφαρμογή στο φαναράκι του ποδηλάτου που ανάβει από την περιστροφική κίνηση της ρόδας, αλλά και σε πιο ουσιαστική εφαρμογή στα υδροηλεκτρικά εργοστάσια και στις ανεμογεννήτριες (βλ. “αιολική ενέργεια”), που μετατρέπουν την κίνηση του νερού ή του ανέμου σε ηλεκτρισμό.
Τις ανακαλύψεις του Faraday και των άλλων επιστημόνων πάνω σε ηλεκτρικά και μαγνητικά φαινόμενα κατάφερε να συνθέσει σε μία θεωρία ο Maxwell, κατά μία γενεά νεώτερος του Faraday. Ο Maxwell κατάφερε να συνοψίσει σε ένα σύνολο μερικών εξισώσεων την ιδέα οτι ο ηλεκτρισμός, ο μαγνητισμός, και ακόμα και το φως, αποτελούν τρεις όψεις ενός και του αυτού φαινομένου: της ύπαρξης ηλεκτρομαγνητικού πεδίου. Έτσι, τα ηλεκτρομαγνητικά πεδία κινούνται στο χώρο με τη μορφή κυμάτων, και με την ταχύτητα του φωτός. Το φως δεν είναι παρά ηλεκτρομαγνητική ακτινοβολία, και σαν τέτοια έχει κυματική φύση (πράγμα που, κατά το 19ο αιώνα, δικαίωσε προσωρινά τον Χάιχανς και αδίκησε τον Νιούτον).
Την εποχή του Maxwell υπήρχε ακόμα το ερώτημα του μέσα σε ποιο μέσο διαδίδεται το φως. Κάθε άλλο γνωστό τότε κύμα ήταν κατανοητό οτι διαδίδεται σε ένα μέσον· π.χ., για τα ηχητικά κύματα, το μέσον είναι ο αέρας· για τα θαλάσσια κύματα, το μέσον είναι το νερό. Για τα κύματα του φωτός όμως ποιο θα μπορούσε να είναι το μέσον; Είναι δυνατόν ποτέ τα φωτεινά κύματα να διαδίδονται στο κενό, χωρίς μέσον; Αυτό το ερώτημα οδήγησε πολλούς επιστήμονες τότε να υποθέσουν οτι το φως διαδίδεται σε ένα ειδικό μέσον, που το ονόμασαν αιθέρα, δανειζόμενοι τη λέξη από τη θεωρία των τεσσάρων στοιχείων (ή καλύτερα πέντε, καθώς ο αιθέρας ήταν το πέμπτο) των Εμπεδοκλή–Αριστοτέλη. Σύμφωνα με την άποψη αυτή, ο αιθέρας διαποτίζει και διαπερνά τα πάντα στο σύμπαν, και αποτελεί ένα σταθερό “σημείο αναφοράς” μέσω του οποίου ορίζεται ο χώρος του σύμπαντος. Αυτή η ιδέα, που είναι λανθασμένη, έπαιξε θεμελιώδη ρόλο στην αντικατάσταση της κλασικής (Νευτώνειας) φυσικής από τη σχετικιστική φυσική (του Αϊνστάιν) στις αρχές του 20ού αιώνα, όπως θα δούμε αργότερα. Είναι επίσης ένα καλό παράδειγμα λαθεμένης ιδέας που προτάθηκε όχι για να εξηγηθούν κάποια πειραματικά δεδομένα (αφού κανένα πείραμα δεν είχε γίνει που να παρατηρούσε απευθείας τον αιθέρα), αλλά για να ικανοποιηθεί μια φιλοσοφική άποψη (“κάθε κύμα πρέπει να έχει ένα μέσο μέσα στο οποίο διαδίδεται”).
Charles Darwin (Τσαρλς Ντάργουϊν, ή Κάρολος Δαρβίνος, 1809 – 1882), και η θεωρία της εξέλιξης των ειδών
Μετά από τις θεμελιώδεις ανακαλύψεις που είχαν γίνει στη φυσική και στη χημεία μέχρι τα μέσα του 19ου αιώνα, ήρθε και η σειρά της βιολογίας να κάνει κ’ εκείνη το δικό-της άλμα προς την κατανόηση του φυσικού κόσμου. Συναντήσαμε τα πρώτα βήματα στη βιολογία με την ανακάλυψη των βακτηρίων και πρωτίστων από τον Λέουνχουκ, και την ανακάλυψη των κυττάρων από τον Χουκ. Επίσης, το 1866 ο Αυστριακός (Γερμανός στην καταγωγή) ιερέας Gregor Mendel (Γκρέγκορ Μέντελ, 1822 – 1884), δημοσίευσε την εργασία-του για ορισμένα κληρονομικά χαρακτηριστικά σε φυτά από μπιζέλια, που έγινε η βάση της γενετικής επιστήμης, αλλά πολλά χρόνια αργότερα, μετά το θάνατό του. Καμία όμως από αυτές τις ανακαλύψεις δεν είναι δυνατό να συγκριθεί με τη “θεωρία της εξέλιξης των ειδών μέσω φυσικής επιλογής”, του Τσαρλς Ντάργουϊν (ή Κάρολου Δαρβίνου), ως προς το μέγεθος της επίδρασης που είχε στη συνολική επιστημονική θεώρηση και κατανόηση του φυσικού κόσμου.
 O Charles Darwin, σε ηλικία 72 ετών, ένα χρόνο πριν το θάνατό του. |
Ο Ντάργουϊν γεννήθηκε στην Αγγλία, και από μικρός έδειξε έφεση στη φυσική ιστορία και στις συλλογές διαφόρων ειδών. Σε ηλικία 8 ετών έχασε τη μητέρα-του, οπότε και εισήχθη στο σχολείο της πόλης-του (το Shrewsbury) σαν οικότροφος. Από το 1825 βοηθούσε τον πατέρα-του που ήταν γιατρός, και σπούδαζε ιατρική, αλλά έβρισκε τις διαλέξεις βαρετές και τις εγχειρήσεις ψυχολογικά πιεστικές, οπότε παράτησε τις ιατρικές σπουδές-του. Αυτό ενόχλησε τον πατέρα-του, που τον έστειλε στο Christ’s College του Cambridge, προκειμένου να σπουδάσει θεολογία, ώστε να γίνει Αγγλικανός ιερέας. Αντί να διαβάζει όμως, ο νεαρός Ντάργουϊν προτιμούσε να συλλέγει σκαθάρια με τους φίλους-του — δημοσίευσε κιόλας μερικές από τις ανακαλύψεις-του. Πάντως όταν ήρθε ο καιρός των εξετάσεων, ο Ντάργουϊν στρώθηκε στο διάβασμα, και μάλιστα του άρεσε πολύ η γλώσσα και το ύφος του William Paley, στο Αποδείξεις του Χριστιανισμού. Το τέλος των σπουδών-του τον βρήκε αποδεχόμενο μια πρόσκληση για ταξίδι με το πλοίο HMS Beagle — που επρόκειτο να χαρτογραφήσει τις Νοτιοαμερικανικές ακτές — σαν σύντροφος του καπετάνιου Robert FitzRoy. Ο Ντάργουϊν αποδέχτηκε την πρόσκληση σε ένα ταξίδι που θα έπαιζε κρίσιμο και αποφασιστικό ρόλο στη διαμόρφωση της σκέψης-του, και όπως αποδείχτηκε, και στην πορεία της ανθρωπότητας γενικότερα. Το ταξίδι με το Beagle διήρκεσε σχεδόν πέντε χρόνια, στη διάρκεια των οποίων ο Ντάργουϊν έκανε ένα μεγάλο αριθμό γεωλογικών και βιολογικών παρατηρήσεων, πλουτίζοντας τις συλλογές-του. |
Μεταξύ των παρατηρήσεών του περιλαμβάνονται εκείνες όπου παρατήρησε κοχύλια ενσωματωμένα σε πετρώματα βρισκόμενα σε μεγάλο υψόμετρο, στην οροσειρά των Άνδεων. Αυτό τον έκανε να συμπεράνει οτι εντός τεράστιων γεωλογικών περιόδων (πολλών εκατομμυρίων ετών) το έδαφος που κάποτε αποτελούσε τον πυθμένα ωκεανών υψώνεται και έρχεται στην επιφάνεια, σχηματίζοντας νέα νησιά και ηπείρους· και αντίστροφα: γη που αποτελούσε νησιά και ηπείρους βυθίζεται και αποτελεί πλέον τον πυθμένα ωκεανών. (Τη θεωρία αυτή δεν την πρότεινε πρώτος ο Ντάργουϊν, αλλά την είδε να επιβεβαιώνεται, και έπαιξε σπουδαίο ρόλο στη θεωρία της εξέλιξης των ειδών.) Έκανε επίσης σημαντικές παρατηρήσεις στα νησιά Γκαλάπαγος του Ειρηνικού (δυτικά του σημερινού Εκουαδόρ) που αποτελούν σχετικά νέο γεωλογικό σχηματισμό, και όπου η πανίδα έχει εξελιχθεί με ιδιάζοντα τρόπο (πράγμα που συμβαίνει σε όλα τα απομονωμένα νησιωτικά περιβάλλοντα).
Παρόλο που οι παρατηρήσεις-του από το ταξίδι με το Beagle τον έκαναν διάσημο στην Αγγλία, ο Ντάργουϊν δεν δημοσίευσε τη θεωρία-του περί της εξέλιξης των ειδών για σχεδόν 20 χρόνια. Στο μεταξύ συνέχισε να επεξεργάζεται τη θεωρία-του με νέα δεδομένα από παρατηρήσεις, ενώ παράλληλα δούλευε σε διάφορα άλλα επιστημονικά θέματα. Όμως τον Ιούνιο του 1858 έλαβε γράμματα από τον 35-χρονο Ουαλλό φυσιοδίφη, εξερευνητή, και βιολόγο, Alfred Russel Wallace (Άλφρεντ Ράσσελ Ουάλλας, 1823–1913) — με τον οποίο ο Ντάργουϊν βρισκόταν ήδη σε επικοινωνία — όπου ο Ουάλλας σκιαγραφούσε τη θεωρία της εξέλιξης, την οποία ο Ντάργουϊν θεωρούσε αποκλειστικά προϊόν της δικής-του έρευνας και σκέψης! Έτσι ο Ντάργουϊν αισθάνθηκε την ανάγκη να επισπεύσει την έκδοση ενός βιβλίου που είχε ήδη σχεδόν τελειώσει, οπότε το Νοέμβριο του 1859 εμφανίστηκε στα ράφια των βιβλιοπωλείων του Λονδίνου το «Περί της προέλευσης των ειδών, μέσω φυσικής επιλογής», τα πρώτα αντίτυπα του οποίου πουλήθηκαν σχεδόν αμέσως. Το βιβλίο αυτό έμελλε ν’ αλλάξει τον τρόπο με τον οποίο αντιλαμβανόμαστε το φυσικό κόσμο των έμβιων όντων σήμερα.
Πώς ορίζεται η θεωρία της εξέλιξης μέσω φυσικής επιλογής;
Σαν θεωρία, μπορεί να διατυπωθεί όπως π.χ. η θεωρία της Ευκλείδειας γεωμετρίας, βασιζόμενη σε ορισμένα αξιώματα (θεμελιώδεις παραδοχές). Τα αξιώματα αυτά εύκολα μπορεί να δει κανείς οτι ισχύουν στο φυσικό κόσμο, και είναι τα εξής:
|
♦ Υπάρχει ένας πληθυσμός από οντότητες, που έχουν την ιδιότητα να αναπαράγονται, δηλαδή να δημιουργούν αντίγραφα του εαυτού-τους. ♦ Οι οντότητες–αντίγραφα (“τέκνα”) δεν είναι απόλυτα πιστές, αλλά έχουν μικροατέλειες (“μεταλλάξεις”)· πάντως είναι αρκετά πιστές ώστε να χαρακτηρίζονται σαν αντίγραφα των αρχικών οντοτήτων (“γονέων”). ♦ Οι οντότητες υπάρχουν μέσα σε ένα περιβάλλον από το οποίο προσλαμβάνουν συστατικά (“τροφή”) και στο οποίο αποβάλλουν άλλα συστατικά (“περιττώματα”)· έχουν δηλαδή μεταβολισμό. ♦ Το περιβάλλον είναι πεπερασμένο, δηλαδή δεν μπορεί να συντηρήσει άπειρο αριθμό οντοτήτων μέσω των συστατικών-του. ♦ Καμία οντότητα δεν εξακολουθεί να υπάρχει (“ζει”) επ’ άπειρο· δηλαδή κάποτε καταστρέφεται (“πεθαίνει”) και αποδίδει στο περιβάλλον τα συστατικά από τα οποία αποτελείται. |
Βασιζόμενοι στις παραπάνω απλές παραδοχές, μπορούμε να κατασκευάσουμε ένα σύστημα, ακόμα και μέσω προσομοίωσης στον υπολογιστή, στο οποίο να παρατηρήσουμε την εξέλιξη των οντοτήτων να συμβαίνει σε πραγματικό χρόνο, “μπροστά στα μάτια-μας”. Δεν είναι δηλαδή η θεωρία της εξέλιξης μια αφηρημένη φιλοσοφική θεωρία που μπορεί να ισχύει, ή μπορεί και όχι — ανάλογα με τις προτιμήσεις του εκάστοτε φιλοσόφου — αλλά ένα λογικό–μαθηματικό οικοδόμημα (όπως η γεωμετρία), που μπορεί να επαληθευτεί μέσω υπολογιστικών συστημάτων που το υλοποιούν. Παράδειγμα ενός τέτοιου υπολογιστικού συστήματος δίνεται στο μάθημα Β3 (“Εξέλιξη ειδών”).
Τί είναι η θεωρία της εξέλιξης με απλά λόγια;
Η θεωρία γίνεται εύκολα κατανοητή με ένα απλό παράδειγμα: πώς οι καμηλοπαρδάλεις απέκτησαν τους πανύψηλους λαιμούς-τους.
Αρκετά εκατομμύρια χρόνια πριν, οι καμηλοπαρδάλεις δεν είχαν ψηλούς λαιμούς, αλλά έμοιαζαν με τους σημερινούς μακρινούς συγγενείς-τους, τα οκάπι — ένα σπάνιο ζώο που ζει και σήμερα σε δάση της κεντρικής Αφρικής (φωτογραφία).

Οκάπι, μακρυνός (αλλά και ο σημερινός κοντινότερος!) συγγενής της καμηλοπάρδαλης
Μάλιστα και οι καμηλοπαρδάλεις (ή μάλλον οι μακρινοί πρόγονοι των σημερινών ζώων) ζούσαν σε δασώδεις εκτάσεις. Σε διάρκεια εκατοντάδων χιλιάδων ετών όμως, το περιβάλλον-τους στην Αφρική άλλαξε. Τα δάση όπου ζούσαν οι καμηλοπαρδάλεις άρχισαν να αποψιλώνονται, και να μετατρέπονται σε Αφρικανική σαβάννα, δηλαδή ανοιχτή έκταση με χαμηλή βλάστηση, όπου αραιά και πού εμφανίζεται κάποιο μοναχικό δέντρο. Η αλλαγή όμως από δάσος σε σαβάννα δεν έγινε απότομα, αλλά σταδιακά. Έτσι, οι πρόγονοι των καμηλοπαρδάλεων (που αρχικά είχαν κοντούς λαιμούς όπως τα σημερινά οκάπι) προσαρμόστηκαν σιγά-σιγά στην αλλαγή, ώστε να φτάνουν σε όλο και ψηλότερα φυλλώματα δένδρων: των δέντρων που “αντιστέκονταν” στην αλλαγή και δεν εξαφανίζονταν (οι απόγονοι των οποίων είναι τα σημερινά ψηλά αλλά σπάνια δέντρα της σαβάννας). Η πιο σημαντική ιδέα είναι οτι η προσαρμογή αυτή δεν γίνεται στη διάρκεια της ζωής ενός και μοναδικού ζώου· δηλαδή δεν “μακραίνει ο λαιμός” του ζώου επειδή τον τεντώνει για να φτάσει τα ψηλότερα φύλλα. Η προσαρμογή συμβαίνει στη διάρκεια πολλών γενεών. Δηλαδή: από όλα τα μικρά που θα γεννήσει το ζώο-πρόγονος, κάποια θα έχουν ελαφρώς ψηλότερο λαιμό, και κάποια ελαφρώς κοντύτερο από το γονέα, απλά και μόνο επειδή ποτέ τα “αντίγραφα” (τα τέκνα) δεν είναι πανομοιότυπα με τα “πρωτότυπα” (τους γονείς), όπως απαιτεί η δεύτερη θεμελιώδης παραδοχή της θεωρίας της εξέλιξης (βλέπε πλαίσιο, παραπάνω). Η διαφορά στο μήκος του λαιμού μεταξύ γονέα και τέκνου μπορεί να είναι μόνο μερικά χιλιοστά του μέτρου. Αυτά τα λίγα χιλιοστά ομως, δίνουν στο τέκνο ένα σημαντικό ποσό επιπλέον τροφής, λόγω του συνολικού αριθμού των δέντρων. Η επιπλέον τροφή για το ελαφρώς ψηλότερο ζώο συνεπάγεται ελαφρώς καλύτερη υγεία, και άρα ελαφρώς περισσότερους απογόνους από τον αδερφό ή αδερφή-του που έτυχε να έχει κάπως κοντύτερο λαιμό. Οι απόγονοί του θα κληρονομήσουν — κατά μέσο όρο πάντα — τον ψηλότερο λαιμό. Όσο το περιβάλλον συνεχίζει να αλλάζει, με δέντρα που γίνονται όλο και ψηλότερα, τόσο οι λαιμοί των ζώων θα “αντικατοπτρίζουν” κατά κάποιον τρόπο την ιδιότητα αυτή του περιβάλλοντος. Και γενικά, αυτή είναι μια πολύ σημαντική έννοια στην εξελικτική θεωρία: οτι τα έμβια όντα αντικατοπτρίζουν το περιβάλλον, όπου ο όρος “περιβάλλον” περιλαμβάνει και άλλα έμβια όντα.
Σήμερα έχουμε επιπλέον γνώση για το πώς συμβαίνουν τα παραπάνω, χάρη στα όσα γνωρίζουμε περί DNA, γονιδίων, κλπ. Την εποχή του Ντάργουϊν όμως η γνώση αυτή δεν υπήρχε. Αντίθετα, οι Ντάργουϊν, Ουάλλας, κλπ, έπρεπε να “παλαίψουν” εναντίον ιδεών όπως εκείνες του Λαμάρκ (ορίστε το πλήρες όνομά του — κρατηθείτε: — Jean-Baptiste Pierre Antoine de Monet Chevalier de la Marck, 1774 – 1829), σύμφωνα με τις οποίες ο λαιμός του ζώου όντως — υποτίθεται — μακραίνει επειδή το ζώο τον τεντώνει για να φτάσει την τροφή-του, και μάλιστα το χαρακτηριστικό αυτό περνάει και στους απογόνους-του. (Ο Λαμάρκ υποστήριζε οτι ο γιος του σιδερά είναι μυώδης επειδή ο πατέρας-του έκανε μεγάλους μυς δουλεύοντας το σίδερο στο αμόνι.) Σήμερα γνωρίζουμε οτι τα κληρονομικά χαρακτηριστικά μεταβιβάζονται μόνο μέσω γονιδίων, τα οποία βρίσκονται στα ωάρια και σπερματοζωάρια των ατόμων, και φυσικά δεν εξαρτώνται από το τί κάνει το άτομο στη διάρκεια του βίου-του.
Ο Ντάργουϊν έγραψε και άλλα βιβλία που παραμένουν κλασικά, όπως τα “Η προέλευση του ανθρώπου”, και “Η έκφραση των συναισθημάτων στον άνθρωπο και στα ζώα”. Ακόμα κι αν δεν είχε γράψει το “Περί της προέλευσης των ειδών”, θα ήταν γνωστός σαν ένας σημαντικός βιολόγος, που απάντησε στο ερώτημα του πώς σχηματίζονται οι κοραλλιογενείς ύφαλοι και νήσοι (οι ατόλλες), και που περιέγραψε με μεγάλη λεπτομέρεια και σαφήνεια την χλωρίδα και πανίδα της Νότιας Αμερικής. Εντούτοις το βιβλίο “Περί της προέλευσης των ειδών” επισκιάζει όλο το υπόλοιπο έργο-του.
Η θεωρία της εξέλιξης είναι σημαντική όχι μόνο στη βιολογία, αλλά και όπου υπάρχουν “οντότητες” που δημιουργούν όχι-απόλυτα-ακριβή αντίγραφα του εαυτού-τους. Τέτοιες “οντότητες” είναι π.χ. οι γλώσσες, γιαυτό και έχουμε εξέλιξη των γλωσσών, που παρουσιάζει χαρακτηριστικά πολύ παρόμοια με εκείνα της εξέλιξης των βιολογικών ειδών, όπως μαθαίνουμε στο μάθημα Γ4 (“Εξέλιξη Γλωσσών”). Επίσης “οντότητες” είναι και οι ιδέες (νοήματα, ή “μιμίδια”) στους νους των ανθρώπων· και εκεί υπάρχει ένα είδος εξέλιξης, με τα δικά-του ειδικά χαρακτηριστικά (βλ. μάθημα Ν2: “Νους – Έννοιες”). Βλέπουμε λοιπόν οτι η έννοια της εξέλιξης ξεπερνά τα στενά όρια της βιολογίας· εξ ου και η σπουδαιότητά της στη συνολική εικόνα που έχουμε αποκτήσει για το φυσικό κόσμο.
Dmitri Ivanovich Mendeleev (Ντμίτρι Ιβάνοβιτς Μεντελέεβ, 1834 – 1907), και ο περιοδικός πίνακας των στοιχείων
Σε προηγούμενα εδάφια είδαμε οτι από τον 17ο αιώνα και μετά άρχισαν ν’ ανακαλύπτονται ραγδαία τα χημικά στοιχεία, το ένα μετά το άλλο. Το κάθε χημικό στοιχείο έχει έναν ατομικό αριθμό, που είναι ο αριθμός των πρωτονίων στον πυρήνα-του. Ο ατομικός αριθμός είναι κάτι σαν τον αριθμό ταυτότητας. Π.χ., το στοιχείο άνθρακας (χημικό σύμβολο: C) έχει 6 πρωτόνια στον πυρήνα-του, άρα ατομικό αριθμό 6. Αν προστεθεί άλλο ένα πρωτόνιο, τότε δεν έχουμε πλέον τον άνθρακα, αλλά το στοιχείο άζωτο (σύμβολο: Ν), με ατομικό αριθμό 7. Με ένα επιπλέον πρωτόνιο, έχουμε το επόμενο στοιχείο, το οξυγόνο (Ο) με ατομικό αριθμό 8· κ.ο.κ.
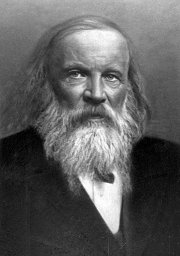 |
Όμως τα περί πρωτονίων δεν ήσαν ακόμη γνωστά κατά το 19ο αιώνα. Οι χημικοί τότε δεν ήξεραν περί ατομικού αριθμού, αλλά περί ατομικού βάρους, που είναι ο μέσος όρος της μάζας των ατόμων ενός στοιχείου, διαιρεμένος δια το 1/12 της μάζας ενός ατόμου του άνθρακα 12C (δηλαδή του ατόμου με 6 πρωτόνια και 6 νετρόνια). Το ατομικό βάρος εξαρτάται όχι μόνο από το πόσα πρωτόνια, αλλά και από το πόσα νετρόνια έχει ο πυρήνας του στοιχείου, αφού και αυτά συνεισφέρουν στο πόσο βαρύ είναι το κάθε άτομο. Οι χημικοί του 19ου αιώνα προσπαθούσαν να βρουν κάποια σχέση μεταξύ ατομικού βάρους και ιδιοτήτων του κάθε στοιχείου. Ένας απ’ αυτούς, ο Ρώσσος Dmitri Ivanovich Mendeleev (Ντμίτρι Ιβάνοβιτς Μεντελέεβ, 1834 – 1907), παρατήρησε οτι όταν διαρρύθμιζε τα στοιχεία σε σειρές και στήλες, τότε έβλεπε κάποιες νομοτέλειες μεταξύ ατομικών βαρών και ιδιοτήτων των στοιχείων. Σημαντικό είναι επίσης οτι ο Μεντελέεβ παρατήρησε πως για να ισχύουν οι νομοτέλειες θα έπρεπε να υποθέσει οτι κάποια στοιχεία έλειπαν από ορισμένες σειρές και στήλες, δηλαδή δεν είχαν ανακαλυφθεί ακόμη. Έτσι ο Μεντελέεβ μπόρεσε και προέβλεψε την ύπαρξη στοιχείων άγνωστων μέχρι τότε, με συγκεκριμένες ιδιότητες και ατομικά βάρη. Τα στοιχεία που έλειπαν ανακαλύφθηκαν τα επόμενα χρόνια, ή δεκαετίες. |
Ο Μεντελέεβ δημοσίευσε τον πρώτο περιοδικό πίνακα των στοιχείων το 1869. Την εποχή που κατασκεύασε τον πίνακα ήσαν γνωστά 63 στοιχεία (από τα 92 συνολικά “φυσικά” χημικά στοιχεία, δηλαδή αυτά με ατομικό αριθμό μικρότερο ή ίσο του ουράνιου). Το στοιχείο ήλιο (με ατομικό αριθμό 2) είχε ανακαλυφθεί το 1868, και θα ήταν το 64ο, αλλά αυτό δεν ήταν ακόμη γνωστό στον Μεντελέεβ. Αν τοποθετήσουμε τα 63 γνωστά τότε στοιχεία στον πίνακα, έτσι όπως θα μπορούσε να τον παρουσιάσει ο Μεντελέεβ, παίρνουμε τον εξής περιοδικό πίνακα (τα άγνωστα μέχρι τότε στοιχεία σημειώνονται με γκρίζα γράμματα στο σχεδιάγραμμα):
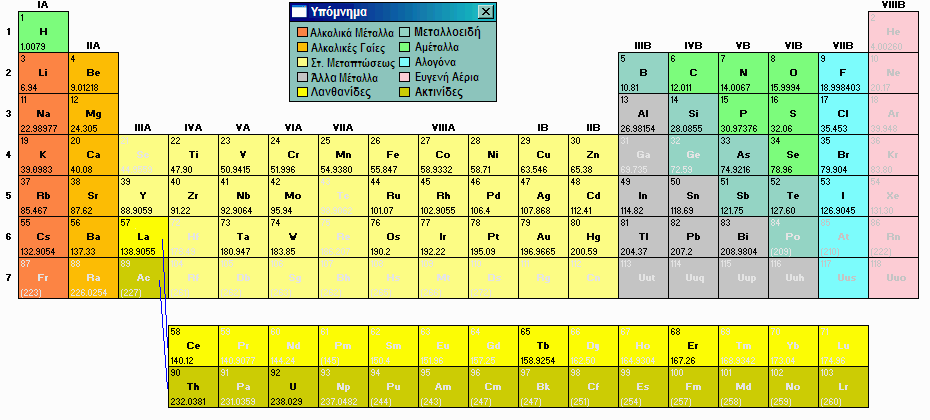
Στον παραπάνω πίνακα (όπως και στον πλήρη, που ακολουθεί), σημειώνεται το σύμβολο του στοιχείου στο κέντρο κάθε τετραγώνου (π.χ. Au = χρυσός), ο ατομικός αριθμός πάνω-αριστερά (π.χ. 79 για τον χρυσό), που ήταν άγνωστος στον Μεντελέεβ, και το ατομικό βάρος-του κάτω-αριστερά (π.χ. 196,9665 για τον χρυσό). Βλέπουμε οτι την εποχή του Μεντελέεβ ήσαν εντελώς άγνωστα τα ευγενή αέρια (δεξιά στήλη, ροζ χρώμα). Επίσης ήσαν τόσο λίγα στοιχεία γνωστά από τις λανθανίδες και ακτινίδες, που ο Μεντελέεβ δεν μπορούσε να κατατάξει τα στοιχεία εκείνα σε οποιεσδήποτε ομάδες, οπότε παρουσιάζονταν σαν “ξεκάρφωτα”.
Ο περιοδικός πίνακας με όλα τα στοιχεία που έχουν ανιχνευτεί μέχρι σήμερα (2010), έχει ως εξής:
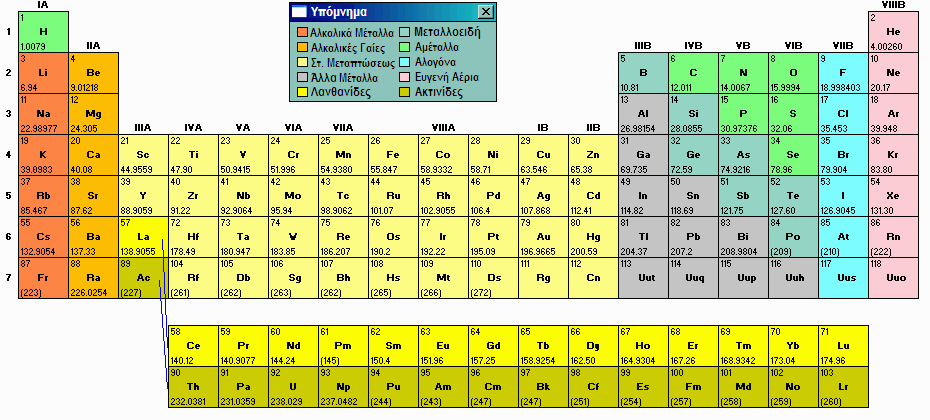
Ο πίνακας λέγεται “περιοδικός” γιατί κάθε σειρά-του είναι μια “περίοδος”, δηλαδή οι ιδιότητες των στοιχείων επαναλαμβάνονται περιοδικά. Τα στοιχεία που έχουν παρόμοιες ιδιότητες σημειώνονται με το ίδιο χρώμα· π.χ.: πορτοκαλί = αλκαλικές γαίες· κυανό = αλογόνα· ροζ = ευγενή αέρια· κλπ.
Ένα στοιχείο που πρωτοανιχνεύθηκε το 1955, αυτό με ατομικό αριθμό 101, ονομάστηκε “Μεντελέβιο” (σύμβολο: Md), προς τιμήν του Μεντελέεβ.
Ανακάλυψη ακτίνων Χ, και επέκταση της έννοιας “φως” σε “ηλεκτρομαγνητικό φάσμα”
 Wilhelm Röntgen |
Προς τα τέλη του 19ου αιώνα υπήρχε μεγάλο ενδιαφέρον για το φως, τον ηλεκτρισμό, και τις ιδιότητές τους. Πολλοί ερευνητές πειραματίζονταν με συσκευές που χρησιμοποιούσαν είτε φως, είτε ηλεκτρισμό, ή και τα δύο. Ένας απ’ αυτούς ήταν ο Γερμανός Wilhelm Röntgen (Βίλεμ Ρέντγκεν, 1845 – 1923), που κατά το 1895 πειραματιζόταν με καθοδικές λυχνίες στις οποίες διοχέτευε ηλεκτρισμό. Ένα βράδυ, στις 8 Νοεμβρίου 1895, προκάλεσε ηλεκτρική εκκένωση σε μια καθοδική λυχνία στην οποία είχε ανοίξει ένα παραθυράκι στο πλάι, που το είχε σκεπάσει με φύλλο αλουμινίου, και από πάνω με μαύρο χαρτόνι. Είχε χαμηλώσει πολύ το φωτισμό στο δωμάτιο για να ελέγξει μήπως ξέφευγε καθόλου φως από το παραθυράκι της λυχνίας. Όντως, δεν έβγαινε καθόλου φως από εκεί, αλλά με έκπληξη παρατήρησε οτι ένα φιλμ από πλατινοκυανίδιο του βαρίου, που έτυχε να βρίσκεται εκεί κοντά, φωσφόριζε μέσα στο σκοτάδι. |
 Το χέρι της κυρίας Röntgen |
Τις επόμενες μέρες πειραματίστηκε εξετάζοντας διεξοδικά τις μυστηριώδεις ακτίνες που ξέφευγαν από τη λυχνία, τις οποίες ονόμασε “ακτίνες Χ” (δανειζόμενος την έννοια “άγνωστος x” από τα μαθηματικά). Διαπίστωσε οτι οι ακτίνες διαπερνούσαν πολλά αδιαφανή αντικείμενα, συμπεριλαμβανομένου και του ανθρώπινου σώματος. Χρησιμοποιώντας το χέρι της συζύγου-του, Anna Bertha Röntgen, αποτύπωσε σε φωτογραφική πλάκα την πρώτη ακτινογραφία στην ιστορία της ανθρωπότητας (βλ. εικόνα, παραπάνω, όπου το σκούρο αντικείμενο στο δάχτυλο είναι ένα δαχτυλίδι). Όταν η Anna Bertha κοίταξε την πλάκα, αναφώνησε: «Είδα πλέον το θάνατό μου!»
Η σπουδαιότητα των ακτίνων Χ (ή “ακτίνων Röntgen”, όπως τις ονόμασαν άλλοι επιστήμονες) για την εξέταση των οστών του ανθρώπινου σώματος έγινε αμέσως αντιληπτή, και το 1901 ο Röntgen έλαβε το πρώτο βραβείο Νόμπελ φυσικής, καθώς ο θεσμός των Νόμπελ ξεκίνησε μόλις τότε. Το 2004, το χημικό στοιχείο υπ’ αριθ. 111 ονομάστηκε Ρεντγκένιο (Roentgenium), προς τιμήν-του.
Αρχικά οι ακτίνες Χ θεωρούνταν ένα “νέο είδος ακτίνων”. Αργότερα όμως, ο Max von Laue και οι μαθητές-του έδειξαν οτι οι ακτίνες Χ δεν είναι παρά φως με συχνότητα σημαντικά μεγαλύτερη από τις συχνότητες που αντιλαμβανόμαστε σαν ορατό φως. Δηλαδή: το φως, χάρη στην κυματική-του φύση, υπάρχει σε διάφορες συχνότητες· αλλά το ανθρώπινο μάτι είναι σε θέση να αντιληφθεί ένα εξαιρετικά περιορισμένο εύρος συχνοτήτων: αυτών που βλέπουμε στο ουράνιο τόξο, και που ονομάζουμε “ορατό φάσμα”, δηλαδή από το κόκκινο έως το ιώδες. Το φάσμα του φωτός όμως, που λέγεται “ηλεκτρομαγνητικό φάσμα”, περιλαμβάνει πολύ περισσότερες συχνότητες που δεν τις βλέπουμε· τόσο μικρότερες του κόκκινου χρώματος, όσο και μεγαλύτερες του ιώδους, όπως δείχνει το παρακάτω διάγραμμα. Οι ακτίνες Χ ανήκουν στο τμήμα του φάσματος με συχνότητες πολύ μεγαλύτερες του ιώδους χρώματος.
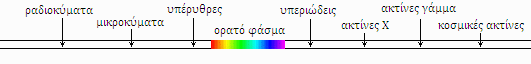
Το ηλεκτρομαγνητικό φάσμα
Βέβαια την εποχή του Röntgen δεν ήσαν γνωστά άλλα τμήματα του ηλεκτρομαγνητικού φάσματος. Όσο πιο προς τα δεξιά κοιτάμε στο παραπάνω διάγραμμα, τόσο πιο μεγάλες είναι οι συχνότητες και οι ενέργειες των φωτεινών (αλλά αόρατων) κυμάτων, και τόσο πιο μεγάλη διαπερατότητα έχουν τα κύματα, δηλαδή τόσο πιο εύκολα εισχωρούν και διαπερνούν την ύλη. Οι ακτίνες γάμμα, π.χ., έχουν ακόμη μεγαλύτερη διαπερατότητα από τις ακτίνες Χ. Επίσης, όσο πιο μεγάλη η ενέργεια των ακτίνων, τόσο πιο καταστρεπτικές είναι για τους ζωντανούς ιστούς. Οι υπεριώδεις ακτίνες, π.χ., μας προκαλούν το γνωστό μαύρισμα μετά από έκθεση στον ήλιο, αλλά η πολύ παρατεταμένη έκθεση σ’ αυτές μπορεί να προκαλέσει καρκινώματα στο δέρμα· οι ακτίνες Χ είναι πιο επικίνδυνες, γιαυτό οι γιατροί δεν επιχειρούν περισσότερες ακτινογραφίες απ’ όσες είναι απολύτως απαραίτητες για μια διάγνωση· τέλος, οι ακτίνες γάμμα, που δημιουργούνται π.χ. κατά την έκρηξη πυρηνικής βόμβας, είναι θανατηφόρες ακόμα και σε μικρές δόσεις. (Οι κοσμικές ακτίνες δεν είναι φως, αλλά σωματίδια με ενέργειες ακόμα μεγαλύτερες εκείνων των ακτίνων γάμμα, που φτάνουν στη γη από το διάστημα.)
Πίσω στη γενική σελίδα του Διαδικτυακού Επιστημονικού Πανεπιστημίου


