 |
Scientific Method and PrinciplesLECTURE NOTES FOR COURSE S1 OF I.C.S.
|
|
Purpose and Nature of This Course
This course examines the foundations of science. It helps the student understand what science is and what it is not. Upon completing it, the student should be able to tell whether a given domain of knowledge can be justifiably called “scientific” or not. It should be noted that, although this course examines fundamental scientific notions, itself is not scientific but philosophical in nature. It couldn’t be otherwise, after all. The foundations of a domain of knowledge cannot be defined from within the domain itself, because such an endeavor would lead to a circular edifice, therefore a logically unsupported one; the foundations lie necessarily outside of the domain. Hence, the foundations of science are not scientific, but philosophical.
What Today’s Science Is Concerned with
In Latin, the word “scientia” originally meant “knowledge” (of any kind). The corresponding Greek word was “episteme” (ἐπιστήμη). Today, from “scientia” we have the word “science” in English, whereas from “episteme” we get the adjective “epistemic”. Over the course of the millennia, however, and especially in the last few centuries, the meaning of “scientia” (or rather its incarnations in various languages with roots in Latin, such as “science” in English) shifted to something more specific than “domain of knowledge”; it came to mean that particular knowledge which is acquired by the use of the scientific method — the latter will be discussed thoroughly, being the focus of this course — and which examines the natural world. The philosophical domain that examines the principles of how knowledge (including the scientific knowledge) is acquired, is called “epistemology”. This course is one in scientific epistemology.
Now, what exactly constitutes the “natural world” is not so trivial. Clearly physicists, chemists, biologists, astronomers, and geologists (among others) are concerned with the natural world, whereas lawyers, theologians, and philosophers (among others) are not. But what about linguists? Their object of study, which is the principles of language, is an abstract product of human beings, who are physical; so linguists are scientists as long as they employ the (yet to be explained) scientific method. So are psychologists and cognitive scientists, since their object of study is cognition, another abstract product of a physical object: the brain. What about mathematicians? Although their primary object of study, i.e., numbers, is an abstract product of human cognition, mathematicians do not employ straightforwardly the scientific method (at least not nowadays; a case could be made for ancient mathematicians); so mathematics is not part of “science proper”, but rather an indispensable tool for science. Superficially a similar justification can be made for astrology: although it discusses the natural world, astrologers do not employ the scientific method; so astrology is not science. However, astrology and mathematics could not be more different: mathematics, as we said, is a tool for science, whereas astrology violates scientific principles in many ways, such as when it assumes relations between the objects it is concerned with (e.g., between planets and people’s birth events) — relations that are scientifically unsupported. But let’s proceed to learn what the most indispensable ingredient of science is: the scientific method.
The Scientific Method
There is a cycle that is followed so that the acquired human knowledge becomes part of scientific knowledge. This cycle consists of the following stages:
-
observation
-
initial theory – predictions
-
experiment – data collection
-
modified theory & predictions
-
publication
-
criticism
Note that not all of the above stages of the cycle are mandatory. Also, the cycle usually starts looping from the stage of the experiment and on. Now let’s examine the stages in detail.
Observation
The original observation (or observations) refers to some property of the physical world, which is observed either by one person, or by a team of people, and either accidentally, or as part of a conscious effort to perform observations.
Here is an example of an accidental observation made by one person:
In February, 1896, the French scientist Henri Becquerel was examining pieces of uranium, which he would leave for a day exposed to the sun; later, when he put them on a photographic film (of that time) he could get the imprint of the metal on the film. Becquerel explained this by assuming that the energy of the sunlight gathered into the metal during the day, so that later, when that energy leaked out of the metal, it was imprinted on the photographic film. One day, he took a fresh piece of uranium, but because the day was cloudy, lacking sunlight, he put it in his drawer, on top of a photographic film. After a couple of days, when he took the piece of uranium out of the drawer, to his great surprise, he saw that the metal had left its imprint on the film, although that piece had never been exposed to the sunlight. Becquerel concluded that uranium had inherently the ability to imprint itself on the film. He had discovered, by accident, the phenomenon of radioactivity.
And here is an example of observation which is the result of a conscious effort for discovery:
By the turn of the 19th century, astronomers had realized that there were irregularities in the data of orbits of the planets Uranus and Neptune. So they suspected that there could be an additional planet, beyond Neptune, which was responsible for those irregularities. The American astronomer Percival Lowell started and funded the research. However, no result was obtained until his death, in 1916. Only on February 18, 1930, the — also American — young astronomer Clyde Tombaugh observed a faint little star that had changed its position on two successive photographs that had been taken within two weeks. The “little star” was planet Pluto. (At that time, and until 2006, Pluto was considered to be the 9th planet; but in 2006 it was officially “demoted” to the category of dwarf planets.)
This kind of conscious effort for observation can sometimes result in the almost comical situation of “correct by error!” In reality, such is the case of the discovery of Pluto, because the size and orbit of Pluto didn’t explain the irregularities observed in the orbits of Uranus and Neptune. Eventually, it was shown that the irregularities were due to errors of the observations of the 19th century! If those errors had not been committed, the search for the ninth planet would not have been initiated. More famous, however, is the case of the first “confirmation” of the theory of general relativity, which skyrocketed Einstein’s international prestige. Whereas general relativity is — as far as we know today — correct (and Einstein is justifiably worth of his fame), however, the first confirmation of his theory was made in the wrong way. Specifically, in 1919, Sir Arthur Eddington took pictures of the solar eclipse that happened during that year, and computed how much the light of a star near the Sun was curved. Eddington found a curvature value that agreed with the prediction of the theory of relativity. Later it was proposed that Eddington’s calculations included errors, without which he would have found a curvature value insufficient to confirm the theory (or to reject it). However, the errors were made, and the theory was “confirmed” in 1919. Of course, later many accurate confirmations of the theory of relativity were performed (and continue being performed).
So we see that in order to make observations after a conscious effort there must already exist a theory that makes predictions, which are issues that will be examined immediately. Observations made by accident that lead to scientific discoveries are more impressive, and there is an English word for that concept: serendipity. But let’s see what a theory is.
Theory
The observations create a set of data, and the scientist’s purpose is to come up with a theory that explains the observed data and that predicts new ones. For example, suppose we see the following numbers:
7, 14, 21, 28, 35, 42, ...
The question is: which number follows and must be expected in the place of the three dots?
Usually it takes no more than a few seconds to see that the above sequence is the multiples of seven; therefore, since 42 = 6 x 7, it follows that the next number must be 49 = 7 x 7.
The above example is a simplified abstraction of the process of creating a theory out of prior observations. The observations, or “data”, are the numbers 7, 14, 21, 28, 35, and 42. The “theory” that we create out of those numbers is: “Multiples of 7.” Having a theory that explains the data we can answer the question: “Which is the next number?” That is, we can make a prediction. And this is one feature that separates science from all the rest of knowledge: through science we can predict the future, at least with some degree of certainty (which, however, is never 100%, as we’ll soon see).
Let’s examine another, visual–geometric example. Suppose the data consists of the following numbers: 2, 9, 14, 17, 18, 17, 14, 9, 2.
Those numbers could be the temperatures recorded by a thermometer during the daytime at regular intervals — e.g., every one hour. However, it’s not important what they represent or how they were collected; what’s important is that we have a quite high degree of certainty for their accuracy, so that we regard them as data. (A later section explains how degrees of certainty are estimated.) Now we are after a theory that explains our data. We notice that if we arrange the numbers 2, 9, 14, 17, 18, 17, 14, 9, and 2 at regular intervals according to their magnitudes, we obtain the following diagram:
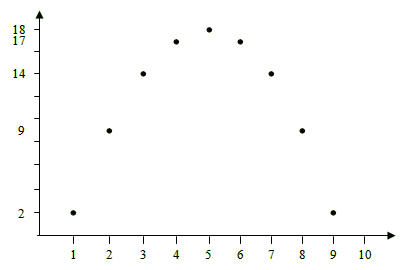
Every dot corresponds to one datum (number), and has
been placed
at a height proportional to its size: the 1st datum at a height of 2,
the 2nd at a height of 9, the 3rd at 14, and so on.
We see that the data are not random but form a pattern. Specifically, it is as if they trace a curve. That curve is the theory that explains the data. Let’s connect the dots with the curve that they seem to trace:
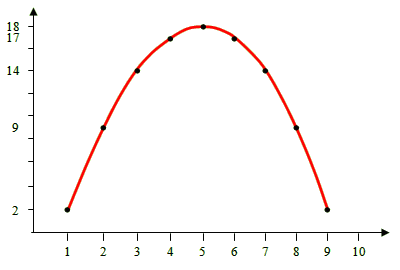
We can even give a mathematical form to the red curve, or theory: it is the “function” y = 18 – (x – 5)2. For each value of x (that is, for x = 1, x = 2, x = 3, etc), we obtain one of our data as the value of y (y = 2, y = 9, y = 14, etc).
Armed now with the theory “y = 18
– (x – 5)2![]() ”,
we can attempt some predictions: we can predict that the 10th
number must be –7 (minus seven). This follows if we substitute the value
10 for x in our function (or theory), so we obtain the value –7 for y.
So, if the above data were indeed degrees of temperature (say, in centigrade), our
theory predicts that at the end of the next one hour the temperature
will drop to –7
degrees (seven below zero). Such predictions can prove useful in real
life. (E.g.: “If the temperature is going to drop to –7, I better wear
my heavy winter-coat”, etc.)
”,
we can attempt some predictions: we can predict that the 10th
number must be –7 (minus seven). This follows if we substitute the value
10 for x in our function (or theory), so we obtain the value –7 for y.
So, if the above data were indeed degrees of temperature (say, in centigrade), our
theory predicts that at the end of the next one hour the temperature
will drop to –7
degrees (seven below zero). Such predictions can prove useful in real
life. (E.g.: “If the temperature is going to drop to –7, I better wear
my heavy winter-coat”, etc.)
Also, the discovery of the theory “y =
18 – (x – 5)2![]() ”
gives us the feeling of satisfaction that now we “understood” somewhat
better what those numbers are, since we have a concise description
of them through the theory “y =
18 – (x – 5)2
”
gives us the feeling of satisfaction that now we “understood” somewhat
better what those numbers are, since we have a concise description
of them through the theory “y =
18 – (x – 5)2![]() ”.
We say that the theory is a “concise description”
because it can generate (predict) for us not only the given numbers but
many more, as many as we want: prior, in-between, and future ones, which
we never measured with our thermometer.
”.
We say that the theory is a “concise description”
because it can generate (predict) for us not only the given numbers but
many more, as many as we want: prior, in-between, and future ones, which
we never measured with our thermometer.
Moving now to a real rather than artificial example, with a theory obtained from observations from reality and yielding true predictions, consider the solar eclipses. Having at our disposal a multitude of observations of the positions of the Sun and Moon (and of the other planets) on the imaginary dome of the sky, we can construct a theory that describes how the heavenly bodies move in time. Thus, we can predict their positions at any future moment, knowing when the disk of the Moon will cover partly (or even fully) the disk of the Sun, causing a solar eclipse. So, we know for example that one of the next total solar eclipses visible from the northern hemisphere will take place on August 2, 2027.

Total solar eclipse
Let it be noted that even ancient peoples could predict eclipses, although they had a wrong theory about the solar system. That is, they considered the Earth as immovable and lying at the center of the universe, while all other heavenly bodies moved around it. This theory, which is called geocentric, is more complex than the heliocentric one (which has the Sun — in Greek: Helios — at the center), and makes calculations harder. Now, if the only thing we are interested in is the motion of heavenly bodies as we see them from Earth, then the geocentric theory (or: “Ptolemaic model”) is not “wrong”, but merely more complicated. But if we are interested in journeys through space, then we will realize in a very painful way that the geocentric theory is wrong when our spaceship is warped by the gravity field of the moving Earth and is lost in space. In the case of journeys through space there are additional data (e.g., the observer’s location in 3D-space) that are ignored by the theory that we call “geocentric”. Therefore, whether a theory is “good” or not depends on how many of the data it explains, and on what purpose we need it for.
In later sections of this course we’ll examine theories, and also their relations with data, in more detail.
Experiment – data collection
Often the original theory can be verified or modified through experiments in the lab (or out in nature, depending on the case). The experimenter can keep some factors (the “parameters”) fixed, and vary some others, observing their effects on the outcome of the experiment.
Here is a well-known example of perhaps one of the first experiments through which it became understood that in order to examine scientifically the world of nature we must experiment with it. It is often said that Galileo (1564–1642) let two balls, a heavy (iron-made) and a light (wooden) one, fall from the top of the Leaning Tower of Pisa, to prove that both balls would reach the ground at the same time — contrary to then-prevailing Aristotle’s opinion, according to which heavier objects reach the ground faster than lighter ones. That Galileo performed such an experiment is only a legend. After all, even if he had performed it, the heavy ball would reach the ground faster than the light one, due to the air resistance. (Think, for example, of the extreme case in which the “light ball” is a common balloon.) For the experiment to succeed, it must be performed in the absence of air. Galileo knew that, that’s why he never performed such an experiment, but only stated the principle governing falling objects. However, the experiment was performed in 1971 on the Moon by astronaut David Scott of the Apollo 15 mission, when he dropped a hammer and a feather (see video).
Video from the Apollo 15 mission on the Moon.
Astronaut David Scott performs Galileo’s experiment.
As Scott himself — as well as millions of TV viewers — witnessed, due to the lack of air, the two objects hit the ground of the Moon simultaneously. Of course, this kind of “visual verification” is scientifically inaccurate. Scott performed the experiment on the Moon both for sensational reasons and for honoring Galileo. In its scientifically acceptable version, this experiment must be performed in the lab, in a vacuum chamber, using accurate chronometers, etc.
As mentioned earlier, in an experiment we can retain some parameters fixed and modify some other ones. For instance, in the previous experiment we can keep the altitude from which the objects fall fixed, and vary the weight of the objects. After verifying that (in vacuo) they always reach the ground simultaneously, we can keep the weight fixed and vary the altitude, wondering about the exact role of the altitude when objects fall. Subsequently, we may keep both altitude and weight fixed, and vary their shape; and so on.
It is important to note that in antiquity, and up to Galileo’s time, people usually did not perform experiments but merely stated theories, which thus remained unverified. It is impossible to know if a theory is right or wrong without verifying it experimentally. The lack of experimental verification is the main difference between ancient thinking and science as it emerged in Europe after the Medieval Times. For this reason, ancient thinkers such as the Greeks, the Arabs, etc., who studied nature are called “natural philosophers” — a sort of “pre-scientists”. Aristotle, for example, stated his opinion that women have fewer teeth than men. It would be a simple matter for him to examine the teeth of a few women (starting with his wife Pythiás, for instance) so as to reject that idea. And yet he didn’t do it, because the experimental examination of nature was not part of the ancient Greek thinking. Examining nature was the innovative idea that was introduced in Europe during the Renaissance, and led to the development of true science. And Galileo’s non-experiment acquired a legendary aura around it precisely because it was understood that that’s how one could distinguish between a right and a wrong theory: experimentally.
As another example, the geocentric model that was mentioned in an earlier section, can be verified experimentally. The experiment can be that we build a spaceship, travel into space, and verify directly whether the Earth stays at a place without moving. Naturally, an experiment like that must await for suitable technology that makes space travel possible. There was no such technology in the times of Aristarchus of Samos, who proposed the heliocentric model, nor later, in the times of Copernicus, who proposed the same model once again. In those times, people were content with how “attractive” a theory appeared to them — a matter that will be discussed later. However, even today there are theories for which we don’t have the necessary technology to verify or reject them experimentally. Such an example is the superstring theory in quantum physics, which explains the properties of subatomic particles. To verify that theory experimentally we need amounts of energy that we can’t have with present-day technology. Therefore, the superstring theory remains, at present, experimentally unverified.
Modified Theory – Publication – Criticisms
After any experiments and the collection of data, a final theory is made, which is either an improvement of the original one, or made from scratch. It’s important that the final theory must explain all observations: both the original ones (perhaps made by chance), and those that were obtained through experiment.
What remains is the writing of an article for publication (“paper”) that describes the data of the observations and the theory that explains them. The article is sent to relevant journals, or for announcement in conferences of a relevant subject. It is either accepted for publication by the editors of the journal (or by the organizers of the conference), or rejected. In reality, it is not the editors or the organizers who take the decision, but some fellow scientists, the “referees”, who read the article, and each of them issues an opinion to the editor about whether the given article is suitable for publication or not. The scientists–referees are expected to judge objectively, and in important journals they don’t know the author’s name because the editor doesn’t disclose it to them. Thus, they judge strictly according to the content, and are not influenced by the author’s prestige or authority — which will also be discussed later. Also, the author doesn’t know who the referees are, either. Thus, this procedure is called “double blind”: neither the author knows the referees, nor the referees know the author. The editor (who is usually also a scientist), after obtaining the referees’ opinion, takes a final decision about whether to publish the paper or not. Nearly always, when the decision is positive, it is not that the paper will be published unchanged, but that some changes must be made according to the suggestions of the referees. The author makes the changes within an agreed-upon deadline and re-submits the article. If the article receives a final decision of acceptance, it appears in some issue of the journal (or in the conference proceedings, when that takes place).
From there on, when the paper is published, it is subjected to the critique of the wider scientific community, since it is now available to everyone. For the critique — made through other publications — to be scientific, it must not be based on the subjective judgment of a person, but on the collection of data from new observations. If a theory makes predictions, one may test it experimentally and see if the new observations agree with the predictions. If they agree, the theory is confirmed. If they disagree, the theory is considered unsound. Thus, a new cycle starts, with new data, new (improved) theory, new publications, and so on. Naturally, there is always the question of whether the experiments were correct, so the theory is not rejected thoughtlessly with the first data that disconfirm it. However, the more data that disconfirm the theory arrive, the more the scientists’ conviction that the theory is wrong increases.
Now, regarding the question of who is the one who finally accepts or rejects a theory, the answer is that this is not a specific person, but the scientific community as a whole. The acceptance or rejection is always implicit: if the other scientists reference and make use of the results of the publication, this implies that they accept the correctness of the theory. If they make negative references or — more commonly — they do not refer to the theory at all, it is rejected. Of course, all this process includes a subjective factor: the opinion of the other scientists. But because the other scientists are many, for statistical reasons, the subjective and biased judgment of one person is inconsequential; what matters is the average opinion of the scientific community. Supposedly, scientists as a whole do not judge subjectively, being aware of the scientific method and the principles explained in the present course; that is, scientists generally judge according to the observational data, not according to their biased opinions or imagination.
| Exercise: With the above knowledge, the reader should answer the following question easily: to what extent is the lawyer a scientist? How much does he/she follow the scientific method? How many of a lawyer’s concerns and actions are related to what has been described so far? |
Critique of the Scientific Method
The reader must have noticed that the word “supposedly” was used in some places earlier in this text. The above-mentioned description of the scientific method is the ideal one. In practice there are always deficiencies — after all, how could it be otherwise? Scientists, being humans, make the same errors that all humans make.
The Bias of the Scientist Who Creates the Publication
The scientist who creates a theory is expected to judge it in an unbiased way, only according to the available data. In practice, however, the scientist often feels that the theory is his brainchild. So, just as a parent feels obliged to strive for the health and prosperity of his own children, a scientist, too, feels something analogous when defending “his” theory — especially when data from observations start accumulating that invalidate it. Looking, however, at the overall picture in science, we can say that it’s not so important if a scientist defends “his baby” against counter-evidence, because what really counts is the view of the entire scientific community, which is much more objective, because it doesn’t have a sentimental link with one person’s theory. Let’s see what the French chemist Antoine-Laurent Lavoisier (1743–1794) had to write about this, in the 18th century:
“Imagination, which drags us constantly away from reality, together with selfishness and self-assertion that know so well how to guide us, push us to conclusions that don’t follow naturally from facts, and as a result we try somehow to deceive ourselves. So, it’s not at all strange that, generally, in the sciences of nature, there appear often assumptions instead of proven conclusions [...]” “The only way to avoid such errors is to eliminate — or at least to simplify as much as we can — the reasoning that is subjective, and which by itself might mislead us; to subject it constantly to the experimental test; to keep nothing but those facts that are data of nature, and which cannot deceive us; to search for the truth in the normal succession of experiments only, and of the observations [...]” Antoine-Laurent Lavoisier, Traité élémentaire de chimie (1789). |
We’ll learn more about the above in the section on
falsifiability.
The reverse can also happen: a scientist might “fight” against a theory
developed by others, although the data seem to support that theory. An
example is the “Big Bang” theory, explaining
the initial stages of the evolution of our universe, which the
astronomer Fred Hoyle fought against up to his death, although data from
observations that supported the theory kept mounting. Actually, it was
Hoyle who came up with the term “Big Bang”, obviously as a derogatory
one, wanting to effect a “punch below the belt” to the theory. However,
his derogatory term was the one that eventually prevailed, and today the Big
Bang theory is practically the cornerstone of modern cosmology.
The Bias of the Scientists Who Judge the Publication
When an article is sent to be refereed by other co-scientists so that they decide whether it is worthy of publication or not, it happens sometimes that the article is rejected not for objective reasons, but because it disagrees with the “established view” that exists in the minds of the refereeing scientists. That is, the referees already have an opinion on which theory is correct, and instead of looking at the data objectively and allow the theory to be published so that it is judged by the greater scientific community, they don’t do that but reject the article, which is thus not published. This case is less common than the previous one, because the referees are usually three or more; however, it is not at all infrequent. Scientists often complain about this, sometimes justly, and sometimes unjustly.
Errors in Data Collection
The possibility exists, of course, that the data obtained from observations contain errors. This is something that usually does not cause much trouble, because other scientists will perform more observations that will correct the original ones. In paleontology, for instance, it happens sometimes that a not-very-accurate measurement of the age of a fossil is obtained. But by repeating the measurements, the error is eventually corrected. Here is another example, from astronomy: up until the 1990’s, the age of some stars was estimated to be older than the age of the universe! Eventually the method of estimating stellar ages was corrected, which proved the obvious: that those stars are younger than the universe itself.
Much worse than erroneous observations is the doctoring of the data on purpose, so that they appear to support the proposed theory. This is not common, because when it happens it results in the expulsion of the pseudo-scientist from the scientific community. The scientist who adulterates data is akin to the policeman who is bribed by the criminal. Doctoring the data is an act that works against one of the most fundamental notions in science, which is this one:
|
Theories are derived from
data; |
Just as with the errors that are not made on purpose, the purposeful errors will also be examined, sooner or later, by some scientists who will repeat the experiments and will face the fraud. Eventually, for statistical reasons, the wrong data (purposeful or not) are left in the margin, ignored, and replaced by the correct ones.
Errors in Coming up with a Theory
Finally, it is possible that both the data and the scientist’s attitude are correct, but the resulting theory is not right. Sooner or later, however, someone will discover the error and publish a correction. An example of that is the theory of “ether”, which appeared by the end of the 19th century. The theory of ether was proposed in order to “save” the classical physics of Newton. The latter was in conflict with observations regarding electromagnetic phenomena, and in particular regarding the speed of light in empty space. Eventually, in 1905, Einstein proposed the theory of special relativity, which abolished the theory of ether and corrected Newton’s classical physics.
In spite of the above defects of the scientific method, in general we can say that science manages to overcome its problems up to date, producing results that are objectively correct, and which usually have beneficial effects in the quality of people’s lives.
Data – Facts
Properties of the notion “scientific datum”
There are two kinds of data: data of measurement, and data of existence. (Alternatively, we can talk about facts of measurement and facts of existence. For the purposes of the present discussion, the word “datum” will be treated as synonymous with “fact”, although in a more general context the two words do not have identical meanings.)
![]() Data of measurement arise whenever it is possible to measure some
quantity and assign a value to it. E.g., we could measure various
lengths and angles on the surface of the Earth (as
Eratosthenes did, in antiquity), and then calculate the volume of
the Earth, which is a quantity expressed in some unit of measurement
(e.g., cubic kilometers).
Data of measurement arise whenever it is possible to measure some
quantity and assign a value to it. E.g., we could measure various
lengths and angles on the surface of the Earth (as
Eratosthenes did, in antiquity), and then calculate the volume of
the Earth, which is a quantity expressed in some unit of measurement
(e.g., cubic kilometers).
![]() Data of existence arise whenever we make observations from which we draw
the conclusion “X exists”, where X is either an object, or a
relation between objects, or a property of an object, or a
property of a relation. E.g., suppose we use a telescope and realize
that there are satellites near the planet Jupiter (just as
Galileo did, at the dawn of the Renaissance). Satellites are
objects. With the same observation we can see that the satellites
orbit Jupiter, and the “going around” is a relation between
objects. We can also see that each satellite has a certain brightness,
which is a property of an object. Finally, with repeated
measurements we find that the orbit of the satellite lasts for a few
days; the “orbital period” is a property of a relation. All properties also
yield data of measurement, whereas objects and relations yield strictly
data of existence.
Data of existence arise whenever we make observations from which we draw
the conclusion “X exists”, where X is either an object, or a
relation between objects, or a property of an object, or a
property of a relation. E.g., suppose we use a telescope and realize
that there are satellites near the planet Jupiter (just as
Galileo did, at the dawn of the Renaissance). Satellites are
objects. With the same observation we can see that the satellites
orbit Jupiter, and the “going around” is a relation between
objects. We can also see that each satellite has a certain brightness,
which is a property of an object. Finally, with repeated
measurements we find that the orbit of the satellite lasts for a few
days; the “orbital period” is a property of a relation. All properties also
yield data of measurement, whereas objects and relations yield strictly
data of existence.
It is wrong to imagine that something can be characterized either as “a fact” (giving us data), or as “not a fact” (“a theory”), using a black-or-white logic. There are gradations to how much some piece of information can be considered as a fact. Some examples will clarify this idea immediately.
![]() Let’s start with an example that appears to give us undoubtedly a “datum
of measurement”: suppose we are asked to determine the temperature in a
bucket full of water. Therefore, simply, we dip a common thermometer in
the water and, provided that the water is not so hot that its
temperature exceeds the maximum indication on the thermometer, we simply
read the temperature. Suppose that it says: 25°C. Is that a “datum”? Do
we now know it as a fact that the water has a temperature of 25°C?
Let’s start with an example that appears to give us undoubtedly a “datum
of measurement”: suppose we are asked to determine the temperature in a
bucket full of water. Therefore, simply, we dip a common thermometer in
the water and, provided that the water is not so hot that its
temperature exceeds the maximum indication on the thermometer, we simply
read the temperature. Suppose that it says: 25°C. Is that a “datum”? Do
we now know it as a fact that the water has a temperature of 25°C?

First of all, our thermometer might be faulty. But we can take care of that issue by examining the thermometer before the experiment, comparing it with other, similar ones. So we perform the experiment only after making sure that our thermometer is not obviously faulty but behaves like all the other ones.
But there is still a problem: it is impossible that all thermometers are absolutely identical and give exactly the same readings. This happens because due to tiny errors and microscopic differences in their construction (which might require a magnifying lens to be seen) they are bound to have slight deviations in their readings. So, why should we trust the thermometer that we selected among several similar ones and not another one of them? Also, the temperature is slightly different in different regions of the water, because the bucket is warmed up and cools down unevenly on each side (e.g., depending on the direction of the source of light in the room), creating tiny currents in the water that slowly carry the different temperatures around, yielding an inhomogeneous temperature if we insist to have a sufficiently precise level of accuracy.
But that problem, too, can be countered easily: let’s insert not just one, but 10, or 100 thermometers in the water of the bucket. So we collect the readings of all the thermometers (25.1°C, 24.8°C, 25.2°C,... etc.), that is, we collect a statistical sample, and thus obtain not a single value but a statistical average. E.g., the average of the temperatures of our sample might be 25.073°C. Indeed, by using very simple methods of statistics, we can say that, according to our sample, the temperature of the water is between 24.7°C and 25.3°C with a certainty of 95%. If we want to increase our certainty, the range of possible values will increase correspondingly. (E.g., with a 99% certainty the average temperature might be between 24.6°C and 25.4°C, values that are computed by the same statistical formulas.)
Thus, a datum that results from measurement should never be a plain number, but a statistical description, accompanied by a degree of certainty. As we conclude from the above, the degree of certainty can never be perfect, that is, 100%.
![]() We
proceed now to “facts of existence”, which will concern us a little
more. A very simple example is the following: is it a fact that the
Parthenon of Athens exists?
We
proceed now to “facts of existence”, which will concern us a little
more. A very simple example is the following: is it a fact that the
Parthenon of Athens exists?

The Parthenon
If we happen to live in the city of Athens, it is extremely easy to verify the truth of this fact with our own eyes, since a short walk in the city is sufficient. (The Parthenon, on top of the rock of the Acropolis, can be seen from many locations of Athens, because the city is built in such a way so as to facilitate its view.) And if we don’t live in Athens, then a trip to Athens suffices for us to verify the existence of the ancient monument with our own eyes and accept it as a fact that “the Parthenon exists”; therefore, also that the books (and web pages, TV images, etc.) that show it are not part of a great conspiracy that tries to present to us as existent something that in reality does not exist. The question of how many troubles, sacrifices, and expenses we are willing to accept depends on where we are on the planet and how strongly we wish to verify the fact. If, for instance, we live in Australia, we must go through a lot of trouble (and expenses, etc.); but, in any case, we are in principle in a position to determine the truth of the existence of the Parthenon using our own eyes.
However, it is worth noting that when we see an object with our own eyes and wonder about whether it exists, the certainty with which we answer “Yes” cannot be exactly 100%. For instance, there are people who feel the existence of supernatural entities around them. Of course, Parthenon is not supernatural, but entirely natural. But still, there are people who see entirely natural objects in front of them (see course N4, and in particular the “Charles Bonnet Syndrome”), and those people are entirely normal. We could be one of them. We know, of course, that chances are that we are not one of them, but one cannot be absolutely sure. Thus, our degree of certainty should not be exactly 100%, not even for objects that lie right in front of our very eyes.
![]() Now
let’s make the question of existence of an object slightly more
difficult: does the planet
Neptune exist?
Now
let’s make the question of existence of an object slightly more
difficult: does the planet
Neptune exist?

Neptune
To answer this question we cannot rely on a stroll in the city, nor on a trip by car or plane. We must equip ourselves (1) technologically (with a telescope or strong binoculars) and (2) with technical knowledge, so that we know at which location on the sky and at which time of the night to look for Neptune. But this question, too, is not beyond the abilities of the average person who wants to see Neptune with their own eyes; neither the telescope or strong binoculars cost a lot, nor is it too difficult to obtain the information of where to look at and when (e.g., through the Internet). So, the same remarks hold here, too, as those that were made for the case of the Parthenon.
![]() However, the moment technology is required to verify the existence of an
object, it becomes evident that the question of existence might be such
that its answer exceeds the ability of the average person to verify it
with their own eyes, even if willing to undergo sacrifices and make
expenses. For example: does the satellite
Sao
of Neptune exist?
However, the moment technology is required to verify the existence of an
object, it becomes evident that the question of existence might be such
that its answer exceeds the ability of the average person to verify it
with their own eyes, even if willing to undergo sacrifices and make
expenses. For example: does the satellite
Sao
of Neptune exist?
Artistic drawing of Sao (not a real picture)
Only very few people in the world can answer that question by using their own eyes, because Sao of Neptune is a minute satellite of an already very faraway planet. It took the spaceship Voyager-2 and its approach to the vicinity of Neptune in 1989 to discover six of the planet’s satellites (not yet Sao among them), in addition to the then-known two satellites; whereas Sao was discovered in 2002 by an American team of astronomers. The “mere mortal” has hardly any chance to see the tiny Sao, ever.
Therefore, there are “facts” (indeed, an extremely large number of them) for which we cannot rely on our personal observations to determine whether we accept them as facts or not. We must rely on observations of other people: those who have the technical means to make them. For this reason, our degree of certainty for the existence of Sao must be smaller than the corresponding degree for the existence of the Parthenon or Neptune. But what kind of observations can we accept? Do all observations “count” as scientific ones? And who are the people whom we can trust for accepting data from observations that they made? How can we know that they don’t try to deceive us, or that they are not self-deceived, after all?
Criteria for Acceptance of Observations: Which Observations Generate Scientific Data
Since data that are obtained from observations play a fundamental role in the scientific method, it’s natural to require to know what kind of observations yield scientific data. As a motivation for thought, consider the following examples:
-
Suppose I am alone in a dark forest, away from all other people. Suddenly, I hear a voice whispering to my ear: “Watch out!” I look around and make sure there is no one near me. Is this an observation? Is it a fact that someone whispered to my ear?
-
An ancient inscription of a people who disappeared 1,000 years ago writes that all the members of the tribe (which, we conclude, numbered more than 1,000 individuals) witnessed a gigantic spider descending from the sky and landing on a nearby hill. Is this an observation?
-
The members of a small religious community who live isolated in a desert claim that their leader has repeatedly done miracles, healing the sick, and even resurrecting the dead. Does that count as an observation?
-
The monks in a monastery make similar claims regarding healing (but not resurrection) which they attribute to the miraculous action of a religious icon (a painting). Could that be considered data from observation?
-
The members of a religion that includes over a billion faithful people claim that, according to their holy book, the founder of their religion walked on the surface of the water. Members of a different religion, also with over a billion people, claim that their holy book is the direct word of their god, given to the founder of their religion when he was alone in a cave. Can we consider those claims “facts” that resulted from observations?
-
The residents of a present-day town with a size of over 20,000 people claim that they saw fires crossing the sky on a specific day and at a specific time. Could that count as observation?
The sections that follow will help us answer the above questions.
To each observation we assign a degree of certainty, according to how much we believe that the observation reflects reality or not. That is, the observation is not assigned one of merely two values, “right” or “wrong”, but a degree of certainty based on four criteria that are discussed immediately below: verifiability, objectivity, independence, and multitude of observations. The degree of certainty is the probability that the observation is correct, i.e., that it’s a “fact” and we can use it to obtain “data”. It can be nearly 0, if we are almost certain that the observation is wrong; or it can be nearly 1, if we are almost certain that it’s correct; or it can have any value in-between 0 and 1, but not including those two values. The closer the degree of certainty is to 1, the more comfortable we feel in calling it a “fact”, yielding scientific data. Therefore, we don’t simply accept or reject the data from an observation, but we say that some observations are more worthy of yielding scientific data than some other ones. So, here are the criteria that should be used to assign a degree of certainty to each observation.
Verifiability
Perhaps the most essential feature for an observation to be characterized as scientific is that it must be verifiable. That is, it must be possible for other observers to repeat the observation, after it has been announced that the observation was made (or simultaneously, if it is an expected, world-wide observable event, such as an astronomical phenomenon).
This requirement immediately rejects the case of the whisper in the forest, because no one is in a position to verify that person’s experience. Notice that not even the person themselves can verify it, because they cannot repeat it. Hence, no matter how certain they are that they heard a whisper or a voice, their experience is not verifiable, therefore not scientific either. The certainty of the person themselves is of no import, because by studying, e.g., neuroscience, we learn that there is a region in the brain that assigns to our own self the voice that we “hear” when we think explicit thoughts, or when we read something. I.e., when that region of the brain works normally, we know that that voice is ours; but when, for various reasons, that region “turns off” (i.e., stops working as usual and does not process its signals), as it can happen on some rare occasions, then we hear our internal voice as if it was produced not by ourselves but by the external world. Exactly the same is true for visual information: one might literally see an object, a figure, an “entity”, that looks totally real to the observer, and yet is the product of that person’s brain that works under special conditions (e.g., anxiety, stress, tiredness, hunger, etc.); it happens when a center of the brain turns off, which allows us to know when what we see belongs to the external world and when it is a product of our imagination. (Such issues are examined in detail in course N4.) In any case, that is an explanation of the phenomenon; irrespective of whether an explanation exists, the observation is not scientific, being non-verifiable.
The requirement that the observation be verified might give the impression that a large number of events that happened in the past and cannot happen again in the future are termed “non-scientific”. For instance, is our knowledge about fossils non-scientific, since each fossil was made once in the past and, by its nature, cannot be made again? The answer is that if we are interested, e.g., in the age of the fossil, then whoever wishes (and knows how to do it) is free to estimate the age of the fossil as many times as they want. (In course B1 we learn how the ages of fossils are estimated.) Therefore, the datum in this case is not “the fossil”, but the shape, color, weight, etc., and an estimated age of a stone. Those are definitely scientific data, since they are all verifiable. What is not verifiable is the evolution from species A to species B. Hence, the biological evolution of a species into another is not a fact (unless it concerns bacteria or viruses, which can be observed in the lab), but a theory that explains the data (of fossils, differences in DNA, etc). What some scientists mean when they say “evolution is a fact” is that, given the overwhelming evidence that is available to everyone who studies biology, the degree of certainty that the theory of evolution is correct is so high that the notion of evolution stands rather near the “facts” end of the spectrum, instead of near the “theories” end. This idea will become clearer when we consider theories in more detail.
What can we say about historical events, such as the Holocaust? Taking into account all the criteria described in this section (and not only verifiability) we can obtain a degree of certainty for historical events. For the said certainty other criteria are useful, such as the multiplicity of sources, how much we can trust them, etc. (see below). The Holocaust has been documented by so many sources, and so objectively, that we can be almost absolutely certain that it happened (perhaps as certain as that the 2nd World War happened). But other historical events, such as the “Armenian Genocide” (of 1915) are disputed by some (e.g., Turks) and supported by most others. One may obtain a degree of certainty by examining the historical sources and documents that exist. Thus, history is a scientific field to the degree that it is concerned with the objective examination of data (see next subsection), and results in theories that interpret the data and attempt to predict the future.
Objectivity
Another crucial requirement is that the observer be objective. To see why, it suffices to consider a very well-known situation: suppose we ask the believer of a religion X about whether religion Y is correct or not. Independently of whether religion X is right or wrong, the believer of religion X will reject religion Y, stating that it is false. (Otherwise the believer of X should convert to religion Y.) Thus, this example shows that, deep down, the lack of objectivity is strongly related to the problem that we examined already: putting opinions ahead of observations and data. Being objective implies looking at the evidence impartially, and drawing conclusions only from the evidence, and not because of what one wants to be true.
Objectivity is also a requirement of extremely high importance, just as verifiability. The lack of objectivity essentially circumvents the purpose of observation, which is to record what really is going on in the world, avoiding the observer’s personal opinions and biases. In practice, it can happen that a scientist is not objective, especially when what is disputed is a product of the scientist’s work. However, as already mentioned, the scientific community in its entirety suffers much less from this problem. Consequently, when we deal with theories that are judged as correct by the overwhelming majority of scientists — such as the theory of relativity, the theory of evolution by natural selection, the theory of the movement of tectonic plates, etc. — then we can be quite confident that the assessment of the entire scientific community is objective.
Sometimes it is wrongly claimed — exclusively by people who never participated in scientific research, and who are unaware of the scientific method — that scientists as a whole are not objective, that they have a secret agenda, or that they see things with their own, “scientific opinion”, which is only one of many available approaches to reality. Indeed, the scientific is only one of the available approaches; but we should note that it is probably the best possible, the most successful approach, judging from technology — the “fruit” of science — and the thousands of ways in which technology improves people’s lives. It’s not a coincidence, after all, that when an assertion of validity of an idea must be made, what is usually claimed (if possible) is that “It is scientifically proven...”; nobody ever claims that something, e.g., “is astrologically proven”.
Independence
The importance of observations is greater when the observations are done independently.
Example: In one case, three people who had a picnic together out in the country claim that they saw a flying saucer crossing the sky. In another case, three people, unknown to each other, and living at three different parts in the countryside and far away from each other, claim that they saw the same phenomenon: a flying saucer crossing the sky. In the second case the observation is of greater importance, provided that it is determined with sufficient certainty that the three observers were indeed unknown to each other.
However, in the previous example, in none of the two cases do we have a scientific observation, because the reported event is not verifiable; unless pictures of the event or a video was taken, in which case such material must be examined for its authenticity.
Here is an example taken from the scientific reality, showing the importance of the independence of observations. There are two ways to estimate when the most recent common ancestor of all living people lived. One way is by examining the age of fossils of individuals that have the same skeletal characteristics as those of our species, Homo sapiens. The said age is estimated using methods of quantum physics (measuring the remaining percent of the radioactive isotopes of some elements), and is found to be somewhere between 150,000 and 200,000 years ago. Recently (in the last few decades), another method has been developed: the “molecular clock”. This means examining the DNA of a representative sample of people who are alive today, and subsequently “moving backwards in time”, using the notion of the rate by which mutations appear in the DNA molecule, and figuring out the time at which all the DNA molecules of the sample would become practically identical, converging to the DNA of the common ancestor of all members of the sample. This method, too, gives us an age that is very similar to the age found by the method of the fossils: again between 150,000 and 200,000 years ago. Because the two methods are entirely independent of each other, and because they end up with the same conclusion, we have a much greater certainty about that conclusion than we would have if we knew and applied only one of the two methods.
Multitude
The number of observations also plays some role in how much we can rely on them. In the example of the previous subsection (seeing a “flying saucer”) the importance of three persons observing the phenomenon is less than the importance of the observation of the same phenomenon by almost all the adults of a little town, numbering 20,000 people. However, itself alone the large number of observations is insufficient to characterize something as a fact, because there are well-known examples of cases in which almost the entire humanity thought that something is a fact because that’s what was obvious by direct observation, and yet, the “fact” was wrong. For instance, in antiquity, almost all people thought that the Earth is flat, because that’s what their eyes were telling them. Also, they were seeing the heavenly bodies cruising across the dome of the sky, and thought that the Earth stays immobile at the center of the universe, whereas all the heavenly bodies revolve around it. However, not only is this not true, but even “the dome of the sky” does not exist — it is an optical illusion. Therefore, the number of observations and observers is important, but we cannot rely exclusively on that (no matter how large it is) to determine whether we have a scientific fact.
In the previous example (the one of estimating the age of our most recent common ancestor, e.g., through the “molecular clock” of the DNA), the larger the number of people in the sample is (those whose DNA is examined), the more secure and accurate the conclusion we reach is, regarding the estimated age.
|
Exercise: Based on the above, try to answer, one by one, the examples that were listed at the beginning of this section. Your answers should not be a simple “Yes, it’s a fact” or “No, that’s not a fact”, but you should feel that you have an approximate degree of certainty with which you could accept the claim as factual. |
Presumed “Data” that, in Reality, Are Theories
In the next section we shall examine in detail the notion of “theory”. But, already at this point, we should note that, in some scientific fields, it is assumed that there exist some “objects” (or relations among objects) that no one has ever seen with their own eyes, either because the required technology does not exist yet, or because we are restricted by the way human vision works (which means that we don’t have any hope to see those objects ever, irrespective of the technology). And yet, we admit that such objects “exist”, because in that way we can explain (up to some degree of certainty — sometimes very high) other observations, made on other objects. We should understand that the “objects” that have not yet been observed directly can also be seen as theories; but they are theories that no scientist can reject; after all, there is nothing better with which to replace them. Let’s see some examples.
![]() Subatomic particles:
Subatomic particles:

Drawings of models of an atom (left) and of a proton (right).
Only rough depictions can be given, and such depictions necessarily are
far from reality.
No one will ever see directly an electron, quark, gluon, neutrino, or any other of the subatomic particles that constitute matter. The reason is that when we see an object we do so because one or more photons are emitted by that object and are detected by the retina of the eye (where they activate some light-sensitive cells: the “cones” and the “rods”). But when the object that we want to see is as tiny as a subatomic particle, then the photon is too coarse as an instrument in order to see the particle. When an electron emits a photon, the properties of the electron (e.g., its momentum, location in space, etc.) change. As a result, the photon that the eye detects does not give us correct information about the present state of the electron. In other words, visual observation (which uses photons) influences the observed object (the subatomic particle). To be able to really see something it must be that that something has sufficiently large mass so that it is not influenced substantially by photons. Therefore, since we can see only through photons, we have no hope ever of seeing a subatomic particle, the existence of which can only be inferred indirectly: firstly because it explains effectively a large number of other facts and observations (among which is the correct functioning of TV’s, computers, cell phones, GPS’s, and a host of other high-technology products), and secondly because it follows as a solution of equations of quantum physics. The other “data that are actually theories”, which are discussed below, also have this characteristic: they are obtained as solutions of equations.
![]() Black holes:
Black holes:

Computer simulation of the appearance of a black hole
No one has seen directly a black hole in space because — being black — the hole can be seen only against the background of a bright nebula instead of the usual (and also black) background of interstellar space. In addition, the black hole has by its nature extremely small size; e.g., a diameter of only a few kilometers. Thus, no black hole has been seen directly to date. But there are other observations that indirectly imply the existence of a black hole, such as a strong source of X-rays (due to nearby matter that is “swallowed” by the black hole, and which matter emits X-rays when it approaches the so-called “event horizon” of the hole), or the orbiting of a star around an invisible but massive object (the assumed black hole). But those are the direct observations — the facts that are explained best by the theory that there exists a black hole at that location in space. We should also mention that black holes are not arbitrary inventions of imaginative scientists, but are described by solutions of equations of the theory of general relativity.
![]() Gravitons: The “gravitons” are the supposed carriers of the force of
gravity. That is, it is assumed that when two material bodies attract
each other, they do so because they exchange gravitons. Gravitons, too,
are inferred as solutions of quantum-physics equations, but their
existence has not been verified yet. And that is quite expected, because
in order to have any hope to detect a graviton we should construct a
detecting device of the size of planet Jupiter (the largest planet of
our solar system), place the device to a close orbit around a neutron
star (a relatively rare type of star that has extremely large density),
and even then, we could hope that this monstrous device would detect
just a single graviton once in ten years, if it was detected (source).
Because it is technically impossible to implement such a
science-fictional scenario, we must hypothesize the existence of
gravitons only because they are solutions of some equations. We should
note that, in this case, we don’t even have the indirect data that could
be explained by the existence of gravitons (although attempts are being
made with exactly that purpose). Therefore, at present the “graviton”
looks more like theory rather than fact.
Gravitons: The “gravitons” are the supposed carriers of the force of
gravity. That is, it is assumed that when two material bodies attract
each other, they do so because they exchange gravitons. Gravitons, too,
are inferred as solutions of quantum-physics equations, but their
existence has not been verified yet. And that is quite expected, because
in order to have any hope to detect a graviton we should construct a
detecting device of the size of planet Jupiter (the largest planet of
our solar system), place the device to a close orbit around a neutron
star (a relatively rare type of star that has extremely large density),
and even then, we could hope that this monstrous device would detect
just a single graviton once in ten years, if it was detected (source).
Because it is technically impossible to implement such a
science-fictional scenario, we must hypothesize the existence of
gravitons only because they are solutions of some equations. We should
note that, in this case, we don’t even have the indirect data that could
be explained by the existence of gravitons (although attempts are being
made with exactly that purpose). Therefore, at present the “graviton”
looks more like theory rather than fact.
The above examples tell us that there is no clear separation between “fact” and “theory”. There is a “gray area” in which the two notions overlap and can be confused. In reality there is a continuous range, one end of which we call “facts”, and the other end we call “theories”. For each member of the continuous range we only have a degree of certainty that “it exists” or “is true”. For some members (e.g., the “existence of the Parthenon”) we have extremely strong certainty and we do not hesitate to call them “facts”; for other members we have less strong certainty, so we prefer to call them “theories”; but there is nothing that sharply distinguishes fact from theory.
But let’s see now what properties we demand from those that call “scientific theories”.
Theories
If all we were interested in was observation and data collection, today’s science would be nonexistent; instead, we would be at a primitive, pre-scientific stage. For example, the numbers 7, 14, 21, 28, 35, and 42, by themselves alone are useless, they can’t help us in anything. The important next step is to notice that they are “the multiples of 7”; that is, to state this “theory”, or “hypothesis”, so that we are in a position to predict which number comes next. This, after all, is one of the major goals of science: to predict the future. When, for instance, meteorologists predict tomorrow’s weather, they are not content with a mere recording of the data sent by the satellite, but have fed those numbers into some meteorological model (the “theory”), which produces a prediction as a result.
But when do we say that we have a scientific theory? One might claim, for example, that according to our observations on how the world of nature is organized it follows that some Supreme Power must have created it. Is that theory scientifically acceptable?
Falsifiability
The most important property that a theory must have so that it can be called “scientific” is that it must be falsifiable.
Example: suppose that, given the numbers 7, 14, 21, 28, 35, and 42, we state the theory: “those are the multiples of 7”, and so we predict that the next number should be 49; then we have a falsifiable, and therefore a scientific theory. “Falsifiable” means: “possible to be shown false”, depending on the data that will be observed later. For example, if the next number turns out not to be 49, then our theory will have been falsified, and we should change it so that the new theory includes both the old numbers and the new one, which was unexpected according to the old theory. E.g., if the next number happens to be 50, here is a new and improved theory: “The numbers are the first six multiples of 7, and from there on we must add 1 on each next multiple of 7.” (Notice that although this theory might sound a bit complicated, a mathematician can easily write a formula that denotes it in a few math operations.)
What happens if no new number (no new datum) can be obtained? Then our theory cannot be falsified because, although it makes a prediction (that the next number will be 49), since there is never going to be a next number, no one will ever be able to show that this theory is false (to falsify it), therefore to examine whether it is correct or not. It could be, for instance, that the given numbers (7, 14, 21, 28, 35, and 42) were created by some other, more complex method than the multiples of 7, a fact that we will never know, since no new datum will be produced. In this case, if we cannot examine in detail the method by which the numbers were produced, we cease having a theory; instead, we have a datum: those six numbers — and nothing else. But if we can examine the method (e.g., a computer program that calculated and produced those six numbers, one by one), then again we have no theory, but a clear understanding of the deeper mechanism responsible for the data.
Let’s proceed now to a more realistic example. Suppose we observe the kinds of swans that exist in the world; and that we are still in the year 1600, when America has already been discovered, but Australia remains unknown to all but its native inhabitants. All swans that have been observed in all the known places of the world (including North and South America) are white.
 |
 |
 |
 |
| Cygnus buccinator | Cygnus olor | Cygnus melanocorypha | Coscoroba coscoroba |
Examples of kinds of white swans, from Europe, America (North and South), and Asia.
So we form the theory: “Swans are always white” — a theory that agrees with all the so-far known data. Our theory is falsifiable, because if a non-white swan is ever found, the theory will have been falsified. Indeed, after the discovery of Australia, we observe that there exists the kind of black swan Cygnus atratus; therefore, our theory has been falsified (and so it is false).

The species of black swan of Australia, Cygnus atratus
It is important to differentiate the notion “falsifiable” from the notions “false/true”. A theory can be true, and still remain falsifiable. (It should always remain falsifiable for it to be scientific.) For example, if even the swans of Australia were white, the theory about white-only swans would be correct, but would remain falsifiable, because we might find some thitherto unknown environment on Earth where swans were non-white. Now, if we have searched every nook and cranny of our planet (and are absolutely certain that there is not a single place that escaped our attention), and didn’t find any swans of a color other than white, then we do not have a theory anymore, but a datum: “All swans are white”.
As long as new data arrive that keep supporting the theory, that is, not falsifying it, our certainty that the theory is correct keeps rising. However, our certainty never becomes exactly equal to 100%, unless we know there will be no more data, as in the hypothetical example with the swans.
Let’s extend the above thought, bringing it to its extreme but logical conclusion. We know that when we let go of an object from some height the object falls toward the surface of the Earth. We have a theory for this phenomenon: it is the theory of gravity, which was part of Newton’s classical mechanics, and now is part of Einstein’s theory of relativity. No matter how many times we have let go of an object, it has always fallen downwards in an accelerating motion, always according to the theory of gravity. We never observed an object moving upwards or following a different direction. (Of course we think of objects that are heavier than the air; objects like hot-air balloons or balloons filled with helium also move according to the theory of gravity, since it is the heavier air that “falls” around them.) What does that mean? That the theory of gravity has been fully verified and is absolutely true? Is it falsifiable or not?
No, definitely the theory has not been 100% verified, and of course is falsifiable. The theory predicts that the next time we let go of an object heavier than the air, the object will move accelerating downward. But if we ever see, even once, that kind of motion not to happen — and assuming we make sure we weren’t tricked, falling victims of a magician’s tricks, hypnotism, etc. — the current theory of gravity will have been falsified, in which case we must augment it, so that the new theory includes the new observation. Admittedly, this is an extreme example, because objects fall millions of times on Earth daily, and nobody ever complained that one of them went upward and was lost in space. Therefore, we have a corresponding certainty that approaches the value of 100%. But it must never be exactly 100%.
|
Exercise:
The
reader can try to imagine a new law of gravity, which
should be compatible with all the observations made to this
date; that is, the new law should explain why all objects
that we observe daily move toward the center of the Earth
(or of the planet, in general), but the new law must predict
some observations that, if made, would falsify the present
theory of gravity. Needless to say, the new law must be
compatible with all the rest of the natural laws; that is, no
recourse to supernatural powers should be made. |
Let’s move on to the theory of evolution. One might observe that the theory of evolution concerns events that happened in the past. It is a theory entirely about the past, therefore it makes no predictions about the future that can be tested, at least within reasonable time and not millions of years later; therefore it is not falsifiable; hence not even scientific. Is that thought correct?
No, it is wrong. The theory of evolution indeed makes testable predictions. For example, it predicts that we will never find the fossil of a mammal dated more than 400 million years ago (because that long ago animals had not yet evolved into mammals); we will never find a fossil of our own species (Homo sapiens) dated more than 1 million years ago; and so on. The moment we find a fossil with an age that can’t be explained by the evolutionary theory (and after making repeated assessments of the age of the fossil, so that we rule out the case of a measurement error), we will have falsified the theory of evolution, which must then be corrected so that it accommodates the new datum. The biological theory of evolution, making thousands of predictions like those mentioned above, is clearly falsifiable, hence also scientific. Simply, it has not been possible to falsify it to this date.
But what about the so-called “theory of Intelligent Design”? That theory claims, more-or-less, that although living beings might have changed and keep changing to a small degree, an Intelligent Designer intervened at some crucial moments in time, a Designer who created the most complex of the organs (e.g., the eyes), and without whom we wouldn’t exist today. Is that theory falsifiable?
If we think about it carefully, we’ll see that it is not. Whoever disagrees is free to propose a prediction that this theory makes, which we should be able to falsify through observation, even if in the end we fail to falsify it. We should be given the opportunity, however. The theory of Intelligent Design provides no opportunity for falsification of a prediction — because it makes no predictions. Note: pointing to another organ that appears complex enough (e.g., the ear) does not constitute a prediction, but merely a suggestion of an object about which the person who suggested it ignores the way it could have evolved. The personal ignorance of an event does not imply that the event happened by means of a miracle (i.e., by circumventing the laws of physics). In reality, whenever someone claims that something happened by means of a miracle, that person prevents the falsification of such a claim. Why? Because the Being who caused the supposed miracle could very well take precautions so that any attempt at falsification will fail. Therefore, any theory that invokes some higher and supernatural intelligence that has the power and ability to circumvent the scientific checking, is necessarily not scientific.
Also, it is important to understand that the burden of figuring out how a theory can be falsified rests on the shoulders of the person who proposes the theory. For example, whoever proposes the theory of “Intelligent Design” to explain how living beings appeared on Earth must also suggest some way by which that theory can be falsified, if the claim is that the theory is scientific. Otherwise — if there is no way by which the theory can be falsified — we don’t have a scientific theory but merely an opinion. (For the reader’s edification: there has never been proposed a method by which the “Intelligent Design” theory could be falsified.)
About the Wrong Tendency to Support, Rather than Falsify
In psychology, it is well known that people tend to seek the confirmation of their views (or of their scientific theories) rather than their falsification. This tendency and practice is totally wrong, because no matter how many confirmations we have, we can only obtain an approximate degree of certainty for the truth of a view; whereas, in contrast, a single falsification suffices to assure us immediately of the error. Therefore, the scientist who wants to be honest (but also the non-scientist who wants to have an honest opinion on something) must seek primarily the falsification.
Interestingly, the English philosopher Francis Bacon (1561–1626) wrote on this issue already since the 17th century (the last sentence was emphasized by the author of the present notes):
“The human understanding when it has once adopted an opinion (either as being the received opinion or as being agreeable to itself) draws all things else to support and agree with it. And though there be a greater number and weight of instances to be found on the other side, yet these it either neglects and despises, or else by some distinction sets aside and rejects, in order that by this great and pernicious predetermination the authority of its former conclusions may remain inviolate. [...]” “And such is the way of all superstition, whether in astrology, dreams, omens, divine judgments, or the like; wherein men, having a delight in such vanities, mark the events where they are fulfilled, but where they fail, though this happen much oftener, neglect and pass them by. But with far more subtlety does this mischief insinuate itself into philosophy and the sciences; in which the first conclusion colors and brings into conformity with itself all that come after, though far sounder and better. Besides, independently of that delight and vanity which I have described, it is the peculiar and perpetual error of the human intellect to be more moved and excited by affirmatives than by negatives; whereas it ought properly to hold itself indifferently disposed toward both alike. Indeed, in the establishment of any true axiom, the negative instance is the more forcible of the two.” Francis Bacon, 1620: Novum Organum, Book 1, XLVI. |
Authority of Scientists
Normally, it is assumed that the authority of a scientist plays absolutely no role on whether a theory should be accepted or not. In other words, it is of no import who someone is, but what one claims. This is important as a rule, because it rejects authority as a source of truth and information. Let us recall that religions rely primarily on authority so as to accept something as true. (E.g.: «Since Prophet [X] said this, it must be true.») In science, it is not the person who makes a claim that is important, but the data. The question is always whether the data support the claim. Data take priority, opinions follow.
In practice, however, opinions of scientists with prestige are given more attention than those of others who are unknown. Truth, of course, is not determined on the basis of authority, but what happens is that more attention is paid when some idea is stated by a well-known scientist. This is because it is tacitly assumed that the scientist did not acquire prestige arbitrarily and for no reason, but due to the abilities that the scientist already displayed. That the scientist has prestige means that his or her views became accepted as scientifically valid; therefore there is an increased probability that the new views will also prove correct. The point is that the well-trained scientist knows how to draw valid conclusions, and the increased probability that this will happen again is tacitly admitted by the rest of the scientific community. However, this is merely a matter of probabilities for opinions to be correct, not a matter of uncritically accepting opinions due to the scientist’s authority.
Ad Hominem Attacks
One issue that’s related to the authority of scientists is the ad hominem attacks. “Ad hominem” is Latin for “to man”, meaning in this case: “against the person”. This expression is used when, instead of someone supporting arguments by data and logic, one attacks the character of the person who expressed a theory or opinion. A typical example of ad hominem attacks is the effort to denigrate Charles Darwin’s name in order to undermine the theory of evolution. So it is sometimes said that Darwin, supposedly, renounced the theory of evolution toward the end of his life. Nothing like that happened, but even if it had happened, it would be irrelevant to the correctness or falsity of the evolutionary theory. Such attacks are usually made by people who lack an integral education in science, and so they do not understand that the personal opinion of scientist X who proposed a theory is irrelevant. Having been used to the idea of “truth by authority” in other, non-scientific domains, such people think that the same idea applies in science. In reality, the moment an idea, opinion, or theory is stated in public, it ceases to belong to the person who stated it; instead, it belongs to humanity as a whole. Other people are in a position to test whether it is true or not, irrespective of what the original proponent of the theory now believes.
Verification of Claims through References
A scientist who writes a paper and plans to submit it for publication must support every claim through references to earlier publications (either of others, or of the same author). Even if the scientist is sure about the correctness of the claims, references must still be given for two reasons:
-
it could be that, in spite of the author’s certainty, the claims are wrong; or
-
it could be that the reader is not certain about those claims
This last point is important, because one can never know what the reader knows; thus, one should give to the reader the opportunity to examine the sources of the claims, so that every doubt is eliminated. In addition, by referring the reader to prior sources, the author ceases to be responsible for those claims; the parties responsible for their correctness are then the authors of the source publications, and all those who accepted and published the sources. Of course, if a source publication is in error, it follows that any article that uses it is equally in error. Therefore, scientists should not reference sources indiscriminately, but carefully select the publications that support their own articles.
Why the Scientist is a Skeptic
Suppose that we learn that during a meeting of some people in a house someone among them made an exhibition of “psychic powers” (without claiming to be merely a magician), either by bending spoons “by the power of the spirit”, or by making objects be raised from the ground and staying still in mid-air, again by the same “power”.
Why do scientists take such claims with a lot of skepticism?
That’s because the scientist — especially the physicist — knows which forces exist in nature. They are exactly four: electromagnetism, weak nuclear, strong nuclear, and gravity. Those are the only forces or “powers” in nature known so far, and of course no supposed “psychic power” is included among them.
We talked, however, about “powers [...] known so far”. What if there is indeed a hitherto unknown “psychic power”?
Here, the scientist’s reasoning (which is subconscious and creates the skepticism) is as follows: “Is it ever possible that millions of scientists throughout the world, including Nobel laureates in physics, and others who have been among the most intelligent people that ever walked on earth — including such luminaries as Einstein, Bohr, Heisenberg, Feynman, Hawking, and so many others — is it at all possible that they are all in error thinking that the forces of nature are the ones known in physics, whereas person X who claims to possess an unknown ‘psychic power’ is right?” Definitely, the supposed “psychic power”, if it existed, would also be a force of nature, since it makes physical objects move; therefore it could be examined in the physics lab. However, no physicist has ever observed such a force. Thus, the scientist’s subconscious reasoning is that it is highly unlikely that all physicists and the smartest people on earth are all wrong, but person X is right claiming to have some so-far unknown “psychic power”. After all, if X had indeed such a power, he or she could establish a new and unexplored area of physics, earning great fame, a Nobel award, and a lot of money. Therefore, such claims sound extremely “fishy” in the scientist’s mind.
An example of a person who claims to have just such supernatural powers is the well-known “psychic” Uri Geller. In the video clip that follows, commented by James Randi, a Canadian-American stage-magician, skeptic, and investigator of paranormal claims, we see Geller as a guest in Johnny Carson’s “The Tonight Show”. Johnny Carson (1925–2005), a comedian who once was himself a magician, thought that Geller was a mere impostor. So, Carson called Randi before the studio recording of the show, and asked him for advice. Following Randi’s advice, Carson and his crew at the studio prepared a collection of little bottles, all closed airtight, which we see on the table in front of Geller. One of the bottles had water in it, whereas the rest were empty. Geller simply had to guess which bottle had the water, an achievement he had demonstrated many times until then (but always using his own bottles, and of course according to his own terms of performing the show). Let’s see that event, with Carson hosting Geller:
|
|
Note: for subtitles in Arabic, after starting the video, click on the red button labeled ← CC |
The previous example regarding “psychic powers” can be generalized to any similar claim. Every claim about something that opposes the laws of nature, in reality opposes a gigantic edifice. The non-scientist has a hard time appreciating how gigantic this edifice — and therefore how hard its demolition — is. That’s why non-specialists are much easier to accept claims about paranormal phenomena. On the contrary, the specialist in science understands that whoever claims to have violated the known laws of physics does the analogous thing with a person who claims to have demolished with a kick a building that stood in front of him, without that person realizing that the supposedly demolished building has the size of a skyscraper, and that buildings of such sizes are impossible to demolish by the muscular power of a single human being anymore.
The Fundamental Assumption Regarding the Scope of Science
The previous discussion on the existence of “psychic powers” that move objects leads us to an additional important idea:
|
Anything that is in a position to act on physical objects can be subjected to scientific investigation. |
This means that if some people claim that they bend spoons “by the power of the spirit”, and given that they can do that repeatedly (hence what they do is verifiable), then it follows that they are free to visit the physicist’s lab and have the very physical phenomena that they cause examined under laboratory conditions.
In practice, of course, no one of those who claim the demolition — or even the insufficiency — of the known laws of physics ever goes to the lab, or allows the lab come near them, because they have much to lose from the exposure of their tricks. On the contrary, they profit greatly as long as their “powers” remain inscrutable and in the sphere of “mystery”.
Naturally, the phrase that was put in a frame, above, does not concern only the supposed “psychic powers”, but also anything assumed to be “supernatural”. Since the supernatural has some effect on the world of nature, it follows that the supernatural is a candidate for scientific investigation. People, for instance, who claim to hear voices, or see visions, or have contact with the dead, or with God, etc., do not actually claim things that are “beyond the limits of science”; after all, their brains, which receive such messages, are physical objects. Therefore, scientists should be given the chance to examine the brains of those people when they have such experiences, so that an attempt can be made to explain them. And, indeed, such attempts have been made and continue to be made, and the results so far are very interesting. (The interest lies in our understanding of how the brain manages to create illusions and deceive itself — these topics are examined in course Ν4.) So it is not true that there are some supposed “limits” beyond which science must not proceed. (Come to think of it, why science “must not” do so?) Such limits seem to be useful only to those who are afraid of the debunking of their beliefs.
The “Scientist’s Philosophy”, and Scientific “Beliefs”
Scientists have a “belief system”; i.e., they rely on a deep foundation of principles, which are practically never taught to them explicitly; but scientists learn those principles indirectly and develop their “beliefs” during their edification in science.
But here we should open a small parenthesis to point out that when we talk about “belief” (which we enclose in quotes) we don’t mean anything like the belief of a religious person, who never doubts what he or she believes; instead, we mean “belief” as in “hypothesis that is believed to be true with great — not, however, absolute — confidence.”
The “Belief” in the Objectivity of Nature
Deeply rooted in the scientist’s subconscious mind is the idea that the natural world exists “out there”, independently of the observer, and that it is objectively observable. That is, if two scientists observe the world, they must agree with the indications of their scientific instruments. The question of whether, for instance, a stone is hotter than another one, is not something decided by scientist X or Y, but by a thermometer. The thermometer, in this case, can be relied upon more than the opinion of anyone, no matter how intelligent that person is — that’s what “objectivity” means.
In general, due to the belief in the objectivity of nature, the scientist trusts the indications of instruments more than whatever has been written by others, whether scientists, philosophers, religious people, or thinkers of any kind. That is why in science we say: “Data take priority, theories follow.”
Let it be noted that in the second half of the 20th century a diverging opinion appeared, mainly among philosophers, but also among quantum physicists. Specifically, a flawed view prevailed according to which the observer influences the outcome of the experiment through observation, and, therefore, the human mind creates what we perceive as “reality”. Today, however, it has been understood that the “observer” is not necessarily a mind, and especially a conscious mind. An “observer” can also be a material particle, which can “create reality”, too. The view of 20th C. quantum physicists was based on a naïve and ill-defined notion of “consciousness”, a notion that was never described with precision by physicists — naturally, since it exceeds the limits of physics proper. So, one error was due to the fact that there is no scientific way by which we can define which observer is conscious and which one is not (therefore, which one creates — or does not create — reality); and a second error was that — as already mentioned — the ability to “observe” is one that belongs to matter in general, not to conscious observers only; so there is no issue of conscious observation, and therefore of a supposed subjective creation of reality. This issue is examined more thoroughly in course F3 (“Introduction to Quantum Physics”).
The “Belief” in the Understandability of Nature
Another “belief” of scientists is that the world is ultimately understandable. This means that every question that concerns the world of nature has a scientific answer. Perhaps we have not found that answer to this date, but by trying and investigating eventually we will find it. For example: we might not know today how a composer composes a new melody, or how a painter is inspired and creates a painting, so we say that art is, for the time being, out of the bounds of science. However, it is generally agreed upon among scientists that at some future time (perhaps after several decades), we will figure out the answers to all the questions that concern the natural world.
Let it be noted that the belief in the understandability of nature might be wrong. It might be (and perhaps it is so) that the human mind has some inherent limitations, which it cannot overcome by its nature. It could be that we live at times when those limitations have started becoming apparent. At present, however, most scientists are of the opinion that the world is ultimately understandable.
The “Belief” in the Economy of Nature
Another “belief”, similar to the above, is the following: the scientist believes that nature is, deep down, simple; and that if something appears complex to us, that is because our minds “confuse” us temporarily, because they cannot see things from a different perspective, from which things would appear simpler.
A typical example of that is the replacement of the geocentric model (which had the Earth at the center of the world) by the heliocentric model, which has the Earth orbiting the Sun. The geocentric model required that planetary orbits such as those of Mercury, Venus, Mars, etc., be extremely complex. Planets, as they appear from Earth (if we consider it immobile), seem to be moving in one direction, but at certain times they seem to be “applying the brakes”, coming to a standstill, and then turning around and moving in the opposite direction; then they decelerate again, stop, and turn once more to the original direction; and so on. In reality, this is an optical illusion, and it happens because the “internal” planets (Mercury and Venus, which are nearer the Sun than the Earth is) move faster than the Earth, which they reach and overtake; as soon as they reach the maximum distance from the Sun (from our vantage point of view) they appear as if they turn around and move in the opposite direction on the imaginary heavenly vault. Similarly, the Earth moves faster than the “external” planets (Mars, Jupiter, and Saturn — the rest were unknown in antiquity), which it overtakes, so we have the reverse phenomenon. Ancient Greeks (e.g., Aristotle, and later Ptolemy in Egypt), having the geocentric model in mind, concluded that the planets move along some complex curves that are called “epicycloids” in mathematics. Those are curves traced by the points of a circle that rolls on the periphery of another circle (see figure, below).
Example of an epicycloid curve
However, using the more appropriate heliocentric model, the orbits of the planets are simplified very much, turning into simple circles, as thinkers such as Aristarchus of Samos (and much later Copernicus) assumed initially; or into “near circles”, or ellipses, as Kepler concluded later, after he examined the astronomical data carefully.
Example of an ellipse
This kind of simplification of a physical theory happened once again, only a century ago, when Einstein proposed the theory of general relativity. According to this theory, although the planetary orbits appear to us as slowly rotating ellipses (see figure, below), in reality they are merely straight lines! But they are “straight” in a space of four dimensions: the space–time. In other words, the theory of relativity caused a simplification once again, but in order to understand this simplification we must abandon the way things are perceived by our minds in our everyday experience, and must move into a mathematical space of which we have no intuitive geometrical understanding.
Orbits of planets as rotating ellipses, simplified to “straight lines” by the theory of relativity
Similar simplifications appeared in physics when it became understood that electricity and magnetism are, in reality, two faces of the same coin: results of the electromagnetic force. In the past century another unification (read: simplification) occurred, when the weak and strong nuclear force were unified together with the electromagnetic force. Thus, now we have one theory that explains three out of the total four forces of nature, leaving out only the fourth of them, which is the force of gravity. In our times, scientists, due to their “faith” in the simplicity of nature, are trying to unify the force of gravity into the same model, so as to obtain a single theory that explains all four forces (the so-called “Theory of Everything”). Whether they succeed or not is a moot subject; but what we observe here is that their faith in the simplicity of nature guides them into trying to discover the simplest possible theory. A practical consequence is that great sums of money are spent in research in physics because of the existence of this faith, which leads the research into certain directions, avoiding others.
The faith in the simplicity of nature has been expressed already by the 14th century, by the English philosopher William of Ockham (often spelled as “Occam”), who stated what later became known as “Ockham’s Razor”:
|
Ockham’s Razor |
Examples related to religious opinions:
-
During the Medieval times, Christian theologians believed that the planets cruise along their orbits because there are angels who push them from behind. But when the theory of planetary motion became known (through Kepler’s laws and Newton’s theory of gravity, but also through its later update by Einstein), people understood that the angels are not needed, because even in their absence planets would still move in the ways we see them moving. Thus the angels were “excised” from the theory by Ockham’s Razor.
-
Even to this date, the average person believes that God created the stars (or that He keeps creating them, when people learn that stars keep being created all the time in our galaxy). But when it is understood how the interstellar dust collapses under the force of its own weight, and is accumulated in some spots where stars are created (in the course of several million years), then the action of God becomes redundant, because even if God does nothing, still stars will be created, just as the droplets of rain are created in a thick cloud and drop toward the earth, without God needing to do anything about it. Thus, Ockham’s Razor “excises” God, too, from the creation of stars. (Naturally, we mean specifically from the creation of stars; the reader should not interpret this to mean that Ockham’s Razor does away with God in general.)
Let’s see also a more abstract example. We saw, in a previous section, that having the numbers 2, 9, 14, 17, 18, 17, 14, 9, and 2, and placing them as dots along regular intervals according to their height, we can “summarize” them with a curve:

That curve is the “theory” that describes (and summarizes) the numbers, and seems to be sufficiently simple. But one might say that instead of the above curve we could summarize the data with the following one:
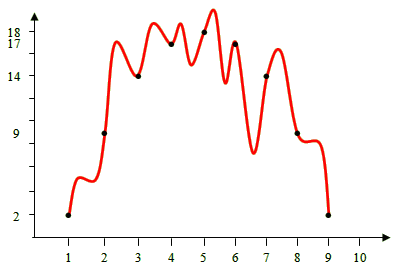
This curve, too, after all, passes through all the data, therefore it describes them correctly. It’s just that it looks a bit “crazy” in all the other points except those of the data. But why shouldn’t the above be the correct theory that describes all the given data?
If we have the opportunity to collect additional data, we can find out which of the two theories (the simple or the complex one) fits best to all the data (the old plus the additional ones). But if we don’t have that opportunity, or if we know that in order to obtain additional data we need to wait for technology of the future, then no one can preclude the possibility that the complex curve is the correct theory. We can, however, put aside the complex theory — temporarily — and prefer the simpler one, thanks to our belief in the simplicity of nature, using Ockham’s Razor. Also, what we discuss here is not merely a matter of a simple or a complex curve. (After all, how exactly is a “simple” or “complex” curve defined?) The reader probably remembers that the first (or “simple”) curve is described by the function: “y = 18 – (x – 5)2”. The second curve (the “complex” one) is also described by a function, but if we try to write down that function we’ll find out that it exceeds one line of this page in length. (For those who have the math background, it is a polynomial of the 16th degree.) Thus, the issue is not that the second curve appears complex simply to the eye, but every attempt to describe it is equally complex. This means that the second theory is inherently more complex than the first one. The reasoning behind its rejection is that, since Ockham’s Razor has worked wonders many times in the past, it is only natural to expect that it will work correctly again in the future — without however being absolutely sure that it must be so.
The belief in the simplicity of nature has deep historical roots. Ever since the antiquity, Greek thought expressed it very clearly. Ancient Greek thinkers attempted to explain the complexity that we see in nature by reducing it to some fundamental and simple substances: Thales thought that the base of everything was water; Heraclitus thought it to be fire; Pythagoras gave that title to numbers; Empedocles — and later Aristotle — thought that the fundamental elements were four: fire, air, earth, and water; Democritus thought that all is made of atoms; and so on. This deep belief of the Greeks in the simplicity of nature continued later in Western thought, but this time it acquired experimental justification: it was found that all is made (chemically) of 92 natural elements (the atoms); that the fundamental forces of nature are only four, and an attempt keeps being made to unify them all (see an earlier paragraph); that the subatomic particles that make up the atoms are only a few, etc. These issues are examined in more detail in course E2.
Exercise
Based on your overall understanding of what you learned from this course, try to answer the following question:
| Given that scientists have — like all humans — a subjective perception, is not the scientific edifice also necessarily subjective, and perhaps built out of the socially guided (hence, one-sided) perception of the scientists? |
Note: the above is also known as “Feyerabend’s thesis”.
Back to the home page of the I.C.S.