| Disc |
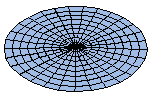 |
| 4 KB |
| Descendants of Disc | ||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
| Sphere |
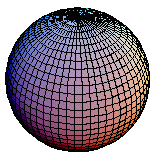 |
| 13 KB |
| Descendants of Sphere | ||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
In the summer of 2001, the author of this page read the book The Blind Watchmaker, by the British biologist Richard Dawkins.(1) Besides appreciating the wealth of information on the main subject of the book (evolution without design), an idea dawned on me: Dawkins' biomorphs (computer-generated 2-dimensional structures which "evolve" by being selected by a human-user of the program) could be implemented as 3-dimensional geometric surfaces, which I dubbed "geomorphs". The purpose of this variant of the project would not be to provide additional support to the theory of evolution (this is done in a wonderful way by Dawkins' book) but to allow the creation of visually interesting designs, just for the sake of inherent beauty they might present to the observer.
So I proceeded to implement the project, co-authoring it with a mathematician friend of mine, Maricarmen Martinez, who essentially did most of the program design (in Mathematica v. 4.0.1 -- see references at bottom -- which I had just started learning). My contribution, besides the initial idea, came mostly as a user of the program (download it from here), playing the role of the "environment", doing "natural selection" (selecting the "fittest" surfaces, according to my sense of esthetic merit). Maricarmen did a lot of environmental selection, too.
Our "genotype" (or, should I say, "geotype") is a set of parametric equations, employing a sum of products of trigonometric and polynomial functions. The genes of our geomorphs are coefficients of those formulas. By "mutating" the coefficients we get an evolutionary tree of surfaces having ancestral relationships to each other. If the reader wants to learn more details about the project, they may take a look at the text that follows the main table of this page (or simply click here).
Geomorphs that "survived" our selection procedure are available from the table below as GIFs, and the most interesting ones are animated. (Click on the images; notice the GIF size -- it may take a while to load the full image if you are using a slow modem connection.) The table depicts an evolutionary tree as follows: the left-most column shows the initial ancestors, a disc and a sphere, from which all the rest of the "species" descend. The second column shows descendants of the disc and sphere, the third column shows descendants of their descendants, and so on.
By the way, you may also visit our index of standard mathematical animated surfaces. Enjoy!
| Disc & Sphere | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Detailed Description of the "DNA" of our Geomorphs:
Each surface can be described by a general 3-D parametric formula of two free variables, as follows:
x = g1 (u, v)
y = g2 (u, v)
z = g3 (u, v)
where each g i (u, v) is a sum of (at most three, in our case, for simplification) products of functions Fj (Pol (u, v)), where j = 1,...,2 (thus every product has two factors, for simplification), and Pol(u,v) is a polynomial on u, v, of degree at most 2. Each function Fj is one of the following: either sine, or cosine, or the identity, or the constant zero function. Thus, if any of the Fj is zero, the whole term in the sum is nullified. On the other hand, if any of the Fj is the identity, it simply does not have any effect on the product. For the polynomials, we should mention that their general formula is:
Pol (u, v) = a0 + a1u + a2v + a3uv + a4u2 + a5v2
where each of the ak (k = 0,...,5) is a real number ranging in the interval [-3.0, 3.0]. All these specific values were decided to avoid adding even more parameters to the formulas above.
A surface (geomorph) is defined by deciding random values for the coefficients ak of the polynomials, choosing randomly the functions Fj from the list given above (sine, cosine, identity, zero), and deciding the range of the free variables u and v. However, the program generating geomorphs does not make completely arbitrary selections. Rather, it starts initially with a specific surface, which is either a flat disc, or a unit sphere. It then makes just one mutation, that is, it modifies one of the modifiable entities (i.e., either a coefficient value, or changing one of Fj) and repeats this one-mutation step (on the ancestor geomorph) a small number of times, resulting in a few new geomorphs, all simple descendants of the ancestor geomorph, which are proposed (shown graphically) for selection to the user. The user may either ignore the proposals and ask for more, or select one of the proposed geomorphs. In the latter case, the selected geomorph replaces the original one and the program proceeds generating variants of the mutated geomorph.
Through the program's interface the user may:
Thus, a whole "evolutionary tree" of ancestral relationships between geomorphs can be created, just as in Dawkins' original "biomorph" program.
Footnotes (clicking on the footnote-number, on the left, brings back to the text)
(1) Also, check this for a more detailed description of the Blind Watchmaker.
Click here to download a zip file
("geomorph.zip", 37 KB) which you can decompress
(unzip) in any new directory (folder) which you will create in
your system. You'll need to modify one directory path in the main
source notebook ("geomorph.nb") so that it matches the
newly created directory (mentioned above) where you'll decompress
the zip file. (You'll see comments to that effect in
"geomorph.nb".) Of course, you'll need Mathematica (see
below) to run the program. The program is provided free of
charge, free of viruses, and we are free of obligations.![]() Feel free to modify the
source in any way you find suitable, provided you append your own
authorship note to the already existent one (in other words,
don't delete the original note -- let the authorship
"evolve" along with its successive authors!
Feel free to modify the
source in any way you find suitable, provided you append your own
authorship note to the already existent one (in other words,
don't delete the original note -- let the authorship
"evolve" along with its successive authors!![]() ). No use of this program
is allowed for commercial purposes, resulting in direct or
indirect profit. (Although it would be remarkable if you could
somehow achieve this.
). No use of this program
is allowed for commercial purposes, resulting in direct or
indirect profit. (Although it would be remarkable if you could
somehow achieve this.![]() )
Enjoy the species you create!
)
Enjoy the species you create!
Dawkins, Richard (1986). The Blind Watchmaker: Why the evidence of evolution reveals a universe without design. W. W. Norton & Company: New York, 1986.
Mathematica v. 4.0.1.0 was used for writing the code of the program (Geomorph.nb) and, of course, for plotting the geomorphs.
A luxury yacht designer would probably realize that the boat geomorph is descended from a cone. A great deal of science and technology is used when designing the newest Sunseeker Yachts for sale today.