Πρόκειται να σας εξαφανίσωΉ αλλιώς: Γιατί ο χρόνος “ρέει” ενώ ο χώρος απλώς “είναι”? |
Πρόλογος (και μια προειδοποίηση)
Αγαπητέ επισκέπτη, επιτρέψτε-μου να συστηθώ. Είμαι ο περίφημος Μάγος Χάρρυ Φουντίνι και σκοπός του παρόντος κειμένου-μου είναι να σας εξαφανίσω. Ναι, πολύ σωστά διαβάσατε. Είναι πλήρως εντός των μαγικών-μου ικανοτήτων να σας κάνω να εξαφανιστείτε. Αλλά σας προειδοποιώ: μόλις εξαφανιστείτε, δεν θα μπορείτε ποτέ πια να επιστρέψετε· οπότε επαφίεται αποκλειστικά σ’ εσάς το αν θα συνεχίσετε να διαβάζετε περί αυτής της μαγικής πράξης. Υπάρχει και το κουμπί “Πίσω” του προγράμματος περιήγησής σας, οπότε αν ανήκετε στους λιγόψυχους σας συνιστώ ανεπιφύλακτα να το πατήσετε τώρα, διατηρώντας έτσι την ύπαρξή σας. Ότι είχα να πω το είπα. Εάν συνεχίσετε την ανάγνωση, μη με κατηγορήσετε για την επερχόμενη παύση της ύπαρξής σας.
Αφού λοιπόν έχω την συγκατάθεσή σας, θα προχωρήσω στη μαγική πράξη.
| Προκειμένου να σας εξαφανίσω, είναι απαραίτητο πρώτα να παγώσω τον κόσμο· δηλαδή να κάνω τον χρόνο να σταματήσει. Μόλις ο χρόνος σταματήσει, η εξαφάνισή σας θα κυλήσει αβίαστα, σαν το νερό στ’ αυλάκι. Προσδεθείτε λοιπόν στη θέση-σας, και συνεχίστε (αν τολμάτε) την ανάγνωση. |
Εντούτοις, δεν είναι δυνατό να φτάσουμε απευθείας στο κόλπο του παγώματος του χρόνου χωρίς κάποια προεργασία εκ μέρους σας. Θα πρέπει να περάσετε μια σειρά απλών νοητικών ασκήσεων. Αυτό είναι που θα σας βοηθήσω να κάνετε στη συνέχεια.
“Άνθρωποι σαν εμάς, που πιστεύουμε στη
φυσική, γνωρίζουμε οτι η διάκριση
μεταξύ παρελθόντος, παρόντος και μέλλοντος είναι μόνο
μια ψευδαίσθηση που επιμένει πεισματικά.”
Άλμπερτ Αϊνστάιν, Μάρτιος 1955
0. Εισαγωγή
Αρχικά θα εξοικειωθείτε με την ιδέα οτι η ανθρώπινη νόηση μας δίνει μια διαστρεβλωμένη, πολυπλοκότερη εικόνα του κόσμου από αυτήν που υπάρχει στην πραγματικότητα. Τα παραδείγματα που παρατίθενται σ’ αυτό το εισαγωγικό μέρος στοχεύουν στο να τονίσουν ακριβώς αυτή την παρατήρηση: η ανθρώπινη νόηση έχει την τάση να στρεβλώνει και να περιπλέκει την εικόνα της φύσης.
0.1 Τα φωτόνια μας δείχνουν ένα πράγμα, ο εγκέφαλός μας όμως βλέπει κάτι άλλο
Το πρώτο παράδειγμα είναι σχετικό με τη στρέβλωση της φωτεινότητας του φωτός: τα φωτόνια που φτάνουν στον αμφιβληστροειδή χιτώνα του ματιού-μας από δύο διαφορετικές περιοχές του εξωτερικού κόσμου έχουν την ίδια ένταση (φωτεινότητα), αλλά ο εγκέφαλός μας αρνείται να το αποδεχτεί, για τους δικούς-του λόγους. Παρατηρήστε την παρακάτω εικόνα.

Εικόνα 0.1. Η αυταπάτη της σκακιέρας: οι περιοχές A και B στη σκακιέρα έχουν την ίδια απόχρωση του γκρι (εκ του Edward H. Adelson)
Ρίξτε μια ματιά στα τετράγωνα με τη σήμανση Α και Β, πάνω στην σκακιέρα. Παρόλο που τα μάτια-σας σας λένε οτι το τετράγωνο Α είναι “μαύρο” και το τετράγωνο Β “άσπρο”, στην πραγματικότητα οι αποχρώσεις του γκρι που χρησιμοποιήθηκαν για να χρωματιστούν αυτά τα δύο τετράγωνα (όχι τα γράμματα Α και Β, αλλά το φόντο των τετραγώνων) είναι πανομοιότυπες! Αρνείστε να το πιστέψετε; Δεν είστε οι μόνοι: σχεδόν όλοι όσοι αντιμετωπίζουν αυτή την αυταπάτη για πρώτη φορά παραμένουν δύσπιστοι. Η αντίδραση ενός φίλου-μου, όταν πρωτοαντίκρισε την εικόνα αυτή, ήταν να την αποθηκεύσει τοπικά στον δίσκο-του, έπειτα να την ανοίξει με το πρόγραμμα ζωγραφικής του λειτουργικού-του συστήματος, και να επιλέξει ένα μικρό κομμάτι από το τετράγωνο Α (ένα μικρό ορθογώνιο παραλληλόγραμμο σε μία περιοχή κοντά στο γράμμα Α), και μετά να το σύρει μετακινώντας-το στο τετράγωνο Β. Παρατήρησε τότε οτι το μικρό ορθογώνιο “εξαφανιζόταν” καθώς το μετακινούσε εντός των ορίων του τετραγώνου Β (επειδή αναμιγνυόταν τέλεια με το χρώμα αυτού του τετραγώνου· φυσικά, αφού είναι το ίδιο χρώμα!). Για δική-σας ευκολία, το έκανα αυτό ήδη στην παραπάνω εικόνα: μπορείτε να δείτε τα δύο γράμματα Α και Β αντιγραμμένα στην κάτω–δεξιά γωνία της εικόνας, μαζί με το φόντο-τους. Εκεί βλέπετε οτι — εκτός “συμφραζομένων” — οι δύο αποχρώσεις φαίνονται πανομοιότυπες. Ένας άλλος τρόπος για να το δείτε, εάν συνεχίζετε να μη με πιστεύετε, είναι να πάρετε ένα φύλλο χαρτί (χρειάζεται να είναι σχετικά αδιαφανές όμως) και να ανοίξετε δύο μικρές τρύπες τη μία πάνω από την άλλη, περίπου στην απόσταση των τετραγώνων Α και Β. Έπειτα, αν καλύψετε την εικόνα με το φύλλο, θα διαπιστώσετε οτι το χρώμα που διέρχεται από τις δύο τρύπες είναι, ως δια μαγείας, η ίδια απόχρωση του γκρι. Σας προτείνω να δοκιμάσετε οποιαδήποτε από αυτές τις δύο μεθόδους, σε περίπτωση που δεν είστε ήδη εξοικειωμένοι με αυτή την εκπληκτική αυταπάτη.
Ωραία, αλλά τί συμβαίνει εν προκειμένω; Το φως που φτάνει στους αμφιβληστροειδείς-σας από τα τετράγωνα Α και Β έχει ακριβώς την ίδια ένταση. Αυτό σημαίνει οτι ο ίδιος αριθμός φωτονίων φτάνει στα μάτια-σας ανά μονάδα χρόνου. Τα ραβδία και τα κωνία (κυρίως τα κωνία) που λαμβάνουν αυτά τα φωτόνια σε δύο αντίστοιχα μικροσκοπικά σημεία των αμφιβληστροειδών-σας, ερεθίζονται με σχεδόν πανομοιότυπο τρόπο· οπότε και στέλνουν το ίδιο σήμα στον οπτικό φλοιό, στο οπίσθιο τμήμα του εγκεφάλου, τόσο για το τετράγωνο Α όσο και για το τετράγωνο Β. Αλλά το τί κάνει ο οπτικός φλοιός με αυτά τα πανομοιότυπα σήματα είναι μια άλλη ιστορία. Το οπτικό σύστημα θέλει να δει ένα καρό μοτίβο από τετράγωνα σε ένα μέρος του οποίου ένα αντικείμενο προβάλλει τη σκιά του. Έτσι ο εγκέφαλος διορθώνει αυτόματα τις εντάσεις του φωτός και νοερά “αφαιρεί” τη σκιά του αντικειμένου, αφήνοντας τα τετράγωνα όπως “θα έπρεπε” να είναι, δηλαδή άσπρο και μαύρο, ώστε να μας πληροφορήσει πως υπάρχει ένα μοτίβο σκακιέρας εκεί το οποίο επισκιάζεται κατά τρόπο διαγώνιο. Τώρα, παρατηρείστε οτι η λειτουργία του εγκεφάλου δικαιολογείται θαυμάσια. Φανταστείτε ποιο θα ήταν το αποτέλεσμα αν ο εγκέφαλος δεν μπορούσε να το κάνει αυτό: αντί για ένα καρό μοτίβο με σκιά θα βλέπαμε την εικόνα όπως είναι “κατά κυριολεξία”· δηλαδή θα βλέπαμε μία περιοχή σχήματος ρόμβου με διάσπαρτες περιοχές ποικίλων γκρι μπαλωμάτων, άλλες φωτεινότερες, άλλες πιο σκούρες με διαγώνιες ζώνες κοντά στο κέντρο (όπου σε υψηλότερο επίπεδο αντιλαμβανόμαστε τη σκιά), συν μερικές κατακόρυφες ζώνες με αποχρώσεις του πράσινου, λίγες από τις οποίες σχηματίζουν μια ελλειπτική περιοχή στην πάνω δεξιά γωνία. Αυτό που μόλις περιέγραψα είναι μια “περιγραφή κατώτερου επιπέδου” της εικόνας, την οποία μπορεί επίσης να κάνει οποιοδήποτε απλοϊκό πρόγραμμα επεξεργασίας εικόνας σε υπολογιστή. Όμως αυτό που κάνει ο εγκέφαλος δεν είναι καθόλου απλοϊκό, αλλά πολυσύνθετη επεξεργασία εικόνας που μας επιτρέπει να δούμε αμετάβλητα μοτίβα στο κόσμο (π.χ. μια σκακιέρα), ανεξάρτητα από το πώς σκιάζονται, επικαλύπτονται, στρέφονται, φωτίζονται, υπερφωτίζονται, μεγεθύνονται, σμικρύνονται, ή μεταβάλλονται υπό την επίδραση διάφορων άλλων οπτικών μετασχηματισμών. Είναι ζωτικής σημασίας το οτι οι εγκέφαλοι μπορούν και το κάνουν αυτό. Ή τουλάχιστον, ήταν απαραίτητο — ζήτημα ζωής και θανάτου — σε ένα στάδιο της εξελικτικής-μας ιστορίας, όταν οι πρόγονοί μας έπρεπε να διακρίνουν το θήραμα και τα αρπακτικά κάτω από μια ποικιλία συνθηκών φωτισμού. Όσοι από τους προγόνους-μας είχαν αυτή την ικανότητα, έζησαν για να αναπαραχθούν και να τη μεταδώσουν στους νεότερους· ενώ όσοι τη στερούνταν ή είχαν μειωμένες ικανότητες, ήσαν επιρρεπείς στο να μην επιβιώσουν καθώς γίνονταν θηράματα ή αντιμετώπιζαν άλλες δυσκολίες.
Όμως, αφήνοντας τις εξελικτικές εξηγήσεις κατά μέρος, η ουσία του θέματος είναι οτι στην περίπτωση της αυταπάτης της σκακιέρας, τα φωτόνια μας δίνουν έναν τύπο σήματος, αλλά ο εγκέφαλός μας τον ερμηνεύει διαφορετικά, ανάλογα με τα “συμφραζόμενα” (το φόντο). Αυτή είναι μια περίπτωση νοητικής “στρέβλωσης”, όπου ο ανθρώπινος εγκέφαλος καταγράφει κάτι διαφορετικό από αυτό που θα κατέγραφαν τα εργαστηριακά όργανα (π.χ. τα φωτοκύτταρα μιας κάμερας). Όπως θα υποπτεύεστε, η αυταπάτη της σκακιέρας δεν είναι ένα ιδιόμορφο και απομονωμένο παράδειγμα, αλλά μάλλον αρκετά τυπικό, μέρος του νοητικού οπλοστασίου του εγκεφάλου. (Παρεμπιπτόντως, εάν σας άρεσε αυτή η αυταπάτη, μπορείτε κάποια στιγμή να επισκεφθείτε αυτή τη σελίδα — στα αγγλικά — που περιλαμβάνει πολλά άλλα παραδείγματα.) Τώρα ας προχωρήσουμε σε ένα παράδειγμα όπου ο εγκέφαλος “περιπλέκει” τον κόσμο (πάλι για τους δικούς-του, βιολογικά σημαντικούς λόγους).
0.2 Δεν υπάρχουν χρώματα στον κόσμο· το μυαλό-μας τα πλάθει!
Όταν ήμουν μικρός συνήθιζα να θαυμάζω την αρμονία και ομορφιά των χρωμάτων του ουράνιου τόξου. Είχα “κλέψει” ένα κρύσταλλο σε σχήμα πρίσματος από τον πολυέλαιο που διακοσμούσε το ταβάνι της τραπεζαρίας του σπιτιού των γονιών-μου (με φόβο πάντα οτι η μαμά ή ο μπαμπάς θα παρατηρούσαν το κομμάτι που έλειπε, αλλά παραδόξως ποτέ κανένας-τους δεν το παρατήρησε), και άφηνα το ηλιακό φως να περνά μέσα από αυτό, παράγοντας ένα όμορφο φωτεινό μοτίβο ουράνιου τόξου στον τοίχο του δωματίου-μου. Αναρωτιόμουν, κοιτώντας το ουράνιο τόξο, αν υπάρχουν περισσότερα χρώματα από αυτά που τα μάτια-μας είναι ικανά να δουν.
![]()
Εικόνα 0.2. Το ορατό τμήμα του ηλεκτρομαγνητικού φάσματος
Ελάχιστα γνώριζα τότε. Όπως έμαθα αργότερα, πράγματι υπάρχουν περισσότερα “χρώματα” — πολύ περισσότερα μάλιστα από αυτά που μπορούμε να δούμε — εκτεινόμενα σε μια εξαιρετικά ευρεία έκταση. Αυτή η έκταση λέγεται ηλεκτρομαγνητικό φάσμα.
Το φως αποτελείται από φωτόνια, και ένας τρόπος για να φανταστούμε τα φωτόνια είναι σαν κύματα που ταξιδεύουν στο διάστημα. Κάθε κύμα έχει ένα χαρακτηριστικό μήκος κύματος, το οποίο είναι το μήκος μεταξύ δύο διαδοχικών κορυφών (ή αυλακιών — δείτε την εικόνα παρακάτω). Αυτό το μήκος κύματος των φωτονίων — ένας απλός αριθμός — είναι αυτό που αντιλαμβανόμαστε ως “χρώμα”. Το κόκκινο, π.χ., συνίσταται από φωτόνια με συγκεκριμένο μήκος κύματος (γύρω στα 650 nm, ή 650 δισεκατομμυριοστά του μέτρου). Το κίτρινο είναι φωτόνια με μικρότερο μήκος κύματος (γύρω στα 570 nm)· το πράσινο ακόμα πιο μικρό (γύρω στα 510 nm)· και ούτω καθεξής, έως το σκοτεινό ιώδες, που είναι φωτόνια με το μικρότερο μήκος κύματος που μπορούν να δουν τα μάτια-μας (γύρω στα 400 nm). Η ακόλουθη εικόνα συγκρίνει τα μήκη κύματος τριών χρωμάτων, μεγεθύνοντας υπέρμετρα τα μήκη, αλλά διατηρώντας τα σχετικά μεγέθη υπό κλίμακα.
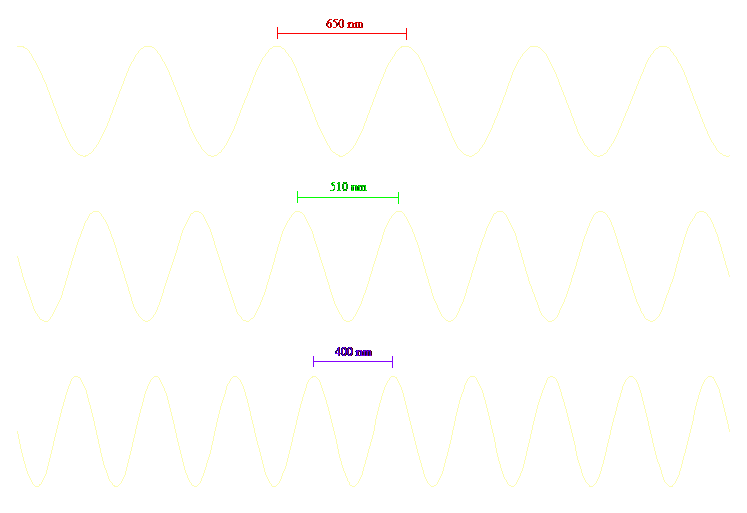
Εικόνα 0.3. Μήκος κύματος τριών χρωμάτων: κόκκινο, πράσινο και ιώδες (σχεδιασμένα υπό κλίμακα)
Αλλά το μήκος κύματος δεν τελειώνει στο ιώδες απλά και μόνο επειδή τα μάτια-μας δεν μπορούν να δουν φωτόνια με μικρότερο μήκος κύματος. Πέρα από το ιώδες, μέχρι περίπου τα 10 nm, υπάρχει το υπεριώδες, ένα “χρώμα” που είναι αόρατο μεν σ’ εμάς, ορατό δε σε μερικά έντομα, όπως οι μέλισσες και οι σφήκες. (Επίσης, μερικά αγριολούλουδα που εμφανίζονται άσπρα στο ανθρώπινο μάτι, στην πραγματικότητα αντανακλούν το υπεριώδες χρώμα· κ’ έτσι, έντομα και φυτά έχουν αλληλο-προσαρμοστεί: τα μεν έντομα να είναι ικανά ν’ αντιληφθούν αυτό το χρώμα, τα δε φυτά να το αντανακλούν, ώστε να προσελκύουν τα έντομα.) Όσο πιο μικρό είναι το μήκος κύματος, τόσο περισσότερη ενέργεια μεταφέρουν τα φωτόνια αυτού του “χρώματος”. Έτσι, το υπεριώδες μεταφέρει περισσότερη ενέργεια από όλα τα άλλα χρώματα του ορατού φάσματος, και είναι υπεύθυνο για το μαύρισμα του δέρματός μας που εκτίθεται στο φως του ήλιου. Η υπερβολική έκθεση σε υπεριώδη φωτόνια μπορεί να κάψει το δέρμα μας, ευτυχώς όμως (και αυτό είναι σημαντικό σε ότι ακολουθεί) η στοιβάδα του όζοντος της ατμόσφαιρας του πλανήτη-μας αντανακλά τα περισσότερα υψηλής ενέργειας φωτόνια που οργώνουν το διάστημα (που τα περισσότερα έχουν παραχθεί από τον Ήλιο). Παρόμοια, φωτόνια στο εύρος των ακτίνων Χ (μεταξύ 10 nm και 0,01 nm) έχουν μικρότερο μήκος κύματος απ’ ότι τα υπεριώδη, και μεταφέρουν αρκετή ενέργεια ώστε να διαπερνούν μαλακούς ιστούς, καθιστώντας τις ακτίνες Χ χρήσιμες στην ιατρική· αλλά, όπως όλοι γνωρίζουν, η υπερβολική έκθεση στις ακτίνες-Χ καταστρέφει τους ιστούς (πολύ πιο γρήγορα από την υπεριώδη ακτινοβολία) και είναι θανατηφόρα σε μεγάλες ποσότητες καθώς προκαλεί καρκίνο. Οι ακτίνες γάμμα έχουν ακόμα μικρότερο μήκος κύματος (μεταξύ 0,01 nm και 0,000001 nm, ή και μικρότερο), είναι θανατηφόρες, και τα περισσότερα στερεά αντικείμενα είναι σχεδόν εξολοκλήρου διαφανή σε αυτές (όχι όμως και η οζονόσφαιρα, παρόλα αυτά). Μερικά εγχειρίδια περιλαμβάνουν και την κοσμική ακτινοβολία στο φάσμα, παρόλο που αυτή δεν αποτελείται από φωτόνια αλλά από σωματίδια εξαιρετικά μεγάλης ενέργειας που έρχονται από το απώτερο διάστημα, και έχουν μήκος κύματος που μπορεί να είναι ακόμα μικρότερο από εκείνο των ακτίνων γάμμα.

Εικόνα 0.4. Ολόκληρο το ηλεκτρομαγνητικό φάσμα (όχι υπό κλίμακα)
Επίσης, ούτε με το κόκκινο αρχίζουν τα μήκη κύματος, όπως δείχνει η εικόνα 0.4. Τα μήκη κύματος που είναι μεγαλύτερα (μέχρι 1 mm, δηλαδή 1 χιλιοστόμετρο) από το κόκκινο (ερυθρό) ανήκουν στο “χρώμα” υπέρυθρο, που παράγεται όταν σβήνουμε το λαμπερό και κόκκινο από τη ζέστη θερμαντικό σώμα (ή το μάτι της κουζίνας που έχει πυρώσει), μόλις η ερυθρότητα του σιδήρου εξαφανιστεί αλλά ενώ είναι ακόμα ζεστό. Οποιοδήποτε θερμό αντικείμενο στην πραγματικότητα λάμπει στο υπέρυθρο, συμπεριλαμβανομένων και των σωμάτων-μας. Νά γιατί τα κουνούπια μπορούν να μας εντοπίσουν στο σκοτάδι: μπορούν να δουν στο υπέρυθρο, οπότε γι’ αυτά είμαστε θερμά λαμπερά αντικείμενα (η καλύτερα, σερβιρισμένα ζεστά γεύματα). Πέρα από το υπέρυθρο (με μήκη κύματος μέχρι και 10 cm) υπάρχουν τα μικροκύματα (τα οποία κάνουν τους φούρνους μικροκυμάτων-μας να λειτουργούν), και τα ραδιοκύματα (που κάνουν τα ραδιόφωνα, τις τηλεοράσεις και τα κινητά-μας τηλέφωνα να λειτουργούν). Εάν επιθυμείτε περισσότερες πληροφορίες πάνω στο ηλεκτρομαγνητικό φάσμα, και ειδικότερα για να δείτε το ορατό φάσμα σχεδιασμένο σε (λογαριθμική) κλίμακα εντός αυτού, μπορείτε να επισκεφτείτε αυτή τη σελίδα της αγγλικής Wikipedia. Σημειώστε οτι η εικόνα 0.4, παραπάνω, υπερβάλλει κατά πολύ στο εύρος του ορατού τμήματος εντός του όλου ηλεκτρομαγνητικού φάσματος· εάν το ορατό φάσμα έπρεπε να δειχτεί υπό κλίμακα, θα εξαφανιζόταν εντελώς, απαιτώντας πλάτος μικρότερο του ενός pixel για να σχεδιαστεί στην οθόνη του υπολογιστή-μας!
Η προηγούμενη εξέταση του ηλεκτρομαγνητικού φάσματος μας δείχνει δύο βασικά πράγματα: πρώτο, παρόλο που τα μήκη κύματος των φωτονίων ποικίλουν σε τεράστιο εύρος, το οπτικό-μας σύστημα έχει προσαρμοστεί στο να αντιλαμβάνεται μόνο ένα ελάχιστο τμήμα αυτού του εύρους· και δεύτερο, ακόμα και μέσα σ’ αυτό το τμήμα του φάσματος που βλἐπουμε, παρόλο που τα μήκη κύματος αλλάζουν κατά συνεχή τρόπο, το οπτικό-μας σύστημα έχει “διακριτοποιήσει” αυτή τη συνεχή έκταση: την έχει χωρίσει κατά αυθαίρετο τρόπο σε ανύπαρκτες περιοχές, δηλαδή σ’ αυτά που ονομάζουμε “χρώματα”.
Η τελευταία αυτή ιδέα είναι πολύ απλή: στον κόσμο δεν υπάρχουν χρώματα, όπως κόκκινο, πράσινο, μπλε κλπ. Υπάρχουν μόνο αριθμοί που ποικίλουν κατά συνεχή τρόπο, όπως 400, 401, 402, κ.ο.κ. (Ακόμα και μεταξύ των 400 και 401 υπάρχουν οι αριθμοί 400,5, 400,25, κ.ο.κ). Αλλά αντί να αντιλαμβανόμαστε ένα συνεχές εύρος αριθμών για μήκη κύματος (παρόμοια, ας πούμε, με τον τρόπο που αντιλαμβανόμαστε ένα συνεχές εύρος θερμοκρασιών), αντιλαμβανόμαστε ολόκληρες περιοχές του φάσματος που ονομάζουμε κόκκινο, κίτρινο, πράσινο, κ.ο.κ. Το οτι δίνουμε ονόματα στα χρώματα αποδεικνύει οτι εμείς κάνουμε αυτή την αντιληπτική “διακριτοποίηση” (το χώρισμα σε κομμάτια). Για παράδειγμα, υπάρχει μια περιοχή εντός αυτού που ονομάζουμε “πράσινο χρώμα”, (στα μήκη κύματος μεταξύ περίπου 490 και 530 nm), στην οποία είναι αδύνατο για το οπτικό μας σύστημα να δει παραπάνω από μια απόχρωση του πράσινου, έτσι ώστε ονομάζουμε ολόκληρη αυτή την περιοχή “πράσινο”. (Σημειώστε οτι οι επιστήμονες έχουν χωρίσει ακόμα και το αόρατο τμήμα του φάσματος σε διακριτά κομμάτια, όπως το “υπεριώδες”, “υπέρυθρο” κλπ., αλλά για πρακτικούς λόγους, άσχετους με την ανθρώπινη αντίληψη.) Γιατί οι εγκέφαλοί μας το κάνουν αυτό; Γιατί μας δείχνουν μόνο ένα μικροσκοπικό τμήμα μιας πολύ μεγαλύτερης πραγματικότητας; Και γιατί χωρίζουν αυτό το μικροσκοπικό τμήμα της πραγματικότητας σε περιοχές, δηλαδή τα χρώματα, τα οποία δεν υπάρχουν εκτός της ανθρώπινης και ζωικής όρασης;
Υπάρχει και πάλι ένας εξελικτικός λόγος που εξηγεί γιατί αντιλαμβανόμαστε μόνο ένα μικροσκοπικό τμήμα ολόκληρου του φάσματος: αυτό συμβαίνει επειδή το μεγαλύτερο μέρος της ηλεκτρομαγνητικής ακτινοβολίας που εκπέμπεται από τον Ήλιο και φτάνει στην επιφάνεια του πλανήτη-μας τυχαίνει να ανήκει σχεδόν ακριβώς στο ορατό φάσμα. Κατά συνέπεια, τα ζώα προσαρμόστηκαν στο να αντιλαμβάνονται φωτόνια στην περιοχή του φάσματος που είναι διαθέσιμη, παρόλο που μερικά από αυτά, όπως είδαμε (μέλισσες, κουνούπια), κατάφεραν να διερευνήσουν τις παρυφές αυτού του φάσματος, όπου τα φωτόνια είναι λιγότερο άφθονα. Το υπόλοιπο του φάσματος είναι είτε μη διαθέσιμο λόγω της ζώνης του όζοντος στην ατμόσφαιρά μας είτε δεν παράγεται από τον Ήλιο σε τόσο άφθονες ποσότητες όσο η ακτινοβολία στο ορατό τμήμα του φάσματος. Δεν είναι λοιπόν καθόλου περίεργο το οτι εμείς, τα ζωικά είδη της Γης, βλέπουμε μόνο αυτό το μικροσκοπικό τμήμα του φάσματος: εξελιχθήκαμε ν’ αντιλαμβανόμαστε αυτό που μας είναι διαθέσιμο· δεν θα μπορούσαμε ποτέ να εξελιχθούμε για να βλέπουμε αυτό που δεν είναι διαθέσιμο εδώ, σ’ αυτή τη γωνιά του κόσμου όπου υπάρχουμε.
Υπάρχει επίσης ένας φυσιο-λογικός (της φυσιολογίας) λόγος που εξηγεί γιατί διακριτοποιούμε το συνεχές ορατό φάσμα σε περιοχές, τα χρώματα. Αυτό συμβαίνει επειδή τα κωνία (τα φωτοϋποδεκτικά κύτταρα των αμφιβληστροειδών-μας) διακρίνονται σε τρεις τύπους, σύμφωνα με τη χρωστική ουσία που περιέχουν: αυτά με τη χρωστική που δέχεται κυρίως φωτόνια στην έκταση του μπλε, και έπειτα άλλα με χρωστικές για την έκταση του πράσινου και του κόκκινου. Η ενδιάμεση ενεργοποίηση αυτών των υποδοχέων μας κάνει να αντιλαμβανόμαστε τα μεταξύ-τους χρώματα, όπως το πορτοκαλί, το κίτρινο, το κυανό, το πορφυρό, κλπ. (Παραλλαγές σε δύο άλλες παραμέτρους, τη φωτεινότητα του χρώματος και τον κορεσμό-του, οδηγούν σε χρώματα που αντιλαμβανόμαστε σαν ροζ, καφέ, λαδί, άσπρο, μαύρο, και όλα τα υπόλοιπα.)
Με άλλα λόγια, το συμπέρασμα αυτής της υποενότητας είναι οτι ο φυσικός κόσμος υπάρχει με κάποιον ιδιαίτερο, αντικειμενικό τρόπο (στην περίπτωση του φωτός πρόκειται για μια αχανή συνεχόμενη έκταση αριθμών), αλλά η νόησή μας μας αναγκάζει να τον αντιλαμβανόμαστε με ένα τελείως διαφορετικό, υποκειμενικό τρόπο (ένα πολύ στενότερο φάσμα από διακριτές περιοχές, τα “χρώματα”). Έτσι, χρειαζόμαστε τα εργαστηριακά-μας όργανα — και τη γνώση των σχετικών τομέων της φυσικής — ώστε να συνειδητοποιήσουμε την “νοητική εξαπάτηση” που υφιστάμεθα καθημερινά.
Ας συνεχίσουμε βλέποντας πώς η νόησή μας μας “εξαπατά”, με ένα παράδειγμα μιας κάπως πιο αφηρημένης φύσης.
0.3 Ο εγκέφαλος λυγίζει “ευθείες γραμμές”, μετατρέποντάς τες σε κύκλους!
Πρώτα, πριν πάμε σε ότι υποδηλώνει ο τίτλος του παρόντος εδαφίου, ορίστε ένα απλό παράδειγμα που δείχνει οτι η ανθρώπινη νόηση τείνει να δει κάτι σύνθετο, όταν η πραγματικότητα είναι απλούστερη: σκεφτείτε τον τρόπο με τον οποίο οι αρχαίοι λαοί πίστευαν οτι κινούνται οι πλανήτες στον ουράνιο θόλο. Πιστεύοντας οτι η Γη είναι σταθερή, και στο κέντρο του σύμπαντος, θεωρούσαν οτι οι πλανήτες έχουν σύνθετες τροχιές στην ουράνια σφαίρα κατά τη διάρκεια των μηνών ή ετών, άλλοτε κινούμενοι σε μια κατεύθυνση, άλλοτε επιβραδυνόμενοι, σταματώντας, και γυρνώντας για να κινηθούν ανάποδα. Το νόμιζαν αυτό επειδή στην πραγματικότητα η Γη περιφέρεται γύρω από τον Ήλιο γρηγορότερα από τους εξωτερικούς πλανήτες (Άρης, Δίας, κλπ.), ώστε σε κάποιο χρονικό σημείο τους προσπερνά, κάνοντάς τους να φαίνονται σαν να κινούνται προς τα πίσω. Επίσης, οι εσωτερικοί πλανήτες Ερμής και Αφροδίτη κινούνται γρηγορότερα απ’ ότι η Γη, την οποία και προσπερνούν μέσα σε ένα μόνο έτος. Οι αρχαίοι Έλληνες ανακάλυψαν μάλιστα ένα μαθηματικό μοντέλο για να περιγράψουν όλη αυτή την πολυπλοκότητα: ήταν η θεωρία των “επικύκλων” του Πτολεμαίου (2ος αι. μ.Χ.), η οποία θεωρούσε τη Γη ακίνητη στο κέντρο του σύμπαντος, και τους πλανήτες να περιφέρονται γύρω-της, διαγράφοντας αυτό που θεωρείτο “κύκλοι μέσα σε κύκλους”, ή “επίκυκλοι”. Όμως δεν σκέφτονταν όλοι οι αρχαίοι διανοητές έτσι. Ο Έλληνας αστρονόμος Αρίσταρχος ο Σάμιος (γύρω στο 270 π.Χ.) πρότεινε οτι ο Ήλιος βρίσκεται στο κέντρο, και η Γη με τους άλλους πλανήτες περιφέρονται γύρω από τον Ήλιο· το οποίο είναι μεν σωστό, αλλά σαν ιδέα ήταν πολύ μπροστά από την εποχή-της για να εξεταστεί σοβαρά. Τo γεωκεντρικό μοντέλο του Πτολεμαίου έμοιαζε πιο λογικό, καθώς περιέγραφε αυτό που οι άνθρωποι έβλεπαν με το μάτι. Το γεωκεντρικό μοντέλο απλουστεύτηκε σημαντικά όταν ο Πολωνός ιερέας και αστρονόμος Mikolaj Kopernik (γνωστός ως Κοπέρνικος, 1473–1543) ανακάλυψε εκ νέου το “ηλιοκεντρικό” μοντέλο του Αρίσταρχου, μετατρέποντας όλες τις τροχιές των πλανητών σε απλούς κύκλους. Οι κύκλοι έγιναν λίγο πιο πολύπλοκοι αργότερα από τον Γερμανό αστρονόμο Johannes Kepler (1571 – 1630), που διαπίστωσε οτι δεν είναι κύκλοι αλλά ελλείψεις· και ακόμα μια φορά αργότερα από τον Albert Einstein (1879 – 1955), του οποίου η θεωρία της γενικής σχετικότητας έδειξε οτι οι ελλείψεις στη πραγματικότητα περιστρέφονται αργά. Αλλά ακόμα και έτσι, αυτά όλα αποτελούσαν μεγάλη απλούστευση συγκρινόμενα με το Πτολεμαϊκό γεωκεντρικό σύστημα. Άλλωστε η “πολυπλοκοποίηση” του Αϊνστάιν είναι μόνο φαινομενική· στην πραγματικότητα είναι κι αυτή μια απλούστευση, και σύντομα θα δούμε γιατί.
Μια παρόμοια απλούστευση συνέβη κατά το 17ο αιώνα, σύντομα μετά την αποκατάσταση του ηλιοκεντρικού συστήματος από τον Κοπέρνικο, όταν ο Sir Isaac Newton (Νεύτων) συνειδητοποίησε οτι η καθοδική κίνηση οποιουδήποτε αντικειμένου που έλκεται από τη βαρύτητα της Γης και η κυκλική κίνηση της Σελήνης γύρω από τη Γη, είναι στην πραγματικότητα όψεις του ίδιου φαινομένου. Τόσο ένα μήλο που ωρίμασε και πέφτει από το δέντρο, όσο και το Φεγγάρι, πέφτουν προς τη Γη. Πρέπει να σημειωθεί οτι ο νόμος του Νεύτωνα που περιγράφει την ομοιότητα των δύο κινήσεων εφαρμόζεται αμφίδρομα, ούτως ώστε η Σελήνη έλκει επίσης τη Γη, διαταράσσοντας την τροχιά της τελευταίας κατά έναν πολύ μικρό βαθμό· αλλά και το μήλο κάνει το ίδιο πράγμα, μόνο που ο βαθμός της διαταραχής της τροχιάς της Γης από το μήλο είναι εντελώς αμελητέος.

Εικόνα 0.5. Απλούστευση (γενίκευση) δύο τύπων κίνησης που αρχικά θεωρούνταν διακριτοί
(Η παραπάνω εικόνα υπαινίσσεται και επαναλαμβάνει το μύθο οτι ο Νεύτωνας συνέλαβε την απλούστευσή του — ή γενίκευση — όταν κάθισε κάτω από μια μηλιά και δέχτηκε ένα μήλο στο κεφάλι-του. Ασχέτως από το πόσο μακριά από την αλήθεια είναι αυτός ο μύθος, βρίσκω οτι έχει μια κάποια εκπαιδευτική αξία: καθιστά εύκολο στους μαθητές να μάθουν και να θυμούνται μια βαθιά ιδέα, οπότε δεν αισθάνομαι κανέναν ενδοιασμό να τον επαναλάβω εδώ.)
Αυτό που θέλω να συζητήσω, ωστόσο, παρόλο που αφορά πλανητικές τροχιές, δεν αφορά σε ιδέες που μαθαίνει κάθε σχολιαρόπαιδο, όπως την εύκολη απλούστευση από το γεωκεντρικό στο ηλιοκεντρικό μοντέλο, ή τη γενίκευση μεταξύ της κίνησης μήλων που πέφτουν και δορυφόρων σε τροχιά. Πρόκειται για μια απλούστευση που οι περισσότεροι άνθρωποι δεν συναντούν, εκτός και αν μελετήσουν μαθηματικά, φυσική, και/ή αστρονομία. Αυτή η απλούστευση, που έγινε δυνατή μόνο μετά τη γενική σχετικότητα του Αϊνστάιν, λέει οτι οι τροχιές των ουράνιων σωμάτων στην πραγματικότητα δεν είναι κύκλοι, ελλείψεις, παραβολές ή άλλες εξωτικές καμπύλες (“κωνικές τομές” καθώς ονομάζονται), αλλά... ευθείες γραμμές!
Πιστεύετε οτι ξέρετε τί είναι ευθεία γραμμή; Στο σχολείο μαθαίνουμε οτι ευθεία γραμμή είναι η συντομότερη διαδρομή μεταξύ δύο σημείων. Αυτό είναι μια χαρά ως ορισμός, και συμπίπτει με την διαισθητική αντίληψή μας της ευθείας γραμμής όταν ο χώρος είναι επίπεδος, όπως ένα επίπεδο φύλλο χαρτιού δύο διαστάσεων. Ωστόσο, όταν ο χώρος είναι κυρτός, όπως η επιφάνεια μιας σφαίρας, τότε το συντομότερο μονοπάτι που συνδέει δύο σημεία δεν είναι η ευθεία γραμμή, επειδή δεν υπάρχουν ευθείες στην επιφάνεια μιας σφαίρας. Βέβαια, η ιδέα που έρχεται στο μυαλό ενός μη-μαθηματιικού καθώς διαβάζει τα προηγούμενα είναι οτι εξακολουθεί να υπάρχει μια ευθεία γραμμή που συνδέει τα σημεία της σφαίρας: είναι μια ευθεία που ξεκινά στο ένα από τα δύο σημεία, πηγαίνει αναγκαστικά κάτω από την επιφάνεια της σφαίρας, φτάνει σε ένα μέγιστο βάθος στο μέσον της απόστασης, και έπειτα πλησιάζει την επιφάνεια ξανά και φτάνει στο άλλο σημείο. Αλλά το πρόβλημα με αυτή την ιδέα είναι οτι αυτή η γραμμή πρέπει να βυθιστεί κάτω από την επιφάνεια, πρέπει να αφήσει την επιφάνεια. Όταν λέμε «ο χώρος είναι κυρτός, όπως η επιφάνεια μιας σφαίρας» εννοούμε οτι το σύνολο του χώρου είναι η σφαιρική επιφάνεια· δεν υπάρχει “έξω” για να πάμε, ούτε επιτρέπεται να βυθιστούμε μέσα στη σφαίρα. Επομένως, εάν είναι κανείς αναγκασμένος να μείνει στην επιφάνεια της σφαίρας, ποιο είναι τότε το συντομότερο μονοπάτι που ενώνει δύο σημεία; Η απάντηση είναι οτι πρόκειται για μια γραμμή που μοιάζει με ένα “μέγιστο κύκλο”, ή “ισημερινό” της σφαίρας. Αυτό είναι μια “ευθεία γραμμή” μέσα στο χώρο αυτόν, αφού είναι σύμφωνη με τον αρχικό ορισμό μας: είναι το συντομότερο μονοπάτι που συνδέει τα δύο σημεία. (Γιατί “συντομότερο”; Επειδή αν οδηγήσετε ένα αυτοκίνητο από το ένα σημείο στο άλλο, θα ξοδέψετε το λιγότερο ποσό καυσίμου, δηλαδή ενέργεια, ταξιδεύοντας κατά μήκος αυτής της παρόμοιας με ισημερινό γραμμής που συνδέει τα δύο σημεία· κάθε άλλη διαδρομή θα σας ανάγκαζε να ξοδέψετε περισσότερο καύσιμο.) Προς αποφυγή της σύγχυσης, αντί για “ευθείες γραμμές”, οι μαθηματικοί κάνουν λόγο για “γεωδαισιακές”, που όταν ο χώρος είναι επίπεδος συμπίπτουν με ευθείες γραμμές όπως τις φανταζόμαστε συνήθως· αλλά πάνω σε σφαίρα οι γεωδαισιακές είναι κύκλοι σαν ισημερινοί. Κάθε επιφάνεια, επίπεδη ή κυρτή, έχει γεωδαισιακές γραμμές.
Τώρα, είναι επίπεδος ο οικείος-μας χώρος των τριών διαστάσεων; Μέχρι την εποχή του Αϊνστάιν, πριν δηλαδή εκείνος προτείνει τη γενική σχετικότητα, ο κόσμος έτσι νόμιζε· αλλά στην πραγματικότητα ο χώρος δεν είναι ακριβώς επίπεδος. Είναι περίπου επίπεδος, ειδικά σ’ εκείνα τα μέρη όπου τα αντικείμενα με πολύ μεγάλη μάζα είναι μακριά· αλλά εκεί όπου βρίσκονται αντικείμενα με πολύ μεγάλη μάζα — όπως ένας αστέρας, ο Ήλιος-μας για παράδειγμα — ο χώρος είναι καμπύλος στη γειτονιά αυτών των αντικειμένων. Και όταν ο χώρος είναι καμπύλος, οι “ευθείες γραμμές” (οι γεωδαισιακές) είναι συνήθως οτιδήποτε άλλο εκτός από ευθείες — τουλάχιστον ευθείες με τον τρόπο με τον οποίο συνήθως τις φανταζόμαστε.
Συμβαίνει λοιπόν οτι οι τροχιές των πλανητών είναι γεωδαισιακές, αλλά στον τετραδιάστατο χωροχρόνο-μας, δηλαδή στο συνεχές που περιλαμβάνει τις τρείς διαστάσεις του χώρου συν αυτή του χρόνου, και μέσα στο οποίο υπάρχουν τα πάντα που γνωρίζουμε στο μακρόκοσμο. Σ’ αυτό το τετραδιάστατο συνεχές, οι πλανητικές τροχιές είναι “ευθείες γραμμές”. Η νόησή μας δεν μας επιτρέπει να αντιληφθούμε και τις τέσσερις διαστάσεις ως χωρικές (με ιδιότητες χώρου), οπότε αυτό που βλέπουμε είναι η προβολή της τετραδιάστατης τροχιάς ενός πλανήτη πάνω στον οικείο τριδιάστατο χώρο, στον οποίο στρεβλώνεται, και εμφανίζεται σαν έλλειψη.
Το οτι οι προβολές μπορούν να στρεβλωθούν είναι κάτι το οικείο στον καθένα. Σκεφτείτε τη σκιά της πορείας ενός αεροπλάνου στην επιφάνεια της Γης (δείτε την επόμενη εικόνα).
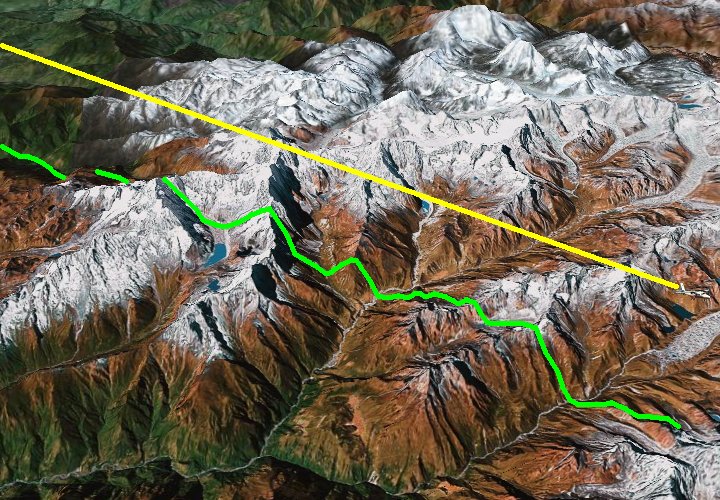
Εικόνα 0.6. Η πορεία ενός αεροπλάνου (κίτρινη ευθεία γραμμή) και η προβολή-της (σκιά, πράσινη) επί ενός ορεινού τοπίου
Παρόλο που το αεροπλάνο πετάει κατά μήκος μιας ευθείας γραμμής σε ένα τριδιάστατο χώρο, η προβολή-του (δηλαδή η σκιά-του) πάνω στη διδιάστατη επιφάνεια της γης(1) ακολουθεί τα χαμηλώματα των κοιλάδων και πεδιάδων, και τα υψώματα των λόφων και βουνών. Αν ήμασταν ανίκανοι να αντιληφθούμε το ανεβοκατέβασμα σαν μια άλλη (3η) χωρική διάσταση επί ίσοις όροις με τις άλλες δύο, αλλά το μόνο που μπορούσαμε να δούμε ήταν η σκιά του αεροπλάνου πάνω στη διδιάστατη επιφάνεια της Γης καθώς η σκιά κινείται πάνω–κάτω, θα νομίζαμε οτι η διδιάστατη πορεία του αεροπλάνου είναι αρκετά πολύπλοκη. Αυτό ακριβώς είναι που συμβαίνει με τις τροχιές των πλανητών: δεν μπορούμε να αντιληφθούμε την τέταρτη διάσταση (το χρόνο) απλά σαν άλλη μία χωρική διάσταση, οπότε αυτό που βλέπουμε είναι ελλειπτικές τροχιές. Ωστόσο, εάν ήμασταν σε θέση να δούμε σε τέσσερις διαστάσεις χωρίς τις αντιληπτικές παρωπίδες-μας, οι τροχιές των πλανητών θα εμφανίζονταν ακριβώς σαν ευθείες όπως η πορεία του αεροπλάνου στις τρεις διαστάσεις.
Από παράδειγμα σε παράδειγμα, βλέπουμε το ίδιο μοτίβο: παρόλο που ο κόσμος είναι απλούστερος απ’ ότι φανταζόμαστε, εμείς εξελιχθήκαμε ώστε να αντιλαμβανόμαστε μια πολυπλοκότητα· και είναι μόνο μέσω των δυνάμεων της διανόησης που καταφέρνουμε να γενικεύουμε και να κατανοούμε την απλότητα που πραγματικά υπάρχει. Στην περίπτωση των πλανητικών τροχιών, επίσης, υπάρχει ένας εξελικτικός λόγος που εξηγεί γιατί είμαστε φτιαγμένοι με τέτοιον τρόπο ώστε να αντιλαμβανόμαστε ως χώρο μόνο τρεις από τις συνολικά τέσσερις μακρο-διαστάσεις.(2) Αυτή η εξελικτική εξήγηση είναι το κυρίως θέμα σε ότι ακολουθεί, από το οποίο θα αποδειχτεί η ομοιομορφία μεταξύ χώρου και χρόνου· οπότε τότε ο χρόνος θα σταματήσει. Στη συνέχεια, θα εξαφανιστείτε.
1. Χρόνος = Χώρος
Ας προχωρήσουμε τώρα για να δείξουμε στην παρούσα ενότητα οτι ο χρόνος είναι ουσιαστικά χώρος, και οτι η νόησή μας είναι που περιπλέκει την κατάσταση, κάνοντάς μας να αντιληφθούμε τις δύο οντότητες σαν πολύ διαφορετικές μεταξύ-τους.
1.1 Το μυστήριο της εξαφάνισης του “πριν” και του “μετά” στη φυσική
Οι φυσικοί έχουν από καιρό παρατηρήσει οτι παρόλο που η καθημερινή-μας εμπειρία μας λέει οτι το παρελθόν είναι πολύ διαφορετικό από το μέλλον, δεν υπάρχει τίποτα στους νόμους της φυσικής — όπως τους ξέρουμε από την εποχή του Γαλιλαίου — που να υποδεικνύει κάποια μορφή ασυμμετρίας μεταξύ του “πριν από τώρα” και του “μετά από τώρα”. Οι νόμοι της φυσικής είναι συμμετρικοί ως προς το χρόνο. Για παράδειγμα, ο Brian Greene (Μπράιαν Γκριν) γράφει στο Τhe Fabric of the Cosmos:[1]
«Τελικά αποδεικνύεται οτι οι γνωστοί και αποδεκτοί νόμοι της φυσικής δεν δείχνουν κάποια [χρονική] ασυμμετρία […]: κάθε κατεύθυνση στο χρόνο, προς τα εμπρός και προς τα πίσω, αντιμετωπίζεται από τους νόμους αδιακρίτως. Και αυτή είναι η απαρχή ενός μεγάλου μυστηρίου. Τίποτα στις εξισώσεις της θεμελιώδους φυσικής δεν δείχνει κάποιο σημάδι αντιμετώπισης της μιας κατεύθυνσης στο χρόνο διαφορετικά από την άλλη, και αυτό βρίσκεται σε πλήρη αντίθεση με ότι βιώνουμε.» (σ. 13, η έμφαση ανήκει στο πρωτότυπο.)
Αυτό που ενοχλεί τους φυσικούς σαν τον Greene είναι το εξής: νιώθουν οτι αν εμείς, οι άνθρωποι, έχουμε κάποιον τρόπο διάκρισης ανάμεσα στο παρελθόν και στο μέλλον, τότε θα έπρεπε να υπάρχει κάτι στους νόμους της φυσικής που να δείχνει οτι αυτό είναι δυνατό. Έλα όμως που δεν υπάρχει!(3) Για τον τυπικό φυσικό, ο ανθρώπινος εγκέφαλος είναι ένας φυσικός μηχανισμός, μια συσκευή, ένα μαραφέτι που υπόκειται στους νόμους της φυσικής, και αυτό το μαραφέτι προφανώς έχει κάποιον τρόπο να διακρίνει μεταξύ του “πριν από τώρα” και του “μετά από τώρα”. Γιατί όμως δεν έχουμε ανακαλύψει κάποιους φυσικούς νόμους που επίσης να διακρίνουν ανάμεσα στο “πριν από τώρα” και στο “μετά από τώρα”, ώστε να μπορούμε να πούμε: «Αχά! Μάλλον ο ανθρώπινος (ή κι ο ζωικός) εγκέφαλος χρησιμοποιεί αυτόν το νόμο, οπότε έτσι είναι που ξεχωρίζει μεταξύ παρόντος και μέλλοντος!»; Ποιο φυσικό νόμο χρησιμοποιεί ο εγκέφαλος (το φυσικό αντικείμενο, το “μαραφέτι”!) που δεν τον ξέρουμε ακόμα; Δεν είναι αυτό μυστήριο;
Ενδεχομένως ο αναγνώστης να αναρωτιέται τί ακριβώς σημαίνει η φράση: «Οι νόμοι της φυσικής είναι συμμετρικοί ως προς το χρόνο». Ιδού μια εξήγηση: Υποθέστε οτι παρατηρείτε ένα αντικείμενο κινούμενο από το σημείο Α στο σημείο Β, με ταχύτητα υ = 1 m/sec. Το αντικείμενο φτάνει στο Β μετά από 1 sec. Συνεπώς η απόσταση ανάμεσα στα Α και Β είναι 1 m. Ο τύπος που σχετίζει τον χώρο s, τον χρόνο t, και την ταχύτητα υ, είναι γνωστός από την εποχή του Γαλιλαίου και τον μαθαίνουμε στο λύκειο: s = υ t (αντικαταστήστε τα υ = 1 m/sec και t = 1 sec για να βρείτε οτι s = 1 m). Τώρα, τί θα συνέβαινε αν αυτό το γεγονός εκτελείτο “ανάποδα”; Ήτοι, τί θα γινόταν αν ο χρόνος έτρεχε προς την αντίθετη κατεύθυνση, όπως σε μια παλιομοδίτικη ταινία στην οποία η κατεύθυνση του φιλμ έχει αντιστραφεί, δείχνοντας τους ανθρώπους να περπατούν με την όπισθεν; Τίποτα το ουσιαστικό δεν θα άλλαζε στο φυσικό γεγονός. Θα βλέπαμε το αντικείμενο να πηγαίνει από το Β στο Α, αντί από το Α στο Β. Για να το περιγράψουμε αυτό θα χρησιμοποιούσαμε τον ίδιο τύπο s = υ t, και θα είχαμε την επιλογή να βάλουμε όπου t = -1 sec, και υ = -1 m/sec, (αφού το υ τίθεται με μια αυθαίρετα ορισμένη θετική κατεύθυνση, την οποία σ’ αυτό το παράδειγμα θεωρήσαμε πως είναι από το Α προς το Β), δίνοντας και πάλι s = 1 m. Καμία ουσιώδης αλλαγή δεν έγινε. Για να το πούμε αλλιώς: αν βλέπαμε μια ταινία που έδειχνε ένα αντικείμενο να πηγαίνει από το Α στο Β, και μια άλλη που έδειχνε το αντικείμενο να πηγαίνει από το Β στο Α, δεν θα είχαμε τρόπο να γνωρίζουμε ποια από τις δύο ταινίες γυρίστηκε με το χρόνο να κυλά προς τα μπρος, και ποια με το χρόνο να κυλά προς τα πίσω.
Ο οξυδερκής αναγνώστης μπορεί στο σημείο αυτό να σκέφτηκε οτι όντως υπάρχουν γεγονότα που συμβαίνουν στο μακρόκοσμο (δηλ. στον κόσμο της καθημερινής-μας εμπειρίας) που φαίνεται οτι δεν είναι αντιστρεπτά στο χρόνο. Για παράδειγμα, τα ακέραια αυγά σπάνε, αλλά κανένας ποτέ δεν είδε τα κομμάτια ενός σπασμένου αυγού να επανασυγκολλώνται ως εκ θαύματος, σχηματίζοντας ξανά ένα ακέραιο αυγό. Ο νόμος της φυσικής που περιγράφει τέτοια γεγονότα είναι ο Δεύτερος Νόμος της Θερμοδυναμικής. Αλλά αυτός είναι ένας στατιστικός νόμος, και όχι θεμελιώδης νόμος της φυσικής με την ίδια έννοια όπως είναι ο s = υ t. Πράγματι, οι θεμελιώδεις νόμοι της φυσικής προβλέπουν οτι δεν θα υπήρχε τίποτα το μαγικό αν βλέπαμε ένα σπασμένο αυγό να ξανασχηματίζεται σε άσπαστο. Είναι οι νόμοι των πιθανοτήτων που δίνουν μια αστρονομικά μηδαμινή πιθανότητα να συμβεί ένα τέτοιο γεγονός. Αλλά οι θεμελιώδεις νόμοι της φυσικής δεν μας λένε τίποτα προκειμένου για σπασμένα αυγά. (Διαβάστε αυτή τη σελίδα-μου [στα αγγλικά] για να καταλάβετε γιατί ο δεύτερος θερμοδυναμικός νόμος δεν είναι νόμος της φυσικής, αλλά ένα καθαρά μαθηματικό αποτέλεσμα· δηλαδή δεν απαιτεί πείραμα, ούτε κάποια παρατήρηση της φύσης προκειμένου να περιγραφεί και να κατανοηθεί· μόνο το στατιστικό χειρισμό κάποιων γεωμετρικών τύπων.)
Ωραία. Ώστε «αυτή είναι η απαρχή ενός μεγάλου μυστηρίου», σύμφωνα με τον Greene. Θα δούμε αργότερα, στο παρόν άρθρο, οτι πράγματι είναι αναμενόμενο να αποτελεί μυστήριο για τους φυσικούς, γιατί η ασυμμετρία του χρόνου, και ιδιαίτερα το γεγονός οτι ο χρόνος μοιάζει να έχει κατεύθυνση(4) δεν είναι κάτι που μπορεί να εξηγηθεί αυστηρά μέσα από το πεδίο της φυσικής, όσο αλλόκοτο κι αν ακούγεται αυτό. Η ασυμμετρία του χρόνου είναι ένα στατιστικό αποτέλεσμα του δεύτερου νόμου της θερμοδυναμικής (αυτό είναι καλά κατανοητό από τους φυσικούς), ενώ το οτι μοιάζει να έχει κατεύθυνση είναι μια ψυχολογική (νοητική) εντύπωση(5) (αυτό δεν είναι καλά κατανοητό· συζητώ την εξήγηση για τη φαινομενική κατεύθυνση του χρόνου σ’ αυτή τη σελίδα [στα αγγλικά]). Άρα, αυτό που μοιάζει να είναι μυστήριο για τον Greene, είναι έτσι γιατί το ερώτημά του δεν είναι ερώτημα για φυσικούς, αλλά για νοολόγους. Εκεί βρίσκεται η ουσία του θέματος την οποία το παρόν κείμενο θα επιχειρήσει να εξηγήσει.
1.2 Όποιος έχει βρεθεί σε δύο διαφορετικά μέρη την ίδια χρονική στιγμή να κάνει ένα βήμα μπρος. (Μη σπρώχνεστε!)
Θα ήθελα να σκεφτούμε στα σοβαρά τώρα το πώς ο περιπαικτικός τίτλος αυτού του εδαφίου μπορεί να πραγματοποιηθεί. Αλλά προτού μπορέσουμε να σκεφτούμε το πώς κάτι μπορεί να βρίσκεται σε δύο μέρη ταυτόχρονα, ας σκεφτούμε ένα πολύ απλούστερο επίτευγμα:
Μπορεί κάποιος ή κάτι να βρίσκεται στο ίδιο μέρος σε δύο διαφορετικούς χρόνους;
Ω, μα ελάτε τώρα, αυτό είναι τετριμμένο. Γίνεται όλη την ώρα από κάθε αντικείμενο που ξεκινά από τη θέση Α σε χρόνο t0, στη συνέχεια πάει λίγο μακρύτερα μέχρι μία θέση Β, όπου σταματάει, αλλάζει κατεύθυνση, και επανέρχεται πίσω στο Α σε χρόνο t1. Κάθε μωρό που μαθαίνει να περπατά μπορεί να το κάνει. Γιατί έπρεπε να κάνουμε αυτή την τετριμμένη άσκηση;
Επειδή, παρόλο που μπορεί να το κάνει κάθε μωρό, κανένας ενήλικος, ανεξάρτητα από το πόσο καλά είναι εξοπλισμένος τεχνολογικά, δεν μπορεί να κάνει το αντίθετο: να βρίσκεται σε δύο διαφορετικά μέρη την ίδια στιγμή.
Ασφαλώς όχι. Για υλικά σώματα αυτό απαγορεύεται από τη σχετικότητα: θα έπρεπε κάτι να κινηθεί με την ταχύτητα c του φωτός ώστε να είναι ικανό να πάει από το Α στο Β στον ίδιο χρόνο t0 (σύμφωνα με το σύστημα αναφοράς του κινούμενου αντικειμένου), και κανένα αντικείμενο με μη-μηδενική μάζα δεν μπορεί να το κάνει αυτό, επειδή θα χρειαζόταν ένα άπειρο ποσό ενέργειας ώστε να επιταχύνει το αντικείμενο μέχρι την ταχύτητα c — και άπειρες ενέργειες δεν υφίστανται.
Ακριβώς. Ένα αντικείμενο με μάζα δεν θα ήταν σε θέση να το πετύχει αυτό. Αλλά τί θα λέγατε για ένα σωματίδιο χωρίς μάζα; Ας πούμε, ένα φωτόνιο;
Ένα φωτόνιο όμως δεν είναι παρατηρητής.
Δεν απαιτήσαμε οτι πρέπει να είναι παρατηρητής αυτό που θέλουμε να βρίσκεται σε δύο μέρη κατά τον ίδιο χρόνο. Άρα, φαίνεται οτι ένα φωτόνιο μπορεί να το κάνει. Αλλά εάν επιμείνουμε στο να έχουμε έναν παρατηρητή, τί θα λέγατε αν χαλαρώναμε την προϋπόθεση οτι ο χρόνος t0 πρέπει να είναι ακριβώς ο ίδιος; Τί θα λέγατε αν ζητούσαμε να είναι ένας παρατηρητής σε δύο διαφορετικά μέρη εντός ενός πολύ σύντομου χρονικού διαστήματος, Δt;
Αυτό δεν φαίνεται να είναι καθόλου προβληματικό. Δεδομένου, φυσικά, οτι αν το Δt είναι πολύ μικρό, και το με ιδιότητες-χώρου διάστημα Α-Β επαρκώς μακρύ, τότε η αντίστοιχη ταχύτητα του παρατηρητή πρέπει να είναι πολύ μεγάλη, πολύ κοντά στο c. Και η κινητική-του ενέργεια πρέπει επίσης να είναι υψηλή, αν υποτεθεί οτι ο παρατηρητής κατέχει κάποια ποσότητα μάζας.
Άρα, αυτό είναι όλο. Μπορούμε να έχουμε παρατηρητές που, όταν κινούνται με πολύ μεγάλες ταχύτητες (κοντά στο c), καταφέρνουν να είναι σε δύο μέρη, σχεδόν κατά τον ίδιο χρόνο (σύμφωνα με τα ρολόγια-τους). Ας φανταστούμε έναν τέτοιο υποθετικό κόσμο από ταχύτατα κινούμενους παρατηρητές, κι ας προσπαθήσουμε να κατανοήσουμε με τί θα έμοιαζε ο χώρος και ο χρόνος από τη δική-τους οπτική γωνία.
1.3 Ο κόσμος σύμφωνα με τα πλασμοειδή
Στο παρόν εδάφιο θα προσπαθήσουμε να κατανοήσουμε την αντίληψή μας για τις ιδιότητες του κόσμου που κατοικούμε δημιουργώντας μια αναλογία με έναν υποθετικό κόσμο· έναν κόσμο που αποτελείται από ενεργητικά σωματίδια, και κατοικείται από νοήμονα όντα που τρέχουν σχεδόν με την ταχύτητα του φωτός σε σχέση με αντικείμενα-ορόσημα στο χώρο (π.χ. τα αστέρια). Για χάρη της αποφυγής περιφράσεων, θα ονομάσω τα όντα αυτά πλασμοειδή.(6) Έτσι, τα πλασμοειδή κινούνται προς μια κατεύθυνση στο χώρο έναντι των μακρινών αστέρων (ας υποθέσουμε οτι ο χωρικός κόσμος-τους αποτελείται από μια μοναδική διάσταση) με σχεδόν την ταχύτητα του φωτός, c. Υποθέτουμε οτι έχουν εξελιχθεί σε αυτόν εδώ τον κόσμο (δηλ. στο σύμπαν-μας), και το ερώτημα είναι πώς φαίνεται να είναι ο κόσμος από τη δική-τους νοητική οπτική γωνία.
Αν τα πλασμοειδή κινούνται στο χώρο με ταχύτητα σχεδόν ίση με c, ο χώρος θα πρέπει να εμφανίζεται σ’ αυτά σαν να “ρέει” προς μία κατεύθυνση. Αν οι ταχύτητές τους θεωρούμε οτι είναι πάντα πολύ κοντά στο c, τότε η αντίληψή τους θα μπορούσε ενδεχομένως να περιλαμβάνει την αίσθηση του οτι δεν έχουν κανέναν έλεγχο πάνω στο πέρασμα του χώρου. Αυτό συμβαίνει επειδή μικροσκοπικές διακυμάνσεις γύρω από την “κανονική-τους” ταχύτητα c, θα είναι ανεπαίσθητες γι’ αυτά. Γιατί; Επειδή έχοντας εξελιχθεί σε ένα κόσμο όπου οι ταχύτητες είναι πάντα πολύ κοντά στο c, τα πλασμοειδή δεν θα έχουν αναπτύξει αισθητήρες για τις πολύ μικρές διαφορές στην ταχύτητα του χώρου “που περνάει”, επειδή τέτοιες διαφορές, όντας μικροσκοπικές, δεν θα τα βοηθούσαν μέσω φυσικής επιλογής έναντι άλλων ειδών στο περιβάλλον-τους. Ένας τρόπος να το καταλάβουμε αυτό είναι με το να αντιστρέψουμε την αναλογία και να την εφαρμόσουμε στον οικείο-μας κόσμο. Εμείς, η πανίδα του πλανήτη Γη, δεν αναπτύξαμε αισθητήρες για τις διαφορές με τις οποίες ο χρόνος ρέει, επειδή — λόγω των εξαιρετικά αργών (ως προς το c) ταχυτήτων-μας μέσα στον περιβάλλοντα κόσμο — οι διαφορές αυτές δεν παρέχουν κάποιο πλεονέκτημα επιβίωσης. Εντούτοις, υπάρχουν: το ρολόι ενός παρατηρητή που κινείται στην επιφάνεια της Γης τρέχει ελαφρώς βραδύτερα απ’ ότι ένα συγχρονισμένο μ’ αυτό στάσιμο ρολόι. Αυτές οι διαφορές, ωστόσο, είναι τόσο μικροσκοπικές που είναι βιολογικά αδύνατο για ένα ζώο να εξελιχθεί με τέτοιου είδους αισθητήρες και να τους χρησιμοποιήσει προς όφελός του.
Υπάρχει πλήθος τέτοιων παραδειγμάτων στο βιολογικό κόσμο. Πάρτε για παράδειγμα την όραση με ακτίνες-Χ. Παρόλο που ο κύριος όγκος της ηλεκτρομαγνητικής ακτινοβολίας που φτάνει την επιφάνεια της Γης ανήκει στο ορατό φάσμα, όπως ήδη σημειώσαμε στην §0.2, υπάρχει μία πολύ μικρή ποσότητα ακτινοβολίας από ολόκληρο το υπόλοιπο φάσμα, συμπεριλαμβανομένων και των ακτίνων-Χ. Θεωρητικά θα ήταν πλεονέκτημα να μπορεί κανείς να δει μέσω ακτίνων-Χ — ζώα με ένα τέτοιο οπτικό σύστημα θα ήσαν ικανά να βλέπουν διαμέσου αντικειμένων που σε άλλα ζώα θα έμοιαζαν αδιαφανή. Παρ’ όλα αυτά, μόνο και μόνο επειδή οι ακτίνες-Χ δίνουν ένα πλεονέκτημα, δεν σημαίνει και οτι πρέπει να έχει εξελιχτεί ένας βιολογικός μηχανισμός που να εκμεταλλεύεται αυτό το πράγμα. Δεν αποτελεί κάθε φυσικό χαρακτηριστικό μια βιολογική πιθανότητα.(7) Ακριβώς όπως κανένα πλάσμα δεν εξελίχθηκε να βλέπει με ακτίνες-Χ, παρομοίως, κανένα πλάσμα πάνω στον πλανήτη-μας δεν εξελίχθηκε ώστε να αντιλαμβάνεται μικροσκοπικές διαφορές στην ταχύτητα της ροής του χρόνου. Κατ’ αναλογία λοιπόν, φαίνεται λογικό να υποθέσουμε οτι και τα πλασμοειδή του πειράματος σκέψης-μας στερούνται την ικανότητα να ανιχνεύουν μικροσκοπικές διαφορές στη ροή του χώρου.
Τώρα, μπορεί να ισχυριστεί κανείς οτι τα πλασμοειδή θα μπορούσαν εντούτοις να αναπτύξουν τέτοιους αισθητήρες. Εμείς, άλλωστε, έχουμε ανιχνευτές κίνησης στον εγκέφαλό μας, που ανιχνεύουν την παραμικρή κίνηση (αλλαγή συντεταγμένων) των αντικειμένων στο χώρο· επομένως, γιατί τάχα πρέπει τα πλασμοειδή να στερούνται έναν τέτοιο μηχανισμό, αφού ένας παρόμοιος μηχανισμός είναι αποδεδειγμένα φυσικώς δυνατός; Η απάντηση είναι οτι εμείς οι άνθρωποι συγκρίνουμε τις νέες χωρικές συντεταγμένες κινούμενων αντικειμένων έναντι του μηδενός, δηλ., έναντι της σχετικής ακινησίας άλλων κοντινών αντικειμένων· ενώ τα πλασμοειδή θα έπρεπε να αισθανθούν μια διαφορά σε χωρικές συντεταγμένες έναντι ενός υποβάθρου συντεταγμένων που αλλάζουν με τον ρυθμό της ταχύτητας του φωτός c — που είναι μια τεράστια(8) σταθερά. Κάθε μικρή απόκλιση από το c “πνίγεται” από το μέγεθος αυτής της σταθεράς, που κάνει την ανίχνευση τέτοιων αποκλίσεων δύσκολη. Θα ήταν σαν να προσπαθεί κανείς ν’ αντιληφθεί ψίθυρο κοντά στo λειτουργούντα κινητήρα ενός αεροπλάνου. Ωστόσο, ο αναγνώστης μπορεί ν’ αντιτάξει οτι το c εμφανίζεται τεράστιο μόνο σ’ εμάς, ενώ για τα πλασμοειδή το c θα μπορούσε, κατά συμμετρικό τρόπο, να παίζει το ρόλο του “μηδέν”. Αλλά το c είναι αντικειμενικά διαφορετικό από το μηδέν: είναι η σταθερά εκείνη που ορίζει την έννοια του ταυτόχρονου στο σύμπαν-μας, μέσω της σχέσης s = c·t, όπως επίσης η σταθερά που καθορίζει την ισοδυναμία μάζας και ενέργειας, μέσω του E = m·c2. Το μηδέν, προφανώς, δεν έχει τέτοιες ιδιότητες.
Υποθέτοντας οτι τα πλασμοειδή δεν εξελίχθηκαν με μηχανισμούς ώστε να αντιλαμβάνονται τις μικροσκοπικές διαφορές στη ροή του χώρου, τί γίνεται με την αντίληψή τους του χρόνου; Θα ένιωθαν άραγε οτι μπορούν να κατευθυνθούν πίσω κα μπρος στο χρόνο, όπως εμείς έχουμε την ανάλογη αίσθηση για το χώρο; Προκειμένου να επιτραπεί η προς τα πίσω κίνηση στο χρόνο — αν και σε πολύ μικρό βαθμό — πρέπει να υποθέσουμε μία επιπλέον ιδιότητα για τα πλασμοειδή. Φυσιολογικά εμείς, οι παρατηρητές–άνθρωποι, αντιλαμβανόμαστε για τους εαυτούς-μας οτι αποτελούμαστε από ένα μεγάλο ποσό αδρανούς μάζας, και πολύ λίγη κινητική ενέργεια: αντιλαμβανόμαστε τους εαυτούς-μας ως συνήθως ακίνητους σε σχέση με το περιβάλλον-μας. Μπορούμε ωστόσο να παραγάγουμε λίγη κινητική ενέργεια ξοδεύοντας ένα ελάχιστο ποσό της μάζας-μας (μια διαδικασία που υλοποιείται στα μιτοχόνδρια των κυττάρων-μας), και με τον τρόπο αυτό αισθανόμαστε οτι μπορούμε να κινηθούμε στο χώρο προς οποιαδήποτε κατεύθυνση, αν και σε πολύ αργές ταχύτητες σε σχέση με το c. Παρόμοια, τα πλασμοειδή θα μπορούσαν να μετατρέψουν ένα μικρό ποσό της κινητικής-τους ενέργειας σε αδρανειακή μάζα (που πλέον θα καλούνται, αντιστοίχως, απλά ενέργεια και μάζα, εγκαταλείποντας τους επιθετικούς προσδιορισμούς χάριν απλότητας) μειώνοντας έτσι, κατά κάτι λίγο, την ταχύτητά τους. Ωστόσο, ο μεταβολισμός-τους τους επιτρέπει επίσης να κάνουν το αντίστροφο: να μειώσουν τη μάζα-τους στο μηδέν, μετατρέποντάς την όλη σε ενέργεια, ώστε να κινούνται ακριβώς με την ταχύτητα του φωτός. (Κατ’ αναλογία, εμείς μπορούμε να ελαττώσουμε την ενέργειά μας στο μηδέν, φτάνοντας σε ακινητοποίηση.) Επιπλέον, μπορούν να περάσουν στην “άλλη πλευρά” του φάσματος μάζα–ενέργεια, αποκτώντας μια πολύ μικρή ποσότητα φανταστικής και αρνητικής μάζας και ενέργειας, και μια ταχύτητα ελαφρώς μεγαλύτερη από το c.(9) Το οτι αποκτούν τέτοιες εξωτικές ιδιότητες όπως η φανταστική και αρνητική μάζα και ενέργεια είναι μια συνέπεια του σχετικιστικού τύπου:
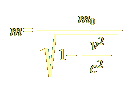
Όπου, εάν v > c, η ποσότητα στον παρονομαστή γίνεται φανταστική, ώστε το κλάσμα γίνεται ανάλογο του m0/i, και αφού 1/i = -i, αποκτούμε έτσι φανταστική και αρνητική μάζα m. Η ενέργεια ακολουθεί το παράδειγμα της μάζας, λόγω του E=m·c2. Τώρα, για να καταλάβουμε πώς τα πλασμοειδή καταφέρνουν να επιτύχουν μικρές μετατοπίσεις στο χρόνο, είναι χρήσιμο να εξετάσουμε πώς εμείς μπορούμε να εκτελέσουμε μετατοπίσεις στο χώρο. Το κάνουμε αυτό με το να κινούμαστε από ένα μέρος σε ένα άλλο, μετρώντας το χρόνο t (τον οποίο δεν ελέγχουμε) που χρειάστηκε για να μετακινηθούμε. Το πηλίκο του χώρου s διά του χρόνου t το καλούμε ταχύτητα.(10) Παρόμοια, τα πλασμοειδή θα μπορούσαν να αποφασίσουν να κινηθούν “προς τα εμπρός” στο χρόνο (σε σχέση με το χρονικό σύστημα αναφοράς στο οποίο βρίσκονται “τώρα”) αυξάνοντας ελάχιστα τη μάζα-τους, και ως εκ τούτου μειώνοντας την ενέργεια και την ταχύτητά τους — παραμένοντας όλο αυτό το διάστημα στην περιοχή του c και της μέγιστης ενέργειας(11) που μπορούν να αποκτήσουν. Μπορούν να επιταχυνθούν με το να μειώσουν την μάζα-τους. Όταν η μάζα γίνεται μηδέν, επιτυγχάνουν τη μέγιστη ενέργειά τους και την ταχύτητα c, και τότε μπορούν να προχωρήσουν λίγο “προς τα πίσω” στο χρόνο με περαιτέρω επιτάχυνση, αποκτώντας φανταστική–αρνητική μάζα και ενέργεια — παραμένοντας πάντα στην περιοχή του c. Σημειώστε οτι αν τα πλασμοειδή φυσιολογικά δεν μπορούν να διακρίνουν μεταξύ κανονικής και φανταστικής–αρνητικής μάζας και ενέργειας, αντιλαμβάνονται επίσης μια τέλεια συμμετρία μεταξύ της “προς τα εμπρός” και της “προς τα πίσω” κίνησης στο χρόνο· για τα πλασμοειδή, πρόκειται απλά για κίνηση προς αυτή ή προς εκείνη τη χρονική κατεύθυνση.
1.4 Θα μπορούσαν η διαστολή του χρόνου και η συστολή του μήκους να σπάσουν τη συμμετρία;
Μέχρι στιγμής έχουμε κατασκευάσει μια οπτική κατά την οποία οι έννοιες του χώρου και της μάζας βρίσκονται σε πλήρη συμμετρία με τις έννοιες του χρόνου και της ενέργειας. Το θέμα φαίνεται να εξαρτάται από το σε ποια πλευρά του φάσματος μάζα–ενέργεια έχει κανείς το μεγαλύτερο μέρος της ύπαρξής του. Αλλά τί γίνεται με τις σχετικιστικές έννοιες της διαστολής του χρόνου και της συστολής του μήκους; Δεν είναι μήπως οι διαφορετικές αυτές έννοιες, διαστολή έναντι συστολής, όπως αρχικά περιγράφηκαν στη σημαίνουσα δημοσίευση του Αϊνστάιν,[2] που υποδεικνύουν μια θεμελιώδη διαφορά μεταξύ χώρου και χρόνου; Στο κάτω-κάτω, ο χρόνος είναι που διαστέλεται, δεν συστέλλεται· αντίθετα, η έννοια της συστολής εφαρμόζει στο χώρο, και καθώς διαστολή και συστολή είναι έννοιες αντίθετες μεταξύ-τους, μήπως μας δίνουν ένα μέσο για ν’ αποφασίσουμε ποια διάσταση είναι ο χώρος, και ποια είναι ο χρόνος; Ίσως να μπορούμε να πούμε οτι η διάσταση που διαστέλλεται είναι ο χρόνος, ενώ εκείνη που συστέλλεται είναι ο χώρος. Σ’ αυτή την υποενότητα θα διαπιστώσουμε οτι η συμμετρία μεταξύ χώρου και χρόνου επιμένει να υφίσταται· δηλαδή αυτό που εμάς μας φαίνεται σαν διαστολή, στα πλασμοειδή πρέπει να εμφανίζεται σαν συστολή, και αντιστρόφως. (Αν διστάζετε να ακολουθήσετε τις τεχνικές λεπτομέρειες που ακολουθούν, μπορείτε να με πιστέψετε οτι η συμμετρία παραμένει, και να προχωρήσετε στην επόμενη υποενότητα.)
Ας εξετάσουμε τις έννοιες της διαστολής και της συστολής από την οπτική γωνία των πλασμοειδών. Όπως αναφέρθηκε, τα πλασμοειδή δεν αντιλαμβάνονται άμεσα την κίνηση στο χώρο. Εντούτοις, οι φυσικοί-τους μπορούν να βεβαιώσουν τους μη-ειδήμονες μεταξύ των πλασμοειδών οτι τα όργανά τους μετρούν μια “διαστολή (επέκταση) του χώρου” για κάθε παρατηρητή O2 που αλλάζει τις χρονικές συντεταγμένες-του ως προς έναν άλλο παρατηρητή O1. Ιδού γιατί.
 |
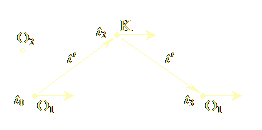 |
| Εικόνα 1.1α | Εικόνα 1.1β |
Θεωρείστε τον πλασμοειδή παρατηρητή O1, του οποίου η χρονική συντεταγμένη είναι t0 (Εικ. 1.1α). Ο O1 στέλνει ένα φωτόνιο προς το γεγονός K. Το φωτόνιο ταξιδεύει για συνολικό χρόνο t (κατά την άποψη του O1), αντανακλάται μόλις φτάσει στο γεγονός K κατά το χρόνο t1, ταξιδεύει προς τα πίσω, και φτάνει στον O1 κατά τη χρονική συντεταγμένη t0 (επειδή ο O1 παραμένει ακίνητος στο χρόνο). Ο O1 υπολογίζει οτι το φωτόνιο ταξίδεψε για συνολική χρονική απόσταση 2t. Επομένως ο χώρος s που διανύθηκε όσο το φωτόνιο έκανε αυτό το ταξίδι είναι s = 2ct. Τώρα ας θεωρήσουμε την Εικ. 1.1β, που δείχνει την ίδια ακολουθία γεγονότων, αλλά από την οπτική γωνία ενός δεύτερου πλασμοειδούς παρατηρητού, του O2, που κινείται ομοιόμορφα στο χρόνο ως προς τον παρατηρητή O1, και ο οποίος, συνεπώς, αντιλαμβάνεται τον O1 και το K να αλλάζουν τις χρονικές συντεταγμένες-τους με ομοιόμορφο τρόπο, καθώς ο χώρος περνάει. Ο O2 σημειώνει οτι το φωτόνιο αφήνει τον O1 κατά το χρόνο t0, φτάνει στο K κατά το χρόνο t2, έχοντας προηγουμένως διανύσει μια συνολική χρονική απόσταση t' > t, αντανακλάται στο K, και επιστρέφει στον O1, που βρίσκεται τώρα σε διαφορετική χρονική συντεταγμένη, t3. Η συνολική χρονική απόσταση κατά τον O2 είναι 2t', που είναι μεγαλύτερη από το 2t. Ο O2 υπολογίζει το συνολικό χώρο που παρεμβλήθηκε από το σημείο του πρώτου γεγονότος κατά το t0 μέχρι το σημείο του δεύτερου γεγονότος στο t3, και βρίσκει οτι αυτός ισούται με s' = 2ct' > 2ct = s. Άρα ο O2 υπολογίζει μια μεγαλύτερη τιμή s' > s για το χώρο, και υποστηρίζει οτι ο χώρος του κινούμενου παρατηρητή O1 “διαστέλλεται”.
Αν τα πλασμοειδή παρατηρούν διαστολή του χώρου, τότε — λόγω συμμετρίας — υποπτευόμαστε οτι επίσης παρατηρούν συστολή του χρόνου. Πράγματι, ας υποθέσουμε οτι οι πλασμοειδείς παρατηρητές O1 και O2 κινούνται με την ίδια ταχύτητα v ως προς έναν τρίτο πλασμοειδή παρατηρητή O, ο οποίος θέλει να υπολογίσει τη διαφορά στις χωρικές συντεταγμένες μεταξύ των O1 και O2 (Εικ. 1.2α).
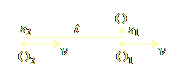 |
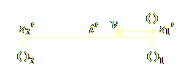 |
| Εικόνα 1.2α | Εικόνα 1.2β |
Ας υποθέσουμε οτι ο O1 φτάνει πρώτος στη χρονική συντεταγμένη t0 του O, οπότε ο O σημειώνει τη χωρική συντεταγμένη s1 του O1 όταν καί οι δυο-τους βρίσκονται στην ίδια χρονική συντεταγμένη. Λίγο χώρο αργότερα, ο O2 φτάνει στη χρονική συντεταγμένη του O (που είναι πάντα t0), και ο O σημειώνει το νέο χώρο s2 όπου συνέβη αυτή η συνάντηση. Ο O υπολογίζει τη συνολική χρονική διαφορά μεταξύ των O1 και O2: t = (s2 - s1) / v (Ισότητα 1). Τώρα ας θεωρήσουμε την κατάσταση στην Εικ. 1.2β, που είναι παρόμοια με εκείνη της Εικ. 1.2α, μόνο που τώρα ο O είναι που κινείται με ταχύτητα v, και ταξιδεύει από τη χρονική συντεταγμένη του O1 προς τη χρονική συντεταγμένη του O2, προτιθέμενος να μετρήσει τη μεταξύ-τους χρονική διαφορά. Ο O βρίσκεται στη χρονική συντεταγμένη του O1 στο σημείο του χώρου s1', και φτάνει στη χρονική συντεταγμένη του O2 στο σημείο του χώρου s2'. Ο O υπολογίζει τη συνολική χρονική διαφορά μεταξύ των O1 και O2 ως: t' = (s2' - s1') / v (Ισότητα 2). Από τις ισότητες 1 & 2, απαλείφοντας το v, παίρνουμε: (s2 - s1) / t = (s2' - s1') / t', επομένως: t = t' (s2 - s1) / (s2' - s1') (Ισότητα 3). Είδαμε στην προηγούμενη παράγραφο οτι ο χώρος του O πρέπει να “διασταλεί” στην κατάσταση της Εικ. 1.2β, επομένως συμπεραίνουμε οτι s2 - s1 < s2' - s1'. Άρα, από την Ισότητα 3, συμπεραίνουμε οτι t < t', που σημαίνει οτι ο O παρατηρεί τη χρονική διαφορά t των παρατηρητών O1 και O2 στην Εικ 1.2α να έχει “συσταλεί” ως προς τη διαφορά-τους t' που υπολογίστηκε στο αδρανειακό σύστημα αναφοράς της Εικ. 1.2β.
Τα προηγούμενα αποτελέσματα, βέβαια, είναι αναμενόμενα λόγω της εναλλαγής των ρόλων μεταξύ των εννοιών “χώρος” και “χρόνος” στον κόσμο των πλασμοειδών. Αυτό που δείχνει η παρούσα υποενότητα είναι οτι ακόμα και οι οικείες-μας σχετικιστικές έννοιες της διαστολής του χρόνου και της συστολής του χώρου, στην πραγματικότητα δεν υποδεικνύουν κάποια θεμελιώδη διαφορά μεταξύ χώρου και χρόνου. Αυτό που εμείς ονομάζουμε “διαστολή”, τα πλασμοειδή θα το ονόμαζαν “συστολή”, και αντιστρόφως. Δεν υπάρχει κάποιο χαρακτηριστικό που να μπορεί να αποδοθεί στο χώρο ή στο χρόνο ώστε να διαχωρίσει τον έναν από τον άλλο.
Το τί ονομάζουμε “χώρο” και τί “χρόνο” είναι έννοιες σχετικές — αυτό είναι το τελικό συμπέρασμα· σχετικές, δηλαδή, με τη σύσταση σε μάζα–ενέργεια του παρατηρητή.
1.5 Θα μπορούσε να ισχύει οτι στην πραγματικότητα ταξιδεύουμε ταχύτατα στο χρόνο;
Ο υποθετικός κόσμος των πλασμοειδών μας λέει οτι ακόμα και αν οι χωρικές και χρονικές διαστάσεις του κόσμου-μας είναι αντικειμενικά παρόμοιες μεταξύ-τους (όπως μας πληροφορούν οι νόμοι της φυσικής), ο τρόπος με τον οποίο γίνονται αντιληπτές από νοήμονα όντα που υπάρχουν σ’ αυτές εξαρτάται από τη συγκεκριμένη σχέση που τα όντα έχουν με κάθε διάσταση. Τα πλασμοειδή, ζώντας στο πλούσιο σε ενέργεια άκρο του φάσματος μάζα–ενέργεια, υποτιθέμενα εξελίχθηκαν να αντιλαμβάνονται μικρές μετατοπίσεις στο χρόνο, αλλά να αισθάνονται οτι ο χώρος “κυλάει”, σε μια αδυσώπητη πορεία από περιοχές που πρόκειται να ανακύψουν, προς περιοχές που αφήνονται πίσω. Τα ανθρώπινα όντα, που ζουν στην αντίθετη, πλούσια σε μάζα πλευρά του φάσματος, εξελίχθηκαν να αντιλαμβάνονται μικρές μετατοπίσεις στο χώρο, αλλά να αισθάνονται οτι ο χρόνος “κυλάει”, σε μια αδυσώπητη πορεία από γεγονότα που πρόκειται να βιωθούν, προς γεγονότα που μένουν στην ανθρώπινη μνήμη.
Ένα ερώτημα που μπορεί να τεθεί σ’ αυτό το σημείο είναι το ακόλουθο: αν τα πλασμοειδή κινούνται μέσα στο χώρο σε σχέση με χωρικά ορόσημα, δεν θα μπορούσαμε και εμείς να θεωρηθούμε σαν να “κινούμαστε στο χρόνο”, και μάλιστα σχεδόν με την ταχύτητα του φωτός c;(12) Ας δούμε τί έχουν να πουν οι ειδικοί πάνω στο θέμα. Σύμφωνα με τον Greene:[1]
«Η ειδική σχετικότητα δηλώνει ένα […] νόμο για όλη την κίνηση: το άθροισμα της ταχύτητας της κίνησης οποιουδήποτε αντικειμένου στο χώρο και της κίνησής του στο χρόνο είναι πάντα ακριβώς ίσο με την ταχύτητα του φωτός. Στην αρχή μπορεί ενστικτωδώς να αναπηδήσετε από αυτή τη δήλωση, αφού όλοι είμαστε συνηθισμένοι στην ιδέα οτι μόνο το φώς μπορεί να κινηθεί με την ταχύτητα του φωτός. Αλλά αυτή η οικεία ιδέα αναφέρεται μόνο στην κίνηση στο χώρο. Τώρα αναφερόμαστε σε κάτι σχετικό, αλλά πλουσιότερο: τη συνδυασμένη κίνηση ενός αντικειμένου στο χώρο και στο χρόνο. Το βασικό γεγονός, που βρήκε ο Αϊνστάιν, είναι οτι αυτά τα δύο είδη κίνησης είναι πάντα συμπληρωματικά. Όταν το παρκαρισμένο αυτοκίνητο που κοιτούσατε απομακρύνεται, αυτό που πραγματικά συμβαίνει είναι οτι κάποια από τη με-ταχύτητα-φωτός κίνησή του μετατρέπεται από κίνηση στο χρόνο σε κίνηση στο χώρο, διατηρώντας το συνδυασμένο άθροισμα αμετάβλητο. Η εν λόγω μετατροπή σημαίνει οτι η κίνηση του αυτοκινήτου διαμέσου του χρόνου λιγοστεύει.» (σελ. 49, η έμφαση στο πρωτότυπο).
Έτσι, υποθέτοντας οτι η κίνησή μας στο χώρο δεν είναι και τόσο μεγάλη (ακολουθούμε την κίνηση της Γης, η οποία περιφέρεται γύρω από τον Ήλιο, ο οποίος περιφέρεται γύρω από το κέντρο του Γαλαξία, κ.ο.κ), έπεται οτι η κίνησή μας λαμβάνει χώρα πρωτίστως στη διάσταση του χρόνου.
Πρέπει να σημειώσω εδώ πως ένας φυσικός, σχολιαστής ενός προηγούμενου προσχεδίου αυτού του άρθρου (στο οποίο το παραπάνω απόσπασμα του Greene δεν περιλαμβανόταν, παραμόνο μια αναφορά σ’ αυτό), αντέδρασε εντελώς αρνητικά προς την ιδέα της “κίνησης μέσα στο χρόνο”, και τη χλεύασε. Για το φυσικό αυτόν η κίνηση σχετίζεται με την έννοια της ταχύτητας, και ταχύτητα είναι το πηλίκο του χώρου προς το χρόνο, οπότε η κίνηση συμβαίνει αναγκαστικά στο χώρο. Πώς μπορούμε να αντιληφθούμε την κίνηση στο χρόνο; Τί ταχύτητα θα είχε κάτι που κινείται στο χρόνο; Δεν μπορούμε να διαιρέσουμε το χρόνο διά του χρόνου για να βρούμε την ταχύτητα (αν το κάνουμε καταλήγουμε σε ανοησίες), επομένως η όλη ιδέα της κίνησης στο χρόνο είναι ανοησία, σύμφωνα με αυτόν το φυσικό.
Και όμως, πιστεύω οτι αυτό που λείπει είναι μια ελάχιστη νοητική προσπάθεια για να γενικεύσουμε από την έννοια της ταχύτητας όπως τη μάθαμε στο σχολείο (πηλίκο χώρου προς χρόνο) προς μια γενικευμένη έννοια — ας την ονομάσουμε “ρυθμό χωροχρονικής κίνησης”, ή “ρυθμό” για συντομία — η οποία περιλαμβάνει τόσο την οικεία-μας ταχύτητα (χώρος προς χρόνο) όσο και την αντίστροφη έννοια (χρόνος προς χώρο). Ο ρυθμός έχει διττή φύση: όταν εκφράζεται με οικείους-μας όρους (από την ανθρώπινη οπτική), πρόκειται για τη γνωστή-μας ταχύτητα· όταν όμως εκφράζεται με όρους πλασμοειδών, πρόκειται για την αντίστροφη έννοια: χρόνος δια χώρο. Μαθηματικά, μπορούμε να το συμβολίσουμε με το ζευγάρι [v, u] όπου το v είναι η γνωστή-μας ταχύτητα (χώρος προς χρόνο) και το u η μη-οικεία χρονική συνιστώσα (χρόνος προς χώρο). Όσο μεγαλύτερο είναι το v τόσο μικρότερο είναι το u, και αντιστρόφως, έτσι ώστε η σχέση v + u = c να ισχύει πάντα. Ο ρυθμός είναι φυσικά σχετικιστικός, άρα εξαρτάται από τον παρατηρητή, και οι δύο συνιστώσες-του έχουν σαν όριο την ταχύτητα του φωτός, c: μια ακραία τιμή για το ρυθμό είναι η [c, 0], και μια άλλη ακραία τιμή είναι η [0, c]. Έτσι, αν παρατηρήσουμε ένα πλασμοειδές να κινείται με ταχύτητα c (μάζα μηδέν, ενέργεια μέγιστη), ο ρυθμός αυτού του πλασμοειδούς είναι [c, 0]. Παρόμοια, αν είμαστε ακίνητοι σε σχέση με αντικείμενα–ορόσημα (π.χ. αστέρες), τότε έχουμε ρυθμό [0, c]. Πιθανώς να υπάρχει ένας καλύτερος, πιο παραγωγικός φορμαλισμός γι’ αυτή την έννοια του “ρυθμού” — καθώς, ειλικρινά, δεν βλέπω πώς μπορεί κανείς να κάνει χρήσιμη φυσική με ένα μαθηματικό ζεύγος — αλλά η ύπαρξη ή μη-ύπαρξη καλύτερου φορμαλισμού δεν είναι επιχείρημα εναντίον της ύπαρξης της έννοιας καθεαυτής, δηλ. του ρυθμού, όπως περιγράφεται ανωτέρω. Σημειώστε οτι η χρήση της λέξης “κίνηση” στο παρόν χωρίο είναι παραπλανητική. Δεν υπάρχει πραγματικά καμμία κίνηση, εκτός μόνο από μια ακολουθία τετραδιάστατων σημείων (“γεγονότων”) στον τετραδιάστατο χωροχρόνο.
Οπότε, η ερώτηση «Ποια είναι η ταχύτητά μας στο χρόνο;» δεν έχει νόημα αν με το «ταχύτητα» εννοούμε την οικεία-μας έννοια. Αλλά μπορούμε να ρωτήσουμε: «Ποια είναι η χρονική συνιστώσα του ρυθμού-μας όταν είμαστε ακίνητοι σε σχέση με τους αστέρες;» Υποθέτοντας οτι με το «χρονική συνιστώσα» εννοούμε το δεύτερο μέλος του ανωτέρω ζεύγους στην παράσταση του ρυθμού, η απάντηση είναι οτι η χρονική συνιστώσα-μας είναι ίση με c.
Ένας τρόπος να φανταστούμε τα παραπάνω, ο οποίος είναι ποσοτικά λάθος αλλά ποιοτικά σωστός — θα δούμε σε λίγο τί σημαίνει αυτό — δίνεται από την ακόλουθη αναλογία. Υποθέστε οτι έχουμε ένα διδιάστατο χώρο σαν ένα φύλλο χαρτιού, άπειρο προς όλες τις κατευθύνσεις, και αντί να ονομάσουμε τις διαστάσεις x και y όπως συνήθως, τις ονομάζουμε s και t (βλ. Εικόνα 1.3, παρακάτω). Σχεδιάστε ένα κατακόρυφο ευθύγραμμο τμήμα, όπως στην Εικ. 1.3 (a).
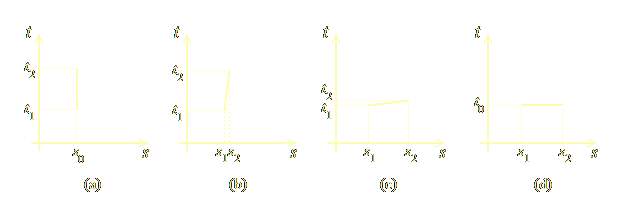
Εικόνα 1.3. Απλοποίηση της έννοιας της κίνησης στο χωροχρόνο
Το κάθετο ευθύγραμμο τμήμα στην Εικόνα 1.3 (a) αντιστοιχεί σε ένα σημείο που μένει ακίνητο (σε σχέση με τους αστέρες) για κάποιο χρονικό διάστημα, από t1 έως t2. Δεδομένου οτι δεν διατρέχει κάποιο διάστημα στο χώρο, η χωρική συντεταγμένη-του είναι σταθερή, ίση με s0. Η Εικόνα 1.3 (b) δείχνει ένα σημείο που κινείται με αργή ταχύτητα, ώστε να διανύει ένα μικρό διάστημα χώρου μεταξύ s1 και s2, κατά τη διάρκεια ενός μεγαλύτερου διαστήματος χρόνου μεταξύ t1 και t2. Παρατηρήστε οτι αυτό που παραμένει σταθερό είναι το μήκος του ευθυγράμμου τμήματος . Στην Εικόνα 1.3 (c) βλέπουμε ένα σημείο που κινείται πολύ γρήγορα στο χώρο, πλησιάζοντας την ταχύτητα του φωτός (ένα πλασμοειδές πολύ μικρής μάζας, ας πούμε), ώστε τώρα το διάστημα με ιδιότητες χώρου s1s2 είναι μεγάλο, και το διάστημα με ιδιότητες χρόνου t1t2 είναι μικρό. Τέλος, η Εικόνα 1.3 (d) δείχνει ένα σημείο που κινείται ακριβώς με την ταχύτητα του φωτός (ένα πλασμοειδές μηδενικής μάζας), το οποίο διανύει ένα ορισμένο μήκος στο διάστημα s1s2, σε μηδέν χρόνο, δηλ. υπάρχει σε δυο διαφορετικές θέσεις στον ίδιο χρόνο (t0).
Η οικεία έννοια της ταχύτητας, στην παραπάνω αναλογία, αντιστοιχεί στη γωνία της γραμμής σε σχέση με τον χρονικό άξονα t. Επομένως στην Εικόνα 1.3 (a) η κλίση είναι μηδέν, και άρα η ταχύτητα του σημείου είναι μηδέν. Αλλά, αντιστοίχως, η δυϊκή έννοια της “χρονικής συνιστώσας του ρυθμού” αυτού του σημείου είναι η γωνία του ευθύγραμμου τμήματος σε σχέση με τον χωρικό άξονα s, και έτσι έχει τη μέγιστη τιμή-της. Στα διαγράμματα (b) και (c), η πρώτη γωνία (χωρική συνιστώσα, οικεία ταχύτητα) αυξάνεται, και η χρονική συνιστώσα (διπλή έννοια της ταχύτητας) μειώνεται· στο (d), τελικά μηδενίζεται. Η ταχύτητα του φωτός, c, αντιστοιχεί σε μια γωνία 90° σ’ αυτήν την αναλογία.
Το λάθος στην εικόνα 1.3 είναι οτι προσποιούμαστε πως ο χώρος είναι Ευκλείδειος (επίπεδος)· δηλ. οτι το μήκος του ευθύγραμμου τμήματος παραμένει αμετάβλητο καθώς το τμήμα περιστρέφεται στο επίπεδο. Αλλά ο χωροχρόνος σε έναν κόσμο ειδικής σχετικότητας δεν είναι Ευκλείδειος, αλλά “υπερβολικός” (ακολουθεί τη γεωμετρία του Minkowski), που σημαίνει οτι το μήκος του ευθύγραμμου τμήματος θα αλλάξει κάπως καθώς περιστρέφεται, εάν το μετρήσουμε με έναν από τους οικείους-μας χάρακες· αλλά αν το μετρήσουμε με έναν “υπερβολικό” χάρακα, κατάλληλο για γεωμετρία του Minkowski, τότε το μήκος θα προέκυπτε πάλι σταθερό, και το τετράγωνό του θα ήταν ίσο με s2 – t2. (Εναλλακτικά, μπορείτε να φανταστείτε οτι ο χώρος που απεικονίζεται δεν είναι επίπεδος, αλλά κυρτωμένος κατά κάποιον τρόπο.) Γιαυτό δεν μπορούμε να χρησιμοποιήσουμε την Εικόνα 1.3 για να κάνουμε ποσοτικές μετρήσεις: επειδή ο χώρος που φαίνεται εκεί δεν είναι σαν τον οικείο-μας Ευκλείδειο. Αλλά ποιοτικά, δηλ. σαν απλή αναλογία, η Εικόνα 1.3 είναι σωστή: μας δίνει έναν οπτικό τρόπο για να κατανοήσουμε αφενός τις έννοιες της οικείας ταχύτητας και της δυϊκής-της έννοιας (κατ’ αναλογία με τις γωνίες, με την ιδιότητα οτι η αύξηση της μιας προκαλεί την ελάττωση της άλλης), και αφετέρου την ιδέα οτι ανεξάρτητα από το πόσο γρήγορα κινείται ένα αντικείμενο στο χώρο, υπάρχει κάτι το αμετάβλητο σχετικά με αυτό: είναι το μήκος του ευθύγραμμου τμήματος, εάν αυτό μετρηθεί με έναν κατάλληλο χάρακα στη σωστή γεωμετρία.
1.6 Αν χρόνος = χώρος, πώς και δεν υπάρχει τύπος στη φυσική που να το δηλώνει αυτό;
Μα υπάρχει! Ορίστε, νά-τος:
s = c · t
Όλοι τον γνωρίζουν, αλλά λίγοι τον παίρνουν κατά κυριολεξία γι’ αυτό που πραγματικά λέει.
Ο παράγοντας c στον παραπάνω τύπο είναι μια σταθερά. Υπάρχει εκεί μόνο και μόνο επειδή χρησιμοποιούμε τις “επαρχιώτικες” μονάδες-μας για να μετρήσουμε χώρο και χρόνο· συγκεκριμένα το μέτρο (m) και το δευτερόλεπτο (s), οπότε λέμε οτι c = 299.792.458 m/s (μέτρα ανά δευτερόλεπτο). Αλλά η επιλογή-μας των μονάδων είναι αυθαίρετη. Θα μπορούσαμε εξίσου καλά να χρησιμοποιούμε το έτος-φωτός ως μονάδα του χώρου, και το έτος ως μονάδα του χρόνου, οπότε θα είχαμε c = 1 (έτος-φωτός ανά έτος), και τότε ο παραπάνω τύπος θα γραφόταν:
s = t
που λέει ακριβώς οτι χώρος και χρόνος είναι το ίδιο “υλικό”.
Ένας τρόπος για να εξαγάγουμε τον τύπο s = c·t είναι ο ακόλουθος. Ας υποθέσουμε οτι υπάρχουν δύο σημεία στο χώρο, s1 και s2. Ας υποθέσουμε ακόμα οτι κατά το χρόνο t1 ένα φωτόνιο ξεκινάει από το s1, κινείται προς την κατεύθυνση του s2, και φτάνει στο s2 κατά το χρόνο t2. Τότε τα γεγονότα (s1, t1) και (s2, t2) ονομάζονται ταυτόχρονα, και η σχέση που υπάρχει μεταξύ του χωρικού και του χρονικού διαστήματος είναι: (s2 – s1) = c · (t2 – t1)· ή, παραλείποντας τους δείκτες, μπορούμε να γράψουμε απλά: s = c·t. Το νόημα αυτού του τύπου είναι οτι κάθε ποσότητα χρόνου αντιστοιχεί σε μια ισοδύναμη ποσότητα χώρου. Για παράδειγμα, μας λέει οτι 1 δευτερόλεπτο χρόνου είναι ισοδύναμο με 299.792.458 μέτρα χώρου. Αν αντί για ένα φωτόνιο χρησιμοποιήσουμε στην ανωτέρω περιγραφή ένα υλικό σωματίδιο που κινείται με ταχύτητα v, τότε παίρνουμε τον τύπο s = v·t, γνωστό από τη φυσική του γυμνασίου.
2. Η μαγική πράξη (με την οποία εξαφανίζεστε)
Αν ο χρόνος είναι πραγματικά σαν τον χώρο, όπως προτάθηκε στην §1, και αν ο τρόπος που ο χρόνος και ο χώρος γίνονται αντιληπτοί εξαρτάται από τη φυσική σύσταση του αντιλαμβανόμενου όντος (ήτοι αν αποτελείται κυρίως από μάζα τότε ο χρόνος ρέει και ο χώρος είναι· ενώ αν αποτελείται κυρίως από ενέργεια τότε ο χώρος ρέει και ο χρόνος είναι), τότε η εικόνα του σύμπαντος που προκύπτει είναι η εικόνα ενός “παγωμένου” κόσμου, τον οποίο μερικοί επιστήμονες αποκαλούν “κόσμο–μονόλιθο” (“block world” π.χ.: Dickson[3] σ. 165–174). Σε ένα τέτοιο κόσμο, κάθε γεγονός που συνέβη ή που πρόκειται να συμβεί υπάρχει ήδη εκεί, κείται στο τετραδιάστατο χωροχρονικό συνεχές.
Ας το επαναλάβουμε αυτό, απεικονίζοντάς το σε ένα σχέδιο, επειδή παίζει κεντρικό ρόλο στο κόλπο της εξαφάνισής σας. Κοιτάξτε το επόμενο διάγραμμα, που είναι επανάληψη ενός τμήματος της Εικ. 1.3:
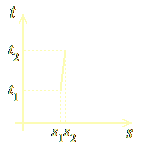
Εικόνα 2.1. Ο χωροχρόνος σαν κόσμος–μονόλιθος: πρόκειται για σημείο που κινείται, ή για μια ακίνητη γραμμή;
Τί δείχνει η Εικ. 2.1; Από μια οπτική γωνία, δείχνει ένα σημείο που κινείται από τη θέση s1 στη θέση s2, πραγματοποιώντας-το αυτό μεταξύ των αντίστοιχων χρόνων t1 και t2. Αλλά από μια άλλη οπτική γωνία, δεν δείχνει την παραμικρή κίνηση· δείχνει απλώς μια γραμμή που είναι εκεί, μην κάνοντας απολύτως τίποτα· μια “παγωμένη” γραμμή. Και, όπως αυτό μπορούμε να το φανταστούμε για σημεία με ομαλή κίνηση, μπορούμε επίσης να το φανταστούμε για οποιοδήποτε τριδιάστατο αντικείμενο, συμπεριλαμβανομένου και του εαυτού-σας (και του εαυτού-μου, και οποιουδήποτε άλλου). Αντί για πολυάσχολα πλάσματα που μετακινούμαστε στο χώρο, μπορούμε να φανταστούμε τους εαυτούς-μας σαν παγωμένα αντικείμενα στον τετραδιάστατο χωροχρόνο. Στην πραγματικότητα δεν δρούμε, δεν κινούμαστε, δεν κάνουμε τίποτα στις 4 διαστάσεις, απλά είμαστε, σύμφωνα με αυτή την εναλλακτική οπτική.
Κάτι όμως δεν πάει καλά. Εάν ο χρόνος είναι ακριβώς σαν το χώρο, αν ο κόσμος-μας έχει τέσσερις πανομοιότυπες διαστάσεις, γιατί συμβαίνει να υπάρχει διάκριση μεταξύ αυτής της διάστασης (χρόνος) και των τριών άλλων (χώρος); Αυτή η διαφορά πρέπει να είναι αντικειμενική, ανεξάρτητη της ανθρώπινης νόησης, και ιδού γιατί: ας φανταστούμε έναν παρατηρητή που έρχεται “έξω” από το σύμπαν-μας (ας αγνοήσουμε για λίγο το οτι δεν γνωρίζουμε αν ένα τέτοιο “έξω” υφίσταται) και ρίχνει μια ματιά στο σύμπαν-μας από μακριά (ας αγνοήσουμε επίσης της νοητικές ικανότητες που αυτός ο παρατηρητής θα πρέπει να έχει). Ο παρατηρητής λοιπόν “αντιλαμβάνεται” τον κόσμο-μας, και λέει: «Αχά! Υπάρχουν εδώ κάποια τετραδιάστατα όντα που διαθέτουν κυρίως μάζα, και οι τριδιάστατες προβολές-τους νομίζουν οτι αυτή η διάσταση ρέει, ενώ οι άλλες τρεις απλά υπάρχουν εκεί γύρω-τους.» Γιατί είναι σε θέση ο εξω-κοσμικός παρατηρητής να διακρίνει μια από τις τέσσερις διαστάσεις (το χρόνο) και να την επισημάνει ως ξεχωριστή;
Η απάντηση είναι οτι υπάρχει μια αντικειμενική διαφορά μεταξύ χρόνου και χώρου. Αλλά δεν πρόκειται να επεκταθώ σε αυτό το θέμα τώρα επειδή είναι άσχετο με τους σκοπούς του κόλπου της εξαφάνισης. Η διαφορά θα παρουσίαζε ενδιαφέρον για τον φιλόσοφο, αν θα τον ενδιέφερε ποτέ κάποια ιδέα που δεν προήλθε από τη διάνοιά του. Σε κάθε περίπτωση, η διαφορά περιγράφεται στην πρώτη αντίρρηση στην ενότητα των Σχολίων Αναγνωστών (§4), και εξηγεί γιατί βρίσκουμε τους εαυτούς-μας σε αυτή τη μεριά του φάσματος ενέργειας-μάζας (δηλ. διαθέτοντας πολλή μάζα και σχεδόν καθόλου κινητική ενέργεια), γιατί δεν μπορούμε να είμαστε στην άλλη μεριά (μικρή μάζα, πολλή ενέργεια), και γιατί η γεωμετρία του κόσμου-μας θα πρέπει να είναι σχετικιστική, όχι Ευκλείδεια. Αλλά, καθώς είπα, ποιος νοιάζεται για όλα αυτά. Εμάς μας ενδιαφέρει το κόλπο της εξαφάνισης. Είσαστε έτοιμοι;
Ας υποθέσουμε για λίγο οτι η εναλλακτική άποψη είναι η “σωστή”, δηλαδή ο χρόνος είναι ακόμα μια χωρική διάσταση, εξαιρετικά παρόμοια με τις άλλες τρείς (αν και μπορεί να διακριθεί γεωμετρικά), και μόνο η νόησή μας ευθύνεται για την “πολυπλοκοποίηση” της όλης εικόνας, κάνοντας τον χρόνο να φαίνεται τόσο διαφορετικός. Στην πραγματικότητα, τίποτα δεν κινείται, τίποτα δεν αλλάζει, όλα είναι παγωμένα. Έτσι, θα μπορούσαμε ακόμα και να αντιστρέψουμε το γνωστό ρητό του αρχαίου Ηράκλειτου:(13)
| Τὰ πάντα μένει, καὶ οὐθὲν ῥεῖ. |
Τώρα αν τίποτα δεν ρέει, τί συμβαίνει με τις δικές-μας σκέψεις; Πρέπει να είναι κι αυτές παγωμένες, σωστά;
“Παγωμένες σκέψεις” σημαίνει νοητικά μοτίβα που υπάρχουν ταυτόχρονα πριν και μετά το “τώρα” (το οποίο είναι μια απλή ψευδαίσθηση του τριδιάστατου εαυτού-μας). Ας σκεφτούμε την αναλογία τέτοιων σκέψεων με την “παγωμένη μουσική” στα αυλάκια ενός παλιομοδίτικου δίσκου LP (ή ακόμα και σε ένα σύγχρονο CD, μόνο που τα αυλάκια σε ένα CD δεν μπορούν να διακριθούν με το γυμνό μάτι). Η μουσική ακούγεται σαν μουσική όσο μια συσκευή ανάγνωσης (π.χ. μια βελόνα, μια ακτίνα λέιζερ) κινείται κατά μήκος τον αυλακιών. Αλλά εάν δεν υπάρχει μια τέτοια πράξη ανάγνωσης, αν το μόνο που έχουμε είναι το σύνολο των αυλακιών στο δίσκο, τότε αυτό δεν μας δίνει την αίσθηση της μουσικής, σωστά; Κατά παρόμοιο τρόπο, εάν ο χρόνος είναι παγωμένος, οι σκέψεις-μας δεν μοιάζουν και πολύ σαν σκέψεις πλέον. Γιατί, στο κάτω-κάτω, οι μελλοντικές-μας σκέψεις είναι ήδη σχεδιασμένες. Το “τώρα-μας” (ο τριδιάστατος εαυτός-μας) δεν γνωρίζει τις μελλοντικές-μας σκέψεις, οπότε αυτές εμφανίζονται σαν να μην τις έχουμε κάνει ακόμα. Αλλά στην πραγματικότητα — στην παγωμένη πραγματικότητα — ο τετραδιάστατος εαυτός-μας τις έχει όλες εντός-του. Κατά συνέπεια, εμείς (οι πλήρεις, τετραδιάστατοι εμείς) δεν σκεφτόμαστε. Νομίζουμε οτι σκεφτόμαστε, αλλά πλανώμαστε. Η πλάνη-μας προέρχεται από το οτι έχουμε την αντίληψη μιας τριδιάστατης “προβολής” του τετραδιάστατου εαυτού-μας ανά πάσα στιγμή, και τη διατήρηση στην μνήμη-μας μερικών παραστάσεων προηγούμενων προβολών του εαυτού-μας. Αλλά στον τετραδιάστατο εαυτό-μας δεν υπάρχουν τέτοιου είδους χρονικές προβολές, παρά μόνο εμείς σαν ένα συνεχόμενο, μακρύ, τετραδιάστατο “τεμάχιο”, από τη γέννηση ως το θάνατο. Και αυτό το “τεμάχιο” δεν σκέφτεται καμία σκέψη, ακριβώς όπως ένα LP ή CD που το βλέπουμε στην ολότητά του δεν παίζει καμία μουσική.
Αλλά εάν ο τετραδιάστατος εαυτός-μας δεν σκέφτεται, έπεται οτι…
| Η ίδια η νόηση είναι μια ψευδαίσθηση. |
Τί νόημα, τότε, έχει το να πούμε οτι “υπάρχουμε”; Η ύπαρξη μπορεί να γίνει αντιληπτή μόνο μέσα στο ρέοντα χρόνο: κάτι μπορεί να είναι τώρα εδώ, και συνεχίζει να βρίσκεται εδώ (ή εκεί) λίγο αργότερα, οπότε και λέμε οτι συνεχίζει να υπάρχει μεταξύ αυτών των δύο χρόνων. Εάν ο χρόνος δεν ρέει, εάν έχει την ποιότητα του χώρου, τότε τί νόημα έχει να πούμε για οτιδήποτε οτι “υπάρχει”; Επίσης, ας σημειώσουμε τη φράση: «Η ύπαρξη μπορεί να γίνει αντιληπτή…», παραπάνω· εάν η νόηση είναι μία ψευδαίσθηση, πώς μπορεί κάτι να γίνει “αντιληπτό”;
| Πόρισμα: Δεν υπάρχουμε. |
Έτσι ολοκληρώνεται το κόλπο της εξαφάνισης. Αλλά ας κάνουμε μερικές ακόμα σκέψεις.
Αν οι σκέψεις-μας, συμπεριλαμβανομένων και των μελλοντικών, κείνται όλες στο τετραδιάστατο χωροχρονικό συνεχές, τότε στην πραγματικότητα δεν αποφασίζουμε τίποτα με τη δική-μας ελεύθερη βούληση. Μας δίνεται η ψευδαίσθηση οτι αποφασίζουμε, γιατί το “τώρα-μας” είναι απληροφόρητο σχετικά με τα μελλοντικά-μας “τώρα”. Αλλά τί σημασία έχει τί ξέρει ή αγνοεί το “τώρα-μας”; Οι μελλοντικές αποφάσεις-μας είναι προαποφασισμένες, οπότε...
| Και η ελεύθερη βούληση είναι μια αυταπάτη. |
«Α!... Μισό λεπτό!» σας ακούω να λέτε. «Ακόμα κι αν είναι αλήθεια όλα αυτά τα μαύρα μαντάτα, υπάρχει ένας βράχος που παραμένει ακλόνητος, αμόλυντος από τη χυδαία επίθεσή σου στην ανθρώπινη φύση: είναι ο Θεός! Ο Θεός στέκει έξω απ’ όλον αυτόν το νεκρό τετραδιάστατο (ή ν-διάστατο) κόσμο. Ο Θεός είναι αυτός που μπορεί να μας παρατηρεί και να γνωρίζει τις μελλοντικές καταστάσεις-μας, γιατί, αντίθετα από μας, ο Θεός δεν βλέπει μόνο τριδιάστατες “προβολές”, αλλά ολόκληρους τους τετραδιάστατους εαυτούς-μας: παρελθόντες, παρόντες, και μέλλοντες!»
Σιγά παρακαλώ, πατήστε λίγο φρένο. Φοβάμαι οτι τα νέα δεν είναι και τόσο καλά, ούτε για το Θεό-σας. Είπατε: «Ο Θεός παρατηρεί»; Ε, όχι με κάποιο ζευγάρι μάτια ελπίζω, σωστά; Ο Θεός γνωρίζει τα πράγματα, αυτό δεν εννοείτε; (Ο Θεός δεν είναι εκείνος ο Πάνσοφος τύπος;) Αλλά αν ο Θεός γνωρίζει οτιδήποτε, τότε πρέπει να είναι ένα νοήμον Ον, να έχει νόηση. Δεν είναι δυνατόν να ισχυρίζεστε οτι ο Θεός είναι Πάνσοφος, οτι αντιλαμβάνεται και θυμάται καταστάσεις (και ακόμη ακούει προσευχές και κάνει κρίσεις, όπως πιστεύουν πολλοί άνθρωποι), και να επιμένετε οτι ο Θεός δεν είναι νοήμον Ον! Αλλά αν ο Θεός είναι νοήμον Ον, τότε...
| Ούτε ο Θεός υπάρχει. |
Φυσικά, θα πρόσθετα εγώ, καθώς πιστεύω οτι ο Θεός είναι δημιούργημα της ανθρώπινης διανόησης· και σαν τέτοιο, πάσχει από τα ίδια ελαττώματα που μαστίζουν την ανθρώπινη διανόηση στην ολότητά της. Αλλά, πραγματικά, δεν έχει καμιά σημασία το τί πιστεύω εγώ για τον Θεό, γιατί το παραπάνω πόρισμα είναι ανεξάρτητο της προσωπικής-μου άποψης. Απλώς λέει οτι αν ο Θεός γνωρίζει οτιδήποτε, τότε, εξ αιτίας του οτι είναι νοήμων, δεν μπορεί να υπάρχει, αφού κανένα νοήμον ον δεν υπάρχει («η νόηση είναι μια ψευδαίσθηση», βλ. παραπάνω). Αλλιώς, αν επιμένετε οτι ο Θεός-σας υπάρχει, τότε πρέπει να παραδεχτείτε οτι ο Θεός-σας δεν είναι νοήμων, δηλαδή δεν γνωρίζει τίποτα. (Επαναλαμβάνω την ίδια ιδέα με διάφορους τρόπους γιατί γνωρίζω πολύ καλά την ανικανότητα — ή απροθυμία — των πιστών ανθρώπων να χρησιμοποιήσουν και να εφαρμόσουν την κοινή λογική όταν πρόκειται για θέματα της πίστης-τους.)
2.1 Ανέφικτο το ταξίδι στο χρόνο πίσω στο παρελθόν.
Ας βγάλουμε ένα τελευταίο λογικό συμπέρασμα από τα παραπάνω. Υπάρχει ένα αγαπημένο και διαρκώς επαναλαμβανόμενο μοτίβο στην επιστημονική φαντασία: το ταξίδι στο χρόνο. Από την εποχή του βιβλίου Η μηχανή του χρόνου (1895) του Χ. Τζ. Γουελς, οι άνθρωποι συνεχίζουν να διαβάζουν για άλλους, φανταστικούς ανθρώπους, οι οποίοι ταξιδεύουν πίσω και εμπρός στο χρόνο. Και δεν είναι μόνο η επιστημονική φαντασία· ενίοτε είναι και η καθαυτό επιστήμη (ή τουλάχιστον αυτή που θεωρείται τέτοια). Σε μια ειδική έκδοση του Scientific American αφιερωμένη στο ζήτημα του χρόνου, ένα άρθρο εξέτασε στα σοβαρά την πιθανότητα ενός ταξιδιού στο χρόνο, και δεν ήταν το μόνο άρθρο περί της ιδέας αυτής στο συγκεκριμένο περιοδικό. Αλλά αν τα πάντα μένουν και τίποτα δεν ρέει, με ποια έννοια είναι το ταξίδι στο χρόνο εφικτό;
Οφείλω να επισημάνω αμέσως οτι υπάρχει κάποια λογική σύμφωνα με την οποία το ταξίδι στο χρόνο προς το μέλλον είναι δυνατό, και με περισσότερους από έναν τρόπους. Για παράδειγμα, ίσως μπορεί κάποιος να εισέλθει σε κατάσταση βαθιάς ψύξης, και να ξεπαγώσει με ανώτερη τεχνολογία στο μέλλον, όπως επιδιώκεται στον τομέα της κρυονικής. Εναλλακτικά, μπορεί κανείς να ταξιδέψει αρκούντως μακριά και με αρκούντως μεγάλη ταχύτητα, οπότε κατά την επιστροφή να ανακαλύψει οτι έχει περάσει πολύ περισσότερος χρόνος στον τόπο αναχώρησης και άφιξης απ’ ότι στο ρολόι-του και στους βιολογικούς ρυθμούς γήρανσής του, όπως προβλέπει η θεωρία της σχετικότητας. Καμία από αυτές τις μεθόδους ταξιδιού στο μέλλον δεν έρχεται σε αντίφαση με τις ιδέες που συζητήθηκαν μέχρι στιγμής. Από μια οπτική τεσσάρων διαστάσεων, ένα τριδιάστατο ον που πραγματοποιεί αυτού του είδους το ταξίδι στο χρόνο είναι απλά ένα ον με ένα τμήμα της ύπαρξης του να εμφανίζεται ομοιόμορφο κατά τη φορά του χρόνου (βλ. επόμενο διάγραμμα).

Εικόνα 2.2. Δύο τρόποι να παραταθεί μια συνηθισμένη ύπαρξη (άνω): το “κρυονικό όνειρο” (μέσον) και το “σχετικιστικό όνειρο” (κάτω)
Τα παραπάνω διαγράμματα δείχνουν δύο δυνατότητες για κάτι που θα μπορούσε να θεωρηθεί σαν “ταξίδι στο χρόνο προς το μέλλον”. Τα σχέδια είναι αφηρημένα. Αυτό στην κορυφή δείχνει μια συνηθισμένη ζωή, με “τα πάνω και τα κάτω-της”, με το χρόνο να ρέει από αριστερά προς τα δεξιά. Στο μεσαίο διάγραμμα η ζωή εισέρχεται σε μια παγωμένη κατάσταση σε δοσμένο χρόνο, κατά την οποία τίποτα δεν συμβαίνει, και αργότερα “αποψύχεται” και συνεχίζει κανονικά. Το κατώτερο διάγραμμα δείχνει μια ζωή που προχωρά φυσιολογικά μέχρι ένα ορισμένο χρόνο, οπότε και επιβιβάζεται σε ένα ταχέως κινούμενο διαστημόπλοιο, ταξιδεύει αρκετά μακριά στο χώρο, και επιστρέφει στο σημείο αναχώρησής της, επιβραδύνοντας έτσι ουσιαστικά τους βιολογικούς-της ρυθμούς.
Δεν υπάρχει τίποτα το αδύνατο στις περιπτώσεις που μόλις περιγράφηκαν (αν και υπάρχουν πολλά απίθανα πράγματα, τουλάχιστον με τις σημερινές τεχνολογικές προδιαγραφές). Στην ουσία, τα παραπάνω διαγράμματα μπορεί να θεωρηθεί οτι δείχνουν τα όντα στην ολότητά τους, δηλ. αναπτυγμένα στο χρόνο. Η μόνη παρατήρηση που αξίζει να κάνουμε τότε είναι οτι κάποια απ’ τα ανωτέρω όντα έχουν ένα κομμάτι της ύπαρξής τους που είναι ουσιαστικά διαφορετικό από την υπόλοιπη ύπαρξή τους· εάν το ακολουθήσουμε κατά μήκος της χρονικής διάστασης (προς οποιαδήποτε κατεύθυνση!) βλέπουμε οτι εμφανίζεται σχετικά ομοιόμορφο — και αυτό είναι όλο.
Αλλά το ταξίδι στο χρόνο στην επιστήμη (και στην επιστ. φαντασία) συνήθως δεν περιλαμβάνει κανένα από τα παραπάνω είδη, αλλά ένα άλλο, κατά το οποίο ο ταξιδιώτης επιστρέφει στο παρελθόν, και μάλιστα μπορεί ακόμα και να συναντήσει τον δικό-του πρότερο εαυτό. Σύμφωνα με τα παραπάνω, αυτό είναι λογικά αδύνατον. Ένας “ταξιδιώτης” είναι ένα 3-διάστατο χρονικό στιγμιότυπο μιας ολότητας (4-διάστατης ύπαρξης) ενός όντος. Όμως ένα 3-διάστατο στιγμιότυπο δεν ταξιδεύει, απλά είναι· βρίσκεται απλώς δίπλα σε άλλα στιγμιότυπα κατά μήκος της χρονικής διάστασης. Πώς μπορεί ένα 3-διάστατο στιγμιότυπο ενός όντος να μετακινηθεί οπουδήποτε στο χρόνο σε μια στατική εικόνα; Καμία κίνηση 3-διάστατων στιγμιοτύπων δεν είναι εφικτή. Μπορεί κανείς μόνο να παρατηρεί διαφορετικά 3-διάστατα στιγμιότυπα, που όλα βρίσκονται εκεί, στον 4-διάστατο χωροχρόνο. Τίποτα δεν κινείται, τίποτα δεν ταξιδεύει στο χρόνο. Υπάρχει μόνο μια — ελαφρώς άσχετη — δυνατότητα: ένα από αυτά τα 3-διάστατα στιγμιότυπα του όντος να αποκτήσει στη μνήμη-του την αντίληψη ενός κόσμου στον οποίο εμφανίζεται σε 3-διάστατο στιγμιότυπο του παρελθόντος-του, σε ένα είδος εικονικής πραγματικότητας. Αλλά κάτι τέτοιο συνήθως δεν είναι αυτό που φαντάζονται οι συγγραφείς επιστημονικής φαντασίας. Επομένως:
| Το πραγματικό ταξίδι στο χρόνο προς το παρελθόν είναι ένας παραλογισμός. |
2.2 Γιατί , στο κάτω-κάτω, να θεωρήσει κανείς στα σοβαρά την ιδέα “Χρόνος = Χώρος”;
Ένας φίλος-μου, αφού υπέστη το παραπάνω κόλπο της εξαφάνισης, αρνήθηκε να εξαφανιστεί για τους παρακάτω λόγους:
«Γιατί θα πρέπει να αποδεχτώ τη θέση οτι ο χρόνος και ο χώρος είναι πραγματικά ένα και το αυτό;» ρώτησε ο φίλος-μου. «Θα μπορούσα κάλλιστα και εγώ να φανταστώ οτι ο χρόνος είναι ακριβώς όπως τον αντιλαμβάνομαι: μια αλληλοδιαδοχή από “τώρα”, και η ύπαρξή μου περνάει διαμέσου αυτών των “τώρα”, αφήνοντας πίσω αυτά που έχω ήδη βιώσει, γνωρίζοντας οτι θα συναντήσω μπροστά-μου αυτά που δεν έχω ακόμα βιώσει. Ποιο είναι το πρόβλημα με αυτή την άποψη;»
Υπάρχει κάτι εγγενώς λανθασμένο σ’ αυτή την άποψη, το οποίο πρόκειται να συζητήσω στην 3η ένσταση της ενότητας Απόψεις Αναγνωστών (§4). Αλλά σε αυτό το σημείο θα ήθελα να προσποιηθώ για μια στιγμή οτι δεν υπάρχει κανένα εγγενές λάθος σ’ αυτήν, επειδή ακόμα και τότε μπορούμε να κάνουμε μερικές ενδιαφέρουσες παρατηρήσεις.
Λοιπόν, γιά να δούμε: παρομοίως, δεν υπάρχει κανένα εγγενές λάθος με το γεωκεντρικό μοντέλο, ή με την αντίληψη των χρωμάτων, ή με το να νομίζουμε οτι οι τροχιές των πλανητών είναι πράγματι ελλείψεις (ή άλλες κωνικές τομές). Σίγουρα, για κάθε μια από αυτές τις απόψεις μπορεί να υποστηριχτεί το επιχείρημα της ανάγκης διατήρησης της άποψης αυτής μαζί με την εναλλακτική-της. Δεν υφίσταται εκ των προτέρων κάποια λογική αιτία για να δικαιολογηθεί το γιατί οι πιο πολύπλοκες απόψεις πρέπει να εγκαταλειφθούν για χάρη των απλούστερων. Πράγματι, στην πράξη κάποτε διατηρούμε μερικές από αυτές τις θέσεις. Λόγου χάρη, παρόλο που γνωρίζουμε οτι δεν υπάρχουν χρώματα στον κόσμο, παρά μόνο μήκη κύματος, συνεχίζουμε να έχουμε τη Θεωρία των Χρωμάτων στην οπτική, επειδή μέσω αυτής μπορούμε να κατασκευάσουμε αντικείμενα που είναι χρήσιμα (π.χ., ένα προβολέα που χρησιμοποιεί τα τρία βασικά χρώματα, κόκκινο – πράσινο – μπλε, για να δημιουργήσει μια έγχρωμη εικόνα σε μια οθόνη προβολής). Και παρόλο που οι ελλείψεις σε τριδιάστατο χώρο είναι στην πραγματικότητα ευθείες γραμμές σε τετραδιάστατο χώρο, οι υπολογισμοί που επιτρέπουν στα διαστημόπλοια να ταξιδεύουν γύρω από τους πλανήτες εξακολουθούν να εμπεριέχουν ελλείψεις, τρεις διαστάσεις, και το χρόνο σαν μια ξεχωριστεί διάσταση, αντί ευθείες γραμμές και τέσσερις διαστάσεις, γιατί η πρώτη επιλογή είναι αυτή που μπορούμε εύκολα να κατανοήσουμε.
Έτσι, συνήθως χρησιμοποιούμε στη φυσική το μοντέλο που μας είναι χρήσιμο, κι όχι αυτό που είναι πιο οικονομικό, απλούστερο, πιο σαφές και σύντομο. Αυτό το κάνουμε επειδή μας περιορίζει η ανθρώπινη ιδιοσυγκρασία, οπότε πρέπει να δουλεύουμε με όρους που κατανοούμε (χρώμα, έλλειψη, κλπ). Αυτή είναι η πρακτική όψη της φυσικής: μας βοηθάει να χτίσουμε συσκευές, να κατασκευάσουμε πράγματα που κάνουν τη ζωή-μας ευκολότερη. Όμως μια άλλη πτυχή της φυσικής είναι οτι, μέσω αυτής, οι επιστήμονες προσπαθούν να φτάσουν στη βαθύτερη ουσία των πραγμάτων στον κόσμο. Μόνο με το να προσπαθούν, επί 2.500 χρόνια, να κατανοήσουν τη βαθύτερη ουσία της φύσης, κατάφεραν οι άνθρωποι να γενικεύσουν, να ενοποιήσουν, να απλοποιήσουν θεωρίες, και τελικά να αποκτήσουν την απαραίτητη γνώση μέσα από τέτοιες “μεγάλες απλουστεύσεις”, και να χτίσουν χρήσιμες (και μερικές φορές φονικές) μηχανές. Για παράδειγμα, η πυρηνική ενέργεια (η οποία μας έδωσε μια εναλλακτική πηγή ενέργειας εκτός των υδρογονανθράκων, αλλά και — αλλίμονο! — μια Χιροσίμα και ένα Ναγκασάκι), έγινε δυνατή μόνο αφότου οι επιστήμονες έκαναν την μεγάλη ενοποίηση του ηλεκτρισμού και του μαγνητισμού· που επέτρεψε στον Τζέιμς Κλερκ Μάξγουελ να καταλήξει στην εξίσωση για τα ηλεκτρομαγνητικά πεδία· η οποία επέτρεψε στους φυσικούς να αποκτήσουν μια καλύτερη κατανόηση του φωτός και των ιδιοτήτων-του· που επέτρεψε στον Αϊνστάιν να συλλάβει πρώτα την ειδική, και έπειτα τη γενική θεωρία της σχετικότητας· η οποία ήταν απαραίτητη για το χτίσιμο των συσκευών που χρησιμοποίησαν την πυρηνική ενέργεια, με τη μετατροπή της μάζας σε ενέργεια. Ακόμα και η ταπεινή απλοποίηση οτι το φώς είναι απλώς μήκη κύματος (και ως εκ τούτου οτι τα χρώματα είναι μόνο μια παρωχημένη ανθρώπινη προσθήκη στον κόσμο), ήταν απαραίτητη για πολλές τεχνολογικές καινοτομίες κατά τον 20ό αιώνα. Εάν δεν είχαμε μια βαθύτερη, γενικευμένη γνώση της φυσικής, καμία από τις συσκευές που μας περιτριγυρίζουν τώρα — συμπεριλαμβανομένου και του διαδικτύου και του υπολογιστή στον οποίο διαβάζετε το παρόν — δεν θα ήταν δυνατή. Θα ζούσαμε ακόμα σε σπίτια φωτιζόμενα με κεριά — ή ίσως σε καλύβες και παράγκες — ξυπνώντας και κοιμώμενοι με τους ρυθμούς των ζώων-μας.
Έτσι, οι φυσικοί διατηρούν της σύνθετες θεωρίες εφόσον αυτές αποδεικνύονται χρήσιμες· αλλά επίσης δουλεύουν με τις γενικευμένες/ ενοποιημένες/απλοποιημένες για δύο διαφορετικούς λόγους: (1) για να κάνουν περαιτέρω προόδους στο μέλλον, εκμεταλλευόμενοι την βαθύτερη κατανόηση που αυτές παρέχουν, και (2) επειδή οι φυσικοί έχουν περιέργεια, και θέλουν να γνωρίζουν πώς είναι ο κόσμος πραγματικά. Τί σημαίνει το «πώς είναι ο κόσμος πραγματικά»; Λοιπόν, εάν παραδεχτούμε οτι τα ανθρώπινα όντα είναι ένα ασήμαντο είδος, που ζει σε μια μικροσκοπική κουκκίδα ύλης, που περιστρέφεται γύρω από ένα συνηθισμένο κίτρινο άστρο, που στροβιλίζεται μαζί με εκατοντάδες δισεκατομμύρια άλλα αστέρια σε ένα μη ξεχωριστό γαλαξία, έναν από τους εκατοντάδες δισεκατομμύρια γαλαξίες μέσα σε αυτό που αποκαλούμε “σύμπαν” (το οποίο μπορεί να είναι απλώς ένα μεταξύ ενός ανείπωτου αριθμού άλλων συμπάντων), τότε συνειδητοποιούμε οτι η έννοια “χρώμα” δεν είναι κάτι που πραγματικά θα πρέπει να αφορά τη φυσική. Μπορεί να αφορά τη φυσική του ανθρώπου, το είδος της φυσικής που οδηγεί σε εφαρμογές χρήσιμες για εμάς, αλλά δεν θα πρέπει να αφορά την βαθύτερη, ανεξάρτητη του ανθρώπου κατανόηση του κόσμου. Με παρόμοιο τρόπο, παίρνοντας το χρόνο ως κάτι το ιδιαίτερο, ξεχωριστά από το χώρο — που είναι η προσέγγιση στην φυσική του ανθρώπου — έχουμε όλες τις χρήσιμες εφαρμογές σήμερα, αλλά αυτή είναι μια ανθρωποκεντρική οπτική, επειδή είναι η νόησή μας που κάνει το χρόνο να εμφανίζεται σαν κάτι το ιδιαίτερο. Μια φυσική ανεξάρτητη του ανθρώπου πρέπει να ασχολείται με τον τετραδιάστατο χωροχρόνο, τουλάχιστον στο μακρόκοσμο. Και εκείνοι οι φυσικοί — ή και οι υπόλοιποι — που θέλουν να ξέρουν «πώς είναι πραγματικά» ο κόσμος, πρέπει να έχουν κατά νου την ενοποίηση του χώρου και του χρόνου (και ως εκ τούτου την αυταπάτη της ροής του χρόνου).
Αλλά όπως είπα, πέρα απ’ όλα τα παραπάνω,
υπάρχει κάτι το εγγενώς λανθασμένο με τη σκέψη του φίλου-μου. Μπορείτε να δείτε
πού είναι το λάθος στην 3η
ένσταση της ενότητας Απόψεις Αναγνωστών
(§4), αλλά εάν πηδήσετε και πάτε εκεί κατευθείαν θα χάσετε όλα τα ωραία στο
ενδιάμεσο. ![]() Έχετε υπομονή!
Έχετε υπομονή!
2.3 Και τί γίνεται με την εξαφάνιση των πάντων;
Πάνω σ’ αυτό, έχω μια πρόταση να κάνω. Δεν μας βοηθάει πραγματικά με κανένα τρόπο να φιλοσοφούμε και να συμπεραίνουμε οτι δεν υπάρχουμε. Μπορεί να ισχύει οτι η χωρο-χρονική ενοποίηση μας λέει πως η νόησή μας είναι περιορισμένη, κι οτι είμαστε εντελώς ασήμαντοι στον ευρύτερο κοσμικό καμβά. Αλλά τότε… ε, και λοιπόν; Ήδη το γνωρίζαμε αυτό. Απλά, πολλοί άνθρωποι αρνούνται να το παραδεχτούν — άλλωστε η ματαιοδοξία είναι μέρος της ανθρώπινης φύσης. Αλλά ολόκληρη η ιστορία της επιστήμης είναι μια ιστορία του πώς οι άνθρωποι έμαθαν οτι δεν είναι ξεχωριστοί, αντίθετα με τα φαινόμενα που απατούν. Πρώτα έμαθαν οτι η Γη δεν βρίσκεται στο κέντρο του κόσμου· στη συνέχεια οτι τα ανθρώπινα όντα δεν είναι κάτι το ιδιαίτερο, αλλά απλώς ένα ακόμα ζωικό είδος, και οτι δεν δημιουργήθηκαν με κάποιον ιδιαίτερο τρόπο, αλλά προέκυψαν μέσω της βιολογικής εξέλιξης, όπως ακριβώς κάθε άλλο έμβιο ον· μετά έμαθαν οτι δεν υπάρχει πουθενά κέντρο του σύμπαντος, και πως η τοποθεσία-μας είναι εξίσου τετριμμένη και κοινή με κάθε άλλη τοποθεσία στον τριδιάστατο χώρο. Αλλά στον 20ό αιώνα προέκυψαν κάποιες ιδέες, κυρίως μεταξύ κβαντικών φυσικών, που πρότειναν οτι η ανθρώπινη νόηση είναι πράγματι κάτι το ιδιαίτερο. Ένας τέτοιος φυσικός, ο γεννημένος στη Βρετανία Αμερικανός Freeman Dyson (Φρήμαν Ντάισον), είπε μάλιστα οτι, κατά κάποιον τρόπο, «το σύμπαν γνώριζε οτι ερχόμαστε». Η ενοποίηση του χωροχρόνου θα μας βοηθήσει να ξανάρθουμε στα συγκαλά-μας, συνειδητοποιώντας την ανοησία αυτής της δήλωσης. Νομίζω οτι η χωρο-χρονική ενοποίηση είναι ένα καλό χαστούκι στα αλαζονικά πρόσωπά μας, επιτρέποντάς μας να ξυπνήσουμε και να σκεφτούμε ταπεινά και πάλι. Σε μερικούς μπορεί να μην αρέσει αυτό, αλλά το σύμπαν δεν θα μπορούσε να νοιάζεται λιγότερο.
2.4 Αλλά τί γίνεται με την ελεύθερη βούληση;
Αυτό αποτελεί πρόβλημα μόνο αν πιστεύετε οτι υπάρχει ένα ον-παντογνώστης που ξέρει το μέλλον-μας (ή απλά μπορεί να το μάθει, ακόμα κι αν το ον δεν επιθυμεί κάτι τέτοιο, από διακριτικότητα). Ήτοι, αυτό είναι πρόβλημα για ορισμένους θρήσκους ανθρώπους. Για εμένα δεν είναι, επειδή δεν πιστεύω οτι υπάρχει κάποιος που γνωρίζει τις μελλοντικές-μου αποφάσεις και πράξεις. Εάν το κομμάτι “τώρα” του εαυτού-μου είναι τόσο ανίδεο για το μέλλον-μου όσο γνωρίζω (και εσείς συμφωνείτε) οτι είναι, τότε δεν έχει καμία διαφορά εάν οι πράξεις και οι αποφάσεις ενός 4D όντος είναι προκαθορισμένες ή όχι, αφού κανένας δεν τις γνωρίζει. Εάν πιστεύετε οτι κάποιος (ο Θεός;) τις γνωρίζει, τότε συμφωνώ, αντιμετωπίζετε ένα φιλοσοφικό αίνιγμα. Διαβάστε περαιτέρω επιχειρηματολογία επί του θέματος αυτού σε αυτή τη σελίδα-μου.
3. Σχετικές σκέψεις και συναφείς εργασίες
Καμία από τις παραπάνω ιδέες δεν είναι αυθεντικά καινούργια· δηλαδή κάποιος έχει ανακαλύψει κάποιο μέρος-της, και το εξέθεσε με διαφορετικά λόγια· και η λίστα των ανθρώπων αυτών πηγαίνει πίσω ως τα αρχαία χρόνια.
| Προειδοποίηση: Πολλοί από τους διανοητές των οποίων οι απόψεις παρουσιάζονται παρακάτω συμπέραναν οτι ο χρόνος δεν υπάρχει. Αυτό έρχεται σε αντίθεση με την άποψη του παρόντος άρθρου, που θεωρεί οτι ο χρόνος είναι πραγματικός, αλλά υποστηρίζει οτι η ροή του χρόνου είναι μια νοητική ψευδαίσθηση· παρακαλώ διαβάστε τις ακόλουθες παραπομπές έχοντας αυτό υπόψη. |
-
Κατά τον 5ο αιώνα π.Χ., ο σοφιστής φιλόσοφος Αντιφών έγραψε στο έργο-του Περί αληθείας οτι: «Ο χρόνος δεν αποτελεί πραγματικότητα [υπόστασιν], αλλά μια έννοια [νόημα], ή μέτρο.» Ο Παρμενίδης (περίπου το 500 π.Χ.), ιδρυτής της Ελεατικής σχολής, προχώρησε ακόμη περισσότερο, υποστηρίζοντας οτι ο χρόνος, η κίνηση, και η αλλαγή είναι ψευδαισθήσεις. Η ιδέες του Παρμενίδη έγιναν ευρύτερα γνωστές από το μαθητή-του Ζήνωνα τον Ελεάτη (περίπου το 495 – 430 π.Χ.), που έθεσε τα περίφημα παράδοξά του σχετικά με το χρόνο, ισχυριζόμενος οτι η κίνηση είναι αδύνατη. Το πιο διάσημο από τα παράδοξά του είναι αυτό στο οποίο ο Αχιλλέας, ο θρυλικός ήρωας και ταχύς δρομέας, ξεκινά π.χ. 100 m πίσω από μια χελώνα, η οποία κινείται με το 1% της ταχύτητας του Αχιλλέα. Μέχρι τη στιγμή που ο Αχιλλέας διανύει 100 m, η χελώνα προχωρεί κατά 1 m· ώσπου ο Αχιλλέας να διανύσει αυτό το 1 m, η χελώνα προχωρεί κατά 1 cm· τη στιγμή που ο Αχιλλέας φτάνει αυτό το επιπλέον 1 cm, η χελώνα είναι ακόμα μπροστά-του κατά το 1/10 του mm· και ούτω καθεξής, επ’ άπειρον. Συνεπώς, ο Αχιλλέας δεν πρόκειται ποτέ να ξεπεράσει τη χελώνα. Παρόλο που σήμερα γνωρίζουμε που είναι η παγίδα,(14) τα παράδοξα του Ζήνωνα έπαιξαν το ρόλο-τους επί αιώνες, υπενθυμίζοντας στους φιλοσόφους πως δεν είναι καθόλου προφανές οτι ο χρόνος, η κίνηση, και η αλλαγή πρέπει να γίνουν δεκτά εκ προοιμίου ως κομμάτια της οντολογίας της πραγματικότητας.
-
Ο Πλάτων (περίπου το 427 – 347 π.Χ.) ήταν ο πρώτος που πρότεινε οτι αντιλαμβανόμαστε μόνο μια διαστρεβλωμένη εικόνα της πραγματικότητας, απλές “σκιές” αυτών που πραγματικά υπάρχουν στον κόσμο. Ο Πλάτωνας το έκανε αυτό μέσω της “αλληγορίας του σπηλαίου” στην Πολιτεία, Βιβλίο VII. Σε αυτήν, ο Σωκράτης ζητάει από το Γλαύκο (τον συνομιλητή-του) να φανταστεί οτι όλοι-μας ζούμε σε μια σπηλιά, και είμαστε δεμένοι με τέτοιο τρόπο ώστε μπορούμε μόνο να κοιτάμε τον τοίχο της σπηλιάς, ανήμποροι να στρέψουμε τα κεφάλια-μας. Μια φωτιά, την οποία δεν μπορούμε να δούμε, μαίνεται από πίσω και πάνω απ’ τα κεφάλια-μας, προβάλλοντας τις σκιές των αντικειμένων και των εαυτών-μας στον τοίχο της σπηλιάς. Έχοντας μεγαλώσει έτσι από τα παιδικά-μας χρόνια, εκλαμβάνουμε τις σκιές σαν να είναι τα αντικείμενα καθαυτά. Αλλά τώρα υποθέστε πως κάποιος ξεκλειδώνει και να χαλαρώνει τα δεσμά-μας, και μας οδηγεί έξω από τη σπηλιά, στο φως του ήλιου. Τότε θα νιώθαμε τα μάτια-μας να πονάνε, λόγω της ξαφνικής λαμπρότητας του φωτός, και θα χρειαζόμασταν κάμποσο χρόνο να συνηθίσουμε να βλέπουμε όχι απλές σκιές τώρα πια, αλλά τα αντικείμενα καθαυτά.
Ο Πλάτωνας, όντας ιδεαλιστής (σε αντίθεση με τους υλιστές), χρησιμοποίησε την αναλογία του σπηλαίου για να υποστηρίξει οτι πέρα απ’ τον κόσμο της άμεσης υλικής εμπειρίας υπάρχει ο κόσμος τον καθαρών και τέλειων ιδεών, τις ατελείς σκιές των οποίων συνήθως είμαστε περιορισμένοι να παρατηρούμε στη ζωή-μας. Αλλά ο μεγάλος φιλόσοφος ήρθε τόσο κοντά στην ιδέα οτι ο υλικός κόσμος είναι αυτός που διαφέρει και εμείς αντιλαμβανόμαστε μόνο διαστρεβλωμένες σκιές-του, που πιστεύω οτι δικαιούται τον τίτλο του πρώτου διανοητή που είδε τα όρια της ανθρώπινης νόησης, προχωρώντας έτσι χιλιάδες χρόνια μπροστά από την εποχή-του. (Το εάν ο ίδιος ο Σωκράτης συζήτησε πραγματικά την αλληγορία του σπηλαίου με κάποιον είναι ένα θέμα συζητήσιμο· ο Πλάτωνας συνήθως χρησιμοποιούσε το δάσκαλό του, το Σωκράτη, σαν ένα χαρακτήρα των διαλόγων-του, για να επιχειρηματολογήσει υπέρ ή κατά κάποιας φιλοσοφικής θέσης. -
Ο Γκότφριντ Βίλελμ φον Λάιμπνιτς (Gottfried Wilhelm von Leibniz, 1646 – 1716) ήταν ο πρώτος φιλόσοφος μετά τους Έλληνες που πρότεινε οτι ο χρόνος δεν υπάρχει, οτι είναι μια ψευδαίσθηση της ανθρώπινης διάνοιας. Παρόμοιες απόψεις είχε και ο Ιμμάνουελ Καντ (Immanuel Kant, 1724 – 1804). Ωστόσο, η ιδέα του χρόνου που συζητείται στο παρόν κείμενο δεν μπορεί να θεωρηθεί “του Λάιμπνιτς”, διότι ο Λάιμπνιτς πίστευε οτι ο χρόνος και ο χώρος δεν είναι πραγματικοί αλλά μέρη ενός εννοιολογικού συνόλου (μαζί με τον Αριθμό — π.χ. δείτε εδώ), ξανα-ανακαλύπτοντας έτσι τις ιδέες του αρχαίου Αντιφώντα (δείτε παραπάνω). Ο Λάιμπνιτς πίστευε οτι ο νους δημιουργεί και δίνει υπόσταση στο χρόνο και στο χώρο. Αντίθετα, η παρούσα άποψη θεωρεί οτι ο χώρος και ο χρόνος είναι πραγματικοί, αλλά ο δεύτερος μοιάζει πολύ περισσότερο με τον πρώτο απ’ ότι μας αφήνει να πιστεύουμε η νόησή μας. Αντίθετα με το Λάιμπνιτς, εδώ ο χώρος και ο χρόνος εκλαμβάνονται ως οντότητες ανεξάρτητες του ανθρώπινου νου, και είναι μόνο η ροή του χρόνου που προτείνεται οτι αποτελεί νοητική ψευδαίσθηση.
-
Το εγχειρίδιο του James Hartle Βαρύτητα (δείτε το στο Amazon) ήταν η κύρια πηγή που χρησιμοποίησα προκειμένου να ελέγξω τις περισσότερες ιδέες που συζητούνται στο παρόν. Είναι ένα θαυμάσιο κείμενο που δείχνει πώς η τετραδιάστατη χωροχρονική φυσική μπορεί να ειδωθεί απλά σαν γεωμετρία του τετραδιάστατου καμπύλου χώρου. Η μετατροπή της φυσικής σε γεωμετρία βρίσκεται στο επίκεντρο της παρούσας συζήτησης, και το βιβλίο του Hartle κάνει εξαιρετική δουλειά για το σκοπό αυτό.
-
Ο Julian Barbour έγραψε το βιβλίο Το τέλος του χρόνου: η επόμενη επανάσταση στη φυσική, το 1999 (δείτε το στο Amazon). Για να πω την αλήθεια, προσπάθησα να το διαβάσω αλλά δεν τα κατάφερα. Πέραν των εισαγωγικών κεφαλαίων, το βρήκα πολύ τεχνικό και πέρα από τις δυνατότητές μου. Διάβασα στο Amazon οτι και άλλοι εκφράζουν παρόμοιους προβληματισμούς, αλλά ένας αναγνώστης κάνει τις ακόλουθες ενδιαφέρουσες παρατηρήσεις:
«Βασικά, αυτό που κάνει ο Julian Barbour, δεν είναι τίποτα λιγότερο από μια ολοκληρωτική ανοικοδόμηση του συνόλου της φυσικής, με βάση την οπτική περί χρόνου του Λάιμπνιτς. Αρχικά δείχνει πώς η κλασική φυσική μπορεί τότε να κατανοηθεί. Έπειτα προχωράει να κάνει το ίδιο με την ειδική και γενική θεωρία της σχετικότητας του Αϊνστάιν. Αφού γίνει αυτό, προχωράει ακόμα και στην κβαντική μηχανική. Άραγε τα καταφέρνει; Νομίζω πως ναι. [...]
Η μόνη αντίρρηση σχετικά με την προσέγγιση του Julian Barbour είναι, ουσιαστικά, η ίδια που μπορείτε να αντιτάξετε στην ιδέα του Λάιμπνιτς περί χρόνου. Φιλοσοφικά μιλώντας, εάν ξεκινήσετε με την παραδοχή οτι δεν υπάρχει καμία πραγματική αλλαγή, και οτι όλη η μεταβολή είναι μια “ψευδαίσθηση”, που “υπάρχει μόνο στο νου”, τότε πρέπει να εξηγήσετε πώς προκύπτει αυτή η ψευδαίσθηση, χωρίς την εισαγωγή κίνησης ΟΠΟΥΔΗΠΟΤΕ. Όλες αυτές οι προσπάθειες έχουν αποτύχει.»
Δεν νομίζω οτι η άποψη του Barbour είναι τύπου Λάιμπνιτς (όχι, δεν λέει κάτι τέτοιο ο παραπάνω αναγνώστης), αλλά η απορία του αναγνώστη για το πώς μπορεί να προκύψει η ψευδαίσθηση χωρίς να εισάγουμε πουθενά την κίνηση απαντιέται εύκολα μέσω της αναλογίας του μουσικού δίσκου LP (που συζητήθηκε προηγουμένως στο κείμενο): η μουσική (κατ’ αντιστοιχία με τη νόηση, ή τη σκέψη) είναι μια έννοια της αντίληψης του χρόνου “κατά φέτες” μόνο. Όταν κάποιος βλέπει το LP συνολικά, η μουσική εξαφανίζεται, δεν υπάρχει πουθενά για να την αντιληφθούμε. Η φράση «η ροή του χρόνου είναι μια ψευδαίσθηση» σημαίνει οτι όταν θεωρήσουμε το χρόνο “κατά φέτες”, θα έχουμε νόηση και τη συνοδευτική-της ψευδαίσθηση της χρονικής ροής. Αλλά όταν θεωρήσουμε το χωροχρόνο ολιστικά, σαν σύνολο, δεν υπάρχει ψευδαίσθηση. Ο παραπάνω αναγνώστης θέλει να βρει την ψευδαίσθηση στην τετραδιάστατη ολιστική άποψη, όπου όμως δεν υπάρχει για να βρεθεί. Η ψευδαίσθηση προκύπτει μόνο όταν εισάγουμε την κίνηση, που συμβαίνει στην τριδιάστατη αντίληψη του χρόνου “κατά φέτες”.
Η αίσθηση που αποκομίζω είναι οτι το βιβλίο του Barbour εξηγεί τις λεπτομέρειες της φυσικής της παρούσας άποψης, χωρίς να υπεισέρχεται στις φιλοσοφικές συνέπειες· τις οποίες, ωστόσο, βρίσκω πολύ πιο σημαντικές. (Διαθέτουμε ένα αρκετά επιτυχημένο μοντέλο του χωροχρόνου στη φυσική, στο κάτω-κάτω, μοντέλο που μοιάζει να μη χρειάζεται επισκευή προς στο παρόν.)
Τώρα, πρέπει να ομολογήσω κάτι: έγραψα το υπόλοιπο αυτής της ενότητας με μισή καρδιά. Ο λόγος είναι οτι η βιβλιογραφία που με βοήθησε να αποκρυσταλλώσω τις παραπάνω σκέψεις είναι αυτή που έχω ήδη αναφέρει στην §2, μαζί με ένα μεγάλο αριθμό βιβλίων που συνέβαλαν στις γενικές-μου γνώσεις. Αλλά εάν δεν αναφέρω τη βιβλιογραφία που ακολουθεί, κάποιοι αναγνώστες θα μου την επισημάνουν: «Α, μα δεν έχεις διαβάσει το βιβλίο του τάδε και του δείνα;» Μπορεί και να τα έχω διαβάσει (ή αυτά ή περιγραφές-τους), αλλά δεν συνεισέφεραν πραγματικά σε κάτι ώστε να αναπτυχθούν οι παραπάνω ιδέες — τουλάχιστον έτσι νομίζω. Σε κάθε περίπτωση, θα κάνω το προληπτικό χτύπημά μου, καταγράφοντας τα έργα τα οποία γνωρίζω (κάποια από αυτά σχετιζόμενα με το θέμα-μας αμυδρά μόνο):
-
Ο John Ellis McTaggart έγραψε το “Η μη-πραγματικότητα του Χρονου” (The Unreality of Time) το 1908 (δημοσιεύτηκε στο Mind: A Quarterly Review of Psychology and Philosophy 17 [1908]: 456–473). (Διαβάστε-το εδώ, στα αγγλικά.) Σ’ αυτό, ο McTaggart πρότεινε τους όρους “Α σειρά” και “Β σειρά”, όπου με την “Α σειρά” εννοούσε την ακολουθία των γεγονότων όπως την αντιλαμβανόμαστε από την δική μας οπτική (“από τα μέσα”, σαν να λέμε), η οποία περιλαμβάνει ένα “τώρα”· ενώ με τη “Β σειρά” εννοούσε την ολιστική άποψη των ακολουθιών των γεγονότων, όπου δεν υπάρχει το προνομιούχο “τώρα”, αλλά όπου μπορούμε να συγκρίνουμε γεγονότα χρονολογικά και να πούμε οτι αυτό το γεγονός έγινε πριν από τούτο, κ.ο.κ. Ο McTaggart προχωρά στο άρθρο-του, αρχικά για να δείξει οτι η “Α σειρά” είναι πιο θεμελιώδης από τη “Β σειρά” για την περιγραφή του χρόνου· και έπειτα για να δείξει οτι δεν μπορεί να υπάρξει “Α σειρά”, οπότε συμπεραίνει την ανυπαρξία του χρόνου. Δείχνει — ή νομίζει πως δείχνει, τέλος πάντων — οτι δεν μπορεί να υπάρξει “Α σειρά” χάρη στην παρατήρηση οτι σε κάθε γεγονός πρέπει να εκχωρούνται τρείς αμοιβαία ασύμβατες ετικέτες: κάθε γεγονός είναι αρχικά στο μέλλον, αργότερα γίνεται παρόν, και τελικά περνά στο παρελθόν. Ο McTaggart νομίζει οτι δεν μπορούμε να δώσουμε τρεις αμοιβαία ασύμβατες ετικέτες σε ένα μοναδικό γεγονός, οπότε δεν μπορεί να υπάρξει καμία “Α σειρά”.
Αλλά αυτό εμένα μου ακούγεται σαν σοφιστεία. Γιατί δηλαδή πρέπει μόνο μία χρονική ετικέτα να δοθεί σε κάθε γεγονός; Γιατί οι ετικέτες “παρελθόν”, “παρόν” και “μέλλον” είναι αμοιβαία ασύμβατες; Είναι συμβατές εάν εκχωρήσουμε την κάθε μία σε ένα διαφορετικό χρόνο. Ο McTaggart νομίζει οτι δεν μπορούμε να το κάνουμε, επειδή ο σκοπός-μας ήταν να εξηγήσουμε το χρόνο σε πρώτη φάση, οπότε δεν μπορούμε να χρησιμοποιήσουμε το χρόνο για να κάνουμε τις ετικέτες συμβατές, αλλιώς καταλήγουμε σε φαύλο κύκλο. Αλλά δεν χρειάζεται να εξηγήσουμε το χρόνο· μπορούμε να τον θεωρήσουμε ως θεμελιώδη. Ο McTaggart δεν θέλει να αποδεχθεί το χρόνο ως θεμελιώδη, θέλει να τον εξηγήσει, και γιαυτό πέφτει μέσα στη λογική άβυσσο. Σκέφτεται ως εξής: «Κάθε τί που ορίζεται με όρους απλών εννοιών δεν είναι θεμελιώδες· θέλω να ορίσω το χρόνο με όρους απλούστερων εννοιών· αλλά δεν μπορώ, επομένως [αντί να καταλήξω στο οτι ο χρόνος είναι θεμελιώδης] ο χρόνος είναι ανύπαρκτος!» Βγάζει νόημα; Δεν νομίζω, γιατί σημαίνει πως οτιδήποτε το θεμελιώδες — ως εκ τούτου μη ορισμένο — πρέπει να είναι ανύπαρκτο! Σήμερα γνωρίζουμε οτι μπορούμε να θεωρήσουμε το χρόνο θεμελιώδη, και να επινοήσουμε μια λογική με την οποία μπορούμε να μιλάμε με συνέπεια για χρονικά γεγονότα μέσω των διάφορων “χρονικών λογικών” (“temporal logics”), οι οποίες είναι ειδικές περιπτώσεις της τυπικής λογικής. Δεν κατηγορώ τον McTaggart για την άγνοιά του σχετικά με αυτά κατά το μακρινό 1908, αλλά δεν μπορώ να καταλάβω και την επιμονή μερικών σύγχρονων φιλοσόφων στο να αναφέρονται στην εργασία του McTaggart σαν μια ουσιαστική συνεισφορά πάνω στο θέμα του χρόνου.
-
Το βιβλίο του D. H. Mellor, Real Time II (1998, Routlege· θα το βρείτε εδώ, στο Amazon). Λοιπόν, αυτό που μπορώ να πω για το βιβλίο του Mellor είναι οτι… το διάβασα. Μάλιστα! Τώρα, αν με ρωτήσετε τί θυμάμαι από αυτό, θα σας κοιτάξω ανέκφραστος για λίγο, ερευνώντας βαθειά στη μνήμη μου… Θυμάμαι πως διάβασα για την ασυμμετρία του χρόνου, για το γεγονός οτι έχει κατεύθυνση, και για το ερώτημα περί ισοτροπίας / ανισοτροπίας-του. Αλλά είχα διαβάσει για αυτές τις έννοιες και αλλού. Α, ναι, ο Mellor παίρνει τον McTaggart στα σοβαρά. Εντάξει, καλύτερα να σταματήσω. Διαβάστε το βιβλίο αν ενδιαφέρεστε για ένα σοβαρό φιλοσοφικό δοκίμιο επί του σοβαρού θέματος του χρόνου.
-
Το βιβλίο του Palle Yourgrau, A World Without Time: The Forgotten Legacy of Gödel and Einstein (2005, Basic Books· στο Amazon). Βρίσκω οτι το βιβλίο αυτό απλώς αγγίζει επιφανειακά το θέμα-μας (παρά τον πιασάρικο τίτλο-του, για τον οποίο και έσπευσα να το αγοράσω). Διαβάστε τις σελίδες 128 – 131, με τίτλο: «Ο διαλεκτικός χορός του Gödel με τον χρόνο» (“Gödel’s Dialectical Dance with Time”), για να καταλάβετε ποια είναι η ουσία του βιβλίου. Σε αυτές τις σελίδες, ο Yourgrau λέει:
«Οι εξισώσεις της γενικής σχετικότητας επιτρέπουν εναλλακτικές λύσεις, εκ των οποίων η κάθε μία καθορίζει ένα πιθανό σύμπαν, ένα σχετικιστικά δυνατό κόσμο. Οι λύσεις σε αυτές τις σύνθετες εξισώσεις είναι σπάνιες, αλλά ο Gödel αμέσως ανακαλύπτει ένα σχετικιστικά δυνατό σύμπαν (στη πραγματικότητα, ένα σύνολο από αυτά) — γνωστό πλέον ως το σύμπαν του Gödel — στο οποίο η γεωμετρία του κόσμου είναι τόσο ακραία που περιέχει χωροχρονικά μονοπάτια αδιανόητα σε πιο οικεία σύμπαντα σαν το δικό-μας. Σε ένα τέτοιο σύμπαν του Gödel, αποδεικνύεται οτι υπάρχουν κλειστές χρονοειδείς καμπύλες τέτοιες ώστε αν ταξιδέψεις αρκετά γρήγορα, μπορείς, αν και κατευθυνόμενος προς το τοπικό-σου μέλλον, να φτάσεις στο παρελθόν. Αυτοί οι κλειστοί βρόχοι ή κυκλικά μονοπάτια έχουν ένα πιο οικείο όνομα: ταξίδι στο χρόνο. Αλλά εάν είναι δυνατό σε τέτοιους κόσμους, ισχυρίζεται ο Gödel, να επιστρέψει κάποιος στο παρελθόν-του, τότε αυτό που ήταν παρελθόν δεν παρήλθε ποτέ. Αλλά ένας χρόνος που ποτέ δεν παρέρχεται πραγματικά, δεν μπορεί να θεωρηθεί ως πραγματικός, διαισθητικός χρόνος. Η πραγματικότητα του ταξιδιού στο χρόνο στο σύμπαν του Gödel σηματοδοτεί την εξωπραγματικότητα του χρόνου. Για ακόμα μια φορά, ο χρόνος εξαφανίζεται.
Αλλά ο χορός δεν έχει τελειώσει. Γιατί το σύμπαν του Gödel, εν τέλει, δεν είναι ο πραγματικός κόσμος, αλλά μόνο ένας απ’ τους πιθανούς. Δικαιούμαστε πραγματικά να συμπεράνουμε την ανυπαρξία του χρόνου σε αυτό τον κόσμο από την απουσία του σε ένα απλώς πιθανό σύμπαν; Με μια λέξη, ναι. Ή τουλάχιστον έτσι ισχυρίζεται ο Gödel. Εδώ κάνει το τελικό, το πλέον λεπτό και άπιαστο βήμα· αυτό, απ’ το πιθανό στο πραγματικό. [Το επιχείρημα του Gödel είναι οτι] εάν ένα μαθηματικό αντικείμενο είναι όντως πιθανό, αναγκαία, ως εκ τούτου, είναι πραγματικό. Αυτό συμβαίνει επειδή αυτό που υποχρεωτικά υπάρχει δεν μπορεί να υπάρξει καθόλου εκτός και αν υπάρχει σε όλους του πιθανούς κόσμους. […]»Κρούει αυτό το τελευταίο επιχείρημα κάποιον κώδωνα στο νου-σας; Τι θα λέγατε γι’ αυτό: «Οντολογικό επιχείρημα για την ύπαρξη του Θεού». Ναι, σωστά; Εάν ο Θεός είναι όντως πιθανός, είναι πραγματικός (ο Yourgrau το αναφέρει έπειτα αυτό, αυτολεξεί). Αυτό είναι το πλέον γελοιωδώς ιδεαλιστικό επιχείρημα που άκουσα ποτέ-μου, βασιζόμενο στην ιδέα «Θέλω να είναι αλήθεια ανεξάρτητα του πόσο χαζό ακούγεται». Ούτε ο Πλάτωνας, ο Μέγας Ιδεαλιστής, δεν τόλμησε να πει τέτοιες ανοησίες. Ώστε εάν όντα με πόδια που βλασταίνουν απ’ τα ρουθούνια-τους και φύλλα χασίς που κρέμονται απ’ τις θηλές-τους είναι όντως πιθανά, τότε είναι πραγματικά. Μμμάλιστα. Επιπλέον, διαβάζουμε:
«Στην περίπτωση του σύμπαντος-του Gödel, ο ίδιος εξήγησε οτι αφού αυτός ο πιθανός κόσμος διέπεται από τους ίδιους φυσικούς νόμους που ισχύουν στον πραγματικό κόσμο — διαφέροντας από τον κόσμο-μας μόνο στην υπό ευρεία κλίμακα κατανομή ύλης και κίνησης — δεν μπορεί να ισχύει οτι ενώ ο χρόνος αποτυγχάνει να υπάρξει σε αυτό τον πιθανό κόσμο, είναι παρών στον δικό μας. Για να το αρνηθούμε αυτό, επιχειρηματολόγησε ο Gödel, θα έπρεπε να ισχυριστούμε οτι “το αν υπάρχει ή όχι ένα αντικειμενικό πέρασμα χρόνου (δηλ. το αν υπάρχει ή όχι χρόνος με την συνηθισμένη έννοια) εξαρτάται από τον ιδιαίτερο τρόπο με τον οποίο η ύλη και η κίνησή της είναι διατεταγμένες σ’ αυτόν τον κόσμο.” Ασχέτως αν αυτό δεν θα οδηγούσε σε μια οριστική αντίφαση, ισχυρίστηκε: “μολοταύτα, μια φιλοσοφική άποψη που οδηγεί σε τέτοιες συνέπειες δύσκολα μπορεί να θεωρηθεί ως ικανοποιητική.” Αλλά αποδεικνύεται οτι ο χρόνος αποτυγχάνει να υπάρξει στο σύμπαν του Gödel. Δεν μπορεί, συνεπώς, να υπάρχει στο δικό-μας. Το τελευταίο βήμα έγινε· η αυλαία έπεσε: ο χρόνος όντως εξαφανίζεται.»
Αν καταφέρατε να μην αποσπαστεί η προσοχή-σας από τις μελοδραματικές και θεατρικές γραμμές του κλεισίματος του Yourgrau, θα δείτε οτι προσπαθεί να διατυπώσει κάποιο επιχείρημα εκεί. Αλλά εξαφανίζεται πραγματικά ο χρόνος στο σύμπαν του Gödel; Γιατί εξαφανίζεται ο χρόνος εάν υπάρχουν κλειστοί βρόχοι σε αυτά τα σύμπαντα; Αυτό δεν μου ήταν και τόσο ξεκάθαρο μετά την ανάγνωση του βιβλίο του Yourgrau. Επιπλέον, γιατί αν κάτι δεν υπάρχει σε ένα από τα σύμπαντα του Gödel τότε δεν μπορεί να υπάρξει και στο δικό-μας; Αν οι ελέφαντες δεν μπορεί να υπάρξουν σε ένα σύμπαν του Gödel, τότε αυτό σημαίνει οτι και το σύμπαν-μας δεν μπορεί να έχει ελέφαντες; Τί είδους παράλογη λογική είναι αυτή;
-
Η πραγματεία του George F R Ellis, Physics in the Real Universe: Time and Spacetime (διαβάστε το εδώ, σε pdf). H πραγματεία του Ellis κάνει μια λανθασμένη υπόθεση: οτι, τάχα, η ιδέα ενός μονολιθικού σύμπαντος «βασίζεται σε χρονικά αντιστρέψιμους νόμους μικροφυσικής, οι οποίοι αποτυγχάνουν να συλλάβουν ουσιώδη χαρακτηριστικά της χρονικά μη-αντιστρέψιμης μακρο-φυσικής συμπεριφοράς και της ανάπτυξης των αναδυόμενων πολύπλοκων συστημάτων, συμπεριλαμβανομένης και της ζωής, τα οποία υπάρχουν στο πραγματικό σύμπαν», όπως διαβάζουμε στη σύνοψη. Όμως η άποψη περί μονολιθικού σύμπαντος δεν περιορίζεται σε χρονικά αντιστρέψιμους νόμους της κλασικής και σχετικιστικής φυσικής, αλλά περιλαμβάνει τα πάντα στο σύμπαν, συμπεριλαμβανομένης και της ζωής (και, όπως κόπιασα να εξηγήσω, της νόησης). Ο κόσμος, με τη βιολογία-του και όλα τα σχετικά, απλώς είναι. Η χρονική αντιστρεψιμότητά του συμπεριλαμβάνεται κι αυτή. Αυτό που καταλαβαίνω είναι οτι ο Ellis δημιουργεί και επιτίθεται σε ένα έωλο επιχείρημα.
-
Το κλασικό βιβλίο του Paul Davies: About Time: Einstein’s Unfinished Revolution (1995, Simon & Schuster· στο Amazon). Η καλύτερη εξήγηση του σχετικιστικού παραδόξου των διδύμων, αλλά πέραν αυτού… Ο Davies γράφει με έναν ευανάγνωστο και διασκεδαστικό τρόπο. Το βιβλίο είναι επίσης μια καλή εισαγωγή στη σχετικότητα.
-
Το κλασικό βιβλίο του Stephen Hawking: A Brief History of Time (1996, Bantam Books· στο Amazon). Εισαγωγικό και στοιχειώδες. Διαβάστε το μόνο αν είναι απ’ τα πρώτα-σας πάνω στο θέμα, ή αν σας αρέσουν τα κλασικά. (Το εντάσσω σε αυτή τη λίστα μόνο και μόνο επειδή ο κόσμος είναι μεγάλος, το διαδίκτυο παγκόσμιο, και κάποιος σίγουρα θα μου το συστήσει αν δεν το αναφέρω εδώ.)
ΤΟ ΥΠΟΛΟΙΠΟ ΤΟΥ ΠΑΡΟΝΤΟΣ ΚΕΙΜΕΝΟΥ
ΒΡΙΣΚΕΤΑΙ ΣΤΟ ΣΤΑΔΙΟ ΤΗΣ ΜΕΤΑΦΡΑΣΗΣ,
ΚΑΙ ΘΑ ΓΙΝΕΤΑΙ ΣΤΑΔΙΑΚΑ ΔΙΑΘΕΣΙΜΟ ΣΤΟ ΜΕΛΛΟΝ
4. Feedback
How much of the above is true? I am interested
in receiving feedback. But before contacting me to complain that you don’t feel you have disappeared
at all, please make sure you have understood the contents of this
page adequately enough, perhaps having some insight that eluded
me. If you think that this is the case, I’ll be more than happy
to learn why you still exist. ![]() However, this page is not a blog, so I will not
include here every random opinion, but only those that, in my
judgment, are possible objections to the disappearance act. I
will present such opinions anonymously only.
However, this page is not a blog, so I will not
include here every random opinion, but only those that, in my
judgment, are possible objections to the disappearance act. I
will present such opinions anonymously only.
![]() 1.
A reviewer, a professor of physics (I think), brought up the
following objection: “[T]his ‘argument’ does not have
anything uniquely pertinent to special relativity as compared to
any other theory.” What the professor meant is that the same
arguments as the ones expounded above could also be used without
reference to Einstein’s relativity. For example, I could be
using a 4-D Galilean space, i.e., a space with Euclidean
geometry, and the arguments would be identical. Relativity is
irrelevant, the professor said.
1.
A reviewer, a professor of physics (I think), brought up the
following objection: “[T]his ‘argument’ does not have
anything uniquely pertinent to special relativity as compared to
any other theory.” What the professor meant is that the same
arguments as the ones expounded above could also be used without
reference to Einstein’s relativity. For example, I could be
using a 4-D Galilean space, i.e., a space with Euclidean
geometry, and the arguments would be identical. Relativity is
irrelevant, the professor said.
I don’t think so. A 4-D Galilean physics, i.e., one based on Euclidean geometry, does not explain why we perceive one of the dimensions (which we call “time”) as special. Why that dimension appears different? Why one of the four? Indeed, the metric in Euclidean 4-D space is given by the formula: d2 = x2 + y2 + z2 + t2, where x, y, and z stand for the three spatial dimensions, and t for the temporal one. But all four dimensions show a complete symmetry in this formula. We can freely interchange t with any of the x, y, z in this formula, and nothing will change; for example, we can write d2 = x2 + t2 + z2 + y2, and christen “spatial” the dimensions x, t, and z, and “temporal” the dimension y. In contrast, in 4-D Minkowskian geometry, the metric is: d2 = x2 + y2 + z2 – t2, which tells us very explicitly that one of the four dimensions differs from the other three: it is the dimension that has the minus sign in the formula of the metric; that is the dimension we perceive as “time”, and to which we ascribe temporal properties. Why? because if we summarize x2 + y2 + z2 by s2 (i.e., if s is our familiar 3-D spatial length), then we get d2 = s2 – t2. Now if we set d = 0, which means that we are interested in finding out which spatio-temporal coordinates result in simultaneous 4-D events (see also the discussion in §1.6), then we obtain |s| = |t|, or: the length of space equals the length of time for such events. This is possible only in the Minkowskian geometry of special relativity.
Also, relativity is relevant in another important way in the above disappearance act: It is because of the relativistic relation of mass and energy that one can conceive of “plasmoids”, placing them close to the opposite end of the mass–energy range from the one we occupy: i.e., the plasmoids have mostly kinetic energy but not much inertial mass, whereas we have mostly inertial mass but not much kinetic energy. None of the above arguments would hold if relativity were missing from the picture.
![]() 2.
The same reviewer objected by arguing that Minkowskian geometry describes a
spacetime devoid of mass and energy, and spent about two full pages to tell me
(in various rephrasings and word-permutations of the same idea) that general
relativity does away with Minkowski spacetime, and instead employs Friedman
spacetime, in which we live, since there is not just empty spacetime, but also
mass and energy in our world. Thus, since I do not make reference to Friedman
spacetime and general relativity, the professor thought, my arguments are
irrelevant in the real world. Specifically the professor wrote:
2.
The same reviewer objected by arguing that Minkowskian geometry describes a
spacetime devoid of mass and energy, and spent about two full pages to tell me
(in various rephrasings and word-permutations of the same idea) that general
relativity does away with Minkowski spacetime, and instead employs Friedman
spacetime, in which we live, since there is not just empty spacetime, but also
mass and energy in our world. Thus, since I do not make reference to Friedman
spacetime and general relativity, the professor thought, my arguments are
irrelevant in the real world. Specifically the professor wrote:
“The most basic misunderstanding of Einstein’s relativity theory underlying this article is that the author does not seem to know that Minkowski spacetime is the vacuum solution to the field equations of the general theory of relativity, implying that Minkowski spacetime cannot contain matter, observers and the like. But the author’s article is about a Minkowski spacetime that is posited as containing matter, motion, observers, etc., and the author is attempting to derive conclusions about space and time from this self-contradictory assumption (viz., that there is matter, motion, observers, etc. in a universe whose metric, line element and symmetry group [the Poincare group] precludes the presence of matter, motion, observers, etc.”
Fine. (Well, not fine: I am not just an “author”
to be reviewed, dear professor, but the great magician Harry
Foudini, as I already announced in the preface; and you will
disappear, nonetheless, for all your laudable efforts.
![]() ) However,
the professor missed a tiny yet crucial detail: nothing in this article requires
that space-time be flat, thus described by the Minkowskian geometry of special
relativity, and not curved, thus described by Friedman space-time. Let’s be more
specific and explicit:
) However,
the professor missed a tiny yet crucial detail: nothing in this article requires
that space-time be flat, thus described by the Minkowskian geometry of special
relativity, and not curved, thus described by Friedman space-time. Let’s be more
specific and explicit:
-
Special relativity can be seen as the geometry of flat 4D space-time.
-
General relativity can be seen as the geometry of curved 4D space-time; where, of course, what curves space-time is the presence of mass–energy.
Now, the basic observation that led to this article is not that 4D space-time is flat, but that time is another dimension on par with the three dimensions of space; i.e., that space and time are the same “stuff”; i.e., that s = t; and this holds whether space-time is flat or curved; it holds both in special and in general relativity. Thus, the professor’s remark that Minkowskian geometry (flat space-time) is a prerequisite for reaching the conclusions that we reached is simply not true.
Still, however, there is something worth pondering about, implied by the professor’s objection: if space-time is curved due to the presence of mass, why do we use the Minkowskian geometry of flat space-time to reason at all about observers, who have mass? Why not using general relativity and Friedman space-time, and thus avoid objections such as the above?
Because even though generally space-time is curved (and thus general relativity applies), locally the curved space-time is flat (barring singularities, such as black holes). This follows from the “equivalence principle” (e.g., see Hartle, §6.3), which says that the results of experiments that are done in sufficiently small space and that last for sufficiently short time cannot be distinguished from the results of the same experiments done in an inertial frame. Mathematically, this means that the space-time which is curved due to the existence of mass is smooth and continuous, and everywhere differentiable (again, excluding singularities). Thus, if we have a general metric gαβ(x) in some system of coordinates (I’m following Hartle’s notation, see his §7.4), then it is possible that for every point (or “event”) P of space-time we can define new coordinates x΄, such that: g΄αβ(x΄P) = diag(–1,1,1,1), which is the Minkowskian metric of flat space-time. This requirement is one of the assumptions of general relativity, and implies that at every point P there are three spatial coordinates and one temporal, whether mass exists at P or not. But what does all that mean practically, for us observers?
It means that we human observers, with the negligible masses of our environment, live in a world that’s a special case of the general one. We don’t walk on the surface of a neutron star, nor do we navigate in the vicinity of a black hole. Our world is essentially flat, devoid of mass and energy, at least of the amount of mass–energy that would make space-time truly (perceptibly) curved, and Friedman’s generalized solution relevant and indispensable in human cognition. Thus, given the parameters of the world in which we evolved, Minkowski space-time is still the space-time of our environment to an excellent approximation (although, as discussed earlier, we perceive it as an even simpler one: as Euclidean 3-d space + time). The vacuum solution to the field equations of general relativity is precisely what gives rise to our cognition; and it is the reason why Einstein arrived first at special relativity with its Minkowskian space-time: because that’s what we get under the assumption that there isn’t much mass around, and thus that space-time is locally not curved. General relativity might be “more correct” than the special one, but it is not particularly helpful in explaining our perceptual and other cognitive properties. In a sense, general relativity is an overkill for cognition, “too much” for us, tiny human observers — in a way reminiscent of the one in which quantum mechanics is too remote from our ordinary experience (read this article of mine on that subject).
The bottom line is: Minkowskian geometry is used in this text to explain not the universe itself, but our cognition, our perception of the universe and its properties; to explain not time itself, but our perception of time.
![]() 3. Another reader’s
objection was based on more philosophical grounds. The reader
thought: so what if it is possible to unify time and space,
eliminating the temporal properties of time; that it is possible
does not imply that it has to be thus. I might have
shown that the flow of time can possibly be a
cognitive illusion, but this does not make it an
illusion. It could still be the case, according to that reader’s
opinion, that the flow of time is real (i.e., we are 3-d spatial
beings who are presented with events of the future, time-slice
after time-slice), and that the cognitive illusion suggested in
this text is a mere curiosity: a possibility, but not the
reality.
3. Another reader’s
objection was based on more philosophical grounds. The reader
thought: so what if it is possible to unify time and space,
eliminating the temporal properties of time; that it is possible
does not imply that it has to be thus. I might have
shown that the flow of time can possibly be a
cognitive illusion, but this does not make it an
illusion. It could still be the case, according to that reader’s
opinion, that the flow of time is real (i.e., we are 3-d spatial
beings who are presented with events of the future, time-slice
after time-slice), and that the cognitive illusion suggested in
this text is a mere curiosity: a possibility, but not the
reality.
Originally (up to Oct. 2007), I had given an answer for the above objection in this page. My answer was based on the notion that the idea of time-flow-as-cognitive-illusion makes more sense from the point of view of philosophy and physics, because it results in a simplification (it gets rid of notions such as time-flow, past, present, future, etc.), and that the more complex (but, alas, so familiar!) alternative should be rejected by appeal to Occam’s razor. (I even referred the reader to a justification for Occam’s razor, see below.) But later another reader agreed with the first one — in spite of my answer — telling me that, yes, a possibility does not make a certainty. So I thought, wait a minute, can this be a matter of personal preference? Can someone say, “I prefer this because it chimes better with my intuition!”? There must be some objective way to decide which view is real.
Upon further consideration I believe I found an inherent flaw in the above reader’s view. Now, I’ll explain what the flaw is immediately, but I don’t want to trash completely my earlier reply, because there were some interesting (to others, I hope, not just to me) comments there. So I’ll proceed with my newer reply first, and after that I’ll enclose my earlier reply in a box (find it further below), for the interested reader to look at. (A link to a justification for Occam’s razor is given there.)
So: according to that reader’s objection, it could be that we are 3-d beings who are presented with events, time-slice after time-slice. Yea, why not?
Not, because this works in a Euclidean, wrong view of spacetime. Spacetime is relativistic, and this has been shown with countless experiments. I’ll explain.
Let’s first see what a Euclidean “time-slice after time-slice” view of reality means. It means that now our 3-d world looks like this; the next moment, our 3-d world looks like that; then, a moment after that, it has yet a different configuration; and so on. Normally I should draw these 3-d slices by placing them next to each other, and assume that time presents them to us from left to right, one after the other. But because it is impossible to draw 3-d chunks of space next to each other, what authors usually do to illustrate this idea is to reduce the dimensions of our space from 3 to 2; so imagine that ours is a 2-d spatial universe, looking like a flat sheet of paper. Now we can stack such 2-d slices next to each other, as Figure 4.1 shows, imagining that each slice is our whole universe, and is presented to us at a given time t1; the next moment, t2, the slice following it is presented; and so on.
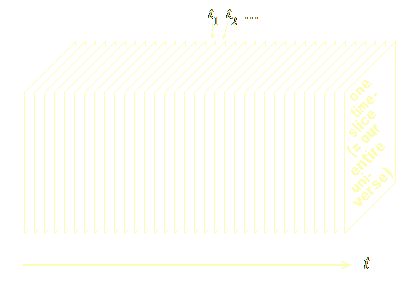
Figure 4.1: View of the world as it appears to those who raise the present objection
But, as I mentioned above, the view of the world as shown in Figure 4.1 is wrong. Here is why: suppose you are standing somewhere, and a friend of yours is moving with a constant speed relative to you (Figure 4.2). Then your friend is perceiving different time-slices of the world than those that you perceive. Before Einstein, with the physics of Newton and the geometry of Euclid, people thought that everybody perceives the same time-slices, as in Figure 4.1. But after Einstein, with relativity, we learned that the situation in reality is different: you and your moving friend perceive time-slices as shown in Figure 4.2.
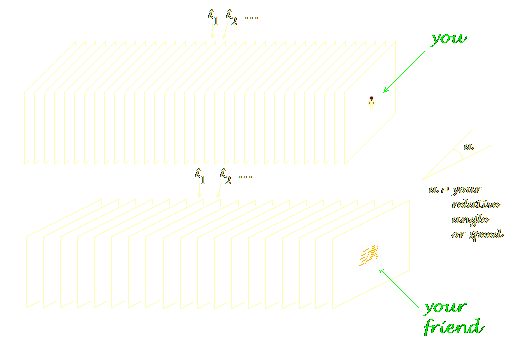
Figure 4.2: Slices are different if observers move relative to each other
The time-slices of the universe that you and your friend perceive are drawn at a relative angle a in the figure, and this angle is correlated with your relative speed (not exactly proportionally; but for the figure to make good sense we can say that as your relative speed approaches c the angle a approaches 90°).
So if the universe is “served” slice after slice, it is obviously served differently to each moving observer.
It gets more complicated than this, but let’s stop for a minute and ponder: if you feel that the “now” is one of those time-slices, which part of yourself perceives that now-slice? If you move your arm relative to your head, won’t your moving arm be in a different time-slice than your head? And where is the “you” that experiences the slice, the “now”? Are “you” in your head, excluding your moving arm? Are “you” at a point inside your brain? Any neurologist or cognitive scientist will tell you that there is no such point in your brain where the “I” resides; all information in the brain is distributed. The idea that the “I” occupies a specific point in space is unscientific, baseless. So you cannot identify the “now” that “you” just experienced with a particular time-slice of the universe, because if you take any time-slice you don’t know where to position the “you” with respect to that slice.
But, as I said, it gets more complicated than that. Figure 4.2 concerns observers moving relative to each other with constant speed. But in reality observers move by accelerating and decelerating. When you de-/accelerate, the time-slices of Figure 4.2 will acquire local dents. Your friend’s slices would have dents, too, and so would all the slices of all the billions of people on Earth, so the slices would mix and intermingle with each other. Further, the farther moving observers are from each other in space, the more their slices differ (see Greene,[1] pp. 132–139). If there are observers in the Andromeda Galaxy (or if your descendants travel there one day in the distant future), they would get completely different slices from you. Who, or what mechanism “serves” all those slices to all those observers? And who qualifies as an observer in the first place? Do all the billions of people on Earth count as observers to be served with slices? Don’t animals count? Isn’t your pet an observer? A baby? When does a baby become an observer? Starting as a one-cell creature, I suppose you’d agree that that is not an observer — it’s a potential one, but a single-celled creature does not observe anything yet — lest you are willing to admit this for every cell of your body. So when, at which magic moment does a baby acquire the status of an observer? Apparently there is no such magic moment, which means that the notion of “observer” cannot be defined in a sensible way; and this means that the notion that the universe is served slice-after-slice to observers cannot make much sense either.
OK, the above is my newer reply, and hopefully the final one. However, my earlier reply is shown in the box, below:
| I repeat, this is my earlier reply to the above
objection; a reply that I now consider insufficient, but
still including some hopefully interesting points: I suppose it could be as the reader suggested (and as virtually every person in this world intuitively feels is the case). I cannot prove that an illusion is going on. I can only suggest that (unfortunately) the idea of a cognitive illusion makes more physical sense, in the same way that the idea that the Earth and other planets orbit the Sun makes more physical sense than the idea that the Earth is immobile and all other planets, including the Sun, rotate around it on the celestial sphere (or spheres) in the course of a 24-hour period. The latter idea is a cognitive illusion; the former is reality. However, there are reasons for which the analogy I just brought up breaks down: we can perform a number of experiments and verify whether the Earth rotates around the Sun or whether the Sun (and everything else) rotates around the Earth. For example, if the Earth rotates around the Sun in the course of one year (as indeed it does), then we must be experiencing an extremely weak “centrifugal” force with a direction perpendicular to the tangent to the Earth’s orbit, away from the Sun, and this force must be measurable with some extremely sensitive instrument. Alternatively, we can conclude the correctness of the Copernican system (and the demise of the Ptolemaic one) with a simple thought: if the Earth is immobile and the planets rotate around the Earth in the course of a 24-hour period, then it turns out (as we can find out after a few simple calculations) that the planet Neptune — and everything that stands at a greater distance — must be rotating around Earth at a speed greater than the speed of light (a “superluminal” speed); but no object with mass greater than zero can move at a superluminal speed; therefore, by making use of modern knowledge, we can conclude with an armchair argument that the Ptolemaic system does not hold any water. Fine; so, could there be some experiment, or even thought experiment, that could tell the cognitive illusion idea and the “intuitive physics” (3d-space + 1d-time) apart? There might be, but at present I am not aware of any. A good reason that I have for suggesting that the cognitive illusion idea is the correct one is an appeal to the continuation of economy in physics. By this, I mean the following: even if there were no experiments (real or of thought) to make to tell the Copernican and Ptolemaic systems apart, still the former would be preferable because it is more economical than the latter: it describes nature in fewer and simpler terms. Our preference for the Copernican system is a typical application of Occam’s (or Ockham’s) razor: “Entities should not be multiplied needlessly”. The introduction of countless spheres-within-spheres and the complexity of the epicycles that the Ptolemaic system requires are cut off by Occam’s razor and replaced by the simpler Copernican (actually Keplerian) ellipses. Now, the cognitive illusion idea does not make such a dramatic reduction in complexity compared to the “intuitive physics”, I admit that much. But it causes some simplifications, nonetheless. Specifically, the intuitive physics uses two qualitatively different notions: space and time (note that even though general relativistic physics treats space and time as one idea, spacetime, what I mean by “intuitive physics” is the way time is presented in college physics textbooks: as an entity distinct from space), whereas the cognitive illusion idea does away with the need to talk about time as separate from space. Essentially the cognitive illusion explains why relativity deals with a unified spacetime and not with 3d-space + 1d-time; it also explains why time appears symmetric in physics formulas (Greene’s puzzlement): because it is locally symmetric, and it is only our cognition which gives us the illusion that time “flows” in one direction. (Why it is the direction we perceive and not the opposite one is the subject of this page.) There is at least one more sense in which the cognitive illusion idea is more economical than intuitive physics: the latter, with its “flow” of time, implies some kind of “speed” by which the time “flows” (a topic discussed earlier), and one is left wondering, why time is sensed as flowing at this particular “speed” and not some other one? Why is its “speed” sensed as uniform, why does it not sometimes speed up, and other times slow down? The cognitive illusion tells us that there is no such thing as flow and speed of the passage of time; we experience the smoothness of the flow perhaps because of the way our cognition keeps track of time — in any case, the smoothness of the perceived flow is an issue out of the domain of physics, and probably one in the domain of cognitive science in want of an explanation. So: would you prefer one idea over another solely on the basis of Occam’s razor? The reader who brought up this objection did not think that Occam’s razor constitutes a sufficient basis. But I think it does, because Occam’s razor is not just an intellectual tool, good for philosophical discussions only, but a fundamental pillar of cognition, as I explain in this article (see the “2nd principle” in that article): a “law” that we use every moment, unknowingly, throughout our lives. In addition, Occam’s razor has worked wonders throughout the enterprise of physics; there is no reason to throw it now out the window because we are sentimentally attached to a more intuitive — even if more complex — view of the world. Back in the times of Copernicus, I imagine there were thinkers who objected to the idea that the Earth is not at the center of the world, based on purely sentimental reasons. The cognitive illusion idea similarly attacks a cherished belief: that cognition is something special in the universe (recall Freeman Dyson’s thought). But our liking or disliking should not be a reason for selecting among explanatory alternatives. |
That’s what I have in terms of feedback, so
far. Feel free to contact me and
add to this discussion, supporting your existence in some way
that I overlooked. ![]()
Σημειώσεις (κάνοντας κλικ στον αριθμό της σημείωσης μεταφέρεστε πίσω στο κείμενο):
(1) Ας σημειωθεί οτι κάθε επιφάνεια είναι από μαθηματική άποψη ένα αντικείμενο δύο διαστάσεων, ακόμα και αν καμπυλώνεται στον τριδιάστατο χώρο. Αυτό συμβαίνει γιατί τοπικά (στη “γειτονιά” κάθε σημείου) κάθε ομαλή επιφάνεια μοιάζει με ένα επίπεδο, που είναι αντικείμενο δύο διαστάσεων. Ακόμα και μια επιφάνεια με ακμές μπορεί να προσεγγιστεί από ένα σύνολο αλληλοτεμνόμενων επιπέδων.
(2) Έβαλα το πρόθεμα μακρο- εμπρός από το “διαστάσεις” γιατί κάποιες θεωρίες κβαντικής φυσικής, συμπεριλαμβανομένης και της θεωρίας των χορδών, συμπεραίνουν την ύπαρξη ενός αριθμού πρόσθετων μικροδιαστάσεων. Αυτό το γεγονός δεν θα μας απασχολήσει πάντως, γιατί εδώ εξετάζουμε τη μακροσκοπική δομή του σύμπαντος.
(3) Η αλήθεια είναι οτι υπάρχουν κάποια φυσικά συστήματα που παραβιάζουν τη συμμετρία του χρόνου, αλλά είναι μάλλον ασήμαντα. Συγκεκριμένα, υπάρχουν κάποια μάλλον εξωτικά σωματίδια, όπως τα Κ-μεσόνια και τα Β-μεσόνια, που δείχνουν οτι η λεγόμενη ασθενής πυρηνική δύναμη δεν αντιμετωπίζει το παρελθόν και το μέλλον κατά πλήρως συμμετρικό τρόπο. Εντούτοις ο Greene, όπως και άλλοι φυσικοί, πιστεύει οτι εφόσον αυτά τα σωματίδια ουσιαστικά δεν παίζουν κανένα ρόλο στον καθορισμό των ιδιοτήτων των καθημερινών υλικών σωμάτων, είναι απίθανο να παίζουν ρόλο στην εξήγηση του αινίγματος της ψυχολογικής ασυμμετρίας του χρόνου (Greene, 2004,[1] σ. 495).
(4) Ας ξεκαθαρίσουμε αυτούς τους δύο όρους: η ασυμμετρία του χρόνου αναφέρεται στην παρατήρηση οτι το παρελθόν μοιάζει διαφορετικό από το μέλλον (και το μέλλον διαφορετικό από το παρελθόν). Η κατεύθυνση του χρόνου αναφέρεται στην αίσθηση οτι η ζωή-μας μοιάζει να κινείται από το παρελθόν προς το μέλλον. Αν ο αναγνώστης δυσκολεύεται να διαχωρίσει τις δύο έννοιες, ίσως να βοηθηθεί από μια αναλογία: φανταστείτε έναν κώνο· στον κώνο υπάρχει ασυμμετρία κατά μήκος του άξονα που διατρέχει το μήκος-του, γιατί είναι στενότερος στην κορυφή και πλατύτερος στη βάση. Δεν μπορούμε όμως να εκχωρήσουμε κάποια ιδιαίτερη κατεύθυνση σ’ αυτή την ασυμμετρία, γιατί μπορούμε να διατρέξουμε τον κώνο κατά μήκος είτε από την κορυφή προς τη βάση, είτε από τη βάση προς την κορυφή. Αν αποφασίσουμε να διαλέξουμε μια συγκεκριμένη κατεύθυνση ανάμεσα στις δύο — ας πούμε, από την κορυφή προς τη βάση — τότε έχουμε προσδώσει κατεύθυνση στην ασυμμετρία του κώνου. Παρόμοια, έχουμε την εμπειρία της ύπαρξης κατεύθυνσης στο χρόνο όταν αισθανόμαστε το μέλλον να “έρχεται προς τα μας”, και το παρελθόν να “μένει πίσω”, και όχι το αντίθετο.
(5) Η εντύπωση αυτή θυμίζει την οφθαλμαπάτη της Σελήνης: όταν μετράμε τη φαινόμενη διάμετρο της Σελήνης με όργανα της φυσικής, βρίσκουμε την ίδια τιμή. Αλλά όταν κοιτάμε τη Σελήνη, μοιάζει μεγάλη όταν είναι κοντά στον ορίζοντα, και μικρή όταν είναι στο μέσον του ουρανού.
(6) Ο όρος “πλασμοειδές” (“plasmoid”) υφίσταται στη μοντέρνα φυσική, αλλά έχει πολύ τεχνικό περιεχόμενο. Σημαίνει: «ουριαίες ταχείες ροές πλάσματος με διπολικές Bz υπογραφές [...] παρατηρούμενες εντός στρωμάτων πλάσματος» (Hones, E. W., Jr., D. N. Baker et al., 1984: “Structure of the magnetotail at 220 Re”. Geophys. Res. Lett., no. 11, pp. 5-7). Άρα δεν υπάρχει κίνδυνος σύγχυσης με τη χρήση του όρου αυτού από εμάς, εφόσον εμείς τον χρησιμοποιούμε σε μη-τεχνικά συμφραζόμενα, αν και το νόημα της ρίζας της λέξης (“πλάσμα”) παραμένει αναλλοίωτο. Το νόημα της κατάληξης “-ειδές” πρέπει να γίνει κατανοητό κατ’ αναλογία, όπου η ίδια κατάληξη εμφανίζεται σε λέξεις όπως “ανθρωποειδές”, “πλανητοειδές”, κλπ.
(7) Σαν ένα άλλο παράδειγμα, απλώς και μόνο επειδή είναι φυσικώς δυνατό ένα αντικείμενο να κινείται ταχύτερα από μια σφαίρα, δεν σημαίνει οτι κάποιο είδος ζώου πρέπει να έχει εξελιχθεί ώστε να καταφέρνει κάτι τέτοιο.
(8) Το c είναι μεγάλο αντικειμενικά, όχι μόνο για ’μάς, που το μετράμε σαν πηλίκο μιας ορισμένης μονάδας μήκους διά μια ορισμένη μονάδα χρόνου, αλλά για όλους: απ’ όλες τις ταχύτητες που είναι δυνατές για αντικείμενα με μάζα, το c έχει τη μεγαλύτερη τιμή, και το μηδέν τη μικρότερη.
(9) Ένας φυσικός, κριτής μιας προηγούμενης έκδοσης του παρόντος άρθρου, είχε δυσκολία να αποδεχτεί αυτή την ιδέα, νομίζοντας πως παραβιάζει το σχετικιστικό συμπέρασμα οτι κανένα αντικείμενο με μη-μηδενική μάζα δεν μπορεί να φτάσει στην ταχύτητα του φωτός (πόσω μάλλον να την ξεπεράσει). Πιθανώς αυτός ο φυσικός δεν είχε την απαιτούμενη υπομονή για να καταλάβει αυτό το απλό σημείο. Η ιδέα είναι οτι το άθροισμα της αδρανειακής μάζας και της κινητικής ενέργειας του αντικειμένου παραμένει σταθερό, ενώ αυτό που μεταβάλλεται είναι το ποσοστό της μάζας σε σχέση με το σύνολο [μάζα+ενέργεια]. Αν μηδενίσουμε τη μάζα, η ενέργεια θα λάβει μια μέγιστη τιμή, και αν η αρχική αδρανειακή μάζα του αντικειμένου ήταν m0, τότε η μέγιστη ενέργεια E θα γίνει ίση με m0·c2. Στο σημείο εκείνο, το αντικείμενο θα έχει μάζα m = 0, και ενέργεια E, κινούμενο με ταχύτητα c. Αυτό που πρέπει να φανταστούμε είναι ένας μηχανισμός για τη μετατροπή της μάζας σε ενέργεια (μηχανισμό που τα μιτοχόνδρια στα κύτταρά μας ήδη κατέχουν). Δεν φαίνεται να υπάρχει κάποια παραβίαση της σχετικότητας. Τώρα, μπορεί να αντιτάξει κανείς οτι μια ολική μετατροπή του m0 σε E δεν είναι φυσικώς δυνατή (γιατί ο μηχανισμός ο ίδιος θα καταστρεφόταν κατά τη διαδικασία της μετατροπής), επομένως τα πλασμοειδή δεν μπορούν να υπάρχουν στην πραγματικότητα (που είναι επιχείρημα διαφορετικό από αυτό της παραβίασης της σχετικότητας). Αλλά ας θυμηθούμε οτι τα πλασμοειδή είναι υποθετικά όντα, που τα φανταστήκαμε για το σκοπό ενός πειράματος σκέψης. Η μη-ύπαρξή τους στην πραγματικότητα (και η ανικανότητα πραγμάτωσης των εξωτικών ιδιοτήτων-τους) ούτε αφαιρεί, ούτε προσθέτει κάτι σ’ αυτό το πείραμα σκέψης. Με άλλα λόγια, συμφωνώ οτι τα πλασμοειδή δεν υπάρχουν και δεν μπορούν να υπάρξουν στην πραγματικότητα· αλλά αυτό δεν έχει καμία σχέση με το σκοπό του πειράματος σκέψης, που επινοήθηκε για να μας βοηθήσει να καταλάβουμε κάποιες ιδιότητες της δικής-μας, ανθρώπινης νόησης.
(10) Οι φυσικοί των πλασμοειδών δεν θα μετράνε την ταχύτητα v = s / t, αλλά την αντίστροφή της v-1 = t / s, επειδή το s / t μπορεί να καταλήξει σε διαίρεση διά του μηδενός στην περίπτωση που το t παραμένει σταθερό και γίνεται κίνηση στο χώρο (αυτό που σ’ εμάς εμφανίζεται σαν κίνηση με την ταχύτητα του φωτός c). Υποθέτοντας οτι η διαίρεση διά μηδενός προκαλεί στα πλασμοειδή την ίδια αποστροφή που προκαλεί σ’ εμάς, το v-1 θα ήταν μια πιο φυσιολογική ποσότητα για μέτρηση στη φυσική των πλασμοειδών. Όσο πιο μεγάλο είναι το v-1, τόσο πιο πολύ η ενέργεια του πλασμοειδούς “εμποδίζεται” από του να κινηθεί στη φυσική-της ταχύτητα, δηλαδή το c.
(11) Σημειώστε οτι η ενέργεια ενός πλασμοειδούς δεν απειρίζεται. Εδώ δεν μιλάμε για αντικείμενα με αναλλοίωτη μάζα που φτάνουν στην ταχύτητα του φωτός (στην οποία περίπτωση η ενέργειά τους γίνεται άπειρη), αλλά για οντότητες που μπορούν να ρυθμίζουν το ποσό της μάζας που περιλαμβάνουν, έτσι ώστε η συνολική-τους ποσότητα μάζας + ενέργειας να παραμένει σταθερή.
(12) Ο αναγνώστης μπορεί να νομίσει οτι μια τέτοια ιδέα στερείται νοήματος, καθώς στην κοινή εμπειρία η “κίνηση” συνεπάγεται αλλαγή η οποία συμβαίνει εντός κάποιου χρόνου. Αλλά πρέπει να γίνει κατανοητό οτι στο παρόν κείμενο χρησιμοποιείται μια γενικευμένη έννοια “κίνησης”, με την οποία δεν εννοούμε τίποτα περισσότερο από μια ακολουθία χωροχρονικών συντεταγμένων, οι οποίες αποτελούν ένα (είτε διακριτό είτε συνεχές) σύνολο. Η αμέσως επόμενη παράγραφος στο κείμενο εξηγεί αυτή την ιδέα περαιτέρω.
(13) Ο Έλληνας φιλόσοφος Ἡράκλειτος έζησε γύρω στο 500 π.Χ., στην πόλη της Εφέσου, στη Μικρά Ασία. Το διάσημο ρητό που αποδίδεται στον Ηράκλειτο είναι: «τὰ πάντα ῥεῖ, καὶ οὐθὲν μένει» («όλα αλλάζουν, και τίποτε δεν μένει το ίδιο»).
(14) Η παγίδα είναι, όπως μαθαίνουμε στα μαθηματικά των άπειρων σειρών (που
ήσαν άγνωστα την εποχή του Ζήνωνα), οτι το άθροισμα μιας άπειρης ακολουθίας
αριθμών μπορεί να είναι πεπερασμένος αριθμός. Έτσι, παρόλο που το μήκος του
διαστήματος που διανύουν ο Αχιλλέας και η χελώνα μπορεί να διαιρεθεί σε άπειρο
αριθμό μικρότερων διαστημάτων, αν αθροίσουμε εκείνα τα μικρότερα διαστήματα θα
λάβουμε ως άθροισμα ένα πεπερασμένο συνολικό μήκος, και άρα ο Αχιλλέας θα
συναντήσει τη χελώνα εντός ενός πεπερασμένου χρόνου (και αμέσως μετά θα την
προσπεράσει).
Ο αναγνώστης μερικές φορές εξακολουθεί να απορρίπτει αυτή την εξήγηση
επιχειρηματολογώντας ως εξής: ας υποθέσουμε οτι ο Αχιλλέας φτάνει στο πρώτο
σημείο των 100 m σε 10 δευτερόλεπτα, οπότε παίρνουμε
μια φωτογραφία εκείνη τη στιγμή. Στο επόμενο σημείο, που είναι τα 101
m, παίρνουμε μια δεύτερη φωτογραφία, που συμβαίνει στα
10,01 δευτερόλεπτα. Την επόμενη (τρίτη) φωτογραφία την παίρνουμε στα 10,0101
δευτερόλεπτα, και ούτω καθεξής, επ’ άπειρο. Αλλά εφόσον πάντα θα μπορούμε
να παίρνουμε φωτογραφίες, η διαδικασία της λήψης φωτογραφιών δεν θα τελειώσει
ποτέ, άρα ο Αχιλλέας δεν θα κινηθεί ποτέ λίγο παραπάνω από τα 100
m.
Αυτή η συλλογιστική, αν και ακούγεται λογική από μαθηματική άποψη, αποτυγχάνει
από φυσική άποψη για δύο λόγους. Πρώτον, δεν είναι σωστό οτι μπορούμε να
παίρνουμε φωτογραφίες επ’ άπειρο, γιατί καθώς τα χρονικά διαστήματα γίνονται όλο
και συντομότερα, σε κάποιο σημείο να είναι αδύνατο για τα φωτόνια του φωτός να
διανύσουν την απόσταση μεταξύ δρομέα και κάμερας, οπότε καμιά φωτογραφία δεν
μπορεί να ληφθεί πέρα από εκείνο το χρονικό σημείο. Και το δεύτερο πρόβλημα
είναι οτι αυτή η ιδέα θεωρεί οτι ο χρόνος είναι διαιρετός επ’ άπειρο, που μάλλον
δεν είναι σωστό (ο χρόνος μάλλον είναι διακριτός).
Παραπομπές (πατώντας στον αριθμό της παραπομπής μεταφέρεστε στο σημείο του κειμένου όπου αναφέρεται η παραπομπή για πρώτη φορά):
[1] Greene, Brian R. (2004). The fabric of the cosmos: space, time, and the texture of reality. New York: Knopf.
[2] Einstein, Albert. (1905). “On the electrodynamics of moving bodies”. Annalen der Physik, vol. 17, pp. 891-921.
[3] Dickson, W. Michael (1998). Quantum Chance and Non-Locality: Cambridge University Press.
Back to Harry’s index of topics in philosophy