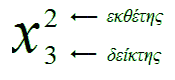 |
Νους – ΈννοιεςΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ Ν2 ΤΟΥ Δ.Ε.Π.
|
Στόχος του μαθήματος και η κεντρική υπόθεση της νοολογίας
Στο παρόν μάθημα (Ν2) εξετάζεται ο νους από υψηλό επίπεδο, αντίθετα από το μάθημα Ν3 που εξετάζει τον εγκέφαλο, που είναι το όργανο μέσω του οποίου προκύπτει ο νους σαν αναφυόμενη ιδιότητα (αγγλ.: emergent property). Πάντως, στη νοολογία δεν θεωρείται δεδομένο το οτι ένας νους υποχρεωτικά προκύπτει από τον ανθρώπινο εγκέφαλο και μόνο. Εξετάζοντας τις ιδιότητες και τη δόμηση του νου σε αφηρημένο επίπεδο (δηλαδή χωρίς να ενδιαφερόμαστε ιδιαίτερα για το πώς υλοποιούνται οι ιδιότητες αυτές μέσω των εγκεφαλικών νευρώνων) βλέπουμε οτι ίσως στο μέλλον γίνει δυνατό να υλοποιηθεί ένας νους (με όλες τις ανθρώπινές του ιδιότητες) και μέσω υπολογιστών. Το οτι αυτό δεν έχει γίνει μέχρι σήμερα οφείλεται μάλλον στο οτι δεν έχουμε κατανοήσει πλήρως την αρχιτεκτονική του νου, και όχι στο οτι υπάρχει κάποιο υποτιθέμενο ανυπέρβλητο εμπόδιο που απαγορεύει την υλοποίηση ενός νου μέσω κάποιου άλλου υλικού συστήματος εκτός του εγκεφάλου. Παρόλο που η γνώση-μας δεν είναι πλήρης, το μάθημα Ν2 εξετάζει τα όσα γνωρίζουμε μέχρι σήμερα στον τομέα αυτόν.
Η κεντρική υπόθεση της νοολογίας που εξετάζεται στο παρόν μάθημα είναι η εξής:
-
όπως ένα κομμάτι ύλης αποτελείται από μόρια,
-
όπως ένα έμβιο ον αποτελείται από κύτταρα,
-
όπως ένας εγκέφαλος αποτελείται από νευρώνες,
-
έτσι και ένας νους αποτελείται από έννοιες (αγγλ.: concepts).
Σε κάθε περίπτωση έχουμε ένα “πολύπλοκο σύστημα” (αγγλ.: complex system, ήτοι: κομμάτι ύλης, έμβιο ον, εγκέφαλος, νους), το οποίο αποτελείται από δομικά υλικά, που παρουσιάζουν μια ομοιομορφία μεταξύ-τους και κοινές ιδιότητες. Π.χ. η ομοιομορφία των κυττάρων συνίσταται στο οτι έχουν μια εξωτερική μεμβράνη, οργανίδια, DNA, πιθανώς πυρήνα, και άλλα κοινά χαρακτηριστικά· γιαυτό άλλωστε μπορούμε και εξετάζουμε “το κύτταρο” σαν μια οντότητα στη βιολογία (μάθημα Β4). Τα δομικά υλικά ενός νου είναι οι έννοιες, των οποίων τις κοινές ιδιότητες και δομή εξετάζει το παρόν μάθημα.
Υπάρχει όμως μια διαφορά μεταξύ των παραπάνω τριών πρώτων παραδειγμάτων πολύπλοκων συστημάτων (κομμάτι ύλης, έμβιο ον, εγκέφαλος) και του νου: η διαφορά είναι οτι τα πρώτα τρία είναι υλικά με την άμεση έννοια, δηλαδή είναι απτά, ορατά, και γενικά αντιληπτά μέσω των αισθήσεων· ενώ αντίθετα, ένας νους δεν είναι εύκολο να πούμε οτι είναι “υλικός” με την άμεση έννοια — τουλάχιστον δεν γίνεται αντιληπτός μέσω των αισθήσεων: δεν τον βλέπουμε, ούτε τον ακούμε, μυρίζουμε, γευόμαστε, ή ακουμπάμε. Αυτό όμως δεν σημαίνει οτι ο νους δεν υπόκειται στους νόμους της φύσης.(*) Οι φυσικοί νόμοι στους οποίους υπόκειται ο κάθε νους (ανεξάρτητα από τη θέληση ή την ευφυΐα του ανθρώπου που τον κατέχει) εξετάζονται επίσης στο παρόν μάθημα. Πρέπει όμως να τονιστεί οτι οι νόμοι αυτοί, ενώ είναι νόμοι φυσικοί, δεν ανήκουν στον τομέα της φυσικής καθαυτό, για τον ίδιο λόγο που οι νόμοι π.χ. της λειτουργίας των έμβιων όντων δεν εξετάζονται από τη φυσική, αλλά από τη βιολογία. Παρόμοια, οι νόμοι που διέπουν τη λειτουργία ενός νου εξετάζονται από τη νοολογία.
Η έννοια της έννοιας
Τί εννοούμε με τη λέξη “έννοια”; Η έννοια της έννοιας είναι μία από εκείνες τις οντότητες που δυσκολευόμαστε να τη βάλουμε σε καλούπια. Διαισθητικά θεωρούμε οτι ξέρουμε τί σημαίνει η λέξη — αλλιώς δεν θα την είχαμε στη γλώσσα-μας — αλλά όταν μας ζητούν να ορίσουμε τον όρο “έννοια”, συνήθως μένουμε αμήχανοι.
Μια πρώτη — και όχι πολύ πετυχημένη — προσπάθεια θα ήταν να πούμε οτι έννοιες είναι, πάνω-κάτω, αυτά τα πράγματα για τα οποία έχουμε στη γλώσσα-μας μια “λέξη με περιεχόμενο”, με νόημα· δηλαδή λέξη που να είναι είτε ουσιαστικό, είτε ρήμα, είτε επίθετο, είτε επίρρημα. Παράδειγμα: το “σπίτι”, σαν ουσιαστικό, είναι μια έννοια. Το ίδιο και η “δημοκρατία”, που είναι αφηρημένο ουσιαστικό. Το “τρέχω”, σαν ρήμα, είναι έννοια· το ίδιο και το “θυμάμαι”, που είναι κάπως πιο αφηρημένο από το “τρέχω”, καθώς μπορούμε εύκολα να ζωγραφίσουμε έναν άνθρωπο που τρέχει, αλλά όχι και τόσο εύκολα (ή πειστικά) έναν άνθρωπο που θυμάται. Τα επίθετα, είτε συγκεκριμένα όπως το “κόκκινο”, είτε πιο αφηρημένα όπως το “άριστο”, είναι επίσης έννοιες. Το ίδιο μπορούμε να πούμε και για τα επιρρήματα, όπως το “γρήγορα” (π.χ. “τρέχω γρήγορα”), ή το “εύκολα” (π.χ. “θυμάμαι εύκολα”). Παρατηρούμε λοιπόν οτι μια έννοια μπορεί να είναι πιο συγκεκριμένη, ή πιο αφηρημένη ως ένα βαθμό. Αυτό ας το κρατήσουμε σαν ιδέα, γιατί θα φανεί σημαντικό σε μετέπειτα στάδια του παρόντος μαθήματος.
Η παραπάνω προσπάθεια είναι απλώς “μια καλή αρχή”, αλλά έχει προβλήματα. Π.χ. η γλώσσα έχει και άλλου τύπου λέξεις. Λέξη είναι και το “και” — είναι το “και” έννοια; Θα μπορούσε κανείς να πει οτι είναι: πρόκειται για την έννοια της σύνδεσης (ή σύζευξης) άλλων εννοιών, γιαυτό και λέγεται “συζευκτικός σύνδεσμος”. Όμως τί κάνουμε με τα άρθρα “η”, “τους”, ή το μόριο “να”; Ή με τον ειδικό σύνδεσμο “οτι” (που λέγεται “ειδικός” γιατί δεν ξέρουμε πώς να τον πούμε, επειδή δεν αντιστοιχεί σε καμία έννοια); Άρα δεν αντιστοιχούν όλες οι λέξεις σε έννοιες. Έπειτα — το αντίστροφο — υπάρχουν και έννοιες για τις οποίες δεν έχουμε λέξεις. Πώς θα πείτε, λόγου χάρη, με ένα ουσιαστικό, την κατάσταση κατά την οποία αισθάνεστε άβολα; (Προσπαθείστε να βρείτε όχι απλώς ένα παράδειγμα με μια τέτοια κατάσταση, αλλά λέξη που να περιγράφει κάθε τέτοια κατάσταση όπου αισθανόμαστε άβολα.) Στα αγγλικά υπάρχει η λέξη “inconvenience”. Η γλώσσα-μας μοιάζει να μην έχει λέξη για την έννοια αυτή. Αλλά αυτό δεν σημαίνει οτι τα αγγλικά είναι “πιο πλήρης” γλώσσα, γιατί στα ελληνικά έχουμε το κοινότατο ρήμα “διώχνω”, μια έννοια για την οποία δεν υπάρχει λέξη στα αγγλικά. (Ο ομιλητής της αγγλικής μπορεί να εκφράσει περιφραστικά την έννοια αυτή με το: “I force someone to leave”.) Άλλο παράδειγμα είναι οτι στα ελληνικά μία λέξη, το “χέρι”, σημαίνει δυό διαφορετικές έννοιες: τόσο ολόκληρο το άκρο από τον ώμο και κάτω, όσο και το μέρος από τον καρπό μέχρι τα δάχτυλα. Οι περισσότερες άλλες γλώσσες του κόσμου κάνουν διάκριση (π.χ. αγγλ.: arm – hand)· το ίδιο ισχύει και για το “πόδι” (αγγλ.: leg – foot). Ή, ας σκεφτούμε το εξής: με ποια λέξη να περιγράψουμε κάποιον χαρακτηριστικό τύπο Έλληνα ή Ελληνίδας που τον βλέπουμε σε διάφορες παραλλαγές στο δρόμο σχεδόν κάθε μέρα; Μόλις δούμε άλλο ένα παράδειγμα αυτού του τύπου προσώπου, μας έρχεται στο νου η έννοια “Έλληνας”, αλλά βέβαια αυτή δεν είναι η λέξη για την έννοια, γιατί υπάρχουν πολλοί άλλοι τύποι Ελλήνων. Αυτός ο τύπος όμως είναι τόσο χαρακτηριστικός, που και στο εξωτερικό να τον βλέπαμε θα σκεφτόμασταν αμέσως: «Αυτός/αυτή πρέπει να είναι Έλληνας/Ελληνίδα!» Βλέπουμε λοιπόν οτι δεν υπάρχει μια ένα-προς-ένα αντιστοιχία μεταξύ εννοιών και λέξεων. Άρα οι λέξεις δεν μας λένε ακριβώς ποιες είναι οι έννοιες που έχουμε στο νου-μας.
Το τί είναι μια έννοια έχει απασχολήσει τον άνθρωπο από την αρχαιότητα. Όπως και με τόσες άλλες έννοιες, έτσι και με την έννοια της έννοιας, μπορούμε να βρούμε τις ρίζες-της στη διανόηση της ελληνικής αρχαιότητας. Είναι χρήσιμο να κάνουμε μια ιστορική αναδρομή σ’ αυτήν την προσπάθεια, γιατί θα μάθουμε τόσο το πού οι Έλληνες φιλόσοφοι προσέγγισαν σωστά το θέμα, όσο και το πού έκαναν λάθος — ώστε να μην επαναλάβουμε το λάθος σήμερα. Τουλάχιστον θα μάθουμε οτι είναι λάθος να ζητάμε έναν ορισμό της έννοιας “έννοια”, και θα καταλάβουμε το γιατί είναι λάθος.
Πλάτωνας, και η κλασική θεωρία της έννοιας
Οι αρχαίοι Έλληνες φιλόσοφοι δεν μιλούσαν για έννοιες, αλλά για είδη, ή κατηγορίες, όπως θα τις λέγαμε σήμερα. Π.χ., το σύνολο όλων των αλόγων είναι ένα είδος: πρόκειται για την κατηγορία αντικειμένων που περιλαμβάνει όλα τα άλογα, η οποία είναι προφανώς διαφορετικό αντικείμενο από την Αστραπή, ένα συγκεκριμένο άλογο. Όπως θα δούμε, η έννοια “κατηγορία” ταυτίζεται με την έννοια “έννοια”, από νοολογική άποψη. Επομένως οι εξερευνήσεις των Πλάτωνα και Αριστοτέλη αποτελούν την πρώτη θεωρία νοολογίας που υπήρξε ποτέ. Ας δούμε τί περιλάμβανε εκείνη η θεωρία.
 |
Κατά τον Πλάτωνα, ο κόσμος χωρίζεται σε δύο οντότητες: στα καθημερινά, ατελή αντικείμενα, που γίνονται αντιληπτά από τις αισθήσεις, και στο σύνολο των ιδεών, που είναι απαλλαγμένες από τις ατέλειες των αισθητών αντικειμένων. Παράδειγμα: η Νίκη, ο Θωμάς, ο Λευτέρης, η Γεωργία, είναι συγκεκριμένα άτομα. Το καθένα υποχρεωτικά έχει κάποιες ατέλειες, είτε στο σώμα, είτε στο χαρακτήρα. Όμως η ιδέα (ή κατηγορία, ή έννοια) άνθρωπος είναι απαλλαγμένη από τις ατέλειες αυτών των ατόμων. Σύμφωνα με τη θεωρία των Ιδεών, του Πλάτωνα, υπάρχει ένας κόσμος τέλειων Ιδεών, που είναι ξεχωριστός από τον κόσμο των αισθήσεων. Οι Ιδέες δηλαδή, κατά τον Πλάτωνα, δεν βρίσκονται απλώς στα κεφάλια των ανθρώπων, αλλά αποτελεούν έναν ξεχωριστό (αλλά φυσικό) κόσμο, ένα “παράλληλο σύμπαν” όπως θα λέγαμε σε σημερινή ορολογία. |
Μπορεί η δυϊστική άποψη οτι υπάρχει ένας φυσικός κόσμος Ιδεών παράλληλος με αυτόν που αντιλαμβανόμαστε να μη στέκει σήμερα σε σοβαρή επιστημονική εξέταση. Όμως η ιδέα οτι αφαιρώντας τις ατέλειες των καθημερινών αντικειμένων καταλήγουμε σε ένα “τέλειο”, ιδεατό αντικείμενο, αποτελεί την πρώτη — και συνάμα βαθύτατη — ιδέα μιας νοολογικής θεωρίας που ξεκίνησε τότε, 24 αιώνες πριν. Ας εξετάσουμε πιο προσεκτικά την ιδέα αυτή. Έστω οτι μας δίνονται τα ακόλουθα τρίγωνα:

Κανένα από τα παραπάνω τρίγωνα δεν είναι ίδιο με κάποιο άλλο. Όλα είναι φτιαγμένα με το χέρι, και οπωσδήποτε το καθένα έχει αρκετές ατέλειες. Ας φανταστούμε τώρα χιλιάδες τέτοια τρίγωνα, και ας τα τοποθετήσουμε το ένα πάνω στ’ άλλο, έτσι ώστε σε όσο πιο πολλά σημεία οθόνης (pixels) συμπίπτουν, τόσο πιο μαύρη να είναι η μελάνη, ενώ όσα σημεία καλύπτονται από λιγότερα τρίγωνα (δηλαδή από τις μαύρες πλευρές-τους, όχι το εσωτερικό-τους), τα σημεία αυτά να είναι πιο γκρίζα — τόσο πιο ανοιχτά γκρίζα όσο πιο λίγα τα τρίγωνα που καλύπτουν τα σημεία εκείνα. Θα πάρουμε τότε κάτι σαν αυτό που απεικονίζεται παρακάτω:
Το παραπάνω τρίγωνο λέγεται πρότυπο (αγγλ.: prototype), και προέκυψε από τα συγκεκριμένα, τα ατελή τρίγωνα. Βλέπουμε οτι από το πρότυπο έχουν αφαιρεθεί οι ατέλειες. Αυτή η αφαίρεση δεν έγινε με το χέρι, αλλά με μια μηχανική διαδικασία: τοποθετώντας τα τρίγωνα το ένα πάνω στ’ άλλο. Μπορούμε μάλιστα να συνεχίσουμε την αφαιρετική διαδικασία με άλλο τρόπο: να πάρουμε το παραπάνω πρότυπο και ν’ αρχίσουμε να αφαιρούμε τα πιο αχνά γκρίζα σημεία· στη συνέχεια τα κάπως πιο έντονα γκρίζα, μετά τα ακόμα πιο έντονα, κ.ο.κ., ώσπου να μείνουν μόνο τα εντελώς μαύρα σημεία. Αυτά θα πρέπει να βρίσκονται κάπου στο μέσον, στο “σκελετό” των τριών γραμμών. Έτσι θα πάρουμε την παρακάτω εικόνα:
Το τρίγωνο στα δεξιά είναι τόσο λεπτό που μπορούμε να το φανταστούμε με ακόμα πιο αφηρημένο τρόπο: σαν οι γραμμές-του να μην έχουν καθόλου πάχος, σαν να αποτελούνται μόνο από μήκος. Έτσι φτάνουμε στη γεωμετρική, αφηρημένη έννοια του τριγώνου. Μάλιστα, αυτό θα είναι μεν αφηρημένο τρίγωνο αλλά με συγκεκριμένα μήκη πλευρών και συγκεκριμένες γωνίες. Όμως θεωρώντας πολλά τέτοια αφηρημένα τρίγωνα, και κρατώντας μόνο ότι έχουν κοινό (δηλαδή τις τρεις πλευρές και τρεις κορυφές), φτάνουμε στην “Πλατωνική ιδέα” του τριγώνου, στην έννοια “τρίγωνο”, που είναι αντικείμενο μελέτης της γεωμετρίας (την οποία ο Πλάτωνας θεωρούσε απαραίτητο εφόδιο του νου: «μηδείς αγεωμέτρητος εισίτω» έγραφε πάνω από την είσοδο στην Ακαδημία-του).
Βέβαια ο Πλάτωνας δεν περιέγραψε τον παραπάνω αλγόριθμο, δηλαδή τη μηχανική διαδικασία μέσω της οποίας φτάσαμε από τα συγκεκριμένα και ατελή στο αφηρημένο και τέλειο. Αλλά αν ζούσε στη σημερινή εποχή των υπολογιστών και των αλγορίθμων, ίσως να συμφωνούσε οτι με τον παραπάνω αλγόριθμο ξεκινάμε από το ορατό και οδηγούμαστε στο ιδεατό, σε μια από τις “Ιδέες”-του. Ακόμα πιο σημαντικό για το θέμα-μας είναι οτι τον αλγόριθμο αυτό μπορεί να τον εκτελέσει και ένας υπολογιστής — δεν απαιτείται ανθρώπινη ευφυΐα. Αργότερα θα ξανασυναντήσουμε αυτήν τη σημαντική “μέθοδο παραγωγής ιδεών από ατελή αντικείμενα”.
Η άλλη σημαντική συνεισφορά του Πλάτωνα σε μια “θεωρία νοολογίας” είναι η ιδέα οτι για κάθε είδος (διάβαζε: έννοια) μπορεί να δοθεί ένας ορισμός που να το ξεχωρίζει από τα άλλα είδη. Π.χ. ένας ελέφαντας είναι το παχύδερμο εκείνο που διαθέτει προβοσκίδα· ο άνθρωπος είναι «κάθε δίποδο άπτερο»· κ.ο.κ. (Ο Πλάτωνας βέβαια δεν γνώριζε τα καγκουρό.) Κάθε είδος ανήκει σε μια μεγαλύτερη κατηγορία, το γένος, και έχει μια “ειδοποιό διαφορά” που το ξεχωρίζει από τα άλλα είδη του ίδιου γένους. (Από εδώ προέκυψε η σύγχρονη πρακτική ταξινόμησης των έμβιων όντων στη βιολογία σε “γένος – είδος”.)
Ο Αριστοτέλης και η αναλυτική θεωρία της έννοιας
Την ιδέα οτι για κάθε είδος μπορεί να δοθεί ένας ορισμός την ασπάστηκε κι ο μαθητής του Πλάτωνα, Αριστοτέλης, ο οποίος μάλιστα απέδωσε την πατρότητά της στο Σωκράτη, και εισήγαγε την ιδέα οτι ο ορισμός δίνεται μέσω μιας αναγκαίας και ικανής συνθήκης. Μέσω του Αριστοτέλη, η ιδέα αυτή έγινε ένα από τα “πολιτισμικά θεμέλια” του Δυτικού τρόπου σκέψης. Πολύ συχνά σήμερα, όταν δύο άτομα συζητούν για κάτι, ακούμε τον ένα να λέει: «Πώς το ορίζεις αυτό, ποιος είναι ο ορισμός-του;» Ζητάμε να γνωρίζουμε με ακρίβεια “για τί πράγμα μιλάμε”, επομένως να μπορούμε να δώσουμε έναν ορισμό για κάθε έννοια της οποίας κάνουμε χρήση. Γιαυτό κάποτε οι συζητητές ανατρέχουν σε λεξικά, εγκυκλοπαίδειες, κλπ, προσπαθώντας να εντοπίσουν τον ορισμό μιας υπό συζήτηση έννοιας. Όπως προαναφέρθηκε όμως, η ιδέα οτι το κάθε είδος (έννοια) ορίζεται με αυστηρό τρόπο στο νου του ανθρώπου δεν είναι σωστή, γιατί — όπως θα δούμε — έρχεται σε σύγκρουση με την παρατήρηση και το πείραμα.
 |
Ο Αριστοτέλης, εκτός του οτι συμφώνησε με την ιδέα της ύπαρξης ορισμού για κάθε έννοια, πρότεινε και μια αναλυτική θεωρία του νου που έχει ένα σπουδαίο κοινό χαρακτηριστικό με σύγχρονες παρόμοιες απόπειρες. Συγκεκριμένα, ο Αριστοτέλης θεώρησε οτι υπάρχουν ορισμένα πρωταρχικά και απλά στοιχεία, μέσω των οποίων συνθέτονται όλες οι έννοιες. Πριν να δούμε ποια είναι τα πρωταρχικά, απλά στοιχεία που συνθέτουν τις έννοιες, ας σημειώσουμε οτι αυτή η ιδέα (δηλαδή της αναγωγής του σύνθετου σε ένα σύνολο απλών στοιχείων) είναι μια ιδέα που κυριάρχησε στη Δυτική σκέψη, και ξεκίνησε από τους αρχαίους Έλληνες διανοητές. Ο Θαλής, λόγου χάρη, ανήγαγε όλη την πολυπλοκότητα της φύσης σε ένα στοιχείο: το νερό. Ο Ηράκλειτος πρότεινε σαν τέτοιο στοιχείο το πυρ. Νωρίτερα, ο Πυθαγόρας είχε προτείνει κάτι πιο αφηρημένο: τους αριθμούς (και ίσως να ήταν τελικά εκείνος που πέτυχε “διάνα”). Στη συνέχεια ο Δημόκριτος πρότεινε τα άτομα, μια άποψη που βρήκε τη δικαίωσή της από τον 18o αιώνα μέχρι τις αρχές του 20ού (βλ. Ιστορία της επιστήμης (Ε2), σύγχρονη ατομική θεωρία). |
Η αναλυτική σκέψη επεκτάθηκε αργότερα στην αναγωγή των γαλαξιών σε σύνολα αστέρων· στην αναγωγή των έμβιων όντων σε σύνολα κυττάρων· στην αναγωγή των εγκεφάλων σε σύνολα νευρικών κυττάρων (νευρώνων)· και, όπως πρόκειται να συζητήσουμε στο παρόν μάθημα, στην αναγωγή του νου σε σύνολο εννοιών. Αλλά ας δούμε τα “νοητικά στοιχεία” του Αριστοτέλη, τα οποία δίνονται συνοπτικά στον παρακάτω πίνακα:
| Στοιχειώδης Κατηγορία (νοητικό στοιχείο) |
Περιγραφή | Παράδειγμα του Αριστοτέλη | ||||||||||||
|
|
|
||||||||||||
| Ποσότητα (ποσόν) | πόσο μεγάλο/μικρό, πόσο πολύ/λίγο | τετράποδο, πεντάποδο | ||||||||||||
| Ποιότητα (ποιόν) | τί είδους πράγμα | άσπρο, εγγράμματο | ||||||||||||
| Σχέση (πρὸς τί) | συγκρινόμενο με κάτι άλλο | διπλό, μισό, μεγαλύτερο | ||||||||||||
| Τοποθεσία (ποῦ) | σε ποια θέση στο χώρο | στο Λύκειο, στην αγορά | ||||||||||||
| Χρόνος (πότε) | σε ποια χρονική στιγμή | χθες, πέρισυ | ||||||||||||
| Θέση (κεῖσθαι) | ευρισκόμενο | βρίσκεται, κείται | ||||||||||||
| Κατάσταση (ἔχειν) | σε τί κατάσταση είναι | ντυμένο, οπλισμένο | ||||||||||||
| Δράση (ποιεῖν) | τί κάνει (ενεργά) | κόβει, καίει | ||||||||||||
| Διεργασία (πάσχειν) | τί του κάνουν, ή τί πάσχει (παθητικά) | κόβεται, καίγεται |
Η κάθε έννοια, κατά τον Αριστοτέλη, αποτελείται από κάποια από τα παραπάνω “συστατικά”. Όπως π.χ. το νερό αποτελείται από δύο συστατικά στοιχεία, το υδρογόνο και το οξυγόνο (καθώς βέβαια έγινε γνωστό πολύ αργότερα), έτσι και μια έννοια όπως το “φως” αποτελείται από κάποια νοητικά στοιχεία, όπως μια Ουσία (πιθανώς μια φωτεινή ουσία, όπως θα την εννοούσαν οι αρχαίοι Έλληνες), μια Ποιότητα (είναι φωτεινό/λαμπρό), μια Δράση (φωτίζει/ζεσταίνει), κλπ. Τα νοητικά στοιχεία δεν αναλύονται περαιτέρω — γιαυτό άλλωστε τα λέμε “στοιχεία”.
Σαν ιδέα, η θεωρία του Αριστοτέλη είναι ενδιαφέρουσα, γιατί εμπεριέχει τον σπόρο της σημερινής αντίληψης οτι όντως υπάρχουν κάποια νοητικά στοιχεία από τα οποία “χτίζονται” οι πιο σύνθετες έννοιες. Σήμερα όμως αντιλαμβανόμαστε οτι τα νοητικά στοιχεία δεν μπορεί να είναι τόσα λίγα όσα παρέθεσε ο Αριστοτέλης. Επίσης, μια έννοια δεν είναι απλώς μια λίστα από τα νοητικά στοιχεία που περιέχει· τα στοιχεία αυτά συνδέονται μεταξύ-τους με διάφορους τρόπους (το πώς εξετάζεται στο μάθημα Ν5), δομώντας την έννοια με συγκεκριμένο τρόπο. Κατ’ αναλογία, το μόριο του νερού δεν είναι απλώς “υδρογόνο και οξυγόνο”· είναι μια δομή ενός ατόμου οξυγόνου και δύο ατόμων υδρογόνου, τοποθετημένα έτσι ώστε το οξυγόνο να είναι στην κορυφή μιας γωνίας 105°. Παρόμοιες δομές (αλλά όχι γεωμετρικής φύσης) σχηματίζουν τα νοητικά στοιχεία που αποτελούν τις έννοιες, όπως μαθαίνουμε στο μάθημα Ν5.
Κριτική της κλασικής θεωρίας περί ορισμών
Η Πλατωνική–Αριστοτέλεια αντίληψη περί εννοιών που διαφοροποιούνται μέσω μιας “ειδοποιού διαφοράς”, και που είναι επιδεκτικές ορισμών, επικράτησε επί σχεδόν δυόμισι χιλιετίες γιατί δεν είχε εντωμεταξύ προταθεί τίποτε καλύτερο. Κατά το τελευταίο τέταρτο του 20ού αιώνα όμως άρχισαν να συσσωρεύονται οι πειραματικές ενδείξεις οτι σχεδόν όλες οι κοινές έννοιες (πλην εκείνων που συναντούμε στα μαθηματικά) δεν είναι αυστηρά ορισμένες στο νου των ανθρώπων.
Από επιστημονική άποψη, αυτό που πρέπει να μας απασχολεί είναι όχι το πώς θα έπρεπε να ορίζονται οι έννοιες, αλλά το αν όντως δουλεύουμε μέσω ορισμών μέσα στα κεφάλια-μας. Όταν π.χ. σκέφτομαι “άλογο”, λειτουργώ μέσω ενός ορισμού αυτής της έννοιας; Το αν υπάρχει ή όχι καλός ορισμός της έννοιας “άλογο” είναι άλλο ερώτημα. (Μπορεί και να υπάρχει· π.χ. μέσω αναφοράς στο DNA του σημερινού τυπικού αλόγου.) Όμως όταν σκεφτόμαστε, σκεφτόμαστε μέσω ορισμών;
Ερευνητές της γνωσιακής ψυχολογίας άρχισαν να εξετάζουν το πώς αντιλαμβάνονται οι άνθρωποι τις διάφορες έννοιες από τα τέλη της δεκαετίας του ’70. Σε μια από τις έρευνες, ο Τζ. Α. Χάμπτον (J. A. Hampton) ζήτησε από τους εξεταζόμενους (τα “υποκείμενα”, σε όρους εργαστηριακής ψυχολογίας) να κατατάξουν διάφορα ουσιαστικά σαν “λαχανικά” ή “μη λαχανικά”. Έτσι βρήκε οτι τα υποκείμενα κατέτασσαν τις ντομάτες μόλις εκτός λαχανικών (σε ορισμένες κοινωνίες, η ντομάτα θεωρείται κάτι μεταξύ λαχανικού και φρούτου), ενώ τα φύκια μόλις εντός των λαχανικών (σε μερικές κουλτούρες, π.χ. στην Ιαπωνική, κάποια φύκια είναι συνοδευτικά του κυρίως γεύματος). Το “μόλις” (εντός ή εκτός) είναι αποτέλεσμα στατιστικής μέσης τιμής, και σημαίνει οτι άλλα υποκείμενα τοποθετούσαν τις ντομάτες ή τα φύκια εντός της κατηγορίας, και άλλα εκτός, δηλαδή δεν συμφωνούσαν μεταξύ-τους. Άρα αν έχουμε έναν εσωτερικό ορισμό για την έννοια “λαχανικό”, πώς εξηγείται η σχεδόν πλήρης ασυμφωνία μεταξύ των ανθρώπων για ορισμένα είδη; Θα μπορούσε να ισχυριστεί κανείς οτι μπορεί μεν να διαφωνούν οι άνθρωποι μεταξύ-τους, ίσως γιατί έχουν διαφορετικούς ορισμούς, αλλά κάθε συγκεκριμένο άτομο πρέπει να είναι συνεπές, γιατί χρησιμοποιεί τον ίδιο ορισμό. Όμως πειράματα που έγιναν από τους Μακλόσκυ (McCloskey) και Γκλάξμπεργκ (Glucksberg) το 1978 έδειξαν οτι το ίδιο το υποκείμενο διαφωνεί με τον εαυτό-του! Δηλαδή, όταν ζητούσαν από το υποκείμενο να επαναλάβει το πείραμα μετά από μερικές εβδομάδες, τότε τοποθετούσε τα είδη σε διαφορετικές κατηγορίες, έχοντας ξεχάσει πώς τα είχε κατατάξει πρωτύτερα.
Το θέμα δεν αφορά μόνο σε “μερικά λαχανικά”, όπως ντομάτες και φύκια. Έγιναν πάμπολλα πειράματα με διαφορετικές κατηγορίες, και βρέθηκε οτι σε κάθε κατηγορία υπάρχουν κάποια είδη που είναι πιο τυπικά από άλλα, και είδη που βρίσκονται πιο κοντά στο όριο του “είναι και δεν είναι μέλος” της κατηγορίας. Για παράδειγμα, στην κατηγορία “πτηνό”, το σπουργίτι είναι τυπικό μέλος, έχοντας όλα τα χαρακτηριστικά που τυπικά αποδίδουμε σε πτηνά. (Ενδιαφέρον είναι το οτι όταν εξετάζονται Αμερικανοί, βρίσκουν οτι πιο τυπικό πτηνό είναι ο κοκκινολαίμης [robin], γιατί σε πολλές Πολιτείες αυτό είναι πιο κοινό πουλί από το σπουργίτι.) Όμως μια κότα είναι — σύμφωνα πάντα με τις ενδείξεις των υποκειμένων — λιγότερο τυπικό πτηνό, αφού δεν πετάει· και σίγουρα ακόμη “λιγότερο πτηνά” είναι η στρουθοκάμηλος και ο πιγκουΐνος. Υπόψη οτι αυτά τα ευρήματα δεν γίνονται ρωτώντας τα υποκείμενα κατευθείαν την ερώτηση “Πείτε-μας πόσο τυπικά πτηνά είναι τα παρακάτω”, αλλά έμμεσα, βλέποντας πόσο γρήγορες είναι οι αποκρίσεις των υποκειμένων στην έννοια “πτηνό” όταν το ερέθισμα είναι ένα σπουργίτι ή μια στρουθοκάμηλος. Π.χ. μπορεί να παρουσιάζεται στο υποκείμενο σε μια λευκή οθόνη μια λέξη που να είναι είτε πτηνό (π.χ.: “χήνα”) είτε όχι (π.χ.: “μπάλα”), και το υποκείμενο να πρέπει να πατήσει όσο πιο γρήγορα μπορεί ένα πλήκτρο με το αριστερό χέρι όταν πρόκειται για πτηνό, και ένα άλλο πλήκτρο με το δεξί χέρι όταν πρόκειται για μη-πτηνό. Κάνοντας το πείραμα, βλέπουμε οτι ο χρόνος απόκρισης π.χ. στο ερέθισμα “στρουθοκάμηλος” είναι πολύ πιο μεγάλος από εκείνον του ερεθίσματος “σπουργίτι”. (Εννοείται οτι γίνονται διορθώσεις για το μήκος της λέξης, δηλ. για το χρόνο που απαιτείται για την ανάγνωσή της.)
 |
 |
|
| Τυπικό μέλος (είδος) της κατηγορίας (έννοιας) “πτηνό” | Ένα καθόλου τυπικό μέλος της ίδιας κατηγορίας |
Αν αντιλαμβανόμασταν τις έννοιες μέσω ορισμών, δεν θα έπρεπε να υπάρχει καμία διαφοροποίηση στο χρόνο απόκρισης, γιατί όσο ικανοποιεί τον υποτιθέμενο ορισμό πτηνού ένα σπουργίτι, άλλο τόσο θα έπρεπε να τον ικανοποιεί και η στρουθοκάμηλος.
Η “θεωρία προτύπου” γα τις έννοιες
Σύμφωνα με την αρχική θεωρία προτύπου, που προτάθηκε το 1973 από την Έλενορ Ρος (Eleanor Rosch) και την ερευνητική-της ομάδα, μια έννοια αντιπροσωπεύεται από το πρότυπό-της, δηλαδή το πρώτο είδος που μας έρχεται στο νου όταν σκεφτόμαστε την κατηγορία εκείνη. Π.χ. στην κατηγορία “πτηνό”, αν το πρώτο παράδειγμα (είδος) που μας έρχεται στο νου είναι το σπουργίτι, αυτό είναι το πρότυπο της κατηγορίας, και μέσω αυτού αντιπροσωπεύεται η κατηγορία. Βέβαια για έναν Αμερικανό το πρότυπο πτηνό μπορεί να είναι άλλο, όπως π.χ. ο κοκκινολαίμης (βλ. προηγούμενη ενότητα).
Αργότερα η Ρος τροποποίησε τον ορισμό της θεωρίας προτύπου, λέγοντας οτι πρότυπο είναι το πιο κεντρικό παράδειγμα, που μπορεί να μην είναι το πρώτο που μας έρχεται στο νου. Π.χ., μπορεί στην κατηγορία “πτηνό” να μας έρχεται στο νου πρώτα το σπουργίτι, αλλά το πρότυπο πτηνό να είναι κάτι που ίσως να μην υπάρχει καν σαν συγκεκριμένο είδος: να είναι μικρό, σε μέγεθος σπουργιτιού, αλλά όχι με τα ειδικά χαρακτηριστικά που μας κάνουν να αναγνωρίζουμε ένα μικρό πετούμενο σαν σπουργίτι. Σίγουρα μπορούμε να ζωγραφίσουμε ένα τέτοιο “μέσο πτηνό”, χωρίς να θεωρούμε οτι ζωγραφίζουμε συγκεκριμένα ένα σπουργίτι:
![]()
Αυτό το “μέσο πτηνό” — που μπορεί και να μην είναι υπαρκτό είδος — είναι το πρότυπο, το οποίο έχει κάποια χαρακτηριστικά, π.χ. πετάει, έχει κοντό λαιμό, κοντό ράμφος, τιτιβίζει, πηδάει στο έδαφος (δεν περπατάει), κλπ. Το αν ένα άλλο είδος ανήκει στην κατηγορία ή όχι εξαρτάται από το πόσο τα χαρακτηριστικά του άλλου είδους είναι παρόμοια με αυτά του προτύπου.
Το μοντέλο πυρήνα–άλω
Η ιδέα οτι πολύπλοκες έννοιες όπως “πτηνό” αντιπροσωπεύονται απλώς και μόνο από έναν κεντρικό εκπρόσωπό τους μοιάζει μάλλον υπεραπλουστευτκή. Από την άλλη μεριά, η κλασική θεωρία καταρρίπτεται από την παρατήρηση και το πείραμα. Το συμπέρασμα από την προηγούμενη κριτική της κλασικής θεωρίας είναι οτι αντί για έναν ορισμό που κάνει αυστηρή διάκριση (σε στυλ άσπρο–μαύρο) μεταξύ “είναι” και “δεν-είναι” στην κατηγορία, φαίνεται να υπάρχει ένα σύνολο μελών που είναι πιο τυπικά, και άλλα μέλη που είναι λιγότερο τυπικά. Π.χ., στην κατηγορία “έπιπλο”, τα είδη “καρέκλα” και “τραπέζι” είναι πολύ κοντά στο κέντρο· ενώ τα είδη “νιπτήρας” και “κάθισμα αυτοκινήτου” είναι πολύ απομακρυσμένα απ’ το κέντρο της έννοιας αυτής. Η θεωρία προτύπου επεκτάθηκε με περισσότερες λεπτομέρειες από τότε που πρωτοδιατυπώθηκε από τη Ρος, ώστε να συμπεριληφθούν οι πειραματικές παρατηρήσεις περί τυπικότητας. Εδώ θα εξετάσουμε τα όσα προσθέτει το μοντέλο που θα ονομάσουμε “μοντέλο πυρήνα–άλω”, το οποίο πρότεινε τη δεκαετία του 1980 ο Αμερικανός νοολόγος Ντάγκλας Χοφστάντερ (Douglas Hofstadter), και υλοποίησε με υπολογιστικά προγράμματα η ερευνητική-του ομάδα. Αργότερα, και άλλοι ερευνητές διατύπωσαν παρόμοια μοντέλα, όπως π.χ. ο Σουηδός νοολόγος Πέτερ Γκάρντενφορς (Peter Gärdenfors). Το μοντέλο πυρήνα–άλω ξεκινάει από την ίδια γενική ιδέα όπως η θεωρία προτύπου, και αποτυπώνεται σχηματικά στο ακόλουθο διάγραμμα:

Στο παραπάνω διάγραμμα
τα τυπικά είδη
πρέπει να τα φανταστούμε σαν σημεία κοντά στο σκοτεινό κέντρο, ενώ τα άτυπα είδη είναι
στην αχνή γκρίζα περιοχή, μακριά από το κέντρο. Σύμφωνα με το μοντέλο
πυρήνα–άλω, ολόκληρη η παραπάνω περιοχή (και όχι μόνο το
πρότυπο είδος) παριστάνει την έννοια. Υπάρχει μια ασαφής κεντρική περιοχή
(σκοτεινό χρώμα) που λέγεται “πυρήνας” (ο
αγγλικός όρος που χρησιμοποιείται στην προκείμενη περίπτωση είναι το “core”),
και μια περιφερειακή, επίσης ασαφής περιοχή (ανοιχτότερο γκρίζο χρώμα) που λέγεται
“άλως” (θηλυκού γένους![]() · αγγλ.: “halo”).
Επειδή η
λέξη “άλως” είναι πολύ σπάνια στη νεοελληνική γλώσσα, θα δώσουμε εδώ
την πλήρη κλίση-της (όπως προκύπτει από την αρχαία) γιατί δεν είναι καθόλου προφανής:
· αγγλ.: “halo”).
Επειδή η
λέξη “άλως” είναι πολύ σπάνια στη νεοελληνική γλώσσα, θα δώσουμε εδώ
την πλήρη κλίση-της (όπως προκύπτει από την αρχαία) γιατί δεν είναι καθόλου προφανής:
|
Νέα Ελληνικά |
Αρχαία Ελληνικά(*) |
||||||||||||
| Ενικός | Πληθυντικός | Ενικός | Πληθυντικός | ||||||||||
| Ονομαστική |
|
|
|
|
|||||||||
| Γενική |
|
|
|
|
|||||||||
| Δοτική |
|
|
|
|
|||||||||
| Αιτιατική |
|
|
|
|
|||||||||
| Κλητική |
|
|
|
|
|||||||||
Όπως σημειώσαμε, δεν υπάρχουν αυστηρά όρια διαχωρισμού μεταξύ πυρήνα και άλω, ούτε καν για το πού ακριβώς τελειώνει η άλως της έννοιας. Υπάρχουν μόνο πιθανότητες να ανήκει ένα είδος στην έννοια, που βαίνουν μειούμενες όσο απομακρυνόμαστε από το κέντρο.
Το παραπάνω διάγραμμα ίσως θυμίζει στον αναγνώστη ένα προηγούμενο: το “πρότυπο τρίγωνο” που προέκυψε από την τοποθέτηση μεγάλου αρθμού τριγώνων το ένα πάνω στο άλλο:

Πράγματι, τα δύο διαγράμματα σχετίζονται, και είναι χρήσιμο να εξετάσουμε τη σχέση-τους, γιατί αυτό θα μας βοηθήσει να κατανοήσουμε τον τρόπο με τον οποίο χτίζονται οι έννοιες κατά το μοντέλο πυρήνα–άλω.
Ας θυμηθούμε οτι το “πρότυπο τρίγωνο” σχηματίστηκε από τα συγκεκριμένα (και “ατελή” όπως θα έλεγε ο Πλάτωνας) παραδείγματα τριγώνων (τα μέλη της έννοιας), τα οποία βάλαμε το ένα πάνω στο άλλο. Με παρόμοιο τρόπο σχηματίζεται και οποιαδήποτε έννοια. Όταν όμως το παράδειγμα το οποίο έχουμε δεν είναι κάτι το απλό και γεωμετρικό όπως ένα τρίγωνο, αλλά πιο σύνθετο, όπως διάφορα είδη πτηνών, τότε αυτό που κάνουμε δεν είναι οτι βάζουμε “πτηνά το ένα πάνω στο άλλο” — πράγμα που θα ήταν γελοίο — αλλά κάνουμε κάτι το ανάλογο με τα χαρακτηριστικά-τους. Το τί σημαίνει αυτό θα εξηγηθεί αμέσως.
Ένα πτηνό έχει πάμπολλα χαρακτηριστικά· όπως π.χ. αναφέρθηκε, μπορεί να πετάει (και με κάποιο βαθμό επιδεξιότητας) ή όχι, έχει ένα λόγο μήκους ράμφους προς μήκος σώματος, έχει βάρος, δύναμη φωνής (κρωξίματος, τιτιβίσματος), ποικιλία χρωμάτων, και πολλά άλλα. Ας πάρουμε να εξετάσουμε, χάριν απλότητας, δύο μόνο χαρακτηριστικά: την ικανότητα πτήσης και την ποικιλία χρωμάτων. Εφόσον έχουμε δύο χαρακτηριστικά προς εξέταση, ας φτιάξουμε στο χαρτί ένα σύστημα συντεταγμένων με δύο άξονες, όπως στο παρακάτω διάγραμμα, όπου ο οριζόντιος άξονας θ’ απεικονίζει την ποικιλία χρωμάτων, και ο κατακόρυφος άξονας την πτητική ικανότητα:
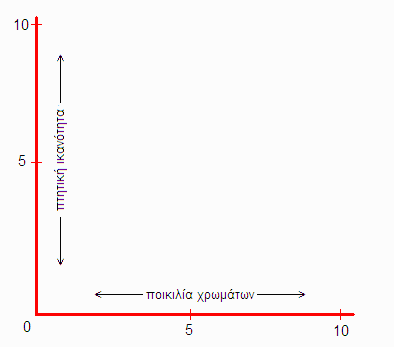
Δηλαδή, για το κάθε είδος πτηνού θα βάζουμε μια κουκκίδα κάπου στο παραπάνω διάγραμμα. Όταν το είδος έχει μεγάλη πτητική ικανότητα (π.χ.: αετοί, γεράκια, χελιδόνια, γλάροι, άλμπατρος, κλπ), τότε η κουκκίδα θα μπαίνει ψηλά στον παραπάνω “χώρο δύο διαστάσεων” (όπου βάλαμε αυθαίρετα την τιμή 10 σαν μέγιστη — δεν έχει σημασία ποια μέγιστη τιμή υιοθετούμε στη βαθμολογία-μας). Είδη με μικρή ή καθόλου πτητική ικανότητα (π.χ.: στρουθοκάμηλοι, πιγκουΐνοι, κότες, κίουϊ, κλπ.) θα τοποθετούνται χαμηλά στο χώρο αυτό. Είδη με λίγα χρώματα (π.χ.: πιγκουΐνοι, χελιδόνια, κλπ.) θα μπαίνουν προς τα αριστερά, ενώ είδη με πολλά χρώματα (π.χ.: παπαγάλοι, παραδείσια πτηνά, κλπ.) θα μπαίνουν προς τα δεξιά. Φυσικά, στο μέσον θα βρίσκονται είδη με μέση ικανότητα πτήσης και μέση ποικιλία χρωμάτων. Ιδού πώς περίπου διαμορφώνεται ο διδιάστατος χώρος-μας με μερικά παραδείγματα:
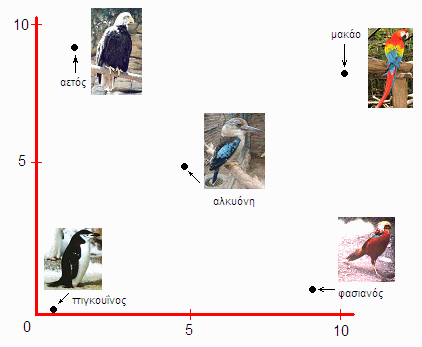
Βλέπουμε τα εξής παραδείγματα: πιγκουΐνοι όπως π.χ. ο Pygoscelis antarctica, κάτω-αριστερά, καθώς δεν πετούν καθόλου και είναι ασπρόμαυροι· αετοί, όπως ο αμερικανικός λευκοκέφαλος (ή “φαλακρός αετός”, Haliaeetus leucocephalus) πάνω-αριστερά, καθώς πετούν πολύ καλά αλλά είναι σχεδόν ασπρόμαυροι· είδη όπως ο “χρυσός φασιανός” (Chrysolophus pictus) κάτω-δεξιά, γιατί έχουν πολλά και έντονα χρώματα, αλλά σπάνια πετούν· το “άρα μακάο” (Ara macao, είδος μεγάλου παπαγάλου της Κεντρικής Αμερικής) πάνω-δεξιά, καθώς πετάει αρκετά καλά, και είναι ένα από τα πιο έντονα χρωματισμένα είδη πτηνών· και κάπου προς το κέντρο τοποθετούνται είδη όπως η κυανόπτερη αλκυόνη (Dacelo leachii, το κουκαμπάρα της Νέας Γουϊνέας και Αυστραλίας), που πετούν με όχι πάνω από μέτρια ικανότητα, και που έχουν κάποια χρώματα αλλά όχι πολλά.
Ας φανταστούμε τώρα όλα τα γνωστά είδη πτηνών τοποθετημένα στο χώρο αυτόν, δηλαδή με μια κουκκίδα για κάθε είδος πτηνού που έχει δει στη ζωή-του ένας άνθρωπος. Πώς θα κατανέμονταν οι κουκκίδες στο διδιάστατο αυτό χώρο; Ιδού πώς, περίπου:
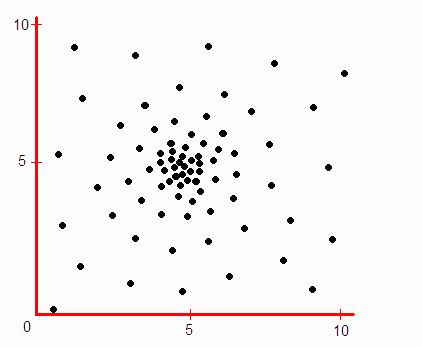
Παρατηρούμε οτι η πλειοψηφία των ειδών βρίσκεται κάπου στο μέσον, γιατί οι ακραίες περιπτώσεις (οποιουδήποτε χαρακτηριστικού, όχι μόνο των δύο που εξετάζουμε) είναι σπάνιες — αυτό είναι γενικός κανόνας στη φύση. Έτσι αν χρησιμοποιήσουμε έντονη (μαύρη) μελάνη στα σημεία με μεγάλη πυκνότητα κουκκίδων, και πιο ανοιχτή (γκρι) όπου είναι μικρότερη, παίρνουμε την εικόνα του χώρου που σημειώσαμε νωρίτερα:
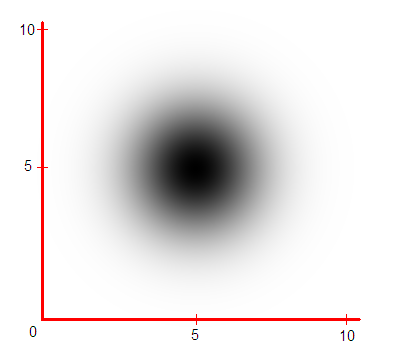
Το παραπάνω διάγραμμα βέβαια είναι δύο διαστάσεων επειδή εξετάσαμε δύο μόνο χαρακτηριστικά των πτηνών, για απλότητα. Αν είχαμε εξετάσει τρία χαρακτηριστικά, θα παίρναμε μια σφαιρική κατανομή κουκκίδων σ’ ένα χώρο τριών διαστάσεων. Όμως τα πτηνά δεν έχουν δύο και τρία χαρακτηριστικά, αλλά δεκάδες. Επομένως για να πλησιάσουμε πιο πολύ την πραγματικότητα πρέπει να χρησιμοποιήσουμε την αφαιρετική ικανότητα του νου για να φανταστούμε ένα χώρο ν διαστάσεων, που δεν μπορεί να παρασταθεί γεωμετρικά. Η ανικανότητά μας όμως να δούμε αυτόν το χώρο ν διαστάσεων (έστω και με τη φαντασία) δεν πρέπει να μας αποτρέψει από το να τον καταλάβουμε: αν τα πτηνά έχουν ν χαρακτηριστικά, τότε και ο χώρος αυτός έχει ν διαστάσεις· η κάθε κουκκίδα (σημείο του χώρου) αντιστοιχεί σε ένα είδος πτηνού, και βρίσκεται εκεί που βρίσκεται γιατί τα ν χαρακτηριστικά-του έχουν συγκεκριμένες τιμές που το τοποθετούν σ’ εκείνη τη θέση — όπως ακριβώς και στις δύο διαστάσεις.
Το μοντέλο πυρήνα–άλω περιλαμβάνει πολύ περισσότερες λεπτομέρειες τις οποίες θα εξετάσουμε αργότερα στο μάθημα αυτό.
Κριτική των θεωριών προτύπου και πυρήνα–άλω
Έχουν διατυπωθεί και κριτικές απόψεις ενάντια στις παραπάνω θεωρίες, κυρίως από φιλοσοφική άποψη (δηλαδή χωρίς να γίνονται πειράματα των οποίων τα αποτελέσματα να αντικρούουν τη θεωρία), και κυρίως από τον Αμερικανό φιλόσοφο και νοολόγο Τζέρυ Φόντορ (Jerry Fodor). Η κριτική βασίζεται στο “πρόβλημα της συνθετικότητας” (αγγλ.: “compositionality”), που είναι το εξής:
![]() Ο
ανθρώπινος νους μπορεί να συνθέτει έννοιες από άλλες
απλούστερες. Ας θεωρήσουμε την έννοια “κατοικίδιο πτηνό”. Προφανώς είναι
σύνθετη, αποτελούμενη από τις έννοιες “κατοικίδιο”, και “πτηνό”. Αν οι
παραπάνω θεωρίες ήσαν σωστές, η σύνθετη έννοια “κατοικίδιο πτηνό” θα
έπρεπε να προκύπτει από ένα συνδυασμό των εννοιών “κατοικίδιο”, και
“πτηνό”. Όμως, η έννοια “κατοικίδιο” έχει σαν τυπικά μέλη το σκύλο και
τη γάτα (αυτές οι έννοιες θα βρίσκονται στον πυρήνα του “κατοικίδιο”),
ενώ η έννοια “πτηνό” έχει στον πυρήνα-της ίσως τα σπουργίτια· σίγουρα όμως
όχι τα καναρίνια ή τα παπαγαλάκια, που είναι πιο τυπικά κατοικίδια
πτηνά. Πώς γίνεται από το συνδυασμό, δηλαδή την ένωση δύο εννοιών που
αντιπροσωπεύονται στους πυρήνες-τους από τους σκύλους και τα σπουργίτια,
να προκύψει κάτι το τόσο διαφορετικό όπως το καναρίνι; Άρα δεν μπορούμε
να κάνουμε σύνθεση εννοιών για να δημιουργήσουμε νέες μέσω των θεωριών
αυτών, οι οποίες έτσι αποτυγχάνουν.
Ο
ανθρώπινος νους μπορεί να συνθέτει έννοιες από άλλες
απλούστερες. Ας θεωρήσουμε την έννοια “κατοικίδιο πτηνό”. Προφανώς είναι
σύνθετη, αποτελούμενη από τις έννοιες “κατοικίδιο”, και “πτηνό”. Αν οι
παραπάνω θεωρίες ήσαν σωστές, η σύνθετη έννοια “κατοικίδιο πτηνό” θα
έπρεπε να προκύπτει από ένα συνδυασμό των εννοιών “κατοικίδιο”, και
“πτηνό”. Όμως, η έννοια “κατοικίδιο” έχει σαν τυπικά μέλη το σκύλο και
τη γάτα (αυτές οι έννοιες θα βρίσκονται στον πυρήνα του “κατοικίδιο”),
ενώ η έννοια “πτηνό” έχει στον πυρήνα-της ίσως τα σπουργίτια· σίγουρα όμως
όχι τα καναρίνια ή τα παπαγαλάκια, που είναι πιο τυπικά κατοικίδια
πτηνά. Πώς γίνεται από το συνδυασμό, δηλαδή την ένωση δύο εννοιών που
αντιπροσωπεύονται στους πυρήνες-τους από τους σκύλους και τα σπουργίτια,
να προκύψει κάτι το τόσο διαφορετικό όπως το καναρίνι; Άρα δεν μπορούμε
να κάνουμε σύνθεση εννοιών για να δημιουργήσουμε νέες μέσω των θεωριών
αυτών, οι οποίες έτσι αποτυγχάνουν.
Μια απάντηση στην κριτική αυτή είναι οτι “σύνθεση εννοιών” στην περίπτωση του “κατοικίδιο πτηνό” δεν σημαίνει το να δούμε τις έννοιες “κατοικίδιο” και “πτηνό” σαν δύο ουσιαστικά και να κάνουμε κάτι με τους πυρήνες-τους. Εδώ το “κατοικίδιο” είναι επίθετο, όχι ουσιαστικό όπως το “πτηνό”, επομένως σαν επίθετο προσδιορίζει το ουσιαστικό, δηλαδή περιορίζει τις ιδιότητές του· μας λέει οτι δεν πρόκειται για ένα οποιοδήποτε πτηνό, αλλά για κάποιο που είναι κατοικίδιο. Εφόσον λοιπόν έχουμε ένα επίθετο (το “κατοικίδιο”) σύνθεση εννοιών γίνεται παίρνοντας τις ιδιότητες που ανήκουν στον πυρήνα του “κατοικίδιο”, όπως: “ζει κοντά-μας”, “τρέφεται από εμάς”, “μας ευχαριστεί η παρουσία-του”, κλπ., και μ’ αυτές περιορίζουμε το ουσιαστικό (ή το “προσδιορίζουμε”, εξ ου και “επιθετικός προσδιορισμός”). Το λάθος που κάνουν όσοι διατυπώνουν αυτή την κριτική είναι οτι νομίζουν πως το “κατοικίδιο” εδώ είναι ουσιαστικό (πιθανώς παρασυρόμενοι από την αγγλική γλώσσα, όπου πρακτικά οποιοδήποτε ουσιαστικό μπορεί να ιδωθεί και σαν επίθετο, οπότε χρειάζεται νοητική προσπάθεια για να καταλάβει κανείς πότε μια λέξη παίζει ρόλο ουσιαστικού και πότε επιθέτου), με αποτέλεσμα να εξετάζουν τον πυρήνα του ουσιαστικού “κατοικίδιο” (που περιλαμβάνει έννοιες όπως “γάτα”, “σκύλος”, κλπ.), και όχι του επιθέτου (που περιλαμβανει ιδιότητες, όπως αυτές που προαναφέρθηκαν).
![]() Άλλη
κριτική βασίζεται στο πρόβλημα των αρνήσεων. Ας θεωρήσουμε την πρόταση:
“Ο Ρούντυ δεν είναι σκύλος”. Το “δεν είναι σκύλος”, λέει η άποψη αυτή,
ως έννοια, πρέπει να έχει ένα πρότυπο, με πυρήνα και κάποια άλω.
Όμως τί μπορεί να ανήκει στον πυρήνα της έννοιας “μη σκύλος”; Τίποτα
απολύτως, αφού οι έννοιες που δεν ανήκουν στην κατηγορία “σκύλος” είναι
οτιδήποτε, και δεν δημιουργούν συγκεκριμένο πυρήνα, γιαυτό δεν υπάρχει
πρότυπο “μη σκύλου”. Άρα η θεωρία προτύπου με το μοντέλο
πυρήνα–άλω δεν εξηγεί το πώς παριστάνουμε τις έννοιες που δημιουργούνται μέσω
αρνήσεων.
Άλλη
κριτική βασίζεται στο πρόβλημα των αρνήσεων. Ας θεωρήσουμε την πρόταση:
“Ο Ρούντυ δεν είναι σκύλος”. Το “δεν είναι σκύλος”, λέει η άποψη αυτή,
ως έννοια, πρέπει να έχει ένα πρότυπο, με πυρήνα και κάποια άλω.
Όμως τί μπορεί να ανήκει στον πυρήνα της έννοιας “μη σκύλος”; Τίποτα
απολύτως, αφού οι έννοιες που δεν ανήκουν στην κατηγορία “σκύλος” είναι
οτιδήποτε, και δεν δημιουργούν συγκεκριμένο πυρήνα, γιαυτό δεν υπάρχει
πρότυπο “μη σκύλου”. Άρα η θεωρία προτύπου με το μοντέλο
πυρήνα–άλω δεν εξηγεί το πώς παριστάνουμε τις έννοιες που δημιουργούνται μέσω
αρνήσεων.
Απάντηση στην κριτική αυτή είναι οτι το “όχι σκύλος” δεν είναι έννοια. Δεν είναι έννοιες όλα όσα μπορούμε να κατασκευάσουμε μέσω εννοιών. Το “σκύλος” είναι φυσικά μια έννοια· το “άρνηση” (σαν ουσιαστικό) είναι επίσης έννοια· όμως το “όχι” (ή το “δεν”, ή το “μη”) που βάζουμε πριν από το “σκύλος” δεν είναι έννοια, αλλά ένας τελεστής που εφαρμόζει επί εννοιών, και που το αποτέλεσμά του δεν είναι έννοια αλλά συντακτική δομή.(*) Όταν λέμε οτι ο νους είναι ένα “πολύπλοκο σύστημα” που αποτελείται από έννοιες, δεν εννοούμε οτι αποτελείται μόνο από έννοιες. Όπως ένας εγκέφαλος δεν αποτελείται μόνο από νευρώνες (υπάρχουν και τα κύτταρα που “ντύνουν” τους άξονες των νευρώνων με μυελίνη, υπάρχουν τα αιμοφόρα αγγεία, κ.ά. — βλ. μαθ. Ε3 ή Ε4)· όπως ένας γαλαξίας δεν αποτελείται μόνο από αστέρια (υπάρχουν πλανήτες, κομήτες, διαστρική ύλη, μαύρες τρύπες, κ.ά.)· όπως ένας οργανισμός δεν αποτελείται μόνο από κύτταρα (υπάρχουν τα διάφορα υγρά, και άλλες ουσίες μη κυτταρικής υφής)· έτσι και ένας νους δεν αποτελείται μόνο από έννοιες. Οι έννοιες παίζουν μεν πρωτεύοντα ρόλο, αλλά δεν είναι τα αποκλειστικά δομικά υλικά από τα οποία χτίζεται ένας νους.
Η θεωρία παραδειγμάτων
Κανονικά όσα αναφέρθηκαν μέχρι τώρα θα ήσαν αρκετά σαν ένα ξεκίνημα για τη θεώρηση από υψηλό επίπεδο της δόμησης του νου μέσω εννοιών. Όμως πολλοί νοολόγοι ενδιαφέρονται όχι απλώς για τη σε υψηλό επίπεδο θεώρηση του νου, αλλά και για το τί κάνει ο εγκέφαλος σε χαμηλό επίπεδο. Πώς αποθηκεύει τις έννοιες ο εγκέφαλος; Η γνώση αυτή είναι απαραίτητη για όποιον θέλει να κάνει τη σύνδεση μεταξύ νου και εγκεφάλου, και να μάθει πώς οι νευρώνες “αναφύουν” (ή “προκαλούν”) την εμφάνιση του νου.
Παρόλο που η απάντηση σ’ αυτό το ερώτημα δεν είναι γνωστή ακόμα, εντούτοις πειράματα που έγιναν (και γίνονται) δείχνουν οτι είναι πιθανό ο εγκέφαλος να μην αποθηκεύει ούτε πρότυπα ούτε δομές πυρήνων–άλων στους νευρώνες-του, αλλά συγκεκριμένα παραδείγματα ειδών, “κυριολεκτικά”, όπως τα έχει προσλάβει μέσω των αισθήσεων. Δηλαδή, ενώ από την προηγούμενη ενότητα συνάγεται οτι αυτό που αποθηκεύει ο νους είναι αντικείμενα στατιστικής φύσης (π.χ. μέσες τιμές χαρακτηριστικών), ο εγκέφαλος μπορεί να μην αποθηκεύει στατιστικές, αλλά τα δεδομένα στην ολότητά τους, “κατά κυριολεξία”. Στη συνέχεια, όταν θέλουμε να σκεφτούμε π.χ. ένα πτηνό, τότε ο εγκέφαλος υπολογίζει αυτόματα αυτό που μας φαίνεται σαν “τυπικό πτηνό” (π.χ. για τους Έλληνες κάτι που “σπουργιτοφέρνει”) κατευθείαν από όλα τα παραδείγματα που έχει αποθηκευμένα, και το προωθεί στο συνειδητό, οπότε δίνουμε την απάντηση. Ο υπολογισμός του στατιστικού μέσου από δεκάδες, ή εκατοντάδες παραδείγματα γίνεται χωρίς χρονική καθυστέρηση γιατί οι νευρώνες λειτουργούν παράλληλα, και άρα δεν καθυστερούν περιμένοντας ο ένας τον άλλον. Τουλάχιστον αυτό θα μπορούσε να είναι η εξήγηση του πώς ένα πολύπλοκα υπολογιζόμενο αποτέλεσμα, όπως αυτό του στατιστικού μέσου, γίνεται με τόση αμεσότητα — αν η “θεωρία παραδειγμάτων” περί αποθήκευσης στον εγκέφαλο είναι σωστή.
Όπως αναφέρθηκε, η πειραματική έρευνα δείχνει να υποστηρίζει τη θεωρία παραδειγμάτων. Έτσι έχει δημιουργηθεί μια αντιπαλότητα μεταξύ των υποστηρικτών των θεωριών προτύπου κ’ εκείνων της θεωρίας παραδειγμάτων, αφού κ’ οι δυο θεωρίες έχουν πειραματική υποστήριξη. Αυτό που — κατά τη γνώμη του συγγραφέα του παρόντος — δημιουργεί τη σύγχυση είναι οτι πολλοί νοολόγοι, όταν επιχειρηματολογούν για το ποια από τις δυο θεωρίες είναι σωστή, δεν κάνουν διάκριση μεταξύ νου και εγκεφάλου· δηλαδή θεωρούν οτι καί οι δυο θεωρίες περιγράφουν το πώς λειτουργεί ο εγκέφαλος· επομένως, αναμένουν οτι η μια θεωρία πρέπει να είναι σωστή και η άλλη λάθος, αφού πρέπει να υπάρχει ένας συγκεκριμένος τρόπος με τον οποίο αποθηκεύονται οι έννοιες στον εγκέφαλο. Το ψευδοδίλημμα όμως εξαφανίζεται αν κάνουμε διάκριση μεταξύ νου και εγκεφάλου. Μπορεί σε χαμηλό επίπεδο ο εγκέφαλος να αποθηκεύει τα συγκεκριμένα παραδείγματα που γίνονται αντιληπτά με τις αισθήσεις-μας. “Εμείς” όμως δεν έχουμε πρόσβαση στις λειτουργίες του εγκεφάλου σε χαμηλό επίπεδο — δεν μας απασχολεί το τί κάνουν οι νευρώνες-του. “Εμείς”, δηλαδή ο νους-μας σε υψηλό επίπεδο, αντιλαμβάνεται στατιστικές χαρακτηριστικών (θεωρίες προτύπου & πυρήνα–άλω). Οι στατιστικές είναι απόλυτα δεκτές σαν “στοιχεία” με τα οποία χτίζονται οι έννοιες, όντας στοιχεία ενός ανώτερου επιπέδου: του νου. Δεν έχει νόημα να πούμε οτι «στην πραγματικότητα οι στατιστικές δεν είναι τα “σωστά” υλικά με τα οποία χτίζονται οι έννοιες, επειδή οι στατιστικές αυτές υπολογίζονται από συγκεκριμένα παραδείγματα», όπως δεν έχει νόημα στη φυσική να υποστηρίξουμε οτι η θερμοκρασία «δεν υπάρχει στην πραγματικότητα», επειδή είναι μια στατιστική ιδιότητα που προκύπτει από τη μέση συμπεριφορά τεράστιου αριθμού μορίων· άλλο το μακροσκοπικό επίπεδο, όπου προκύπτουν αναφυόμενες ιδιότητες όπως η θερμοκρασία, και άλλο το μικροσκοπικό επίπεδο, όπου υπάρχουν μόνο μόρια που κινούνται άτακτα. Παρόμοια, άλλο το επίπεδο του νου (των εννοιών με τις στατιστικής φύσης αναφυόμενες ιδιότητές τους) και άλλο του εγκεφάλου (των νευρώνων με τα ιδιαίτερα χαρακτηριστικά-τους).
Ενδιαφέρον είναι το οτι αυτό που περιγράφεται στην επόμενη ενότητα σαν “Πρώτος Νόμος της νοολογίας” προέκυψε από πειράματα που έκαναν οι ερευνητές που υποστήριζαν τη θεωρία παραδειγμάτων, προκειμένου να υποστηρίξουν τη θεωρία αυτή. Όπως θα δούμε όμως, το θέμα ξεπερνάει τα στενά όρια της συγκεκριμένης θεωρίας και εφαρμόζεται γενικότερα.
Νοολογικοί νόμοι
Θα δούμε στη συνέχεια ορισμένους νόμους της νοολογίας, που ονομάζονται έτσι γιατί είναι υποχρεωτικοί. Αυτό σημαίνει οτι ο οποιοσδήποτε νους υπακούει στους νόμους αυτούς, είτε το θέλει, είτε όχι· είτε είναι ευφυής, είτε κουτός· είτε σκέφτεται ενσυνείδητα, είτε υποσυνείδητα. Για να το πούμε αλλιώς, ο νους του ανθρώπου είναι ανίκανος να παραβιάσει τους νόμους αυτούς, επομένως υπακούει σ’ αυτούς. Περιληπτικά, οι νόμοι που περιγράφονται στο παρόν μάθημα είναι οι εξής:
-
Κατηγοριοποίηση: πώς δημιουργούμε τις κατηγορίες εννοιών.
-
Απομόνωση πυρήνα: πώς ανιχνεύουμε και συγκρατούμε τον πυρήνα μιας έννοιας· τί συνέπειες έχει αυτή η ικανότητα.
-
Συμπλήρωση μοτίβου: πώς προβλέπουμε αυτό που λείπει, ή ακόμα και το μέλλον.
-
Ελαχιστοποίηση δομής: πώς μέσω του “ξυραφιού του Όκαμ (Ockham)” κατανοούμε τη δομή των εννοιών.
-
Ποσοτική αντίληψη: πώς αντιλαμβανόμαστε το μέγεθος και την ποσότητα.
-
Δημιουργία συσχετισμών: πώς (και πότε) δημιουργούμε συσχετισμούς μεταξύ εννοιών.
Ας εξετάσουμε τώρα αναλυτικά τους νόμους αυτούς.
Πρώτος Νόμος: Κατηγοριοποίηση
Στο παράδειγμα της προηγούμενης ενότητας θεωρήσαμε τα πτηνά σαν μία έννοια, οπότε είδαμε οτι εξετάζοντας δύο χαρακτηριστικά (την πτητική ικανότητα και την ποικιλία χρωμάτων) παίρνουμε μια κατανομή κουκκίδων σε ένα χώρο δύο διαστάσεων. Οι κουκκίδες (μία για κάθε είδος πτηνού) κατανέμονται έτσι ώστε να βρίσκονται πιο πολλές σε μια κεντρική περιοχή (πυρήνα), και προοδευτικά λιγότερες όσο απομακρυνόμαστε από το κέντρο (προς την άλω).
Τί θα συνέβαινε αν
αντί για μία έννοια (“πτηνό”) θεωρούσαμε δύο έννοιες![]() ; Π.χ., οι δύο
έννοιες θα μπορούσαν να είναι “λαχανικό” και “φρούτο”· και τα δύο
χαρακτηριστικά-τους (δύο, επειδή τόσα μόνο μπορούμε να απεικονίσουμε σε
επίπεδη σελίδα) να είναι π.χ. η γλυκύτητα (ποσοστό σακχάρων) του φρούτου
ή λαχανικού στον οριζόντιο άξονα, και η σκληρότητα της φλούδας στον
κατακόρυφο άξονα. Αν τοποθετήσουμε μια κουκκίδα για κάθε είδος φρούτου ή
λαχανικού σε χώρο δύο διαστάσεων, όπως προηγουμένως, θα πάρουμε πιθανώς
μια κατανομή όπως η ακόλουθη:
; Π.χ., οι δύο
έννοιες θα μπορούσαν να είναι “λαχανικό” και “φρούτο”· και τα δύο
χαρακτηριστικά-τους (δύο, επειδή τόσα μόνο μπορούμε να απεικονίσουμε σε
επίπεδη σελίδα) να είναι π.χ. η γλυκύτητα (ποσοστό σακχάρων) του φρούτου
ή λαχανικού στον οριζόντιο άξονα, και η σκληρότητα της φλούδας στον
κατακόρυφο άξονα. Αν τοποθετήσουμε μια κουκκίδα για κάθε είδος φρούτου ή
λαχανικού σε χώρο δύο διαστάσεων, όπως προηγουμένως, θα πάρουμε πιθανώς
μια κατανομή όπως η ακόλουθη:
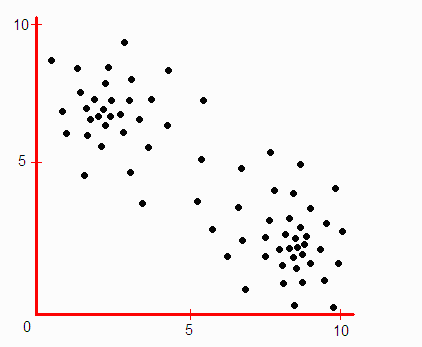
Η κατανομή αυτή είναι σαν να μας λέει “υπάρχουν δύο έννοιες”, γιατί βλέπουμε τις κουκκίδες να είναι περισσότερο συγκεντρωμένες σε δύο περιοχές. Π.χ. η πάνω-αριστερά συγκέντρωση θα μπορούσε να αντιστοιχεί στα λαχανικά (λιγότερο γλυκά και με πιο σκληρή φλούδα) και η κάτω-δεξιά συγκέντρωση στα φρούτα (πιο γλυκά, και με πιο μαλακή φλούδα). Αν φανταστούμε ν διαστάσεις αντί για δύο, και πάλι τα φρούτα θα συγκεντρώνονται σε μια περιοχή (έστω και μη απεικονιζόμενη, καθώς θα είναι ν διαστάσεων), με κάποια πιο τυπικά από άλλα, ενώ τα λαχανικά σε άλλη περιοχή. Θα υπάρχουν και κάποια είδη, όπως οι ντομάτες και οι ελιές, που θα βρίσκονται στο χώρο μεταξύ των δύο περιοχών, μη κατηγοριοποιούμενα ξεκάθαρα σε μια από τις δυο περιοχές. Ιδού τώρα ποια είναι η σημαντικότητα των παραπάνω παρατηρήσεων:
Έστω οτι ερχόμαστε στον κόσμο χωρίς να γνωρίζουμε οτι υπάρχουν αυτές οι δυο κατηγορίες, δηλαδή τα φρούτα και τα λαχανικά. Μπορεί να είμαστε νήπια, και να βλέπουμε διάφορα παραδείγματα φρούτων και λαχανικών, χωρίς κανένας να μας λέει: «Ξέρεις, αυτό που βλέπεις τώρα είναι ένα φρούτο.» Ακόμα κι αν μας έλεγε κανείς κάτι τέτοιο (δηλαδή αν ένας παιδαγωγός — π.χ. γονέας — μας βοηθούσε ν’ αντιληφθούμε τις δύο κατηγορίες), μπορεί να μην ξέραμε καν τη γλώσσα για να καταλάβουμε τις λέξεις. Στη γενική περίπτωση, αν το καλοσκεφτούμε, τα νήπια δεν έχουν όλη την ώρα κάποιον κοντά-τους για να τους βοηθά με το πώς να σχηματίζουν τις κατηγορίες. Πρέπει από μόνα-τους να μπορούν να βρουν οτι, π.χ., υπάρχει αυτή η κατηγορία (έστω κι αν δεν ξέρουν τη λέξη “φρούτο”) και η άλλη κατηγορία (και πάλι χωρίς να γνωρίζουν οτι της αντιστοιχεί μια λεξη, το “λαχανικό”). Όμως δεν πρόκειται μόνο για τα νήπια, αλλά για εμάς τους ίδιους. Στην καθημερινή πράξη σχηματίζουμε κατηγορίες χωρίς κανείς να μας βοηθά, απλώς βλέποντας τα παραδείγματα. Π.χ. μπορεί να βλέπουμε διάφορους τύπους προσώπων από άλλες χώρες, και να σχηματίζουμε στο νου-μας κάποιες κατηγορίες, χωρίς να ξέρουμε οτι ο ένας τύπος προσώπων λέγεται “Αιθίοπες”, ενώ ο άλλος “Σομαλοί”. Πώς τα καταφέρνουμε να σχηματίζουμε τις κατηγορίες (τις έννοιες) δεδομένων των “κουκκίδων”, δηλαδή των παραδειγμάτων που υποπίπτουν στην αντίληψή μας ένα-ένα; Αυτό το ερώτημα απαντά ο Πρώτος Νόμος.
Ας ξαναθεωρήσουμε το προηγούμενο διάγραμμα, και ας φανταστούμε το διδιάστατο χώρο αρχικά λευκό (κενό), και τις κουκκίδες να φτάνουν σ’ αυτό μία-μία. Μπορούμε μήπως να γράψουμε ένα πρόγραμμα στον υπολογιστή, δηλαδή έναν αλγόριθμο, ο οποίος να αντιλαμβάνεται οτι υπάρχουν δύο ομάδες κουκκίδων (αφού φτάσει ικανός αριθμός-τους στο χώρο), όπως αντιλαμβάνεται αυτό το πράγμα και το ανθρώπινο μάτι; Αν είχαμε έναν τέτοιον αλγόριθμο θα μπορούσαμε να πούμε οτι και ένας υπολογιστής μπορεί ν’ αντιληφθεί δύο κατηγορίες (δύο έννοιες): την κατηγορία εκείνων των κουκκίδων, και την κατηγορία των άλλων κουκκίδων — παρόλο που, όπως ένα νήπιο, ο υπολογιστής δεν θα γνωρίζει τις λέξεις “λαχανικό” και “φρούτο” για να τις εκχωρήσει στις δύο κατηγορίες.
Προκειμένου να φτιάξουμε τον αλγόριθμο που αντιλαμβάνεται δύο κατηγορίες (ομάδες κουκκίδων) στο προηγούμενο διάγραμμα, πρέπει πρώτα να ορίσουμε την απόσταση μεταξύ δύο κουκκίδων.
Η απόσταση μεταξύ δύο κουκκίδων δίνεται με απλούστατο τρόπο από τη γεωμετρία του γυμνασίου, ως εξής: η κάθε κουκκίδα έχει δύο συντεταγμένες, x και y, όπου το x είναι η τιμή της γλυκύτητας στο παράδειγμά μας (οριζοντιος άξονας), και το y είναι η τιμή της σκληρότητας της φλούδας (κατακόρυφος άξονας). Έτσι, θα συμβολίζουμε μια κουκκίδα με το (x, y), όπου τα x και y είναι αριθμοί. Αν λοιπόν η μία κουκκίδα έχει συντεταγμένες (x1, y1), και η άλλη κουκκίδα έχει συντεταγμένες (x2, y2), τότε η μεταξύ-τους απόσταση d δίνεται από τον τύπο:
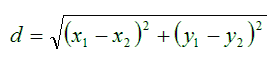
Αυτός ο τύπος δίνει την “Ευκλείδεια απόσταση” μεταξύ δύο σημείων (κουκκίδων) του επιπέδου: των σημείων (x1, y1) και (x2, y2). Υπάρχουν και άλλες αποστάσεις εκτός από την Ευκλείδεια, αλλά η Ευκλείδεια είναι η απλούστερη και πιο “φυσική” γεωμετρική απόσταση.
| Παράδειγμα: Έστω οτι το ένα είδος είναι η μελιτζάνα, με (x1, y1) ίσο με (1, 8) (δηλαδή: γλυκύτητα 1 — σχεδόν καθόλου — και σκληρότητα 8 — αρκετά μεγάλη)· το δεύτερο είδος (x2, y2) έστω οτι είναι το μήλο, ίσο με (7, 3) (αρκετά γλυκό, με μάλλον μαλακή φλούδα). Βάζοντας τις τιμές αυτές στον παραπάνω τύπο έχουμε: (1 – 7)2 + (8 – 3)2 = 36 + 25 = 61, του οποίου η τετραγωνική ρίζα είναι περίπου 7,81. Τόση λοιπόν είναι η Ευκλείδεια απόσταση μεταξύ μήλου και μελιτζάνας, αλλά προσοχή: βάσει των δύο μόνο χαρακτηριστικών (γλυκύτητας και σκληρότητας) στα οποία εστιάσαμε την προσοχή-μας. |
Αν οι διαστάσεις (δηλαδή τα χαρακτηριστικά των ειδών-μας) είναι όχι 2 αλλά ν, τότε η κάθε κουκκίδα θα έχει ν συντεταγμένες, οπότε θα συμβολίζεται σαν (x, y, ... z), (όπου το πλήθος των γραμμάτων θα είναι ν) και ο παραπάνω τύπος για την απόσταση d γενικεύεται απλούστατα:
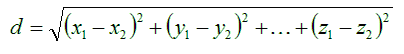
Η ψυχολογία όμως δεν είναι ακριβώς γεωμετρία. Στην ανθρώπινη ψυχολογία μπορεί το ένα χαρακτηριστικό (π.χ. η σκληρότητα) να παίζει κάποιο ρόλο σήμερα, αλλά να παίζει μεγαλύτερο ή μικρότερο ρόλο αύριο — ακόμα και στο νου του ίδιου ανθρώπου — επειδή σύμφωνα με τα ερεθίσματα που δέχτηκε ο άνθρωπος εντωμεταξύ, η σπουδαιότητα του χαρακτηριστικού μεγάλωσε ή μίκρυνε. Αυτή η παρατήρηση έχει ελεγχθεί πειραματικά. Μπορεί π.χ. τη μία ημέρα να έχουμε ορισμένες τιμές χαρακτηριστικών στο νου-μας για τα φρούτα και λαχανικά· την επόμενη όμως ημέρα, ο ψυχολόγος στο εργαστήριο μπορεί πρώτα να μας δώσει να διαβάσουμε ένα κείμενο περί σκληρότητας πολύτιμων λίθων (διαμάντια, ρουμπίνια, κλπ), και μετά να επαναλάβει το πείραμα της προηγούμενης ημέρας. Έτσι, έχοντας έμεσα “πριμοδοτήσει” την έννοια “σκληρότητα”, όταν έρθει η ώρα να ελέγξει την απόσταση που αποδίδουμε μεταξύ διαφόρων φρούτων και λαχανικών, θα βρει οτι η σκληρότητα τώρα παίζει μεγαλύτερο ρόλο στο νου-μας, παρόλο που κανείς δεν μας είπε να δώσουμε μεγαλύτερη προσοχή στο χαρακτηριστικό αυτό όταν συγκρίνουμε φρούτα και λαχανικά.
Αυτού του είδους η “πριμοδότηση” εννοιών (όπως η σκληρότητα στο παράδειγμα) συμβαίνει ανά πάσα στιγμή στο νου του ανθρώπου, και για τους πιο απροσδόκητους λόγους. Πρέπει επομένως ο τύπος που μας δίνει την απόσταση d μεταξύ δύο εννοιών να είναι αντίστοιχα ευέλικτος, ώστε να προβλέπει και την πριμοδότηση των χαρακτηριστικών. Αυτό γίνεται πολύ εύκολα, προσθέτοντας βάρη σε κάθε διάσταση του τύπου. Στον τύπο που ακολουθεί, τα βάρη συμβολίζονται με το w:
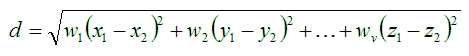
Δηλαδή, αν η σκληρότητα (του προηγούμενου παραδείγματος) είναι η διάσταση i, τότε όταν είναι “πριμοδοτημένη” στο νου-μας (οπότε παίζει μεγαλύτερο ρόλο), το αντίστοιχο βάρος-της wi θα έχει μεγάλη τιμή· αν όχι, το wi θα έχει μικρή τιμή. Έτσι, “παίζοντας” με τις τιμές των βαρών w, μπορούμε να φανταστούμε τις έννοιες να αλλάζουν τις αποστάσεις μεταξύ-τους με δυναμικό τρόπο, ανάλογα με το πώς αισθάνεται ο νους που τις χειρίζεται εκείνη την ώρα και με το ποια ερεθίσματα έχει δεχτεί πιο πρόσφατα.
Η μόνη απαίτηση στον παραπάνω τύπο είναι οτι το άθροισμα των βαρών w1 + w2 + ... wν πρέπει να είναι ίσο με 1. Αυτός είναι και ο 1ος τύπος αυτού που ονομάζουμε “Γενικευμένο Μοντέλο Περιβάλλοντος” ή ΓΜΠ (αγγλ.: Generalized Context Model). Το ΓΜΠ πρότεινε τις δεκαετίες του 1980 και 1990 ο Αμερικανός πειραματικός ψυχολόγος Ρόμπερτ Νοσόφσκυ (Robert Nosofsky).
Εφοδιασμένοι με τον τύπο που δίνει την (εννοιολογική) απόσταση μεταξύ ειδών, μπορούμε τώρα να ορίσουμε το τί είναι η ομοιότητα (s, από το αγγλ.: similarity) μεταξύ ειδών. Η ομοιότητα s δίνεται από το 2ο τύπο του ΓΜΠ:
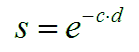
Το e στον παραπάνω τύπο είναι μια μαθηματική πράξη (η λεγόμενη “εκθετική συνάρτηση”), η οποία περιλαμβάνεται σχεδόν πάντα στα “επιστημονικά κομπιουτεράκια”, σαν ένα κουμπί. Δηλαδή πληκτρολογούμε έναν αριθμό, πατάμε το κουμπί που σημειώνεται με το ex, και βλέπουμε το αποτέλεσμα στην οθόνη. Το d είναι η απόσταση που υπολογίστηκε με τον προηγούμενο τύπο, ενώ το c είναι μια παράμετρος, που όταν της δίνουμε μεγάλη τιμή τότε ο αλγόριθμός μας (τον οποίο θα περιγράψουμε, και που θα χρησιμοποιεί την ομοιότητα s) δημιουργεί πολλές κατηγορίες (ίσως και περισσότερες απ’ όσες αντιλαμβάνεται συνήθως ο άνθρωπος)· και αντίστροφα: μικρές τιμές στην παράμετρο c κάνουν τον αλγόριθμο ν’ αντιλαμβάνεται λίγες κατηγορίες.
Εννοείται οτι οι παραπάνω τύποι του ΓΜΠ δεν είναι αυθαίρετοι, αλλά έχουν προκύψει μετά από εργαστηριακές παρατηρήσεις υποκειμένων (ατόμων), και μετά από πάμπολλες επαναλήψεις των πειραμάτων αυτών. Δηλαδή οι άνθρωποι συμπεριφέρονται σαν να ακολουθούν τους παραπάνω τύπους (με κάποια δεδομένη τιμή για το c).
Τώρα, έχοντας την ομοιότητα s μεταξύ ειδών, μένει να δούμε πώς δημιουργούνται οι κατηγορίες των ειδών. Εδώ θα περιγράψουμε δύο διαφορετικές μεθόδους.
Μία μέθοδος δίνεται από τον 3ο τύπο του ΓΜΠ (που προκύπτει πάντα μέσω πειραματικών παρατηρήσεων), και αφορά στον τρόπο με τον οποίο ο ανθρώπινος εγκέφαλος μοιάζει να αποφασίζει πώς να εκχωρεί αντικείμενα σε κατηγορίες. Σύμφωνα λοιπόν με το ΓΜΠ, όταν έρχεται μια νέα κουκκίδα, η υπ’ αριθμόν i, υπάρχει μια πιθανότητα P να την κατατάξουμε στην κατηγορία J (που έστω οτι έχουμε δημιουργήσει ήδη), και η πιθανότητα αυτή P (J | i) δίνεται από τον τύπο:
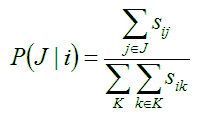
όπου με το σύμβολο Σ συμβολίζεται το άθροισμα ποσοτήτων, το sij είναι η ομοιότητα μεταξύ των ειδών i και j, ενώ το K είναι το σύνολο όλων των κατηγοριών που σχηματίσαμε με τα δοσμένα είδη. Η κατανόηση του 3ου τύπου είναι απλή, αλλά όχι απαραίτητη.(*)
Ας σημειώσουμε όμως οτι ο παραπάνω φορμαλιστικός τρόπος δεν είναι ο μοναδικός. Ο “υπολογιστικά δαπανηρός” αυτός τύπος είναι μάλλον το αναφυόμενο αποτέλεσμα (η “συνισταμένη”) της εργασίας δισεκατομμυρίων νευρώνων του εγκεφάλου. Σαν τύπος δεν είναι καθόλου βολικός για χρήση σε υπολογιστή, γιατί απαιτεί τον υπολογισμό αθροισμάτων (και μάλιστα διπλών, το ένα μέσα στο άλλο), που υπολογίζονται επί όλων των ειδών που έχουμε αντιληφθεί μέχρι στιγμής, όλων των κατηγοριών που έχουμε κατασκευάσει. Τέτοιοι υπολογισμοί, παρόλο που είναι “απλοί” για εγκεφαλικούς νευρώνες που λειτουργούν παράλληλα και κατά δισεκατομμύρια, είναι συνήθως “προς αποφυγή” από προγράμματα υπολογιστών, που λειτουργούν εκτελώντας πράξεις μία-μία.(*)
Επιπλέον, ο τύπος αυτός μας δίνει μόνο την πιθανότητα του να ανήκει ένα είδος σε μία κατηγορία· δεν μας απαντά όμως στο πότε να κατασκευάσουμε μια νέα κατηγορία.(*)
Ας σημειωθεί οτι και στη θεωρία προτύπου ένας παρόμοιος τύπος δίνει την πιθανότητα να ανήκει ένα είδος σε μια κατηγορία.(*)
Μια άλλη απάντηση για το πώς δημιουργούνται οι κατηγορίες μπορεί να δοθεί από διάφορους αλγορίθμους κατηγοριοποίησης, που γίνονται πιο εύκολα κατανοητοί, και υλοποιούνται με στοιχειώδη τρόπο σε υπολογιστή. Ένα πολύ απλό παράδειγμα αλγορίθμου κατηγοριοποίησης είναι το εξής:
Ένας απλός αλγόριθμος κατηγοριοποίησης:
Βήμα 1: Πάρε ένα από τα είδη που πρόκειται να κατηγοριοποιηθούν.
Βήμα 2: Βρες την κοντινότερη κατηγορία όπου μπορεί να μπει το είδος αυτό.
Βήμα 3: Αν δεν υπάρχει καμία τέτοια κατηγορία τότε
Βήμα 4: δημιούργησε μια νέα (κενή) κατηγορία.
Βήμα 5: Πρόσθεσε το είδος στην κατηγορία αυτή.
Βήμα 6: Αν υπάρχουν κι άλλα είδη προς κατηγοριοποίηση, πήγαινε πίσω στο Βήμα 1.
Προφανώς όμως ο παραπάνω αλγόριθμος στο Βήμα 2 είναι ελλιπής, γιατί δεν ορίζει πώς βρίσκουμε την “κοντινότερη κατηγορία”. Αυτό γίνεται με τον παρακάτω “υπο-αλγόρθιμο”:
Αλγόριθμος “κοντινότερης κατηγορίας” για δοσμένο είδος ε:
Βήμα 1: Αρχικά σημείωσε σαν “καμία” την κοντινότερη κατηγορία,
και το 0 σαν την μεγαλύτερη ομοιότητα που έχει παρατηρηθεί μέχρι στιγμής.
Βήμα 2: Έστω Κ μια από τις κατηγορίες που έχουν δημιουργηθεί μέχρι στιγμής.
Βήμα 3: Έστω s η ομοιότητα του δοσμένου είδους ε με το “κέντρο” της κατηγορίας Κ.
Βήμα 4: Αν το s είναι μικρότερο από ένα ελάχιστο όριο σ (ένα “κατώφλι” — threshold στα αγγλικά), τότε
πήγαινε πίσω στο Βήμα 2.
Βήμα 5: Αλλιώς αν το s είναι μεγαλύτερο από τη μεγαλύτερη ομοιότητα που έχει παρατηρηθεί μέχρι στιγμής, τότε
Βήμα 6: σημείωσε την Κ σαν την κοντινότερη κατηγορία, και
Βήμα 7: σημείωσε το s σαν τη μεγαλύτερη ομοιότητα μέχρι στιγμής.
Βήμα 8: Αν υπάρχουν κι άλλες κατηγορίες που έχουν δημιουργηθεί ως τώρα, πήγαινε πίσω στο Βήμα 2.
Βήμα 9: Αλλιώς (εφόσον τελείωσαν οι κατηγορίες), δώσε σαν αποτέλεσμα την κοντινότερη κατηγορία που βρέθηκε όταν περάσαμε από το Βήμα 6. Κι αν δεν περάσαμε ποτέ από το Βήμα 6, τότε το αποτέλεσμα είναι: “καμία κατηγορία”.
Φυσικά, ο παραπάνω υπο-αλγόριθμος χρησιμοποιεί την ομοιότητα s όπως αυτή ορίζεται από το δεύτερο τύπο του ΓΜΠ.
Επίσης ο αλγόριθμος αυτός εξαρτάται από μια “καθολική παράμετρο”: το κατώφλι σ του βήματος 4. Λέγεται “καθολική” γιατί είναι γνωστή συνολικά στον αλγόριθμο (και στα δύο τμήματά του), και “παράμετρος” γιατί το αποτέλεσμα του αλγορίθμου (δηλαδή το πόσες και ποιες κατηγορίες θα “αντιληφθεί”) εξαρτάται από την τιμή-της. Επειδή η τιμή της παραμέτρου σ είναι συγκεκριμένη και γνωστή πριν καν ξεκινήσει ο αλγόριθμος, αυτό το γεγονός κάνει τον αλγόριθμο “δύσκαμπτο” (αγγλ.: inflexible) στο αποτέλεσμα που παράγει, οπότε το αποτέλεσμα μπορεί να μη συμφωνεί απόλυτα με τις κατηγορίες που θα έβλεπε ο μέσος άνθρωπος.
Έχουν διατυπωθεί πολλές παραλλαγές του παραπάνω αλγορίθμου, που η κάθε μία καταφέρνει να κατηγοριοποιεί κάποια δεδομένα είδη καλύτερα από κάποιες άλλες παραλλαγές. Από νοολογική άποψη, σημαντικότερες είναι εκείνες οι παραλλαγές που συμφωνούν με την κρίση των ανθρώπων (όταν αυτοί εξετάζονται στο εργαστήριο) για το ποιες είναι οι κατηγορίες.
Προέλευση του Πρώτου Νόμου
Ο Πρώτος Νόμος δεν είναι κάτι το ξεκάρφωτο, δηλαδή κάτι το οποίο εμφανίστηκε ξαφνικά μια μέρα στο νου των ανθρώπων, αλλά προϋπήρχε της ανθρώπινης νόησης. Μάλιστα η αρχέγονη μορφή-του εξακολουθεί να υπάρχει στη νόησή μας, και τα αποτελέσματά της τα αισθανόμαστε κυριολεκτικά κάθε στιγμή που έχουμε ανοιχτά τα μάτια-μας και βλέπουμε το οτιδήποτε. Ας θεωρήσουμε μια οποιαδήποτε εικόνα, όπως την παρακάτω στα αριστερά:
 |
|
Η εικόνα στ’ αριστερά δείχνει δυο παπαγαλάκια (του είδους Aratinga solstitialis). Αν όμως το καλοσκεφτούμε, αυτό το οποίο έρχεται σαν δεδομένο στον εγκέφαλο από τα μάτια δεν είναι “δυο παπαγαλάκια”, αλλά ένας τεράστιος αριθμός από χρωματισμένα σημεία. Ο αμφιβληστροειδής χιτώνας του ματιού αποτελείται από κύτταρα, τα κωνία και τα ραβδία, και σε συνθήκες φωτισμού όπως αυτός στον οποίο θα βλέπαμε τα παπαγαλάκια της φωτογραφίας, τα κωνία είναι αυτά που μεταφέρουν την πληροφορία στον εγκέφαλο. Όμως κάθε κωνίο στέλνει ένα χρώμα, δηλαδή μία κουκκίδα χρωματισμένη. (Η εικόνα στα δεξιά δείχνει σχηματικά αυτή την ιδέα, αλλά υπερβάλλοντας το μέγεθος των κουκκίδων, επομένως μικραίνοντας τον αριθμό-τους· θα πρέπει να φανταστούμε εκατομμύρια τέτοιες κουκκίδες, πιο πολλές κι από τα pixels της φωτογραφίας.) Πώς μπορεί λοιπόν ο εγκέφαλος και ανασυνθέτει το αντικείμενο “παπαγαλάκι” (δυο φορές, όπως και τα “κλαδί δέντρου” και “τοίχος”, στη φωτογραφία) από τα εκατομμύρια των χρωματισμένων κουκκίδων που λαμβάνει μέσω των κωνίων του αμφιβληστροειδούς;
Μια απάντηση στο ερώτημα αυτό δίνει ο Πρώτος Νόμος: όπως οι κουκκίδες που θεωρήσαμε νωρίτερα σε χώρο δύο διαστάσεων — όπου όμως εκεί η κάθε κουκκίδα αντιπροσώπευε μια σύνθετη έννοια, όπως “αχλάδι” — έτσι κ’ εδώ έχουμε να κάνουμε με άλλες κουκκίδες. Τώρα όμως πρόκειται κυριολεκτικά για κουκκίδες, χρωματισμένες, και τίποτ’ άλλο. Η κάθε κουκκίδα του ενός κωνίου λοιπόν έχει μια θέση στο χώρο, άρα δύο διαστάσεις (συντεταγμένες) x και y. Έχει επίσης και ένα χρώμα, που αν το αναλύσουμε θα δούμε οτι προσθέτει τρεις επιπλέον διαστάσεις: το είδος του χρώματος (κόκκινο, πράσινο, κίτρινο, κλπ), τη φωτεινότητά του (πόσο φωτεινό – άσπρο ή σκοτεινό – μαύρο τείνει να είναι), και την περιεκτικότητά του (πόσο έντονα χρωματισμένο ή ξέθωρο – γκριζωπό τείνει να είναι). Αυτές οι τρεις χρωματικές διαστάσεις μαζί με τις δύο του χώρου (x και y) μας κάνουν πέντε συνολικά διαστάσεις. Άρα στον 1ο τύπο του ΓΜΠ που δίνει την απόσταση d μεταξύ εννοιών — εδώ κυριολεκτικά κουκκίδων — πρέπει να θεωρήσουμε οτι το ν είναι ίσο με 5. Στα βάρη (τα w1, w2, w3, w4, και w5) θα πρέπει να δώσουμε σταθερές τιμές, ανάλογες της σπουδαιότητας της κάθε διάστασης (π.χ. πιθανώς το είδος του χρώματος να είναι πιο σημαντικός παράγοντας που μας κάνει να ξεχωρίζουμε κουκκίδες από τη φωτεινότητα και την περιεκτικότητα σε χρώμα). Χρησιμοποιώντας τους δύο πρώτους τύπους του ΓΜΠ, μπορούμε να υπολογίσουμε το πόσο διαφέρουν μεταξύ-τους οποιεσδήποτε δύο κουκκίδες που έρχονται από κωνία του αμφιβληστροειδούς. Με τον τρίτο τύπο, και με κάποιες ακόμα παραδοχές, μπορούμε να κατηγοριοποιήσουμε τις κουκκίδες, ώστε π.χ. όλες εκείνες που αποτελούν το κιτρινο-πορτοκαλί στήθος και το κεφάλι του πτηνού να κατατάσσονται σε μία κατηγορία· όλες εκείνες που αποτελούν τις πράσινες φτερούγες να κατατάσσονται σε άλλη κατηγορία· κ.ο.κ.
Στη συνέχεια βέβαια, έχοντας αυτές τις ομάδες (κατηγορίες) κουκκίδων, ο εγκέφαλος προχωρεί σε ανώτερου επιπέδου υπολογισμούς προκειμένου να φτάσει στην έννοια “παπαγαλάκι”. Αυτό όμως είναι κάτι που κατορθώνει ο νους του ανθρώπου. Αντίθετα, ο νους του αετού ή του γερακιού δεν θα φτάσει σε μια τόσο εξειδικευμένη έννοια όπως “παπαγαλάκι” (γιατί δεν του χρειάζεται), αλλά ίσως στη γενικότερη και απλούστερη έννοια “τροφή”. Πάντως, τόσο ο ανθρώπινος νους, όσο και εκείνος του αρκετά αναπτυγμένου (από νοητική άποψη) ζώου, ξεκινούν από το ίδιο “υπόβαθρο”: την αντίληψη αντικειμένων, φτιάχνοντας ομάδες (κατηγορίες) από τις κουκκίδες που στέλνουν σαν σήμα στον εγκέφαλο τα κύτταρα του αμφιβληστροειδούς του ματιού.
Αυτή λοιπόν η παρατήρηση μας δίνει μια υπόδειξη για το από πού μπορεί να προέρχεται ο Πρώτος Νόμος. Αν πάμε αρκούντως πίσω στο παρελθόν, θα βρούμε μόνο είδη ζώων που μπορούσαν να εφαρμόσουν τον Πρώτο Νόμο στην κυριολεκτική-του μορφή, δηλαδή σαν ένα μέσο αντίληψης αντικειμένων, βλέποντας τις ομάδες που σχηματίζουν οι κουκκίδες των ματιών. Τα αντικείμενα αυτά συσχετίζονται με πολύ απλές έννοιες στους νους των ζώων αυτών, όπως “τροφή”, “κίνδυνος”, κλπ. Καθώς τα ζώα εξελίσσονται, οι απλές έννοιες που ενεργοποιούν τα αντικείμενα αρχίζουν να ξεχωρίζουν σε πιο σύνθετες. Π.χ. στο μυαλό ενός πιθήκου ή ενός λύκου, το άτομο που ανήκει στην οικογένεια είναι διαφορετική έννοια από το άτομο μιας άλλης φυλής· το ίδιο ισχύει και για διάφορα είδη τροφής, τα οποία διαχωρίζουν τα πιο νοήμονα από τα ζώα. Με τα προγονικά είδη του ανθρώπου (τους αυστραλοπίθηκους, και τα είδη του γένους Άνθρωπος), ο διαχωρισμός αυτός σε κατηγορίες έφτασε σε υψηλά επίπεδα πολυπλοκότητας. Αυτό που είναι σίγουρο είναι οτι το δικό-μας είδος (Άνθρωπος ο σοφός) μπορεί να διαχωρίζει υποκατηγορίες υποκατηγοριών, και να χρησιμοποιεί σαν “κουκκίδα” μια ολόκληρη έννοια (όπως περιγράφει το ΓΜΠ), εκεί που ο νους των νοητικά απλούστερων ζώων μπορεί να χειριστεί μόνο τις κουκκίδες στην κυριολεξία, και τίποτε παραπάνω. Αυτό το οποίο ήταν απλή αντίληψη αντικειμένων στα νοητικά απλούστερα ζώα, μέσω της διαδικασίας της εξέλιξης μετεξελίχθηκε σε ικανότητα κατηγοριοποίησης εννοιών, ακόμα και αφηρημένων, στο δικό-μας είδος. Αυτό φυσικά είναι μια εικασία, που μένει να αποδειχτεί. Αν όμως είναι σωστή, μας δείχνει οτι ο Πρώτος Νόμος είναι εκείνη η ικανότητα μέσω της οποίας ο νους διακρίνει αντικείμενα στον κόσμο — είτε φυσικά και συγκεκριμένα, είτε νοητά και αφηρημένα.
Ένα φιλοσοφικό ερώτημα: τα αντικείμενα υπάρχουν αντικειμενικά, ή τα κατασκευάζει υποκειμενικά ο νους-μας;
Ένα ερώτημα που τίθεται από φιλοσόφους που ασχολούνται με τη φιλοσοφία του πνεύματος είναι το εξής: τα αντικείμενα υπάρχουν πράγματι στον κόσμο που μας περιβάλλει, ή τα δημιουργεί ο νους του ανθρώπου;
Παρόλο που το ερώτημα είναι φιλοσοφικό, άρα εκτός των ορίων της επιστήμης, βάσει των παραπάνω μπορούμε να υποπτευθούμε ποια πρέπει να είναι η σωστή απάντηση.
![]() Αν
τα αντικείμενα είναι απλώς δημιουργήματα του ανθρώπινου νου, τότε μένει
αναπάντητο το ερώτημα του γιατί τα δημιουργεί ο νους-μας. Η ικανότητα αυτή μοιάζει αυθαίρετη, “ξεκάρφωτη”, σαν
να μας ήρθε από το πουθενά, και να
υπάρχει μόνο για να υπάρχει.
Αν
τα αντικείμενα είναι απλώς δημιουργήματα του ανθρώπινου νου, τότε μένει
αναπάντητο το ερώτημα του γιατί τα δημιουργεί ο νους-μας. Η ικανότητα αυτή μοιάζει αυθαίρετη, “ξεκάρφωτη”, σαν
να μας ήρθε από το πουθενά, και να
υπάρχει μόνο για να υπάρχει.
![]() Αντίθετα, αν τα αντικείμενα υπάρχουν αντικειμενικά στον κόσμο (δηλ.
είναι ιδιότητα του σύμπαντος στο οποίο υπάρχουμε), τότε έχουμε
μια εξήγηση για το γιατί τα αντιλαμβάνεται ένας νους. Η εξήγηση είναι
βιολογικής-εξελικτικής φύσης: επειδή υπάρχουν αντικείμενα στον
κόσμο, γιαυτό τα ζώα εξελίχθηκαν ώστε να ανταποκρίνονται στην
ιδιότητα αυτή του περιβάλλοντός τους, δηλαδή στο να αντιλαμβάνονται τα
φυσικά αντικείμενα και να δρουν με τρόπους που τους επιτρέπουν να
πολλαπλασιάζουν τα γονίδιά τους (να επιβιώνουν). Π.χ. το ζώο που μπορεί
να αντιληφθεί οπτικά ένα αντικείμενο σαν “τροφή” ή “εμπόδιο” έχει πιο πολλές
πιθανότητες επιβίωσης από άλλο ζώο με ακριβώς τα ίδια χαρακτηριστικά
όπως το πρώτο, αλλά χωρίς τέτοια αντιληπτική ικανότητα. Όσο πιο
οξυδερκής είναι αυτή η ικανότητα αντίληψης αντικειμένων, τόσο πιο καλά
θα πρέπει να επιβιώνει το ζώο. Επομένως πρώτα έρχεται η ύπαρξη
αντικειμένων στον κόσμο, και έπειτα οι νόες των ζώων και του ανθρώπου,
που εξελίχθηκαν ώστε να εκμεταλλεύονται προς το συμφέρον-τους (για την
επιβίωσή τους) την ιδιότητα αυτή του κόσμου.
Αντίθετα, αν τα αντικείμενα υπάρχουν αντικειμενικά στον κόσμο (δηλ.
είναι ιδιότητα του σύμπαντος στο οποίο υπάρχουμε), τότε έχουμε
μια εξήγηση για το γιατί τα αντιλαμβάνεται ένας νους. Η εξήγηση είναι
βιολογικής-εξελικτικής φύσης: επειδή υπάρχουν αντικείμενα στον
κόσμο, γιαυτό τα ζώα εξελίχθηκαν ώστε να ανταποκρίνονται στην
ιδιότητα αυτή του περιβάλλοντός τους, δηλαδή στο να αντιλαμβάνονται τα
φυσικά αντικείμενα και να δρουν με τρόπους που τους επιτρέπουν να
πολλαπλασιάζουν τα γονίδιά τους (να επιβιώνουν). Π.χ. το ζώο που μπορεί
να αντιληφθεί οπτικά ένα αντικείμενο σαν “τροφή” ή “εμπόδιο” έχει πιο πολλές
πιθανότητες επιβίωσης από άλλο ζώο με ακριβώς τα ίδια χαρακτηριστικά
όπως το πρώτο, αλλά χωρίς τέτοια αντιληπτική ικανότητα. Όσο πιο
οξυδερκής είναι αυτή η ικανότητα αντίληψης αντικειμένων, τόσο πιο καλά
θα πρέπει να επιβιώνει το ζώο. Επομένως πρώτα έρχεται η ύπαρξη
αντικειμένων στον κόσμο, και έπειτα οι νόες των ζώων και του ανθρώπου,
που εξελίχθηκαν ώστε να εκμεταλλεύονται προς το συμφέρον-τους (για την
επιβίωσή τους) την ιδιότητα αυτή του κόσμου.
Η δεύτερη απάντηση κάνει επίσης την πρόβλεψη οτι αν υπάρχουν νοήμονες εξωγήινοι που να δημιουργήθηκαν μέσω φυσικής επιλογής όπως εμείς και να έχουν την αίσθηση της όρασης, κι αυτοί θα πρέπει ν’ αντιλαμβάνονται τα ίδια αντικείμενα στο σύμπαν όπως κ’ εμείς. (Βέβαια αν δεν υπάρχουν τέτοιοι εξωγήινοι, η πρόβλεψη αυτή μένει ανεπιβεβαίωτη.) Περί προβλέψεων θα μάθουμε σχετικά στον Τρίτο Νόμο. Όσο για το γιατί η δεύτερη εξήγηση (περί αντικειμενικότητας της ύπαρξης των αντικειμένων) μας φαίνεται πιο ελκυστική, αυτό θα το καταλάβουμε στη συζήτηση για τον Τέταρτο Νόμο.
Δεύτερος Νόμος: Απομόνωση Πυρήνα
Το τί σημαίνει (και πώς συμβαίνει υποσυνείδητα) η απομόνωση του πυρήνα μιας έννοιας θα το καταλάβουμε εξετάζοντας το φαινόμενο της αναλογίας.
Τί είναι μια αναλογία
Ας δούμε το παρακάτω παράδειγμα αυθόρμητης αναλογίας, που αφηγείται ο D. R. Hofstadter στο βιβλίο-του «Ρευστές έννοιες και δημιουργικές αναλογίες» (“Fluid Concepts and Creative Analogies”):
«Η κόρη-μου η Μόνικα, που ήταν τότε λίγο παραπάνω από ενός έτους, καθόταν στο πάτωμα του δωματίου-της, πατώντας το κουμπί ON–OFF ενός Ξεσκονισίφουνα (μιας χειροκίνητης ηλεκτρικής σκούπας που δούλευε με μπαταρίες), που το λάτρευε λόγω του θορύβου που έκανε. Κάποια στιγμή πρόσεξε ένα κουμπί με διαφορετικό σχήμα, σε διαφορετικό σημείο του Ξεσκονισίφουνα, και φυσικά προσπάθησε να το πατήσει. Δεν έγινε τίποτα. Αφού προσπάθησε αρκετές φορές, τελικά το παράτησε. Ο λόγος που αυτό το κουμπί δεν έκανε τίποτα ήταν οτι άνοιγε το καπάκι που συγκρατούσε τη σακούλα των απορριμμάτων μέσα στη συσκευή, και πατώντας-το δεν γίνεται τίποτα. Πρέπει να το σύρει κανείς, αλλά και τότε, το μόνο που συμβαίνει είναι οτι το καπάκι πετάγεται ανοίγοντας. Αυτό ξεπερνούσε κατά πολύ τον ορίζοντά της για κατανόηση, όχι όμως και τον αντίστοιχο για απογοήτευση.
Όταν είδα τη Μόνικα να προσπαθεί μ’ εκείνο το δεύτερο κουμπί και να βαλτώνει, πήγα κοντά-της και της έδειξα τί κάνει. Ξαφνικά, εντελώς σαν από το πουθενά, μια εμπειρία της παιδικής-μου ηλικίας άστραψε στη μνήμη-μου. Όταν ήμουν μικρός, μου άρεζαν πολύ τα μαθηματικά. Κάτι που με ενθουσίαζε ιδιαίτερα ήταν η πράξη της ύψωσης σε δύναμη. Έφτιαχνα πίνακες τον ένα μετά τον άλλον από τετράγωνα, κύβους, και μεγαλύτερες δυνάμεις πολλών ακεραίων αριθμών, συνέκρινα τ’ αποτελέσματα, και μελετούσα τα επαναλαμβανόμενα μοτίβα. Ήμουν καταμαγεμένος. Μια μέρα, όταν θα ’μουν γύρω στα οκτώ, έτυχε να δω μια από τις δημοσιεύσεις φυσικής του πατέρα-μου(*) σε κάτι χαρτιά που κείτονταν στο τραπέζι του σπιτιού-μας, και έριξα μια ματιά στις εξισώσεις. Φυσικά, ήσαν εντελώς ακατανόητες για μένα, αλλά πρόσεξα ένα πολύ κοινό χαρακτηριστικό-τους: την άφθονη χρήση δεικτών. Βέβαια γνώριζα οτι οι εκθέτες εκπροσωπούν την απείρου κάλλους και βάθους πράξη της ύψωσης σε δύναμη, οπότε βιάστηκα να συμπεράνω οτι και οι δείκτες, αφού μοιάζουν τόσο πολύ με τους εκθέτες, θα πρέπει κι αυτοί να εκπροσωπούν κάποια μυστηριώδη και βαθιά μαθηματική πράξη.»
«Έτσι, ρώτησα τον πατέρα-μου. Προς μεγάλη-μου απογοήτευση, μου είπε οτι οι δείκτες χρησιμοποιούνται απλώς για να ξεχωρίζουμε τη μια μεταβλητή από την άλλη, κι οτι καμιά απολύτως μαθηματική πράξη δεν συμβολίζεται βάζοντας π.χ. το δείκτη 3 στο γράμμα x. Έτσι σβήστηκαν τα παιδικά-μου όνειρα ν’ ανακαλύψω κάποιο χαμένο μαθηματικό θησαυρό.»
Και ο Hofstadter συνεχίζει:
«Αυτή ήταν η ανάμνηση που μου πέρασε απ’ το μυαλό όταν η μικρή Μόνικα απέτυχε να κάνει ένα νέο θόρυβο πατώντας το δεύτερο κουμπί του Ξεσκονισίφουνα. Η Μόνικα ήταν εγώ, εγώ ήμουν ο πατέρας-μου, το πρώτο κουμπί ήταν οι εκθέτες, το δεύτερο κουμπί οι δείκτες, ο θόρυβος ήταν η μαγεία της ύψωσης σε δύναμη, η απουσία θορύβου ήταν η απουσία μαθηματικής πράξης με τους δείκτες... Όταν το σκέφτεσαι ακούγεται πολύ λογικό — τα δύο γεγονότα αντιστοιχούν το ένα στο άλλο τέλεια: πατέρες, παιδιά, απογοήτευση — τα πάντα. Αλλά πώς συνέβη η ανάκληση του παλιού επεισοδίου; Πώς αποθήκευσε το οκτάχρονο αγόρι εκείνο το επεισόδιο; Πώς το ξετρύπωσε και το ανέσυρε ο ενήλικος, κάπου σαράντα χρόνια αργότερα, χάρη στο συμβάν με τη μικρή-του κόρη;»
Το παραπάνω είναι ένα παράδειγμα αναλογίας, και μάλιστα εκπληκτικής από την άποψη της αφαίρεσης και του τρόπου με τον οποίο εμφανίστηκε στο νου του αφηγητή. Έχουμε δύο καταστάσεις που φαινομενικά δεν έχουν τίποτε το κοινό· όμως με μια πιο προσεκτική εξέταση, βρίσκουμε οτι εφαρμόζουν τέλεια η μια στην άλλη, εφόσον εστιάσουμε την προσοχή-μας στο ουσιώδες, στον κοινό πυρήνα των δύο καταστάσεων. Ιδού ο κοινός — αλλά αφηρημένος — “πυρήνας”:
| Ένα παιδί ψυχαγωγείται με ένα χαρακτηριστικό ενός αντικειμένου. Ξαφνικά, το παιδί ανακαλύπτει και δεύτερο χαρακτηριστικό στο αντικείμενο αυτό, που του φαίνεται παρόμοιο με το πρώτο. Προσπαθεί να παίξει και με το δεύτερο όπως έπαιζε με το πρώτο, αλλά αποτυγχάνει. Ο πατέρας-του του δίνει να καταλάβει οτι αυτό το δεύτερο χαρακτηριστικό δεν κάνει και τίποτα το σπουδαίο, και είναι εντελώς διαφορετικό από το πρώτο παρά τη φαινομενική ομοιότητα. Το παιδί απογοητεύεται. |
Ο παραπάνω πυρήνας εφαρμόζει καί στις δυο καταστάσεις αυτούσιος. Το μεγάλο ερώτημα όμως είναι, πώς θυμήθηκε ο Hofstadter το παλιό επεισόδιο δοσμένου αυτού που συνέβη «κάπου σαράντα χρόνια αργότερα»;
Απαντώντας στο παραπάνω ερώτημα, θα απαντηθεί ταυτόχρονα και ένα “μετα-ερώτημα” που μπορεί να έχει τώρα ο αναγνώστης: «Ποια είναι η σπουδαιότητα του παραπάνω φαινομένου, και τί σχέση έχει με το “Δεύτερο Νόμο” της νοολογίας;»
Αυτό που συνέβη στο νου του Hofstadter — αλλά με “θεαματικό” τρόπο — συμβαίνει καθημερινά σε όλους-μας, αλλά με τετριμμένο τρόπο. Μας συμβαίνει κυριολεκτικά κάθε ώρα και στιγμή που έχουμε ανοιχτά τα μάτια-μας και βλέπουμε το οτιδήποτε. Για να το καταλάβουμε αυτό, ας εξετάσουμε την παρακάτω εικόνα:
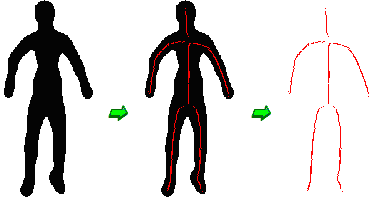
Στ’ αριστερά βλέπουμε μια ανθρώπινη φιγούρα. Στο μέσον, κάποια “κεντρικά” σημεία έχουν μετατραπεί σε κόκκινα, σχηματίζοντας ένα είδος “σκελετού” της φιγούρας. Στα δεξιά, τα κεντρικά αυτά σημεία έχουν απομονωθεί.
Τα κόκκινα κεντρικά σημεία δεν είναι αυθαίρετα, αλλά κατασκευάστηκαν με ένα μηχανικό τρόπο (μέσω αλγορίθμου), ο οποίος αφαιρεί τα σημεία της περιφέρειας της φιγούρας, και μετά πάλι της νέας περιφέρειας, και ούτω καθεξής, μεχρι να φτάσει σε σημεία που δεν μπορούν να αφαιρεθούν πια, γιατί ανήκουν σε περιφέρεια κι από τις δυο μεριές-τους. Αυτά είναι τα κόκκινα κεντρικά σημεία. Τί σχέση έχει όμως αυτή η κατασκευή του “σκελετού” — που θα μπορούσαμε να τον πούμε και “πυρήνα της φιγούρας” — με την αναλογία του Hofstadter;
Καί στις δυο περιπτώσεις ο μηχανισμός είναι ο ίδιος, και μπορούμε να τον ονομάσουμε “απομόνωση πυρήνα”:
Στην περίπτωση της φιγούρας, κάνουμε (ή εμείς ή ένας υπολογιστής) μια διαδοχική αφαίρεση των εξωτερικών σημείων, μέχρι να φτάσουμε στα “εσωτερικότερα δυνατά”, σ’ αυτά που αν τα αφαιρούσαμε δεν θα έμενε πια τίποτα.
Στην περίπτωση της αναλογίας του Hofstadter, μπορούμε επίσης να κάνουμε μια αφαίρεση επουσιωδών στοιχείων: π.χ. τί χρώμα στυλό χρησιμοποιούσε ο οκταετής Hofstadter, με πόσα διαφορετικά παραδείγματα εκθετών διασκέδασε, σε ποια πόλη βρισκόταν όταν έπαιζε το παιχνίδι των εκθετών, τί καιρό έκανε όταν συνέβη το επεισόδιο των δεικτών, κλπ. Αφαιρώντας όλα αυτά τα “περιφερειακά”, καταλήγουμε στον αφηρημένο “πυρήνα”, όπως περιγράφηκε λίγο παραπάνω.
Έχοντας τον πυρήνα, μπορούμε να κάνουμε μια αναλογία. Στην περίπτωση του Hofstadter, είδαμε ποια είναι η αναλογία. Ας δούμε λοιπόν και μια “αναλογία” στην περίπτωση της ανθρώπινης φιγούρας:
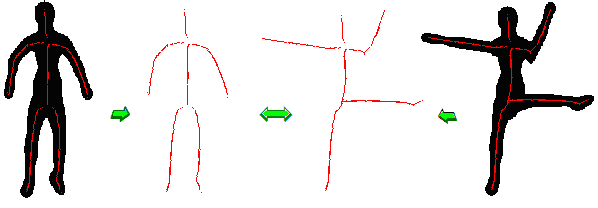
Η αριστερή φιγούρα είναι η ίδια όπως και προηγουμένως. Η δεξιά είναι προφανώς διαφορετική, αλλά στα αριστερά-της φαίνεται ο πυρήνας-της απομονωμένος. Συγκρίνοντας τους δύο πυρήνες βλέπουμε οτι τα μέρη-τους αντιστοιχούν το ένα στο άλλο: “κεφάλι” με “κεφάλι”, κορμός με κορμό, και άκρα με άκρα. Έτσι, κάνοντας μια απλή σύγκριση των δύο πυρήνων, μπορούμε να πούμε οτι οι δυο φιγούρες είναι στην ουσία ίδιες, δηλαδή “μια ανθρώπινη φιγούρα”, ανεξάρτητα από το πώς είναι τοποθετημένα τα μέλη-της στο χώρο. Μπορεί να υποθέσει κανείς οτι το ίδιο θα συμπεραίναμε και χωρίς την απομόνωση του πυρήνα, συγκρίνοντας κατευθείαν τα μαύρα σημεία-τους. Όμως όχι μόνο αυτό είναι πιο δύσκολο, αλλά θα μπορούσαν τα επουσιώδη σημεία (της άλω) να είναι πιο πολλά και πιο πολύπλοκα· π.χ. θα μπορούσε η φιγούρα στα δεξιά να είναι φωτογραφικά πιο ρεαλιστική, και να παριστάνει γυναίκα αντί για άντρα. Ας φανταστούμε λοιπόν τώρα έναν άντρα στ’ αριστερά, ντυμένο μόνο με μπλε μαγιό, και μια γυναίκα στα δεξιά, ντυμένη με κίτρινο αδιάβροχο που φτάνει μέχρι τη μέση, και μαύρο τζιν πανταλόνι. Πώς ταυτοποιούμε τις δύο εικόνες και λέμε οτι πρόκειται για “άνθρωπο” γενικά; Μια θεμελιώδης διαδικασία (χωρίς να είναι η μόνη στο παράδειγμα αυτό) είναι οτι αντιλαμβανόμαστε τον πυρήνα των δύο εικόνων, και διαπιστώνουμε οτι οι πυρήνες είναι ίδιοι (έχουν την ίδια δομή). Το χρώμα του μαγιό ή του αδιάβροχου, ή το αν υπάρχει πανταλόνι και είναι τζιν, είναι πράγματα επουσιώδη, που αν τους δίναμε προσοχή θα μας αποσπούσαν πολύτιμο χρόνο υπολογισμού και θα αργούσαμε να καταλάβουμε οτι έχουμε “άνθρωπο” και στις δύο περιπτώσεις.
Το ίδιο γίνεται και όταν βλέπουμε ένα οποιοδήποτε αντικείμενο. Έστω οτι βλέπουμε π.χ. ένα στυλό με καπάκι, που δεν έχουμε δει ποτέ πριν. Πώς αντιλαμβανόμαστε το αντικείμενο αυτό σαν “στυλό με καπάκι”, και όχι σαν “μακρουλό αντικείμενο, περίπου είκοσι εκατοστών, και πάχους μισού εκατοστού, κίτρινου χρώματος, πλαστικής ύλης, με ένα μπλε εξόγκωμα στο ένα άκρο...” κλπ; Αυτό που κάνουμε είναι οτι αφαιρούμε (νοητά) όλα αυτά τα επουσιώδη χαρακτηριστικά που μόλις αναφέρθηκαν, και διατηρούμε τον πυρήνα (που είναι λίγο πιο αφηρημένης μορφής από εκείνον της ανθρώπινης φιγούρας του προηγούμενου παραδείγματος), τον οποίο “ταιριάζουμε” με τον πυρήνα “στυλό με καπάκι” που έχουμε αποθηκεύσει στη μνήμη-μας, χάρη στα διάφορα στυλό με καπάκια που έχουμε δει στη μέχρι τώρα ζωή-μας. Κάνουμε λοιπόν μια αναλογία, αλλά τετριμμένης μορφής, μεταξύ του στυλό που βλέπουμε μπροστά-μας, και της έννοιας “στυλό με καπάκι” που έχουμε στη μνήμη-μας.
Το ίδιο συνέβη και στο επεισόδιο που περιέγραψε ο Hofstadter: έκανε μια αναλογία μεταξύ του επεισοδίου που έβλεπε εκείνη την ώρα (με την κόρη-του να παίζει, κλπ.), και του επεισοδίου που είχε στη μνήμη-του από την παιδική-του ηλικία. Η αναλογία δεν θα μπορούσε να παρατηρηθεί αν δεν είχε ήδη αποθηκευτεί ο πυρήνας του παλιού επεισοδίου μαζί με την άλω, δηλ. τα πιο περιφερειακά στοιχεία-του.
Αυτή είναι μια πολύ σημαντική παρατήρηση: όποτε βλέπουμε ένα αντικείμενο, ή παρατηρούμε ένα γεγονός, αποθηκεύουμε στη μνήμη όχι μόνο το αντικείμενο ή το γεγονός καθαυτό, αλλά και τον πυρήνα-του, τον οποίο απομονώνουμε υποσυνείδητα.
Αλλά πώς τα καταφέρνουμε να “ταιριάξουμε” τους δύο πυρήνες, τον παλιό — τον αποθηκευμένο στη μνήμη — και το νέο; Δηλαδή, υπάρχει το εξής ερώτημα: έστω οτι ο παλιός πυρήνας είναι αποθηκευμένος κάπου στη μνήμη· όταν τώρα έρχεται ο νέος πυρήνας, πώς τα καταφέρνουμε και εντοπίζουμε τον παλιό πυρήνα μέσα στον αχανή χώρο της ανθρώπινης μνήμης; Η μνήμη έχει αποθηκευένο ένα τεράστιο πλήθος πληροφοριών. Πώς λοιπόν, μέσα στις δεκάδες, ή εκατοντάδες χιλιάδες πληροφορίες (με τους πυρήνες-τους η κάθε μία), εντοπίζεται ακριβώς ο παλιός πυρήνας που τυχαίνει να μοιάζει με τον τωρινό;
Η εντόπιση γίνεται μέσω του Πρώτου Νόμου, της κατηγοριοποίησης. Ο νέος πυρήνας είναι κι αυτός ένα δεδομένο, μια “κουκκίδα” όπως εκείνες που κατηγοριοποιούσαμε στην προηγούμενη ενότητα. Όταν έρχεται στην αντίληψή μας η “κουκκίδα” αυτή, τοποθετείται “κοντά” σ’ εκείνη που αντιστοιχεί στον παλιό πυρήνα, γιατί η διαφορά-τους d είναι μικρή, και άρα η ομοιότητά τους s μεγάλη. Η “τοποθέτηση” αυτή γίνεται αυτόματα. Δεν πρόκειται για κάποιον ειδικό μηχανισμό, αλλά γι’ αυτόν που περιγράφεται από τον Πρώτο Νόμο.(*)
Οι δύο πυρήνες μπορούν να είναι “κοντά” ο ένας στον άλλον γιατί έχουν λίγες διαστάσεις, δηλαδή το ν στους τύπους που μας δίνουν τη διαφορά d και την ομοιότητα s είναι μικρό. Αν είχαμε να κάνουμε όχι απλώς με τους πυρήνες, αλλά με όλα τα χαρακτηριστικά, τότε το ν θα ήταν μεγάλο, οπότε η διαφορά d θα εξαρτιόταν από πολλά ανόμοια μεταξύ-τους χαρακτηριστικά και ο υπολογισμός-της θα έδινε τιμή όχι ιδιαίτερα μικρή· αντίστοιχα, η ομοιότητα δεν θα ήταν ιδιαίτερα μεγάλη. Το αποτέλεσμα θα ήταν οτι δεν θα παρατηρούσαμε την ομοιότητα, καθώς ο νέος πυρήνας δεν θα ενεργοποιούσε τον παλιό. Αυτός είναι ο λόγος που είναι απαραίτητη η εξαγωγή του πυρήνα, της “κεντρικής ιδέας” κάθε αντικειμένου και κάθε γεγονότος που υποπίπτει στην αντίληψή μας.
Κάνοντας τη σύνδεση με όσα αναφέρθηκαν στην αρχή, ας θυμηθούμε πάλι τα “τρίγωνα του Πλάτωνα”:


Στο άνω μέρος είναι τα τρίγωνα που βλέπουμε στο φυσικό κόσμο. Στο κάτω μέρος είναι αυτό που σχηματίζεται στο νου-μας: η Πλατωνική ιδέα “τρίγωνο”, ο πυρήνας της έννοιας. Αντίστοιχα, σχηματίζουμε Πλατωνικές ιδέες (πυρήνες) για οποιαδήποτε έννοια. Έχουμε π.χ. στη μνήμη-μας την Πλατωνική ιδέα “στυλό με καπάκι”, δηλαδή τον πυρήνα της έννοιας αυτής, που τον απομονώσαμε από διάφορα παραδείγματα τέτοιων αντικειμένων. Με τον τρόπο αυτόν αναγνωρίζουμε αντικείμενα σαν “ίδια” (δηλαδή παρόμοια), είτε πρόκειται για απτά φυσικά αντικείμενα όπως στυλό, είτε για συνταγές μαγειρικής με παρόμοια εκτέλεση, είτε για μουσικές μελωδίες που μας θυμίζουν η μια την άλλη, είτε για λογοτεχνικά έργα που έχουν παρόμοιο σενάριο, είτε για ολόκληρα επεισόδια όπως εκείνα του Hofstadter.
Σαν ένα άλλο παράδειγμα απομόνωσης πυρήνα, ας σκεφτούμε το τί ειπώθηκε στην ενότητα αυτή σχετικά με το Δεύτερο Νόμο. Ο αναγνώστης αποκλείεται να θυμάται τις συγκεκριμένες λέξεις και προτάσεις που χρησιμοποιήθηκαν, ούτε το πού έγινε χρήση πλάγιας γραφής, ή πού τοποθετήθηκαν τα διαγράμματα, γιατί όλα αυτά ανήκουν στις περιφερειακές λεπτομέρειες, στην “άλω”. Αυτό που μένει στο νου του αναγνώστη είναι το νόημα, η κεντρική ιδέα, ο πυρήνας. Όσο πιο συγκεκριμένη η πληροφορία, τόσο πιο γρήγορα ξεχνιέται, ενώ όσο πιο γενική και αφηρημένη, τόσο πιο πολύ συγκρατείται στη μνήμη.
Άλλο παράδειγμα, οικείο σε όλους-μας: τη μια μέρα, κάνουμε τη σκέψη: «Αύριο πρέπει να πάω στην Τράπεζα να κάνω μια ανάληψη του ποσού που πρέπει να στείλω για τη συνδρομή του περιοδικού.» Όταν έρχεται η επόμενη μέρα, μπορεί αυτό που θυμόμαστε να είναι: «Σήμερα ήταν να πάω στην Τράπεζα για να κάνω κάτι, αλλά τί ήταν αυτό που θα έκανα;» Η “λεπτομέρεια” «ανάληψη ... για τη συνδρομή του περιοδικού» έχει χαθεί προσωρινά από τη δομή της ιδέας, και έχουν μείνει μόνο τα πιο γενικά χαρακτηριστικά. Σε άλλη περίπτωση, μπορεί το μόνο που μας έχει μείνει στη μνήμη να είναι: «Σήμερα είχα να θυμηθώ να κάνω κάτι, αλλά τί ήταν αυτό;» Εδώ και η πληροφορία «να πάω στην Τράπεζα» έχει προσωρινά χαθεί, και έχει μείνει ο πυρήνας μόνο της γενικής ιδέας «κάτι έπρεπε να θυμηθώ να κάνω σήμερα». Χωρίς παραπέρα βοήθεια (π.χ. από μια ατζέντα όπου είναι σημειωμένο το γεγονός, ή από άλλο γεγονός που θα μας θυμίσει το πρώτο), μένουμε μόνο με τον πυρήνα, που είναι μάλλον άχρηστος στην περίπτωση αυτή.
Η διαδικασία απομόνωσης του πυρήνα μέσω της σταδιακής απαλοιφής των περιφερειακών στοιχείων, και η συνακόλουθη χρήση του πυρήνα προκειμένου να ανακληθούν έννοιες από τη μνήμη είναι ο Δεύτερος Νόμος.
Τρίτος Νόμος: Συμπλήρωση Μοτίβου
Ας υποθέσουμε οτι πηγαίνουμε να ζήσουμε σε περιοχές με εύκρατο κλίμα των βόρειων Ηνωμένων Πολιτειών, στις λεγόμενες “Μεσοδυτικές Πολιτείες” (“Midwest”). Καθώς ζούμε εκεί, κάθε χρόνο παρατηρούμε το εξής φαινόμενο: στις αρχές του φθινοπώρου τα δέντρα έχουν ακόμα πράσινο φύλλωμα, όπως και το καλοκαίρι· όμως γύρω στον Οκτώβριο ή Νοέμβριο, μέσα σε δύο ή τρεις μέρες το πολύ, τα φύλλα όλων των φυλλοβόλων δέντρων απότομα κιτρινίζουν ή κοκκινίζουν (βλ. φωτογραφίες).
 |
 |
 |
 |
Μπορεί να παραξενευτούμε απ’ το φαινόμενο αυτό: πώς “ξέρουν” τα φύλλα οτι πρέπει ν’ αλλάξουν χρώμα τόσο ξαφνικά; Πώς γίνεται να “συνεννοούνται” δέντρα τόσο διαφορετικών ειδών, και για ποιο λόγο;
Καθώς το φαινόμενο επαναλαμβάνεται χρόνο με το χρόνο, μπορεί ν’ αρχίσουμε να υποπτευόμαστε τί συμβαίνει: όσο ο καιρός είναι ήπιος, τα φύλλα παραμένουν πράσινα· μόλις όμως κάνει ένα δυνατό κρύο και η θερμοκρασία πέσει κοντά στους 0° Κελσίου, μέσα στις επόμενες λίγες μέρες τα φύλλα αλλάζουν χρώμα — προφανώς λόγω κάποιων χημικών διεργασιών που συντελούνται μέσα-τους από την πτώση της θερμοκρασίας. Αυτό που έχουμε κάνει είναι οτι παρατηρήσαμε ένα επαναλαμβανόμενο μοτίβο: το δυνατό κρύο επιφέρει αλλαγή χρωματισμού στη χλωρίδα. Επομένως το επόμενο έτος, όταν πιάσει ένα δυνατό κρύο το φθινόπωρο, μπορούμε να προβλέψουμε οτι τις επόμενες μέρες τα φύλλα θα αλλάξουν χρώμα.
Βέβαια η παρατήρηση ενός μοτίβου όπως το παραπάνω και η συνεπαγόμενη πρόβλεψη δεν πρόκειται να έχουν κάποια σημαντική επίπτωση στη ζωή-μας. (Το πολύ-πολύ, βλέποντας το κρύο, να οργανώσουμε ένα πικ-νικ στην εξοχή για να απολαύσουμε τα λαμπρά χρώματα της φύσης.) Όμως η ικανότητα για τέτοιου είδους παρατηρήσεις και προβλέψεις έπαιξε σημαντικό ρόλο στην επιβίωση του ανθρώπου. Κάποτε π.χ. οι άνθρωποι ίσως παρατήρησαν οτι μια ξαφνική ζέστη νωρίς την άνοιξη έχει σαν αποτέλεσμα το λιώσιμο του χιονιού στα βουνά, πράγμα που προκαλεί πλημμύρα στο γειτονικό ποτάμι. Η πρόβλεψη οτι «αφού κάνει ζέστη μπορεί να έχουμε πλημμύρα πάλι, άρα ας πάρουμε τα μέτρα-μας» θα έκανε τη διαφορά μεταξύ ζωής και θανάτου.
|
Αν το καλοσκεφτούμε, ολόκληρο το οικοδόμημα της επιστήμης στηρίζεται στην παρατήρηση επαναλαμβανόμενων μοτίβων, και στη συνεπαγόμενη πρόβλεψη που μπορεί να γίνει βάσει των προηγούμενων παρατηρήσεων. Π.χ., η πρόβλεψη των εκλείψεων του Ήλιου ή της Σελήνης βασίζεται στην επανάληψη λόγω της περιοδικότητας της κίνησης των ουρανίων σωμάτων· η πρόβλεψη του 19ου αιώνα οτι θα έπρεπε να υπάρχει ένα χημικό στοιχείο με ιδιότητες παρόμοιες με αυτές του ιωδίου (και των άλλων αλογόνων, δηλαδή ένα νέο αλογόνο), βασίστηκε στην παρατήρηση της περιοδικότητας των ιδιοτήτων των χημικών στοιχείων (και όντως το 1940 ανακαλύφθηκε ένα τέτοιο στοιχείο: το άστατο, ή αστάτιο)· η πρόβλεψη οτι ο κομήτης του Χάλλεϋ θα επισκεπτόταν τη γειτονιά της Γης το 1986, όπως και οτι θα την ξαναεπισκεφτεί το 2061, βασίστηκε στις προηγούμενες περιοδικές επισκέψεις του κομήτη (και ακόμα και η ταυτοποίησή του το 1705 από τον Edmond Halley [Έντμοντ Χώλλυ, ή “Χάλλεϋ” όπως έχει επικρατήσει στα ελληνικά] σαν το ίδιο ουράνιο σώμα που επισκέπτεται τη Γη κάθε 75 με 76 χρόνια έγινε δυνατή λόγω του επαναλαμβανόμενου μοτίβου των επισκέψεών του). |
 Η τροχιά του κομήτη του Χάλλεϋ |
Όμως η περιοδικότητα δεν είναι απαραίτητη για να γίνει μια πρόβλεψη. Μπορεί η πρόβλεψη να είναι στατιστικής φύσης, όπως αυτές που κάνουν οι μετεωρολόγοι για τον καιρό των επόμενων ημερών, ή οι οικονομολόγοι για την ισοτιμία ενός νομίσματος.
Ισοτιμία ευρώ με γιεν Ιαπωνίας την περίοδο 2005 – 2007
Τέτοιες προβλέψεις μπορεί να μην είναι απόλυτες, λόγω της αστάθειας των συστημάτων (καιρός, οικονομική συγκυρία, κλπ), αλλά από πιθανοθεωρητική άποψη είναι απόλυτα δικαιολογημένες.(*) Άλλωστε και η πρόβλεψη οτι «εφόσον κάνει ξαφνική ζέστη μπορεί να έχουμε πλημμύρα τις επόμενες μέρες» είναι κι αυτή πιθανοθεωρητικής φύσης.
Όλα τα παραπάνω παραδείγματα ήταν λίγο-πολύ σχετιζόμενα με την ιδέα της “επιστημονικής πρόβλεψης” — ακόμα κι αν πρόκειται για την πρόβλεψη της πλημμύρας από τον προϊστορικό άνθρωπο. Όμως η έννοια της πρόβλεψης λόγω αντίληψης και συμπλήρωσης μοτίβου στον Τρίτο Νόμο είναι πιο γενική. Ας θεωρήσουμε τις παρακάτω προτάσεις:
Τελειώνει η βενζίνη, είναι σχεδόν
άδειο το ...
Η θερμοκρασία αύριο θα πέσει στους 12 ...
Αν πάμε έτσι, θα υποβιβαστούμε στη ...
Η λέξη που ακολουθεί στη θέση των τριών τελειών δεν μπορεί να είναι οποιαδήποτε· μάλλον μπορεί να προβλεφτεί αρκετά καλά. Π.χ. στο πρώτο παράδειγμα πρόκειται μάλλον για τη λέξη “ντεπόζιτο”, στο δεύτερο για τη λέξη “βαθμούς”, και στο τρίτο εξαρτάται από το θέμα: αν πρόκειται για συγκεκριμένο άθλημα, μπορεί π.χ. η λέξη να είναι “δεύτερη”, “τρίτη”, “βήτα”, κλπ, ακολουθούμενη από “εθνική”, “κατηγορία”, κλπ — πάντως αυτοί που συζητούν ξέρουν ακριβώς πώς λέγεται αυτό που ακολουθεί. Ακόμα και όταν η συγκεκριμένη λέξη δεν είναι δυνατό να προβλεφτεί, πιο συχνά προβλέπεται η γραμματική κατηγορία της λέξης. Π.χ., μετά από άρθρο αναμένουμε ουσιαστικό ή επίθετο με μεγαλη πιθανότητα, ενώ ένα ρήμα είναι πολύ απίθανο· αντίθετα, μετά από προσωπική αντωνυμία («εγώ ...») αναμένουμε μάλλον ρήμα, παρά ουσιαστικό. Όλα αυτά τα παραδείγματα μας δείχνουν οτι ο λόγος δεν είναι κάτι το εντελώς απρόβλεπτο. Όταν διαθέτουμε ήδη αρκετή εμπειρία από τα μοτίβα μιας γλώσσας που επαναλαμβάνονται κατά διάφορους τρόπους, μπορούμε να προβλέψουμε μέχρις ενός βαθμού αυτό που πρόκειται ν’ ακούσουμε. Μάλιστα, όταν το μοτίβο είναι κάθε φορά πανομοιότυπο, χωρίς καμία ποικιλία, όπως συμβαίνει σε φράσεις-κλισέ,
Είπε ο γάιδαρος τον πετεινό ...
τότε η πρόβλεψη είναι απόλυτα ακριβής. Αυτό μας δίνει μια ιδέα και για το τί συμβαίνει με τη μουσική. Σε μια μουσική μελωδία (που είναι γνωστή στον ακροατή), η επόμενη νότα είναι απόλυτα προβλέψιμη· αν ακούσουμε άλλη νότα από αυτήν που αναμένουμε, η εκτέλεση θα μας φανεί “παράφωνη”. Τα μουσικά μοτίβα όμως μπορεί να είναι και πιο αφηρημένα. Στη δυτική μουσική, λόγου χάρη, κάνουμε αποδεκτά ορισμένα μοτίβα, ώστε ακόμα και σ’ ένα κομμάτι που ακούμε για πρώτη φορά, αν η νότα που ακολουθεί είναι εκτός των όσων προβλέπονται από τα οικεία-μας δυτικά μοτίβα, αισθανόμαστε πως “κάτι δεν πάει καλά” στο συγκεκριμένο μουσικό κομμάτι. Άρα η πρόβλεψη βάσει μοτίβων παίζει σπουδαιότατο ρόλο και στον τομέα της μουσικής αντίληψης.
Ας προχωρήσουμε τώρα σε μία επιπλέον γενίκευση.
Όλα τα παραπάνω παραδείγματα αφορούσαν σε ακολουθιακές δομές. Δηλαδή, βάσει μιας σειράς (ακολουθίας) παραδειγμάτων, μας δίνεται η δυνατότητα να προβλέψουμε το επόμενο παράδειγμα. Αλλά η πρόβλεψη δεν είναι απαραίτητο να είναι ακολουθιακής φύσης. Μπορεί να αφορά σε περισσότερες από μία διαστάσεις. Ας θεωρήσουμε π.χ. την παρακάτω ελλιπή εικόνα:

Πρακτικά οποιοσδήποτε, ακόμα κι αν δεν έχει ανοίξει ποτέ-του βιβλίο φυσικής ή άλλο επιστημονικό, θα αναγνωρίσει από αυτό το 1/4 εικόνας τη φυσιογνωμία του Άλμπερτ Αϊνστάιν. Επομένως η “πρόβλεψη” δεν είναι μόνο ακολουθιακής φύσης, δηλαδή μονοδιάστατη, ούτε είναι απαραίτητο να συμπεριλαμβάνει τη διάσταση του χρόνου. Μπορεί αυτό που προβλέπουμε να είναι δύο ή τριών διαστάσεων και να πρόκειται για κάτι το στατικό στο χώρο. Ακόμα κι αν δεν αναγνωρίζαμε τον Αϊνστάιν στο παραπάνω τμήμα φωτογραφίας, σίγουρα μπορούμε ν’ αναγνωρίσουμε οτι πρόκειται για πρόσωπο ηλικιωμένου ανθρώπου. Αυτό μας δίνει μια ιδέα για το από πού μπορεί να προέρχεται ο Τρίτος Νόμος, δηλαδή ποια είναι η βιολογική-του βάση. Ας ρίξουμε μια ματιά στην ακόλουθη εικόνα:

Έστω οτι τόσο μόνο — όσο δείχνει η εικόνα — περιλαμβάνεται στο οπτικό-μας πεδίο, δηλαδή δεν μπορούμε να δούμε πιο αριστερά. Όποιος οργανισμός που έχει καλή όραση (όχι μόνο άνθρωπος, αλλά και ζώο) δεν μπορεί να προβλέψει οτι η ουρά και τα πίσω πόδια συμπληρώνονται από ένα ολόκληρο — και ίσως επικίνδυνο — ζώο (έναν γατόπαρδο στην προκείμενη περίπτωση), μάλλον δεν έχει και πολλές ελπίδες ν’ αφήσει απογόνους. Το ίδιο ισχύει και αν η συμπλήρωση της ελλιπούς εικόνας αντιστοιχεί σε κάποιο είδος τροφής. Σε ζώα με ικανότητα όρασης, η φυσική επιλογή ασφαλώς προέκρινε εκείνα που μπορούσαν να “προβλέψουν” (έστω και στοιχειωδώς, φτάνοντας στο γενικό ερέθισμα “κίνδυνος!” ή “τροφή!”) το περιβάλλον-τους. Επομένως η ικανότητα συμπλήρωσης (“πρόβλεψης”) ενός ελλιπούς οπτικού μοτίβου πρέπει να είναι πολύ αρχαία. Αλλά και την ικανότητα ακολουθιακής πρόβλεψης στη διάσταση του χρόνου δεν την έχει μόνο ο άνθρωπος, αλλά και κάποια ζώα, όπως δείχνουν πειράματα με αρουραίους. (Π.χ. οι αρουραίοι μπορούν να προβλέψουν, αν έχουν εκπαιδευτεί κατάλληλα, οτι στο τέταρτο χτύπημα ενός κουδουνιού θ’ ανοίξει το καπάκι με την τροφή, όπως θα δούμε στον Πέμπτο Νόμο.)
Στον άνθρωπο πάντως, αυτή η ικανότητα αντίληψης μοτίβων έγινε μια από τις πιο ουσιαστικές ικανότητες επιβίωσης, πράγμα που εντυπώθηκε στον ανθρώπινο νου υποσυνείδητα, και τον οδήγησε και οδηγεί πολλές φορές σε λάθος συμπεράσματα: ο άνθρωπος προσπαθεί πολύ συχνά ν’ ανακαλύψει μοτίβα εκεί που δεν υπάρχουν. Έβλεπε το πέταγμα των πουλιών (στην ελληνική αρχαιότητα για παράδειγμα), και απ’ αυτό προσπαθούσε να μαντέψει το μέλλον· το ίδιο προσπαθούσε — και δυστυχώς προσπαθεί ακόμα και σήμερα — να κάνει παρατηρώντας τη θέση των πλανητών στον ουράνιο θόλο (αστρολογία), τις ρυτιδώσεις σε μια παλάμη (χειρομαντεία), ή το είδος των χαρτιών που διαλέγονται από μια τράπουλα (χαρτομαντεία). Όλες αυτές οι προλήψεις, και πολλές άλλες, προέρχονται από την “αγωνία” του ανθρώπου να προβλέψει το μέλλον, χωρίς να καταλαβαίνει οτι δεν υπάρχει μοτίβο, δηλαδή δεν υπάρχει σχέση αίτιου–αιτιατού μεταξύ αυτών που παρατηρεί και αυτών που προσπαθεί να προβλέψει. (Π.χ., δεν υπάρχει τέτοια σχέση μεταξύ της θέσης των πλανητών και του τί συμβαίνει στην επιφάνεια της Γης, εκτός από γνωστά αστρονομικά φαινόμενα, όπως οι παλίρροιες.) Αυτό το “ανθρώπινο λάθος” δεν εξαλείφθηκε μέσω φυσικής επιλογής, γιατί δεν είναι καταστροφικό αν επιχειρήσει κανείς να κάνει μια λάθος πρόβλεψη· καταστροφικό είναι το να μη μπορεί (και άρα να μην επιχειρήσει) να κάνει πρόβλεψη.
Το πώς υλοποιείται αυτή η ικανότητα για πρόβλεψη μέσω της αντίληψης μοτίβων στον Τρίτο Νόμο είναι ένα ανοιχτό ερώτημα. Είναι γνωστή η απάντηση σε επίπεδο νευρώνων και αντίληψης εικόνας, αλλά δεν είναι γνωστή η λύση του προβληματος στην πλήρη γενικότητά του, ώστε να αντιμετωπίζονται όλα τα παραδείγματα που αναφέρθηκαν παραπάνω. Το πώς παριστάνεται στο νου γενικά ένα μοτίβο οποιασδήποτε μορφής — αυτό είναι το κατεξοχήν αναπάντητο ερώτημα.
Τέταρτος Νόμος: Ελαχιστοποίηση Δομής (“Ξυράφι του Όκαμ”)
Όπως και στους προηγούμενους τρεις Νόμους, έτσι και στον Τέταρτο, θα ξεκινήσουμε από το γενικό, αφηρημένο, και απαντώμενο στην ανθρώπινη νόηση μόνο, και στη συνέχεια θα δούμε την “ταπεινή” βιολογική προέλευση του νόμου αυτού.
Στη φιλοσοφία, αλλά και στην επιστήμη, υπάρχει ένας “μετα-κανόνας” που είναι γνωστός σαν “ξυράφι του Όκαμ” (αγγλ.: “Ockham’s razor”). Ονομάζεται έτσι λόγω του Άγγλου φιλοσόφου του Μεσαίωνα William of Ockham (ή Occam· Γουΐλλιαμ οβ Όκαμ, ~1285 – ~1349), που πρώτος τον διατύπωσε, και λέει το εξής:
| Ξυράφι του
Όκαμ: Δεν πρέπει να γίνεται εισαγωγή υποθέσεων χωρίς λόγο. |
Μια ισοδύναμη έκφραση του ίδιου κανόνα είναι οτι μεταξύ δύο θεωριών που βασίζονται σε δύο διαφορετικά σύνολα υποθέσεων, προτιμητέα είναι η θεωρία εκείνη που έχει το απλούστερο (πιο λιτό) σύνολο υποθέσεων.
Παράδειγμα: το Μεσαίωνα κάποιοι θεολόγοι πίστευαν οτι οι πλανήτες κινούνται στις τροχιές-τους επειδή τους σπρώχνουν άγγελοι. Επιφανειακά αυτό φαίνεται σαν μια απλή εξήγηση. Όταν όμως την εξετάσουμε λίγο πιο προσεκτικά, θα δούμε οτι εγείρει πιο πολλά ερωτήματα απ’ όσα προσπαθεί να απαντήσει. Π.χ., πόσοι είναι αυτοί οι άγγελοι; Ο αριθμός-τους εξαρτάται από το μέγεθος του πλανήτη (ή τη λαμπρότητα, εφόσον το μέγεθος ήταν άγνωστο το Μεσαίωνα), ή όχι; Γιατί σπρώχνουν μερικούς πλανήτες αργά και άλλους πιο γρήγορα; Κάνουν και κάποια άλλη δουλειά οι άγγελοι αυτοί ή είναι εντεταλμένοι να κάνουν μόνο τη συγκεκριμένη από καταβολής κόσμου; Στη δεύτερη περίπτωση, σε τί διαφέρουν οι άγγελοι αυτοί από ένα μηχανισμό όπως την έλικα ενός πλοίου; κ.ο.κ. Μπορεί κανείς να δημιουργήσει ένα πλήθος αναπάντητα ερωτήματα, για καθένα από τα οποία πρέπει να δοθεί απάντηση που θα βασίζεται σε μια αυθαίρετη υπόθεση. (Π.χ.: «Ναι, ο αριθμός των αγγέλων είναι ανάλογος της λαμπρότητας του πλανήτη», ή: «Όχι, ο αριθμός-τους είναι σταθερός και ίσος με 74.») Η “θεωρία” λοιπόν περί αγγέλων για την κίνηση των πλανητών χρειάζεται ένα μεγάλο πλήθος υποθέσεων. Αντίθετα, η μετέπειτα θεωρία της βαρύτητας, που διατυπώθηκε από το Νεύτωνα, βασίζεται σε ένα πολύ μικρότερο πλήθος υποθέσεων, και επιπλέον εξηγεί και ένα μεγαλύτερο αριθμό φαινομένων, όπως το γιατί όλα τα αντικείμενα πέφτουν προς το κέντρο της Γης, γιατί δημιουργούνται οι παλίρροιες, κλπ. Η κλασική θεωρία της βαρύτητας είναι ένα πιο “λιτό” επεξηγηματικό σύστημα, οπότε η θεωρία περί αγγέλων κόβεται από το ξυράφι του Όκαμ και απορρίπτεται.
Το ξυράφι του Όκαμ είναι ένας “μετα-κανόνας” επειδή μας λέει ποιο σύστημα κανόνων να προτιμήσουμε όταν έχουμε περισσότερα από ένα. (Θα μπορούσαμε να το πούμε και “κανόνα δεύτερου βαθμού”.) Η εγκυρότητά του οφείλεται στο οτι σχεδόν πάντα, όταν βρισκόμαστε αντιμέτωποι με δύο ή περισσότερα επεξηγηματικά συστήματα στη φύση, το σύστημα που ισχύει στην πραγματικότητα (δηλαδή εκείνο με το οποίο συμφωνεί η παρατήρηση και το πείραμα) είναι εκείνο που έχει τις λιγότερες υποθέσεις.
Επίσης, πέρα από τα φυσικά συστήματα, και στα μαθηματικά όταν υπάρχουν δύο αποδείξεις του ίδιου θεωρήματος, οι μαθηματικοί προτιμούν πάντα την πιο λιτή· και μεταξύ δύο αξιωματικών συστημάτων, προτιμούν πάντα αυτό με τα λιγότερα αξιώματα.(*)
Παρόλο που τόσο οι φιλόσοφοι όσο και οι επιστήμονες είναι άριστα εξοικειωμένοι με το ξυράφι του Όκαμ, εντούτοις οι πιο πολλοί απ’ αυτούς το δέχονται σαν έναν κανόνα που “απλώς ισχύει”, χωρίς ν’ αντιλαμβάνονται το γιατί ισχύει, δηλαδή την προέλευσή του. Το ξυράφι του Όκαμ έχει κι αυτό τις ρίζες-του στην ανθρώπινη νόηση, και μάλιστα — και πάλι — στην αίσθηση της όρασης. Ας θεωρήσουμε το παρακάτω απλούστατο σχήμα:

Πώς θα μπορούσαμε να περιγράψουμε αυτό που βλέπουμε παραπάνω; Έστω οτι δεν έχουμε ιδέα περί αλφαβήτων (π.χ. είμαστε στην προ αλφαβήτων εποχή, ή σε περιοχές του κόσμου όπου το ελληνικό αλφάβητο και τα παράγωγά του δεν είχαν διαδοθεί ακόμα), οπότε δεν μπορούμε να πούμε οτι αυτό είναι «το γράμμα χι», ή «το λατινικό X». Επίσης δεν έχουμε ιδέα περί μαθηματικών συμβόλων, άρα ούτε το «σύμβολο του πολλαπλασιασμού» είναι δεκτό σαν απάντηση. Και πάλι όμως υπάρχει τρόπος να περιγράψουμε αυτό που βλέπουμε. Μπορούμε π.χ. να πούμε οτι είναι δυο ισομεγέθη ξυλάκια, πλαγιασμένα προς την αντίθετη πλευρά το ένα από το άλλο, και βαλμένα το ένα πάνω στο άλλο, έτσι ώστε να συμπίπτουν στο μέσον-τους. Με άλλα λόγια, βλέπουμε το σχήμα αυτό έτσι:

Θα μπορούσαμε μάλιστα να κάνουμε και ένα πείραμα στο εργαστήριο για να διαπιστώσουμε οτι όντως έτσι “βλέπουν” το σχήμα αυτό οι περισσότεροι άνθρωποι, όταν τους ζητηθεί να το περιγράψουν χωρίς να κάνουν χρήση αλφαβητικών ή μαθηματικών συμβόλων.
Αλλά ο παραπάνω τρόπος περιγραφής ενός Χ δεν είναι ο μοναδικός· υπάρχουν πάμπολλοι άλλοι τρόποι. Το παρακάτω διάγραμμα δείχνει τρεις άλλους τρόπους:
Γιατί όμως σχεδόν ποτέ δεν βλέπουμε ένα Χ σαν αποτελούμενο από τα παραπάνω μέρη;
Ο λόγος είναι οτι εφαρμόζουμε ένα είδος “ξυραφιού του Όκαμ”, αλλά σε άμεση (δηλ. ταχύτατη), υποσυνείδητη, και “οπτική” μορφή. Αυτό που κάνουμε είναι οτι ελαχιστοποιούμε την περιγραφή της δομής του Χ (ή οποιουδήποτε σχήματος), επιλέγοντας την πιο λιτή δομή απ’ όλες τις δυνατές. Για να δούμε το γιατί το X = \ + / είναι η πιο λιτή περιγραφή, ας την αποτυπώσουμε με λόγια:
Το X αποτελείται από δύο ευθύγραμμα τμήματα ίσου μήκους, όπου το πρώτο έχει κλίση 45°, το δεύτερο –45° (ή 135°) (δηλ. / + \), και τα μέσα-τους συμπίπτουν (δηλ. X).
Κάθε άλλη περιγραφή είναι σαφώς μεγαλύτερη. Ας δούμε την πρώτη από τις παραπάνω “αφύσικες” περιγραφές, την X = V + Λ:
Το X αποτελείται από δύο τμήματα, το πρώτο από τα οποία είναι φτιαγμένο από δύο ισομήκη ευθύγραμμα τμήματα με κλίση –45° και 45° (δηλ. \ + /), που ενώνονται στο κατώτερό τους σημείο (δηλ. V)· ας ονομάσουμε το σημείο αυτό “μύτη”· το δεύτερο τμήμα είναι συμμετρικό με το πρώτο ως προς έναν οριζόντιο άξονα (δηλ. Λ), και τα δύο τμήματα είναι ενωμένα στις μύτες-τους (δηλ. X).
Αυτή η περιγραφή είναι σαφώς μεγαλύτερη από την πρώτη, και δεν φαίνεται να μπορεί να διατυπωθεί σημαντικά πιο σύντομα. Το ίδιο θα διαπιστώσουμε και για οποιαδήποτε άλλη περιγραφή, όπως αλλιώς και να “δουμε” το δοσμένο σχήμα X.
Απ’ όλες τις δυνατές περιγραφές λοιπόν, επιλέγουμε την πιο λιτή, τη συντομότερη. Αυτό το κάνουμε αυθόρμητα (υποσυνείδητα), χωρίς να μας έχει διδάξει κανένας πώς να το κάνουμε, ή γιατί να το κάνουμε. Απλά, έτσι δουλεύει η όρασή μας. Αν δεν δούλευε έτσι, θα είχαμε μια πολύπλοκη, εξαιρετικά μπερδεμένη εικόνα για το πώς δομούνται τα διάφορα αντικείμενα στον κόσμο.
Φυσικά, η ικανότητα ελαχιστοποίησης της δομής αντικειμένων δεν περιορίζεται σε τεχνητά αντικείμενα όπως ένα X. Μπορεί π.χ. να πρόκειται για την ακόλουθη εικόνα:

Χωρίς το ξυράφι του Όκαμ (αλλά στην “οπτική”, όχι στη φιλοσοφική-του έκδοση) θα μπορούσαμε να δημιουργήσουμε διάφορες “θεωρίες” για το τί δείχνει η παραπάνω εικόνα, που ελάχιστη σχέση θα είχαν με την πραγματικότητα. Π.χ. μια τέτοια “θεωρία” θα μπορούσε να είναι οτι βλέπουμε δύο γατόπαρδους: το κεφάλι και τα μπροστινά άκρα του ενός, και τα ισχύα, πίσω άκρα, και ουρά ενός δεύτερου, ενώ στο μέσον-τους (μεταξύ των δύο δέντρων) είναι απλωμένη μόνο η γούνα ενός τρίτου γατόπαρδου, σαν ένα είδος πετσέτας, τοποθετημένη ώστε να “ταιριάζει” στη σειρά με τα δύο ζωντανά ζώα. Μπορεί επίσης αυτό που μοιάζει με τοίχο μεταξύ των δύο δέντρων να είναι κι αυτό κάτι σαν ταπετσαρία, ώστε να κρύβει τους δύο ζωντανούς γατόπαρδους. Πλήθος τέτοιων “θεωριών” μπορούν να διατυπωθούν, που περιορίζονται μόνο από τη φαντασία όποιου τις σκαρφίζεται. Όλες όμως εισάγουν υποθέσεις που είναι περισσότερες από την απλούστερη ερμηνεία της φωτογραφίας, οτι δηλαδή υπάρχει ένας και μοναδικός γατόπαρδος. Επίσης όλες έχουν το μεγάλο πρόβλημα οτι δεν αντιστοιχούν στην πραγματικότητα, η οποία μπορεί να είναι αμείλικτη σε καταστάσεις όπως η σωστή ερμηνεία μιας εικόνας που περιλαμβάνει όντα ίσως επικίνδυνα γι’ αυτόν που τη βλέπει, ή όντα χρήσιμα για τη συντήρησή του. Η πραγματικότητα επομένως, μέσω φυσικής επιλογής, δημιούργησε ζώα που αντιλαμβάνονται οπτικά τον κόσμο με τον πιο απέριττο, λιτό τρόπο, που είναι σχεδόν πάντα αυτός που δίνει τη “σωστή ερμηνεία”. Στην περίπτωση της ανθρώπινης νοημοσύνης, περάσαμε από το επίπεδο των απλών οπτικών σημάτων σ’ αυτό των αφηρημένων και γενικευμένων εννοιών, όπως μια μαθηματική αξιωματική θεωρία, ή μια φιλοσοφική ερμηνεία κάποιων καταστάσεων. Καθώς οι πρόγονοί μας από τη φύση-τους ήσαν φτιαγμένοι έτσι ώστε να εφαρμόζουν το ξυράφι του Όκαμ στο επίπεδο της εικόνας, το ίδιο συνεχίσανε να κάνουν και όταν πέρασαν σταδιακά στο επίπεδο της αφηρημένης έννοιας. Ακόμα και η παρούσα ενότητα περί Τέταρτου Νόμου, που δίνει μια και μοναδική εξήγηση σε φαινόμενα που μοιάζουν τόσο διαφορετικά, όπως η ερμηνεία εικόνας και οι φιλοσοφικές ή επιστημονικές θεωρίες, δεν αποτελεί παρά μια επιπλέον εφαρμογή του ίδιου νόμου.
Πριν ν’ αφήσουμε τη συζήτηση περί ξυραφιού του Όκαμ, ας δούμε μέσω αυτού και την εξήγηση ενός από τα οπτικά φαινόμενα (γνωστών και ως “οπτικές απάτες”) που παρουσιάζονται συχνά στα βιβλία ψυχολογίας:
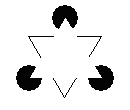
Το παραπάνω διάγραμμα δείχνει αυτό που είναι γνωστό σαν “αυταπάτη του Kanizsa”. Αυτό που πιστεύουμε οτι βλέπουμε είναι το εξής:
Τρεις μαύροι κύκλοι τοποθετημένοι στις κορυφές ενός ισόπλευρου τριγώνου, που επικαλύπτονται μερικώς από αυτό το “αόρατο” τρίγωνο, που επίσης επικαλύπτει ένα άλλο ανεστραμμένο τρίγωνο, του οποίου βλέπουμε μόνο το περίγραμμα.
Αυτό όμως που μόλις αναφέρθηκε δεν είναι παρά η λιτή περιγραφή, αυτή που προκύπτει λόγω του ξυραφιού του Όκαμ. Θα μπορούσε κανείς να ισχυριστεί οτι αυτό που δείχνει το διάγραμμα είναι το εξής:
Τρεις μαύρες φιγούρες σε σχήμα “πάκμαν”, τοποθετημένες στις κορυφές ενός ισόπλευρου τριγώνου, όπου το αριστερό “πάκμαν” έχει το ανοιχτό “στόμα” σε διεύθυνση 45°, το δεξιό σε διεύθυνση –45°, και το άνω σε διεύθυνση προς τα κάτω. Επίσης υπάρχουν τρεις γωνίες, 45° η καθεμία, αποτελούμενες από ισομήκη ευθύγραμμα τμήματα, στραμμένες προς διευθύνσεις... (κλπ.), και τοποθετημένες έτσι ώστε... (κλπ.).
Η παραπάνω περιγραφή δεν μας έρχεται αυθόρμητα στο νου γιατί είναι πολύ μεγαλύτερη. Αντ’ αυτής, το ξυράφι του Όκαμ προκρίνει την πρώτη περιγραφή, παρόλο που εκείνη βασίζεται στην ύπαρξη ενός “αόρατου τριγώνου”, που θα μπορούσε κανείς να ισχυριστεί οτι «δεν υπάρχει στην πραγματικότητα» (αφού καμιά ακμή-του δεν είναι πλήρως σχηματισμένη). Και όμως, όταν κοιτάμε το σχήμα νομίζουμε οτι “βλέπουμε” αυτό το αόρατο τρίγωνο, που είναι και ο λόγος που το παραπάνω ονομάζεται “αυταπάτη” (του Ιταλού ψυχολόγου Gaetano Kanizsa, που τη δημιούργησε το 1955).
Πέμπτος Νόμος: Αντίληψη Ποσότητας
Ας υποθέσουμε οτι βλέπουμε σε ένα χάρτη τα δύο παρακάτω νησιά:
Ποιο νησί είναι το μεγαλύτερο από τα δύο; Έστω οτι δεν αναγνωρίζουμε τα δυο αυτά νησιά, ή δεν έχουμε τη σχετική γεωγραφική γνώση ώστε να δώσουμε αμέσως μια απάντηση από μνήμης.(*) Και πάλι όμως, μπορούμε ν’ αντιληφθούμε “με το μάτι” οτι το νησί στα δεξιά είναι ελαφρώς μεγαλύτερο από εκείνο στ’ αριστερά. Αλλά με ποιον τρόπο καταφέρνει “το μάτι” ένα τέτοιο κατόρθωμα;
Ας σκεφτούμε τώρα ένα άλλο κατόρθωμα σύγκρισης, φαινομενικά διαφορετικής φύσης. Έστω οτι αναρωτιόμαστε το εξής: ποιο από τα δύο γράμματα, το μυ ή το ταυ είναι πιο συχνό στην ελληνική γλώσσα;
Χωρίς να μετρήσουμε τη συχνότητα των γραμμάτων από κάποιο παράδειγμα κειμένου, έχουμε την “αίσθηση” οτι το ταυ πρέπει να είναι πιο συχνό από το μυ. Κι αν θελήσουμε να συγκρίνουμε το μυ με το βήτα (στο γραπτό λόγο, όχι σαν φθόγγους), πάλι είμαστε αρκετά σίγουροι οτι το μυ πρέπει να είναι πιο συχνό.
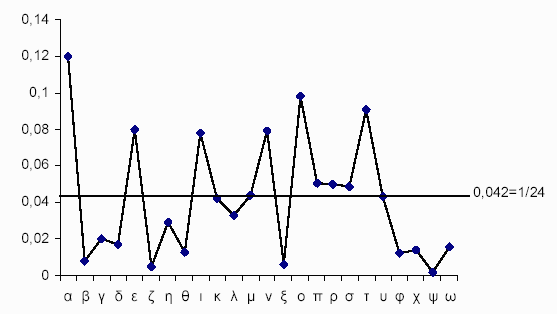
Πράγματι, μια ματιά σε δεδομένα από μετρήσεις (βλ. διάγραμμα) μας πείθει οτι το ταυ είναι το πιο συχνό σύμφωνο, το μυ βρίσκεται περίπου στο μέσον των συχνοτήτων, και το βήτα είναι από τα πιο σπάνια γράμματα. Πώς τα “ξέρουμε” όλα αυτά χωρίς να μας πει κανείς ποτέ οτιδήποτε για τη συχνότητα των γραμμάτων;
Τέλος, ας ρίξουμε μια ματιά (στην κυριολεξία όμως “μια ματιά” — θα δούμε αμέσως γιατί) στις παρακάτω εικόνες που δείχνουν κόσμο συγκεντρωμένο. Έστω οτι μας ζητείται να τις ταξινομήσουμε κατ’ αύξον μέγεθος πλήθους (δηλ. η φωτογραφία με τα λιγότερα άτομα να δειχτεί σαν πρώτη, εκείνη με τα αμέσως περισσότερα άτομα δεύτερη, κ.ο.κ.) χωρίς όμως να μετρήσουμε ένα-ένα τα άτομα των φωτογραφιών:
 |
 |
 |
 |
|||
| (α) | (β) | (γ) | (δ) |
Πράγματι, χωρίς να μπούμε στον κόπο να μετρήσουμε οτιδήποτε, κυριολεκτικά “ρίχνοντας μια ματιά”, μπορούμε να πούμε αμέσως οτι τα λιγότερα άτομα έχει η φωτογραφία (γ), ακολουθεί η (α), μετά είναι η (δ), και τα πιο πολλά άτομα έχει η (β). Πώς μπορούμε να το κάνουμε αυτό χωρίς να μετρήσουμε; Σίγουρα δεν είναι το μέγεθος του καθενός ατόμου ή προσώπου που χησιμοποιούμε σαν οδηγό, γιατί τα πρόσωπα στη φωτογραφία (γ) (που έρχεται πρώτη στην ταξινομημένη λίστα) δεν είναι ούτε τα μεγαλύτερα, ούτε τα μικρότερα σε μέγεθος. Ούτε μπορεί να είναι οι αποστάσεις μεταξύ των ατόμων που μας δίνουν (υποσυνείδητα) τη λύση, γιατί στις φωτογραφίες (α), (γ), και (δ), οι αποστάσεις είναι λίγο-πολύ ίσες, άρα ούτε αυτό το στοιχείο μας βοηθά στην ταξινόμηση. Κάτι άλλο συμβαίνει. Όπως θα δούμε, η νόηση χρησιμοποιεί τον ίδιο μηχανισμό για να λύσει καί τα τρία παραπάνω προβλήματα, όπως και άλλα παρόμοια.
Το τρίτο παράδειγμα (αυτό με το πλήθος των ανθρώπων) έρχεται πιο κοντά στον πυρήνα του νοητικού μηχανισμού, γιαυτό είναι χρήσιμο να το εξετάσουμε πιο διεξοδικά. Έχουν γίνει πειράματα στο εργαστήριο όπου παρουσιάζονται στα υποκείμενα διαγράμματα όπως το παρακάτω:

Τα διαγράμματα αυτά, που περιέχουν διαφορετικούς αριθμούς κουκκίδων αριστερά και δεξιά κάθε φορά, εμφανίζονται σε οθόνη υπολογιστή μόνο για μερικά χιλιοστά του δευτερολέπτου (π.χ., 25 ms), και αμέσως αντικαθίστανται από μια ουδέτερη οθόνη, όπως περίπου φαίνεται στο επόμενο διάγραμμα (με τη διαφορά οτι το πότε εμφανίζεται η επόμενη οθόνη είναι υπό τον πλήρη έλεγχο του υποκειμένου).

Από τα υποκείμενα ζητείται να προσηλώσουν το βλέμμα-τους στο κεντρικό σημείο (το σταυρουδάκι), και μόλις δουν το καρέ με τις κουκκίδες, να πατήσουν όσο πιο γρήγορα μπορούν ένα κουμπί στ’ αριστερά του πληκτρολογίου (π.χ. το Q) αν πιστεύουν οτι η αριστερή ομάδα έχει περισσότερες κουκκίδες, ή ένα κουμπί στα δεξιά (π.χ. το P) αν πιστεύουν οτι περισσότερες κουκκίδες έχει η δεξιά ομάδα. Μόλις δώσουν την απάντησή τους, πατάνε π.χ. το [κενό] προκειμένου να εμφανιστεί το επόμενο καρέ με τις κουκκίδες (οπότε τον έλεγχο του πότε εμφανίζεται η επόμενη οθόνη τον έχει το υποκείμενο).
Από τα πειράματα αυτά (που έχουν γίνει όχι μόνο με κουκκίδες, αλλά και με διάφορα άλλα αντικείμενα, όπως γραμμές, γεωμετρικά σχήματα, ψηφία, κλπ.) έχουν βγει τα εξής αναμφισβήτητα (και λίγο-πολύ αναμενόμενα) συμπεράσματα:
-
Όσο πιο μεγάλη η διαφορά των αριθμών, τόσο πιο σωστά απαντάνε τα υποκείμενα· είναι ευκολότερο να διακρίνει κανείς τη διαφορά μεταξύ 7 και 20 κουκκίδων, παρά μεταξύ 7 και 8.
-
Όσο πιο μικροί είναι οι συγκρινόμενοι αριθμοί, τόσο πιο σωστά απαντάνε τα υποκείμενα· είναι ευκολότερο να διακρίνει κανείς τη διαφορά μεταξύ 7 και 8 κουκκίδων, παρά μεταξύ 17 και 18.
-
Το πόσο γρήγορα απαντάνε τα υποκείμενα εξαρτάται από το πόσο παρόμοιοι είναι οι συγκρινόμενοι αριθμοί: όσο πιο κοντινοί οι αριθμοί, τόσο περισσότερη ώρα (κατά μέσο όρο) κάνουν να αποφασίσουν τα υποκείμενα.
Πώς μπορούμε να εξηγήσουμε τις παραπάνω τρεις πειραματικές παρατηρήσεις;
Το μοντέλο συσσωρευτή
Οι παρατηρήσεις αυτές εξηγούνται ως έναν ικανοποιητικό βαθμό από το λεγόμενο “μοντέλο συσσωρευτή”. Το μοντέλο συσσωρευτή είναι μια προσπάθεια να περιγραφεί το τί συμβαίνει στον εγκέφαλο του ανθρώπου (αλλά και πολλών άλλων ζώων, όπως θα δούμε) όταν αντιλαμβανόμαστε ποσότητες. Σύμφωνα με το μοντέλο αυτό, συμβαίνει το εξής:
Έστω οτι η εμφάνιση της κάθε “κουκκίδας” (ή γενικότερα του κάθε αντικειμένου, αφού όπως είδαμε στο παράδειγμα με τις φωτογραφίες ανθρώπων μπορεί αυτό του οποίου αντιλαμβανόμαστε την ποσότητα να είναι κάτι το πολύπλοκο) προκαλεί την έκκριση μιας ποσότητας κάποιας ουσίας στον εγκέφαλο. Η ποσότητα αυτή είναι “περίπου ίδια” για κάθε κουκκίδα, αλλά όχι ακριβώς ίδια. Δηλαδή, με τη μια κουκκίδα μπορεί να είναι 5,32 μg (μικρογραμμάρια), με την επόμενη κουκκίδα μπορεί να εκκριθούν 5,28 μg, κ.ο.κ., έτσι ώστε η μέση τιμή της εκκρινόμενης ποσότητας να είναι π.χ. 5,30 μg, αλλά βέβαια η πραγματική ποσότητα να “παίζει” τυχαία γύρω από αυτή τη μέση τιμή. Οι ποσότητες της ουσίας αυτής (που προκαλούνται από την αντίληψη της κάθε κουκκίδας) συσσωρεύονται σε ένα σημείο, ένα “συσσωρευτή” (εξ ου και το όνομα του μοντέλου). Έτσι, με 20 κουκκίδες, ο συσσωρευτής θα περιλαμβάνει 20 φορές την ποσότητα “περίπου 5,30” μg, που σημαίνει 20 Χ ~5,30 = ~106 μg. Όμως το “περίπου” των 106 μg των 20 κουκκίδων θα πρέπει να κυμαίνεται σ’ ένα μεγαλύτερο εύρος από το “περίπου” των 5,30 μg της μιας κουκκίδας, γιατί προσθέτοντας είκοσι “περίπου”, το σφάλμα μεγαλώνει. (Επαναλαμβάνουμε οτι η αριθμητική τιμή των 5,30 μg είναι εντελώς υποθετική· απλώς μας βοηθά στο να συγκεκριμενοποιήσουμε το παράδειγμα· αυτό που απαιτεί το μοντέλο του συσσωρευτή είναι κάποια τιμή.)
Αν η προστιθέμενη ποσότητα ήταν πάντα ακριβώς 5,30 μg, τότε οι 20 κουκκίδες θα προκαλούσαν την έκκριση ακριβώς 106 μg της ουσίας. Επειδή όμως η ποσότητα είναι περίπου 5,30, με 20 κουκκίδες παίρνουμε μια κατανομή συνολικής ποσότητας, με μέση τιμή 106, και με κάποια διασπορά γύρω από αυτή την τιμή, πράγμα που απεικονίζεται στο παρακάτω σχήμα:
Η καμπύλη του σχήματος (που λέγεται “κωδωνοειδής”, ή “γκαουσιανή”, ή “κανονική κατανομή”) μας λέει οτι τις πιο πολλές φορές οι 20 κουκκίδες προκαλούν την έκκριση συνολικής ποσότητας γύρω στα 106 μg (εκεί όπου η καμπύλη φτάνει στο μέγιστο ύψος). Άλλες φορές όμως (πιο σπάνια) οι 20 κουκκίδες μπορεί να παράγουν ποσότητα γύρω στα 105 μg (πιο λίγη), ή γύρω στα 107 μg (πιο πολλή). Σε ακόμα πιο σπάνιες περιπτώσεις, η ποσότητα μπορεί να είναι τόσο λίγη όσο 104 μg, ή τόσο πολλή όσο 108 μg, κλπ.
Όταν λοιπόν το δεδομένο είναι στην πραγματικότητα 20 κουκκίδες, ανταποκρινόμαστε σ’ αυτό με την έκκριση μιας ποσότητας της ουσίας, που είναι συνήθως γύρω στα 106 μg. Μπορεί όμως να τύχει να παραχθεί λιγότερη ή περισσότερη ποσότητα, οπότε έτσι θα αντιληφθούμε αντίστοιχα λιγότερες ή περισσότερες κουκκίδες. Η πιθανότητα βαίνει μειούμενη όσο απομακρυνόμαστε από τη σωστή τιμή για τις 20 κουκκίδες.
Πώς εξηγούνται οι τρεις πειραματικές παρατηρήσεις, που αναφέρθηκαν νωρίτερα, μέσω του μοντέλου του συσσωρευτή;
Η 1η παρατήρηση λέει οτι όσο πιο μεγάλη η διαφορά των αριθμών, τόσο πιο σωστά απαντάνε τα υποκείμενα. Έτσι, για παράδειγμα, είναι ευκολότερο να διακρίνει κανείς τη διαφορά μεταξύ 7 και 20 κουκκίδων, παρά μεταξύ 7 και 8. Το παρακάτω διάγραμμα δείχνει την κατανομή της ποσότητας της ουσίας για 7, 8, και 20 κουκκίδες:
Η κατανομή για 7 κουκκίδες σημειώνεται με κόκκινο χρώμα, εκείνη για 8 με πράσινο, και εκείνη για 20 με μπλε. Κατ’ αρχήν ας παρατηρήσουμε οτι όσο πιο μεγάλοι είναι οι αριθμοί, τόσο πιο “πλατιά” η κατανομή-τους. Αυτό είναι φυσικό, γιατί οι πιο μεγάλοι αριθμοί προέρχονται από πιο πολλές αθροίσεις από την “περίπου σταθερή” ποσότητα της ουσίας, άρα έχουν μεγαλύτερη πιθανότητα σφάλματος. Τώρα, για να γίνει σφάλμα μεταξύ 7 και 20 (δηλαδή για να μπερδέψουμε τις 7 κουκκίδες και να τις εκλάβουμε για 20, ή αντίστροφα), πρέπει η ουσία στον συσωρευτή να είναι τόση όση εκεί που σημειώνεται η περιοχή με μωβ χρώμα, επειδή εκεί συμπίπτουν οι κατανομές του 7 και του 20. Όπως βλέπουμε, αυτή η περιοχή είναι ελάχιστη (και το διάγραμμα τη μεγεθύνει, ενώ στην πραγματικότητα είναι ακόμα μικρότερη — εντελώς μηδαμινή). Οπότε αντίστοιχα ελάχιστη είναι και η πιθανότητα να μπερδέψουμε τις 7 κουκκίδες και να πούμε οτι είναι 20 (ή αντιστρόφως: να πούμε οτι οι 20 κουκκίδες είναι 7). Αντίθετα, η περιοχή όπου οι κατανομές του 7 και του 8 συμπίπτουν, που σημειώνεται με κίτρινο χρώμα, είναι αρκετά μεγάλη, οπότε αντίστοιχα μεγάλη είναι η πιθανότητα να εκλάβουμε τις 7 κουκκίδες για 8, ή τις 8 για 7.
Η 2η παρατήρηση λέει οτι όσο πιο μικροί είναι οι συγκρινόμενοι αριθμοί, τόσο πιο σωστά απαντάνε τα υποκείμενα· είναι ευκολότερο να διακρίνει κανείς τη διαφορά μεταξύ 7 και 8 κουκκίδων, παρά μεταξύ 17 και 18. Η εξήγηση δίνεται από το παρακάτω διάγραμμα:
Βλέπουμε λοιπόν οτι η περιοχή όπου αλληλοκαλύπτονται οι ποσότητες 7 και 8 (κίτρινη) είναι πολύ μικρότερη από την αντίστοιχη περιοχή όπου αλληλοκαλύπτονται οι ποσότητες 17 και 18 (επίσης κίτρινη). Άρα υπάρχει σημαντικά μεγαλύτερη πιθανότητα να κάνουμε λάθος εκτίμηση του αριθμού των κουκκίδων στην περίπτωση του δεύτερου ζεύγους, παρά στην περίπτωση του πρώτου.
Τέλος, η 3η παρατήρηση εξηγείται κι αυτή με παρόμοιο τρόπο: όσο πιο κοντινές είναι οι συγκρινόμενες ποσότητες, τόσο πιο μεγάλη είναι η αλληλοκάλυψή τους, επομένως ανάλογα τόσο πιο μεγάλο χρόνο παίρνει στο υποκείμενο να βεβαιωθεί νοητά για τη διαφορά των δύο ποσοτήτων.
Ας σημειωθεί οτι το μοντέλο συσσωρευτή δεν είναι υποχρεωτικά απόλυτα σωστό· έχουν παρατηρηθεί και κάποια αποτελέσματα που δεν συμφωνούν με το μοντέλο αυτό. Πάντως παραμένει μια πολύ καλή προσέγγιση των όσων παρατηρούμε στην πραγματικότητα.
Τώρα, πώς εξηγούνται μέσω του μοντέλου συσσωρευτή τα παραδείγματα που αναφέρθηκαν στην αρχή της ενότητας; Ας θυμηθούμε το παράδειγμα με τα δύο νησιά: πώς αντιλαμβανόμαστε οτι το νησί στα δεξιά είναι ελαφρώς μεγαλύτερο από εκείνο στα δεξιά;
Μια πιθανή απάντηση είναι οτι η οπτική “μηχανή” του εγκεφάλου-μας “διακριτοποιεί” αυτό που μας φαίνεται σαν συνεχής επιφάνεια του νησιού, δηλαδή την αναλύει σε πολλές μικρές διακριτές περιοχές (στο διάγραμμα οι περιοχές αυτές σημειώνονται με μια τελεία η κάθε μία). Έτσι, αυτό που γίνεται υποσυνείδητα είναι “σύγκριση ποσοτήτων” μέσω του μοντέλου συσσωρευτή. Με άλλα λόγια, υποσυνείδητα συγκρίνουμε “αριθμούς κουκκίδων”,(*) παρόλο που συνειδητά δεν το καταλαβαίνουμε οτι κάνουμε κάτι τέτοιο, γιατί το μόνο που αντιλαμβανόμαστε με το συνειδητό μέρος του νου είναι οι δύο συνεχείς επιφάνειες, οπότε μας φαίνεται οτι συγκρίνουμε εμβαδά επιφανειών.
Στο παράδειγμα της “αίσθησης” της συχνότητας γραμμάτων της ελληνικής γλώσσας, αυτό που αντιλαμβανόμαστε δεν είναι ο αριθμός των γραμμάτων όπως τα ταυ, μυ, και βήτα που έχουμε δει μέχρι τώρα (αφού ο συνολικός αριθμός-τους είναι μια τεράστια ποσότητα), αλλά η συχνότητά τους. Συγκρίνουμε δηλαδή τις συχνότητές τους σαν μεγέθη που μπορούν να “διακριτοποιηθούν”, με παρόμοιο τρόπο όπως κάνουμε και με τις επιφάνειες των νησιών στο προηγούμενο παράδειγμα.
Προέλευση του Πέμπτου Νόμου
Ασφαλώς δεν θα αποτελούσε έκπληξη αν μαθαίναμε οτι και η ικανότητά μας να αντιλαμβανόμαστε την ποσότητα με τον τρόπο που περιγράφηκε δεν μας ήρθε “ουρανοκατέβατη”, “από το πουθενά”, αλλά έχει τις ρίζες-της στη νόηση των ζώων. Πράγματι, έχουν γίνει πάμπολλα πειράματα και έχει δειχτεί οτι ζώα όπως ποντίκια, διάφορα πουλιά, γάτες, πίθηκοι, και άλλα πολλά, διαθέτουν στοιχειώδη ικανότητα αντίληψης μικρών αριθμών. Τα ζώα δεν μπορούν να μετράνε («ένα, δύο, ...») όπως εμείς, αλλά μπορούν να διακρίνουν π.χ. τα τρία αντικείμενα από τα τέσσερα, ή τα τέσσερα από τα πέντε, κλπ. Η ικανότητα αυτή εξαρτάται από το είδος του ζώου. Π.χ. το αμερικανικό ρακούν μπορεί να διακρίνει την ποσότητα μέχρι περίπου το πέντε ή έξι, ενώ από κει και πέρα μπερδεύεται και οι αποκρίσεις-του είναι μάλλον τυχαίες· αντίθετα, τα περιστέρια μπορούν να διακρίνουν τη διαφορά μεταξύ 45 και 50 χτυπημάτων με το ράμφος (ενώ και για μας τους ανθρώπους δεν είναι εύκολο να διακρίνουμε τη διαφορά μεταξύ 45 και 50 ήχων ενός κουδουνιού). Θα επαναλάβουμε στο σημείο αυτό οτι αναφερόμαστε αποκλειστικά στην αντίληψη ποσότητας, και όχι στο μέτρημα. Το μέτρημα είναι ανθρώπινη ικανότητα και μόνο, απαιτεί συντονισμό ανώτερων εγκεφαλικών λειτουργιών, μαθαίνεται μετά το τέταρτο ή πέμπτο έτος της ηλικίας του ανθρώπου, και είναι μάλλον άσχετο με τον Πέμπτο Νόμο. Αντίθετα, αντίληψη ποσότητας χωρίς μέτρημα έχουν και τα νεογέννητα μωρά, ως ένα βαθμό.
Θα περιγράψουμε εδώ πειράματα που έγιναν με αρουραίους το 2ο μισό του 20ού αιώνα. Σε ένα πείραμα που έγινε από τον Francis Mechner το 1958, και επαναλήφθηκε με παραλλαγές από τους John R. Platt και David M. Johnson το 1971, πεινασμένοι αρουραίοι εκπευδεύτηκαν και έμαθαν να χτυπούν έναν αριθμό φορών ένα μοχλό — ας τον πούμε μοχλό Α — πρωτού με ένα τελευταίο χτύπημα σε δεύτερο μοχλό — το μοχλό Β — να ανοίγουν το καπάκι που ελευθέρωνε την τροφή. Ο κάθε αρουραίος μάθαινε μέσω δοκιμής και λάθους οτι αρκούν π.χ. 4 χτυπήματα στο μοχλό Α και ένα τελευταίο στο μοχλό Β ώστε ν’ ανοίξει το καπάκι με το φαγητό.(*) (Ο κάθε αρουραίος εκπαιδευόταν σε συγκεκριμένο αριθμό.) Το πολύ “πρώιμο” πάτημα του μοχλού Β (χωρίς αρκετό αριθμό πατημάτων στον Α) είχε σαν αποτέλεσμα ένα μικρό ηλεκτροσόκ, γιατί χωρίς αυτή την “τιμωρία” το ζώο έτεινε να πατάει αμέσως το μοχλό Β, οπότε δεν μάθαινε τίποτα. Η έννοια της ποσότητας (αριθμού χτυπημάτων στο μοχλό Α) έτσι όπως την έμαθαν οι αρουραίοι απεικονίζεται στο παρακάτω διάγραμμα:
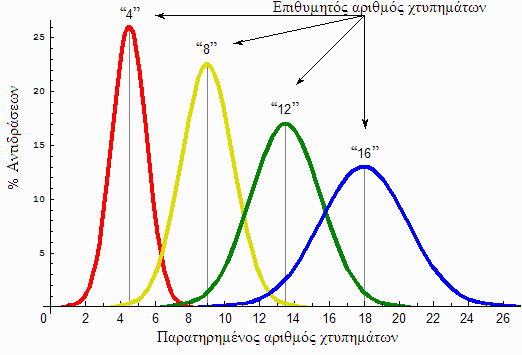
Ας δούμε τί σημαίνει π.χ. η μπλε καμπύλη: η μπλε καμπύλη δείχνει το πώς αντέδρασαν στον επιθυμητό αριθμό 16 χτυπημάτων τα ζώα αυτά: ενώ ο αριθμός που έπρεπε να μάθουν (δηλ. η ποσότητα που έπρεπε να εκτιμήσουν) ήταν το 16, οι αρουραίοι αντιδρούσαν χτυπώντας το μοχλό Α κατά μέσο όρο 18 φορές, όπως μας δείχνει στον οριζοντιο άξονα το σημείο στο οποίο η καμπύλη παίρνει τη μέγιστη τιμή-της. Βέβαια κάποιες φορές οι αρουραίοι που έπρεπε να εκτιμήσουν το 16 χτυπούσαν π.χ. 13 ή 21 φορές το μοχλό Α, γιαυτό και η καμπύλη έχει τη διασπορά που βλέπουμε (είναι πλατιά). Οι αρουραίοι που έπρεπε να εκτιμήσουν τον αριθμό 4 (κόκκινη καμπύλη), έδιναν κατά μέσο όσο 4,5 χτυπήματα, αλλά ήσαν πιο ακριβείς (η κόκκινη καμπύλη είναι πιο στενή). Γενικά, βλέπουμε οτι όσο μεγαλώνει ο αριθμός (η ποσότητα) που πρέπει να εκτιμηθεί, τόσο λιγότερο ακριβής γίνεται η εκτίμηση από το ζώο.
Τα αποτελέσματα αυτά συμφωνούν ως ένα μεγάλο βαθμό με το μοντέλο συσσωρευτή. Δηλαδή είναι σαν ο οργανισμός να έχει στο νου (είτε το ζωικό είτε τον ανθρώπινο) ένα συσσωρευτή, στον οποίο συσσωρεύεται ποσότητα ουσίας, μέσω της οποίας γίνεται η εκτίμηση της ποσότητας κάποιου αντικειμένου, ή γεγονότος.
Παρόμοιες ικανότητες έχουν και τα βρέφη. Τα πειράματα με βρέφη γίνονται δείχνοντάς τους μια εικόνα με π.χ. δύο αρκουδάκια. Όσο το βρέφος βλέπει εικόνες με δύο αρκουδάκια, συνηθίζει σ’ αυτές και δεν δείχνει κανένα ενδιαφέρον. Μόλις όμως εμφανιστεί εικόνα με τρία αρκουδάκια, το βρέφος στρέφει την προσοχή-του και την παρατηρεί για λίγο διάστημα, λέγοντας ουσιαστικά στον ερευνητή με τον τρόπο αυτόν οτι μπορεί να διακρίνει τη διαφορά του 2 από το 3. Αντίθετα, εικόνα με 6 αρκουδάκια που έρχεται μετά από σειρά εικόνων με 5 δεν προκαλεί την προσοχή του βρέφους, που σημαίνει οτι το βρέφος δεν μπορεί (ακόμα) να διακρίνει τη διαφορά μεταξύ 5 και 6. Η ικανότητα αντίληψης της ποσότητας στον άνθρωπο μεγαλώνει όσο περνούν τα χρόνια, μέχρι την ενηλικίωση.
Έκτος Νόμος: Δημιουργία Συσχετισμών
Ο νόμος αυτός θα μπορούσε να περιγραφεί και σαν πρώτος απ’ όλους, γιατί στην πραγματικότητα εμφανίστηκε χρονολογικά πριν από οποιαδήποτε άλλη “ανώτερη” ή πιο πολύπλοκη νοητική λειτουργία. Πρόκειται για την ικανότητα που έχουν ακόμα και νοητικά εντελώς “πρωτόγονοι” οργανισμοί, όπως θαλάσσια σαλιγκάρια και έντομα, να “μαθαίνουν” πώς να αντιδρούν σε κάποιο εξωτερικό ερέθισμα, ώστε την επόμενη φορά που επαναλαμβάνεται το ερέθισμα ο οργανισμός να αντιδρά διαφορετικά, σαν να έχει “μάθει” κάτι από την προηγούμενη “εμπειρία”.
Προκειμένου για νοητικά απλούστατους οργανισμούς όπως τα σαλιγκάρια, ο μηχανισμός που θα περιγραφεί επιτυγχάνεται μέσω χημικών αλλαγών στις συνδέσεις των νευρώνων του εγκεφάλου, και λέγεται “μάθηση Hebb” (η οποία θα εξεταστεί πιο διεξοδικά στη συνέχεια). Προκειμένου όμως για τον άνθρωπο, ο μηχανισμός αυτός είναι κάτι το πιο γενικό και πιο αφηρημένο, καθώς αναφέρεται σε συνδέσεις εννοιών. Βέβαια, ακόμα και όταν συνδέονται έννοιες, και πάλι έχουμε αλλαγές σε συνδέσεις νευρώνων, σε χαμηλό επίπεδο· πρέπει όμως να αντιληφθούμε οτι σε υψηλό επίπεδο έχουμε μια γενίκευση του μηχανισμού του χαμηλού επιπέδου. Ας δούμε ένα παράδειγμα, για να γίνουν πιο σαφείς οι παρατηρήσεις αυτές.
Ας θεωρήσουμε ένα νήπιο που μαθαίνει τη γλώσσα του περιβάλλοντός του, με τον αυτόματο και υποσυνείδητο τρόπο που μαθαίνει τη γλώσσα το μέσο νήπιο οπουδήποτε στον κόσμο. Το νήπιο βλέπει εικόνες του περιβάλλοντος, και ακούει λέξεις, που πολύ συχνά αναφέρονται ακριβώς σ’ αυτά που βλέπει, ιδιαίτερα όταν του μιλάει κάποιος ενήλικος. Το πρόβλημα που πρέπει να λύσει το νήπιο — πάντα αυτόματα και υποσυνείδητα, κάνοντας χρήση της «γλωσσολογικής-του μηχανής» (βλ. Γ1) — είναι ο συσχετισμός μεταξύ αυτών που βλέπει, και αυτών που ακούει. Η δυσκολία του προβλήματος βρίσκεται στα εξής:
-
Υπάρχει μια πληθώρα οπτικών στοιχείων, δηλαδή πραγμάτων που το νήπιο βλέπει όταν ακούει μια φράση.
-
Επίσης υπάρχει πληθώρα γλωσσικών στοιχείων: λέξεις, που άλλες αντιστοιχούν σε οπτικά σήματα (όπως ρήματα, ουσιαστικά, επίθετα, επιρρήματα, κ.ά.) ενώ άλλες όχι (όπως οι να, θα, και, ή, μορφές του οριστικού άρθρου, και πολλές άλλες). Στα γλωσσικά στοιχεία συγκαταλέγονται και οι καταλήξεις ρημάτων που δηλώνουν αριθμό, πρόσωπο, χρόνο, έγκλιση, και φωνή (τουλάχιστον αυτά ισχύουν στην ελληνική γλώσσα), οι καταλήξεις ουσιαστικών που δηλώνουν αριθμό και ρόλο μέσα στην πρόταση (“πτώση”), κ.ά.
Το νήπιο πρέπει να κάνει τους σωστούς συσχετισμούς ανάμεσα σε όλα αυτά τα στοιχεία. Π.χ. πρέπει να συσχετίσει τη λέξη “κούκλα” με το συγκεκριμένο παιχνίδι που βλέπει, ενώ το “κούκλες” αναφέρεται σε περισσότερα από ένα από αυτά τα αντικείμενα. Συνήθως όμως, κανείς δεν του δίνει μία-μία τις λέξεις και τα γραμματικά “μορφήματα” (βλ. Γ1) που σχετίζονται με έννοιες του περιβάλλοντος. Πώς τα καταφέρνει και κάνει τους σωστούς συσχετισμούς το νήπιο; Δηλαδή πώς ανακαλύπτει το νόημα των όσων ακούει;
Αυτό που θα περιγραφεί στη συνέχεια είναι μια προτεινόμενη λύση του προβλήματος, που υπάρχει στη δημοσίευση Foundalis and Martinez (2007) (*), και που εξηγεί ένα μηχανισμό δημιουργίας συσχετισμών στη γενική-του μορφή (δηλ. όπως μόνο ο άνθρωπος είναι σε θέση να εφαρμόσει).
Ας υποθέσουμε οτι το νήπιο βλέπει εικόνες από ένα βιβλίο κατάλληλο για την ηλικία-του, και οτι κάποιος ενήλικος λέει φράσεις που αντιστοιχούν στις εικόνες αυτές. Για παράδειγμα, μια εικόνα θα μπορούσε να είναι η παρακάτω, ακολουθούμενη από τη φράση του ενήλικου (σε μπλε χρώμα, σε μια υποτιθέμενα άγνωστη γλώσσα):

o sheoil eotzifi ot ipits
Κοιτώντας την εικόνα, το νήπιο μπορεί να δει ορισμένα αντικείμενα (πόρτα, παράθυρο, σκεπή, καπνοδόχο, ολόκληρο το σπίτι, ήλιος, κλπ.), ενώ ακούγοντας τη φράση μπορεί να ξεχωρίσει κάποιες λέξεις (υποθέτουμε οτι έχει φτάσει στο στάδιο όπου μπορεί να ξεχωρίσει λέξεις). Πώς όμως να συσχετίσει αυτά που βλέπει με αυτά που ακούει; Ένας — φαινομενικά απλοϊκός — τρόπος είναι σχηματίζοντας αρχικά όλους τους δυνατούς συσχετισμούς μεταξύ οπτικών στοιχείων και λέξεων, όπως στο επόμενο διάγραμμα:
Στο παραπάνω διάγραμμα, τα οπτικά στοιχεία φαίνονται στο πάνω μέρος, το καθένα σ’ έναν κόκκινο κύκλο. Π.χ. το πρώτο είναι “το σπίτι σαν ολότητα”, και ακολουθούν: “ο ήλιος”, “η σκεπή”, η έννοια “φωτίζει”, “η καπνοδόχος”, και “η πόρτα”. Στην εικόνα υπάρχουν βέβαια κι άλλα, αλλά έστω οτι αυτά είναι όλα κι όλα τα οπτικά στοιχεία που υπέπεσαν στην αντίληψη του νηπίου καθώς κοίταζε την εικόνα. Οι λέξεις που προφέρθηκαν από τον ενήλικο φαίνονται σε μπλε κύκλους ή οβάλ, στο κάτω μέρος. Κάθε λέξη έχει συσχετιστεί με κάθε οπτικό στοιχείο.
Προφανώς οι περισσότεροι από τους συσχετισμούς αυτούς είναι λάθος. Όπως θα δούμε, π.χ. η λέξη “ipits” αντιστοιχεί στο οπτικό στοιχείο “σπίτι” (και ο προσεκτικός αναγνώστης θα μπορέσει να διακρίνει την υποτιθέμενη “γλώσσα” στην οποία είναι γραμμένες οι λέξεις αυτές), επομένως μόνο μία από τις γραμμές-συσχετισμούς που φεύγουν από τη λέξη “ipits” είναι σωστή: αυτή που καταλήγει στο οπτικό στοιχείο “σπίτι σαν ολότητα”, καθώς αυτό εννοεί ο ενήλικος όταν λέει τη λέξη “ipits”. Το νήπιο όμως προς το παρόν δεν το γνωρίζει αυτό, το οποίο πρέπει να “ανακαλύψει”.
Έστω οτι τα παραδείγματα συνεχίζονται με το επόμενο ζευγάρι εικόνας και λέξεων:
o sheoil ot eotzifi samanea poa odu onbau
Βλέπουμε οτι τώρα υπάρχουν ορισμένα διαφορετικά οπτικά στοιχεία, και άλλα που είναι ίδια (π.χ. ο ήλιος). Το ίδιο ισχύει και για τις λέξεις (π.χ. οι τέσσερις πρώτες υπήρχαν και προηγουμένως). Αυτό που μπορεί να κάνει το νήπιο είναι να προσθέσει στη μνήμη-του τα νέα στοιχεία, τόσο τα οπτικά όσο και τα γλωσσικά, όπως στο παρακάτω διάγραμμα, που δείχνει όμως μέρος μόνο των οπτικών και γλωσσικών στοιχείων, λόγω έλλειψης χώρου οριζόντια στην οθόνη:
Στα αρχικά οπτικά στοιχεία έχουν προστεθεί (στο διάγραμμα από αριστερά προς τα δεξιά) τα: “βουνό”, “ανάμεσα”, και “δύο”, όπως και στα γλωσσικά έχουν προστεθεί οι τρεις λέξεις αριστερά.
Το νήπιο μπορεί να κάνει ότι και πριν: να σχηματίσει και πάλι τους συσχετισμούς μεταξύ όλων των λέξεων της καινούριας πρότασης, και όλων των στοιχείων της καινούριας εικόνας (που υπέπεσαν στην αντίληψη του νηπίου), όπως παρακάτω:
Αυτό που βλέπουμε όμως στο παραπάνω διάγραμμα είναι οτι οι δύο συσχετισμοί που προϋπήρχαν (μεταξύ των λέξεων “ot”, “sheoil”, και του οπτικού στοιχείου του ήλιου) ενισχύθηκαν επειδή επαναλήφθηκαν στο δεύτερο παράδειγμα. Αυτό θα το θεωρήσουμε κανόνα του σχηματισμού συσχετισμών (που έχει επαληθευτεί πειραματικά, αλλά σε νοητικά κατώτερους οργανισμούς):
| Συσχετισμοί που
επαναλαμβάνονται, ενισχύονται. Συσχετισμοί που δεν επαναλαμβάνονται, σταδιακά σβήνουν. |
Το δεύτερο σκέλος του παραπάνω κανόνα, δηλαδή το σταδιακό σβήσιμο, αποτυπώνεται στο διάγραμμα με το ελαφρά ανοιχτότερο καφέ χρώμα τόσο των συσχετισμών που δεν επαναλήφθκαν, όσο και των νέων που μόλις προστέθηκαν. Το πόσο γρήγορα ή αργά σβήνουν οι συσχετισμοί είναι μια παράμετρος της διαδικασίας που περιγράφεται. Δίνοντας διαφορετικές τιμές στην παράμετρο αυτή επιτυγχάνουμε ταχύτερη ή πιο αργή εκμάθηση των σωστών συσχετισμών.
Μπορούμε τώρα να φανταστούμε τη διαδικασία αυτή (της παράθεσης εικόνων και φράσεων) να συνεχίζεται. Η μνήμη του νηπίου εμπλουτίζεται με οπτικά και γλωσσικά στοιχεία (αλλά βέβαια στα διαγράμματα που παρουσιάζονται εδώ μπορούμε να δείξουμε μόνο ελάχιστα απ’ αυτά, όσα χωρούν οριζόντια). Το παρακάτω διάγραμμα δείχνει το τί συμβαίνει στους συσχετισμούς καθώς συνεχίζονται τα παραδείγματα: κάποιοι συσχετισμοί ενισχύονται, ενώ κάποιοι άλλοι σταδιακά σβήνουν.
Όταν οι παράμετροι του συστήματος έχουν κατάλληλες τιμές, τότε οι συσχετισμοί που σβήνουν είναι οι λανθασμένοι, γιατί τα λανθασμένα ζευγάρια οπτικών–γλωσσικών στοιχείων δεν επαναλαμβάνονται συχνά (αλλιώς δεν θα ήταν λανθασμένα αλλά σωστά). Τα σωστά ζευγάρια, καθώς επαναλαμβάνονται πότε-πότε, ενισχύουν τους συσχετισμούς-τους. Το τελευταίο “καρέ” του παραπάνω διαγράμματος απεικονίζει την τελική κατάσταση, όπου όλοι οι συσχετισμοί είναι σωστοί εκτός από έναν. (Φυσικά, καθώς το νήπιο ποτέ δεν παύει να δέχεται δεδομένα, και αυτός ο λανθασμένος συσχετισμός τελικά θα σβήσει.) Έτσι το νήπιο μπορεί να μάθει το “νόημα” των λέξεων (και γενικά των γλωσσικών στοιχείων) που ακούει.
Ο βασικός μηχανισμός που επιτρέπει στο σύστημα να δουλεύει σωστά είναι αυτός που περιγράφηκε στο κίτρινο πλαίσιο, παραπάνω. Τίθεται όμως το ερώτημα του πώς υλοποιείται ο μηχανισμός αυτός. Η υλοποίησή του μπορεί να γίνει μέσω μιας μαθηματικής συνάρτησης που λόγω του σχήματός της ονομάζεται “σιγμοειδής” (μοιάζει όμως όχι με κοινό αλλά με τελικό σίγμα):
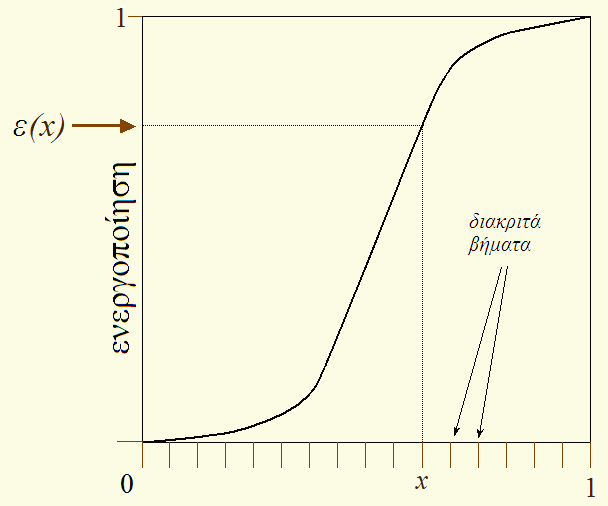
Στον κατακόρυφο άξονα του παραπάνω διαγράμματος είναι ο βαθμός “ενεργοποίησης” του συσχετισμού, δηλαδή το πόσο ισχυρός ή ασθενής είναι ο συσχετισμός: βαθμός ίσος με 1 σημαίνει συσχετισμό εξαιρετικά ισχυρό (όσο πιο ισχυρό γίνεται), ενώ βαθμός ίσος με 0 σημαίνει συσχετισμό που έχει “σβήσει” εντελώς.
Στον οριζόντιο άξονα έχουμε το “πόσες φορές επαναλήφθηκε ο συσχετισμός αυτός”. Παραδείγματος χάρη, αν ο συσχετισμός της λέξης “ipits” με το οπτικό στοιχείο “σπίτι” έχει παρατηρηθεί 10 φορές, τότε κάνουμε 10 βήματα, από αριστερά προς τα δεξιά, πάνω στον οριζόντιο άξονα. (Τα βήματα αυτά λέγονται “διακριτά”, επειδή δεν μετακινούμαστε κατά συνεχή αλλά κατά διακριτό τρόπο πάνω στον άξονα.) Έστω οτι μετά από τα 10 αυτά βήματα βρισκόμαστε στη θέση x του οριζόντιου άξονα. Τότε, για να βρούμε τον βαθμό ενεργοποίησης, φέρουμε από το x μια κατακόρυφη γραμμή προς τα πάνω (όπως στο σχεδιάγραμμα), ώσπου να συναντήσουμε τη σιγμοειδή καμπύλη· στο σημείο της συνάντησης φέρουμε οριζόντια γραμμή προς τ’ αριστερά, οπότε το σημείο που τέμνει η γραμμή αυτή τον κατακόρυφο άξονα είναι ο βαθμός ενεργοποίησης, ε(x), του συσχετισμού.
Κάθε φορά που παρατηρείται ο ίδιος συσχετισμός (π.χ. λέξη “ipits” και εικόνα σπιτιού ταυτόχρονα), το x κάνει ένα βήμα προς τα δεξιά· επομένως ενισχύεται ο βαθμός συσχετισμού, λόγω του σχήματος της σιγμοειδούς καμπύλης που ανεβαίνει προς τα δεξιά. Επίσης όμως, κατά τακτά χρονικά διαστήματα, και εφόσον δεν παρατηρείται ο ίδιος συσχετισμός, το x κάνει ένα βήμα προς τ’ αριστερά, επομένως “πέφτει” ο βαθμός συσχετισμού (και πάλι λόγω του σχήματος της σιγμοειδούς, που κατεβαίνει προς τ’ αριστερά). Το κάθε πότε συμβαίνει η “πτώση” είναι κάτι που καθορίζεται έτσι ώστε το σύστημα να μπορεί να μάθει τους σωστούς συσχετισμούς· δεν πρέπει να συμβαίνει ούτε πολύ συχνά ώστε το σύστημα να ξεχνάει αμέσως τα πάντα, ούτε πολύ σπάνια ώστε το σύστημα να καταλήγει να κάνει όλους τους συσχετισμούς πολύ ισχυρούς (πράγμα που θα σήμαινε οτι θα μάθαινε και όλους τους λανθασμένους συσχετισμούς μαζί με τους σωστούς). Επίσης, και μια άλλη ιδιότητα πρέπει να ισχύει: όσο πιο ισχυρός γίνεται ο συσχετισμός, τόσο πιο σπάνια (λόγω παρέλευσης χρόνου) πρέπει να γίνεται η “πτώση” του συσχετισμού· αν δεν συμβαίνει αυτό, τότε τελικά θα ξεχνιούνται όλοι οι συσχετισμοί μετά από αρκετό χρονικό διάστημα, οπότε το σύστημα θα πάσχει από αμνησία. Σε κάποιες περιπτώσεις, η πτώση πρέπει να είναι τόσο σπάνια ώστε να μη συμβαίνει παρά μόνο μία ή δύο φορές το πολύ στη διάρκεια της ζωής του ατόμου, οπότε ο συσχετισμός αυτός πρέπει να θεωρείται μόνιμος. Τέλος, το πόσα διακριτά βήματα μπορούν να γίνουν πάνω στον οριζόντιο άξονα, είναι κι αυτό μια παράμετρος του συστήματος, δηλαδή μπορεί ν’ αλλάξει προκειμένου να επιτευχθεί το ζητούμενο, που είναι η εκμάθηση των σωστών συσχετισμών.
Εννοείται οτι συσχετισμούς δεν δημιουργούμε μόνο μεταξύ λέξεων και νοημάτων (οπτικών, ακουστικών, αφηρημένων, κλπ), αλλά σε πολλές άλλες περιπτώσεις:
-
Άνθρωποι που ζουν μακριά από μεγαλουπόλεις συνηθίζουν να προβλέπουν τον καιρό της επόμενης μέρας από κάποια σημάδια της προηγούμενης· π.χ.: κόκκινα σύννεφα στη δύση μπορεί να σημαίνουν οτι «αύριο θα βγει αέρας». Αντίστοιχες προγνώσεις κάνουν και οι ναυτικοί. Ανεξάρτητα από το αν οι προγνώσεις αυτές είναι σωστές ή όχι, οι “κανόνες” έχουν δημιουργηθεί μέσω εμπειρικών συσχετισμών (π.χ., κόκκινα σύννεφα τη μια μέρα, δυνατός αέρας την επόμενη, κλπ).
-
Η εκτέλεση μιας μαγειρικής συνταγής μπορεί κάποια φορά να έχει ιδιαίτερη επιτυχία ή αποτυχία. Όταν συμβεί αυτό, μπορεί να προσπαθήσουμε να βρούμε τί ήταν αυτό που αλλάξαμε (από το συνηθισμένο τρόπο εκτέλεσής της) και που μας οδήγησε στην επιτυχία ή αποτυχία. Θα κάνουμε επομένως ένα συσχετισμό μεταξύ διαφορετικού υλικού (ή διαδικασίας) και αποτελέσματος.
-
Αν έχουμε συνηθίσει να βλέπουμε δύο φίλους (ή ένα ανδρόγυνο) σχεδόν πάντα μαζί, τότε βλέποντας μόνο το ένα άτομο μια μέρα θα αναρωτηθούμε (και μπορεί να ρωτήσουμε) πώς είναι το άλλο άτομο, που συσχετίζουμε με το πρώτο.
Το τελευταίο παράδειγμα θυμίζει έντονα τον Τρίτο Νόμο: τη συμπλήρωση μοτίβου, γιατί όταν θυμόμαστε το ένα άτομο μέσω του άλλου δεν κάνουμε τίποτα άλλο από το να προβλέπουμε το όλο βάσει του μέρους. Πράγματι, για να υλοποιηθεί ο Τρίτος Νόμος απαιτείται τουλάχιστον η ικανότητα δημιουργίας συσχετισμών μέσω του Έκτου Νόμου, κάτι όμως που μπορεί να αναφερθεί μόλις τώρα, εφόσον έχουμε γνωρίσει τα σχετικά με τον Έκτο Νόμο.
Όπως αναφέρθηκε στην αρχή αυτής της υπο-ενότητας, την ικανότητα δημιουργίας συσχετισμών την έχουν και τα ζώα. Ας δούμε ένα χαρακτηριστικό (και πραγματικό) παράδειγμα. Επισκέπτης του “Αττικού Ζωολογικού Πάρκου” στα Σπάτα παρατήρησε οτι σε ένα πουλί “κακατού” (συγγενικό των παπαγάλων) άρεζε να πλησιάζει τη σιδερένια σίτα του χώρου όπου βρισκόταν και να αφήνει να το χαϊδεύουν οι επισκέπτες, με το δάχτυλο στο λαιμό και κάτω από τη φτερούγα. Πράγματι, ο επισκέπτης πλησίασε και το χάιδεψε για λίγη ώρα. Όταν όμως έκανε να φύγει, άκουσε το πουλί να του λέει: «Τί κάνεις;» (Τα κακατού είναι από τα είδη που μπορούν να μάθουν να “μιλούν”, μερικά μάλιστα είναι ομιλιτικότατα.) Ο επισκέπτης εντυπωσιάστηκε, πλησίασε το κλουβί, και το χάιδεψε λίγο ακόμα, μιλώντας-του και προσπαθώντας να το κάνει να μιλήσει πάλι, αλλά χωρίς επιτυχία. Όταν έκανε να απομακρυνθεί όμως, το κακατού είπε και πάλι: «Τί κάνεις;» Αυτή τη φορά ο επισκέπτης “έπιασε” το νόημα: κάθε φορά που απομακρυνόταν από το κλουβί, το κακατού έλεγε «Τί κάνεις;», ωθώντας τον επισκέπτη να το ξαναπλησιάσει και να το χαϊδέψει. Ο επισκέπτης τότε ζήτησε από ένα φιλικό άτομο που τον συνόδευε να χαϊδέψει το κακατού, μέχρι που και οι δυο-τους απομακρύνθηκαν ταυτόχρονα, κάνοντας το πουλί να επαναλάβει τη γνωστή φράση, ενώ ο επισκέπτης τράβηξε τη σκηνή αυτή σε βίντεο, που το βλέπουμε παρακάτω:
Εδώ έχουμε τη δημιουργία δύο συσχετισμών: έναν εκ μέρους του ανθρώπου, και έναν εκ μέρους του πτηνού. Κατ’ αρχήν ο άνθρωπος χρειάστηκε δύο επαναλήψεις για να καταλάβει το συσχετισμό: «Η απομάκρυνσή μου από το κλουβί συνδέεται με το οτι το κακατού λέει: “Τί κάνεις;”.» Όμως η κατανόηση του συσχετισμού από τον άνθρωπο είναι αναμενόμενη και κάθε άλλο παρά εντυπωσιακή. Αυτό που είναι εντυπωσιακό είναι η αντίληψη ενός άλλου συσχετισμού από το κακατού. Προφανώς το πτηνό αυτό κάποτε έμαθε (ή του έμαθαν) να λέει: «Τί κάνεις;»· επίσης του άρεζε να το χαϊδεύουν. Κάποτε, όταν ένας επισκέπτης σταμάτησε να το χαϊδεύει και απομακρύνθηκε από το κλουβί, το κακατού αντέδρασε με όποιον τρόπο θα μπορούσε να αντιδράσει στο “δυσάρεστο” γεγονός της απομάκρυνσης, και μία από τις αντιδράσεις-του ήταν το να πει αυτό που είχε μάθει, δηλ. «Τί κάνεις;». Ο αρχικός εκείνος επισκέπτης, όπως και εκείνος του παραπάνω βίντεο, επέστρεψε στο κλουβί και χάιδεψε λίγο ακόμη το πτηνό. Το κακατού λοιπόν κατάφερε να κάνει το συσχετισμό: “εκφορά του «Τί κάνεις;» → περισσότερο χάιδεμα”. Για όσους εργάζονται στον τομέα της ζωικής ψυχολογίας (αγγλ.: animal psychology) αυτό το κατόρθωμα δεν είναι καθόλου παράξενο ή απροσδόκητο. Για τους υπόλοιπους όμως, δίνει μια ιδέα για τις δυνατότητες της ζωικής νοημοσύνης.
Σημειώσεις:
(^) Η ίδια παρατήρηση ισχύει και για τις έννοιες. Είναι οι έννοιες υλικές ή όχι; Αν αναλύσουμε τον τρόπο με τον οποίο υλοποιείται μια έννοια μέσω νευρώνων του εγκεφάλου θα δούμε οτι πράγματι υπάρχει ένας μεγάλος αριθμός νευρώνων (πολύ μεγάλος, της τάξης των εκατοντάδων εκατομμυρίων ή και δισεκατομμυρίων, εξαρτώμενος από την πολυπλοκότητα της έννοιας) που συμμετέχουν στην υλοποίησή της. Εντούτοις: (α) δεν πρόκειται για ένα συγκεκριμένο σύνολο νευρώνων που υλοποιούν την υπό εξέταση έννοια, καθώς η κατανομή της έννοιας στους νευρώνες αλλάζει από μέρα σε μέρα και από ώρα σε ώρα· (β) οι ίδιοι νευρώνες ασχολούνται με την υλοποίηση πολλών άλλων εννοιών· και (γ) δεν υπάρχουν σαφή όρια μέσα στον εγκέφαλο ώστε να μπορούμε να πούμε οτι αυτοί οι νευρώνες (και όχι άλλοι) αυτή τη στιγμή υλοποιούν την έννοια, καθώς οι έννοιες καθαυτό δεν έχουν σαφή όρια, όπως θα μάθουμε αργότερα στο μάθημα. Επομένως, ναι μεν οι έννοιες τελικά έχουν φυσική υπόσταση σ’ έναν εγκέφαλο, αλλά δεν μπορούμε να τις “δείξουμε” (ακόμα κι αν διαθέταμε την τεχνογνωσία και τα τεχνικά μέσα) με τον ίδιο τρόπο που δείχνουμε ένα τραπέζι ή ένα βιβλίο. Τόσο το “αντικείμενο τραπέζι” όσο και η “έννοια τραπέζι” είναι τελικά υλικά αντικείμενα· όμως το αντικείμενο τραπέζι αποτελείται από μόρια ύλης με τόσο σαφή όρια που μπορούμε να το πιάσουμε και να το μετακινήσουμε· αντίθετα, η υλική υπόσταση της έννοιας “τραπέζι”, στα βάθη ενός εγκεφάλου, είναι τόσο ακαθόριστη (καί στο χώρο καί στο χρόνο) που δεν έχει νόημα να τη θεωρούμε σαν υλικό αντικείμενο με τη στενή έννοια (σαν κάτι το ορατό, απτό, κλπ.). Πιο χρήσιμο και παραγωγικό είναι να θεωρούμε τις έννοιες σαν αφηρημένες οντότητες που υπόκεινται σε νόμους και διαδικασίες που περιγράφονται στο παρόν μάθημα.
(^) Γραμματική Αχιλλέως Τζαρτζάνου, Εκδ. Καλοκάθη, σελ. 38.
(^) Η άρνηση είναι μια από τις απλούστερες και στοιχειώδεις συντακτικές δομές. Υπάρχουν πάμπολλες άλλες, τόσο στοιχειώδεις όσο και σύνθετες. Κάθε πλήρης πρόταση, για παράδειγμα, όπως η «Ο δρόμος καθαρίστηκε προχθές από τους εργάτες του δήμου» είναι μια (σύνθετη) συντακτική δομή, όχι έννοια· το ίδιο ισχύει και για μια “προθετική φράση”, όπως την «Με τις καλύτερες ευχές»· κλπ.
(^) Νά τί σημαίνει ο 3ος τύπος του ΓΜΠ. Ο αριθμητής σημαίνει το εξής: άθροισε τις ομοιότητες της δοσμένης κουκκίδας i με τις κουκκίδες που ανήκουν στην κατηγορία J της οποίας ζητάμε να βρούμε την πιθανότητα να της ανήκει η κουκκίδα i. Και ο παρονομαστής του κλάσματος σημαίνει το εξής: άθροισε τις ομοιότητες της δοσμένης κουκκίδας i με όλες τις κουκκίδες που έχεις δει μέχρι στιγμής (όλων των κατηγοριών). Διαιρούμε αριθμητή δια παρονομαστή, και το κλάσμα μας δίνει την πιθανότητα να ανήκει η κουκκίδα i στην κατηγορία J.
(^) Αλλά εκτελούνται κατά δισεκατομμύρια ανά δευτερόλεπτο. Δηλαδή, οι υπολογιστές κάνουν αστρονομικά περισσότερες πράξεις από ένα νευρώνα ανά μονάδα χρόνου, αλλά τις πράξεις αυτές τις κάνουν ακολουθιακά, μία-μία· ενώ σε έναν εγκέφαλο, ο ένας νευρώνας μπορεί να είναι απελπιστικά αργός σε σχέση με τον υπολογιστή, αλλά δισεκατομμύρια νευρώνες δουλεύουν παράλληλα. Αυτό έχει σαν αποτέλεσμα κάποια προβλήματα που λύνονται γρήγορα από τον εγκέφαλο να απαιτούν πολύ περισσότερο χρόνο από τον υπολογιστή, και αντιστρόφως.
(^) Για να δημιουργήσουμε μια νέα κατηγορία μέσω του ΓΜΠ θα πρέπει να εισάγουμε μια επιπλέον παράμετρο: ένα “κατώφλι” πιθανότητας, έτσι ώστε όταν η τιμή της πιθανότητας που παράγει ο 3ος τύπος είναι μικρότερη από αυτό το κατώφλι, να συμπεραίνουμε οτι το δοσμένο είδος πρέπει να δημιουργήσει (και να τοποθετηθεί σε) μια νέα κατηγορία.
(^) Ιδού ο 3ος τύπος βάσει της θεωρίας προτύπου:
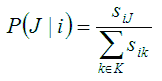
Εδώ ο αριθμητής SiJ είναι η ομοιότητα του δοσμένου είδους i με το πρότυπο της κατηγορίας J. Ο παρονομαστής είναι το άθροισμα των ομοιοτήτων του είδους i με τα πρότυπα k όλων των μέχρι τώρα γνωστών κατηγοριών Κ (φυσικά περιλαμβανομένης και της κατηγορίας J ).
(^) [Σ.τ.Μ.:] Στον πατέρα-του, Robert Hofstadter, απονεμήθηκε το Νόμπελ φυσικής το 1961.
(^) Η ενοποίηση (unification) του 1ου και 2ου Νόμου περιγράφεται σ’ αυτήν τη δημοσίευση (pdf, στα αγγλικά).
(^) Δηλαδή η πρόβλεψη δεν είναι ένας απλός αριθμός, αλλά ένα εύρος τιμών, συνοδευόμενο από μια πιθανότητα ώστε η αναμενόμενη τιμή να ανήκει στο εύρος αυτό των τιμών.
(^) Ας μην ξεχνάμε οτι από την προσπάθεια να ελαχιστοποιηθούν τα πέντε αιτήματα (αξιώματα) του Ευκλείδη (δηλαδή να αποδειχτεί το 5ο αίτημα βάσει των υπόλοιπων τεσσάρων) αναπτύχθηκαν οι μη-Ευκλείδειες γεωμετρίες, που έπαιξαν σπουδαίο ρόλο τον 20ό αιώνα στη θεωρία της σχετικότητας. (Βλ. μάθημα Ε2.) Η πίστη στην εγκυρότητα του ξυραφιού του Όκαμ είναι υπεύθυνη ακόμα και για όψεις της καθημερινότητάς μας.
(^) Τα εικονιζόμενα είναι τα Κυκλαδίτικα νησιά Άνδρος (αριστερά), και Νάξος (δεξιά). Λίγη γνώση ελληνικής γεωγραφίας μας λέει οτι η Νάξος είναι το μεγαλύτερο νησί των Κυκλάδων, ενώ η Άνδρος είναι το δεύτερο μεγαλύτερο νησί της ίδιας Αιγαιοπελαγίτικης ομάδας. Εδώ υποθέτουμε οτι δεν έχουμε τη γνώση αυτή, ώστε να συμπεράνουμε με το “μάτι” (και όχι λόγω γνώσης) οτι το νησί στα δεξιά (Νάξος) είναι μεγαλύτερο.
(^) Στο διάγραμμα, το νησί στ’ αριστερά (Άνδρος) έχει 101 κουκκίδες, ενώ εκείνο στα δεξιά (Νάξος) 116 κουκκίδες, δηλ. έχουν λόγο: 101 / 116 = 0.87. Στην πραγματικότητα η Άνδρος έχει επιφάνεια 374 χλμ2, ενώ η Νάξος 428 χλμ2, δηλαδή και πάλι ο λόγος των επιφανειών-τους είναι: 374 / 428 = 0.87. Άρα και μέσω των κουκκίδων μπορούμε να προσεγγίσουμε ικανοποιητικά το πρόβλημα της σύγκρισης εμβαδών.
(^) Πώς συμβαίνει να καταφέρνουν τυχαία κάτι τέτοιο οι αρουραίοι; Γίνεται γιατί τα ζώα αυτά, σε συνθήκες πίεσης για ανεύρεση τροφής (ή αποφυγής κινδύνου, κλπ.), δοκιμάζουν ότι είναι δυνατό να γίνει στο περιβάλλον-τους, με τυχαίο τρόπο. Κάποια στιγμή απλά τυχαίνει να πατήσουν το σωστό αριθμό φορών τους μοχλούς Α και Β, οπότε όταν ανοίγει η δίοδος σημειώνουν τη συσχέτιση μεταξύ μοχλών και τροφής, μέσω μηχανισμού που θα περιγραφεί στον Έκτο Νόμο. Την επόμενη φορά που θα βρεθούν στο ίδιο περιβάλλον, θα είναι πιο συγκεντρωμένοι στα χτυπήματα των μοχλών (δεν θα χάσουν πολύ χρόνο π.χ. προσπαθώντας να ανεβούν στα τοιχώματα), οπότε θα φτάσουν πιο γρήγορα στη λύση· την τρίτη φορά θα τα καταφέρουν ακόμα πιο γρήγορα, κ.ο.κ.
(^) Foundalis, Harry E. and M. Martínez (2007). “A Generalization of Hebbian Learning in Perceptual and Conceptual Categorization” («Μια γενίκευση της εκμάθησης Hebb στην αντιληπτική και εννοιολογική κατηγοριοποίηση»). Στο: Πρακτικά του Ευρωπαϊκού Συνεδρίου Νοολογίας, Δελφοί, Ελλάδα, Μάιος 2007, σελ. 312–317. (Κατεβάστε-το, pdf στα αγγλικά.)
Πίσω στη γενική σελίδα του Διαδικτυακού Επιστημονικού Πανεπιστημίου